17.2 直角三角形 同步练(含答案) 2025-2026学年数学冀教版(2024)八年级上册
文档属性
| 名称 | 17.2 直角三角形 同步练(含答案) 2025-2026学年数学冀教版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 151.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 23:23:07 | ||
图片预览


文档简介
17.2直角三角形
直角三角形两个锐角互余的性质与直角三角形的判定
1.在Rt△ABC中,∠C=90°,∠B=40°,则∠A= ( )
A.60° B.30° C.50° D.40°
2.在△ABC中,下列条件:①∠A+∠B=90°;②∠A=40°,∠B=50°;③∠A∶∠B∶∠C=1∶2∶3;
④∠A=5∠B.其中,能判定△ABC是直角三角形的是 (填序号).
直角三角形斜边上的中线的性质
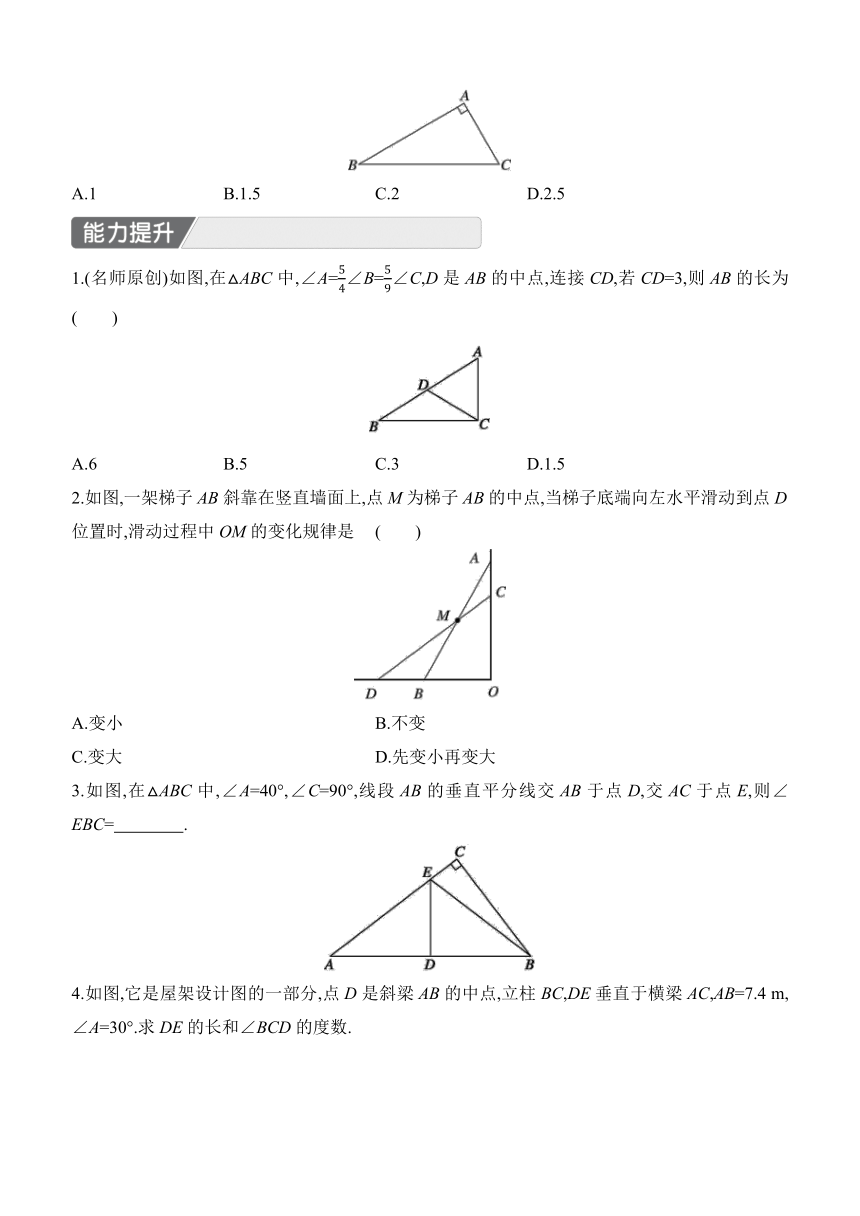
3.如图,在Rt△ABC中,CD是斜边AB上的中线,∠A=20°,则∠BCD的度数是 ( )
A.40° B.50°
C.60° D.70°
4.如图,在△ABC中,∠ACB=90°,∠B=55°,D是斜边AB的中点,那么∠ACD的度数为 ( )
A.15° B.25°
C.35° D.45°
5.如图,在△ABC中,D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
含30 °角的直角三角形的性质
6.如图,在△ABC中,∠A=90°,∠C=60°,BC=4,则AC的长为 ( )
A.1 B.1.5 C.2 D.2.5
1.(名师原创)如图,在△ABC中,∠A=∠B=∠C,D是AB的中点,连接CD,若CD=3,则AB的长为( )
A.6 B.5 C.3 D.1.5
2.如图,一架梯子AB斜靠在竖直墙面上,点M为梯子AB的中点,当梯子底端向左水平滑动到点D位置时,滑动过程中OM的变化规律是 ( )
A.变小 B.不变
C.变大 D.先变小再变大
3.如图,在△ABC中,∠A=40°,∠C=90°,线段AB的垂直平分线交AB于点D,交AC于点E,则∠EBC= .
4.如图,它是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=7.4 m,∠A=30°.求DE的长和∠BCD的度数.
5.如图,在△ABC中,AD是中线,∠ABC=∠ACB,CE⊥AB于点E,交AD于点O,F是AC的中点,连接EF,DE,DF.
(1)若∠B=67°,求∠BAD的度数.
(2)求证:直线DF垂直平分CE.
(3)若∠BAC=45°,AO=a,AB=b,直接写出△DEF的周长(用含有a,b的代数式表示).
微专题7 构造含30°角的直角三角形的常用技巧
含30°角的直角三角形是一个重要的数学模型,常用于线段的计算或证明一条线段是另一条线段的2倍,所以当图中没有含30°角的直角三角形时,常通过作辅助线构造该图形,而作辅助线的技巧主要是连接、作垂线或延长等.
1.如图,在△ABC中,AB=AC,∠C=30°,点D是AB的中点,过点D作DE⊥AB交BC于点E,DE=2,则CE的长度为 ( )
A.7 B.8 C.9 D.10
2.小亮想测量某池塘的宽度,他结合所学的数学知识并考虑到地形条件,设计了如图所示的测量方案:先在池塘外的空地上任取一点O,连接AO,CO,并延长CO至点D,使OC=
OD,过点D作AC的平行线DE,延长AO至点F,连接EF,测得∠DEF=120°,∠OFE=90°,DE=
5 m,EF=9 m,请求出池塘宽度AC.
【详解答案】
基础达标
1.C 2.①②③ 3.D 4.C 5.1
6.C
能力提升
1.A 解析:∵∠B=∠A,∠C=∠A,∠A+∠B+∠C=180°,∴∠A+∠A+∠A=180°,解得∠A=50°,∴∠B=40°,
∴△ABC是直角三角形,且AB是斜边,∵D是AB的中点,∴AB=2CD=2×3=6.故选A.
2.B 解析:∵∠AOB=90°,M为AB的中点,∴OM=AB.同理,OM=CD.∵AB=CD,∴OM的长度不变.故选B.
3.10° 解析:∵∠C=90°,∠A=40°,∴∠ABC=90°-∠A=50°.∵DE是线段AB的垂直平分线,∴AE=BE.
∴∠EBA=∠A=40°.∴∠EBC=∠ABC-∠EBA=50°-40°=10°.
4.解:∵DE⊥AC,BC⊥AC,∠A=30°,
∴BC=AB=BD=×7.4=3.7(m).
又AD=AB=3.7 m,
∴DE=AD=1.85 m.
在Rt△ACB中,∠ABC=60°,
又BC=BD,
∴△BCD是等边三角形,
∴∠BCD=60°.
答:立柱DE的长是1.85 m.∠BCD=60°.
5.解:(1)∵∠ABC=∠ACB,
∴AB=AC.
∵AD是△ABC的中线,
∴AD⊥BC.
∴∠B+∠BAD=90°.
∵∠B=67°,
∴∠BAD=90°-67°=23°.
(2)证明:∵F是AC的中点,
∴CF=AC.
∵CE⊥AB,
∴∠AEC=∠BEC=90°.
∴EF=AC.
∴EF=CF.
∴点F在CE的垂直平分线上.
∵D是BC的中点,
∴CD=ED=BC.
∴点D在CE的垂直平分线上.
∴直线DF垂直平分CE.
(3)△DEF的周长为a+b.
解析:∵∠AEC=90°,∠BAC=45°,AC=AB=b,F是AC的中点,
∴EF=AF=FC=,AE=EC.
∵∠ADC=90°,F是AC的中点,
∴DF=AC=.
∵∠B+∠BAD=90°=∠B+∠BCE,
∴∠BAD=∠BCE.
在△AEO和△CEB中,
∴△AEO≌△CEB(ASA).
∴AO=BC=a.
∵∠CEB=90°,BD=CD,
∴ED=BC=.
∴△DEF的周长=EF+DF+ED=a+b.
微专题7
1.B 解析:连接AE,如图,∵AB=AC,∴∠B=∠C=30°,则∠BAC=180°-(∠B+∠C)=120°,∵点D是AB的中点,DE⊥AB,∴DE是线段AB的垂直平分线,∴BE=AE,∴∠B=∠DAE=30°,在Rt△ADE中,AE=2DE=4,∵∠BAC=120°,
∠DAE=30°,∴∠CAE=∠BAC-∠DAE=120°-30°=90°,在Rt△CAE中,∠C=30°,AE=4,∴CE=2AE=8.故选B.
2.解:延长DE,AF交于点B,如图所示.
∵DE∥AC,
∴∠C=∠D,
在△OAC和△OBD中,
∴△OAC≌△OBD(ASA).
∴AC=BD,
∵∠DEF=120°,∠OFE=90°,
∴∠BFE=90°,∠BEF=60°,
∴∠B=30°,
∵EF=9 m,
∴BE=2EF=18 m,
∵DE=5 m,
∴BD=BE+DE=23 m,
∴AC=23 m.
答:池塘宽度AC为23 m.
直角三角形两个锐角互余的性质与直角三角形的判定
1.在Rt△ABC中,∠C=90°,∠B=40°,则∠A= ( )
A.60° B.30° C.50° D.40°
2.在△ABC中,下列条件:①∠A+∠B=90°;②∠A=40°,∠B=50°;③∠A∶∠B∶∠C=1∶2∶3;
④∠A=5∠B.其中,能判定△ABC是直角三角形的是 (填序号).
直角三角形斜边上的中线的性质
3.如图,在Rt△ABC中,CD是斜边AB上的中线,∠A=20°,则∠BCD的度数是 ( )
A.40° B.50°
C.60° D.70°
4.如图,在△ABC中,∠ACB=90°,∠B=55°,D是斜边AB的中点,那么∠ACD的度数为 ( )
A.15° B.25°
C.35° D.45°
5.如图,在△ABC中,D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
含30 °角的直角三角形的性质
6.如图,在△ABC中,∠A=90°,∠C=60°,BC=4,则AC的长为 ( )
A.1 B.1.5 C.2 D.2.5
1.(名师原创)如图,在△ABC中,∠A=∠B=∠C,D是AB的中点,连接CD,若CD=3,则AB的长为( )
A.6 B.5 C.3 D.1.5
2.如图,一架梯子AB斜靠在竖直墙面上,点M为梯子AB的中点,当梯子底端向左水平滑动到点D位置时,滑动过程中OM的变化规律是 ( )
A.变小 B.不变
C.变大 D.先变小再变大
3.如图,在△ABC中,∠A=40°,∠C=90°,线段AB的垂直平分线交AB于点D,交AC于点E,则∠EBC= .
4.如图,它是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=7.4 m,∠A=30°.求DE的长和∠BCD的度数.
5.如图,在△ABC中,AD是中线,∠ABC=∠ACB,CE⊥AB于点E,交AD于点O,F是AC的中点,连接EF,DE,DF.
(1)若∠B=67°,求∠BAD的度数.
(2)求证:直线DF垂直平分CE.
(3)若∠BAC=45°,AO=a,AB=b,直接写出△DEF的周长(用含有a,b的代数式表示).
微专题7 构造含30°角的直角三角形的常用技巧
含30°角的直角三角形是一个重要的数学模型,常用于线段的计算或证明一条线段是另一条线段的2倍,所以当图中没有含30°角的直角三角形时,常通过作辅助线构造该图形,而作辅助线的技巧主要是连接、作垂线或延长等.
1.如图,在△ABC中,AB=AC,∠C=30°,点D是AB的中点,过点D作DE⊥AB交BC于点E,DE=2,则CE的长度为 ( )
A.7 B.8 C.9 D.10
2.小亮想测量某池塘的宽度,他结合所学的数学知识并考虑到地形条件,设计了如图所示的测量方案:先在池塘外的空地上任取一点O,连接AO,CO,并延长CO至点D,使OC=
OD,过点D作AC的平行线DE,延长AO至点F,连接EF,测得∠DEF=120°,∠OFE=90°,DE=
5 m,EF=9 m,请求出池塘宽度AC.
【详解答案】
基础达标
1.C 2.①②③ 3.D 4.C 5.1
6.C
能力提升
1.A 解析:∵∠B=∠A,∠C=∠A,∠A+∠B+∠C=180°,∴∠A+∠A+∠A=180°,解得∠A=50°,∴∠B=40°,
∴△ABC是直角三角形,且AB是斜边,∵D是AB的中点,∴AB=2CD=2×3=6.故选A.
2.B 解析:∵∠AOB=90°,M为AB的中点,∴OM=AB.同理,OM=CD.∵AB=CD,∴OM的长度不变.故选B.
3.10° 解析:∵∠C=90°,∠A=40°,∴∠ABC=90°-∠A=50°.∵DE是线段AB的垂直平分线,∴AE=BE.
∴∠EBA=∠A=40°.∴∠EBC=∠ABC-∠EBA=50°-40°=10°.
4.解:∵DE⊥AC,BC⊥AC,∠A=30°,
∴BC=AB=BD=×7.4=3.7(m).
又AD=AB=3.7 m,
∴DE=AD=1.85 m.
在Rt△ACB中,∠ABC=60°,
又BC=BD,
∴△BCD是等边三角形,
∴∠BCD=60°.
答:立柱DE的长是1.85 m.∠BCD=60°.
5.解:(1)∵∠ABC=∠ACB,
∴AB=AC.
∵AD是△ABC的中线,
∴AD⊥BC.
∴∠B+∠BAD=90°.
∵∠B=67°,
∴∠BAD=90°-67°=23°.
(2)证明:∵F是AC的中点,
∴CF=AC.
∵CE⊥AB,
∴∠AEC=∠BEC=90°.
∴EF=AC.
∴EF=CF.
∴点F在CE的垂直平分线上.
∵D是BC的中点,
∴CD=ED=BC.
∴点D在CE的垂直平分线上.
∴直线DF垂直平分CE.
(3)△DEF的周长为a+b.
解析:∵∠AEC=90°,∠BAC=45°,AC=AB=b,F是AC的中点,
∴EF=AF=FC=,AE=EC.
∵∠ADC=90°,F是AC的中点,
∴DF=AC=.
∵∠B+∠BAD=90°=∠B+∠BCE,
∴∠BAD=∠BCE.
在△AEO和△CEB中,
∴△AEO≌△CEB(ASA).
∴AO=BC=a.
∵∠CEB=90°,BD=CD,
∴ED=BC=.
∴△DEF的周长=EF+DF+ED=a+b.
微专题7
1.B 解析:连接AE,如图,∵AB=AC,∴∠B=∠C=30°,则∠BAC=180°-(∠B+∠C)=120°,∵点D是AB的中点,DE⊥AB,∴DE是线段AB的垂直平分线,∴BE=AE,∴∠B=∠DAE=30°,在Rt△ADE中,AE=2DE=4,∵∠BAC=120°,
∠DAE=30°,∴∠CAE=∠BAC-∠DAE=120°-30°=90°,在Rt△CAE中,∠C=30°,AE=4,∴CE=2AE=8.故选B.
2.解:延长DE,AF交于点B,如图所示.
∵DE∥AC,
∴∠C=∠D,
在△OAC和△OBD中,
∴△OAC≌△OBD(ASA).
∴AC=BD,
∵∠DEF=120°,∠OFE=90°,
∴∠BFE=90°,∠BEF=60°,
∴∠B=30°,
∵EF=9 m,
∴BE=2EF=18 m,
∵DE=5 m,
∴BD=BE+DE=23 m,
∴AC=23 m.
答:池塘宽度AC为23 m.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
