第十六章 轴对称和中心对称 测试卷(含答案) 2025-2026学年数学冀教版(2024)八年级上册
文档属性
| 名称 | 第十六章 轴对称和中心对称 测试卷(含答案) 2025-2026学年数学冀教版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 250.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 13:32:17 | ||
图片预览


文档简介
第十六章 轴对称和中心对称 测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
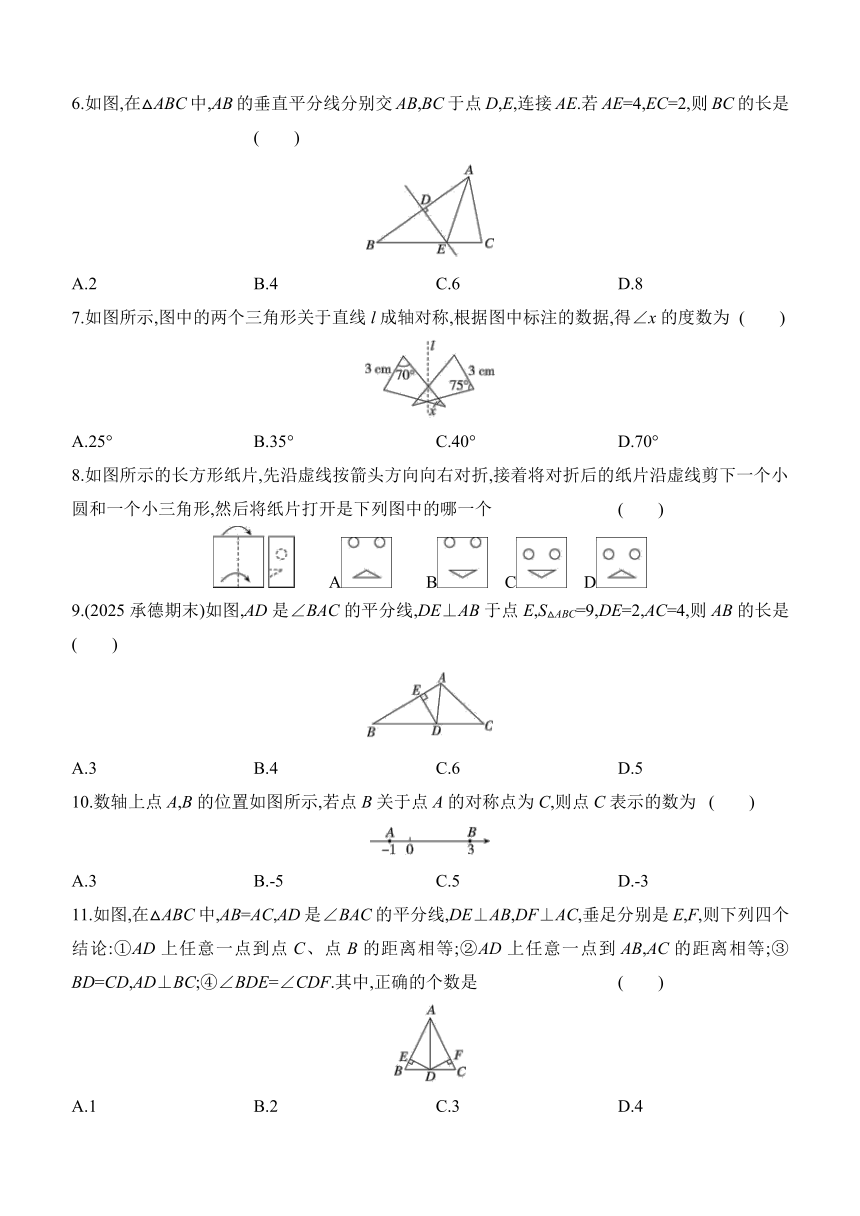
1.(2024淄博中考)下列图案中,既是轴对称图形又是中心对称图形的是 ( )
A B C D
2.如图所示的图案是由六个全等的菱形(各边相等的四边形)拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的是 ( )
A B C D
3.如图是一个由六个正方形组成的网格.现在嘉嘉想再涂上一个正方形,使四个阴影正方形所组成的图形是中心对称图形,则嘉嘉应该涂 ( )
A.①或② B.②
C.②或③ D.③
4.下列说法中,正确的是 ( )
A.两个全等的三角形一定关于某条直线对称
B.两个图形关于某条直线对称,对应点一定在直线两旁
C.成轴对称的两个图形的对应点连线的垂线,就是它们的对称轴
D.关于某条直线对称的两个三角形是全等三角形
5.如图,是小亮在某时刻从镜子里看到镜子对面电子钟的像,则这个时刻是 ( )
A.10:21 B.10:51
C.21:10 D.15:01
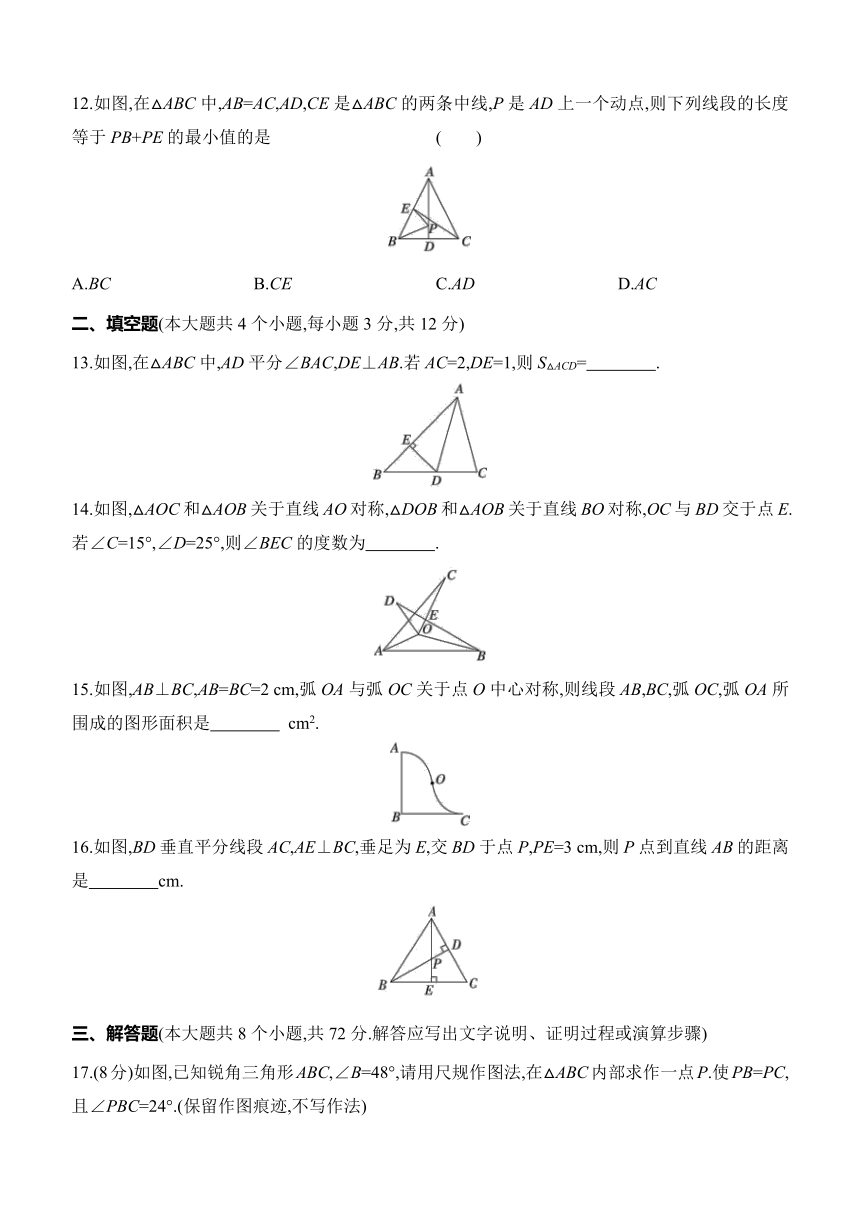
6.如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,连接AE.若AE=4,EC=2,则BC的长是 ( )
A.2 B.4 C.6 D.8
7.如图所示,图中的两个三角形关于直线l成轴对称,根据图中标注的数据,得∠x的度数为 ( )
A.25° B.35° C.40° D.70°
8.如图所示的长方形纸片,先沿虚线按箭头方向向右对折,接着将对折后的纸片沿虚线剪下一个小圆和一个小三角形,然后将纸片打开是下列图中的哪一个 ( )
A B C D
9.(2025承德期末)如图,AD是∠BAC的平分线,DE⊥AB于点E,S△ABC=9,DE=2,AC=4,则AB的长是( )
A.3 B.4 C.6 D.5
10.数轴上点A,B的位置如图所示,若点B关于点A的对称点为C,则点C表示的数为 ( )
A.3 B.-5 C.5 D.-3
11.如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,则下列四个结论:①AD上任意一点到点C、点B的距离相等;②AD上任意一点到AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.其中,正确的个数是 ( )
A.1 B.2 C.3 D.4
12.如图,在△ABC中,AB=AC,AD,CE是△ABC的两条中线,P是AD上一个动点,则下列线段的长度等于PB+PE的最小值的是 ( )
A.BC B.CE C.AD D.AC
二、填空题(本大题共4个小题,每小题3分,共12分)
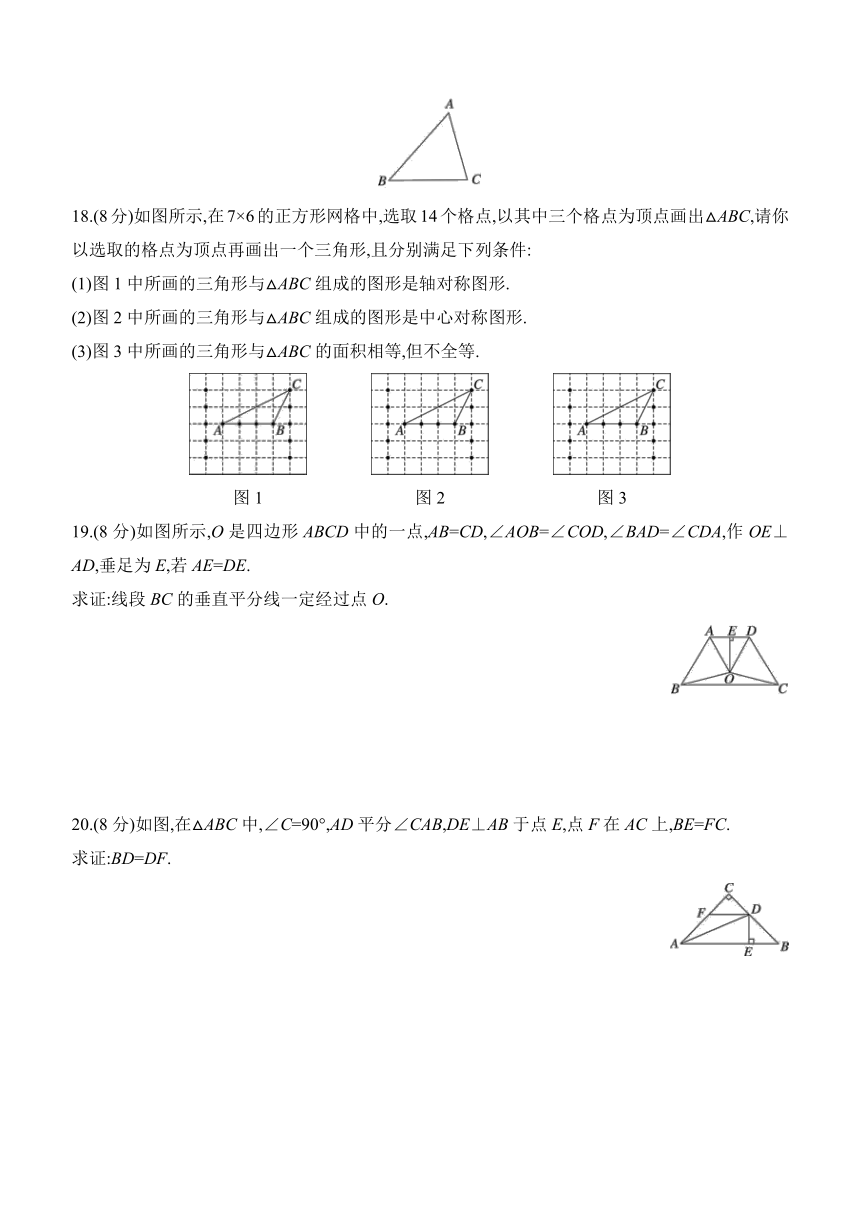
13.如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= .
14.如图,△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,OC与BD交于点E.若∠C=15°,∠D=25°,则∠BEC的度数为 .
15.如图,AB⊥BC,AB=BC=2 cm,弧OA与弧OC关于点O中心对称,则线段AB,BC,弧OC,弧OA所围成的图形面积是 cm2.
16.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于点P,PE=3 cm,则P点到直线AB的距离是 cm.
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)如图,已知锐角三角形ABC,∠B=48°,请用尺规作图法,在△ABC内部求作一点P.使PB=PC,且∠PBC=24°.(保留作图痕迹,不写作法)
18.(8分)如图所示,在7×6的正方形网格中,选取14个格点,以其中三个格点为顶点画出△ABC,请你以选取的格点为顶点再画出一个三角形,且分别满足下列条件:
(1)图1中所画的三角形与△ABC组成的图形是轴对称图形.
(2)图2中所画的三角形与△ABC组成的图形是中心对称图形.
(3)图3中所画的三角形与△ABC的面积相等,但不全等.
图1 图2 图3
19.(8分)如图所示,O是四边形ABCD中的一点,AB=CD,∠AOB=∠COD,∠BAD=∠CDA,作OE⊥AD,垂足为E,若AE=DE.
求证:线段BC的垂直平分线一定经过点O.
20.(8分)如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.
求证:BD=DF.
21.(8分)如图所示,在长方形硬纸片的右下角画有一个圆,小丽想把这张硬纸片剪成两块,使两块硬纸片的面积相等,并且圆被分在两块硬纸片中的面积也相等.你认为小丽的想法能实现吗 若能,请你画图说明剪的方法.
22.(10分)如图,P是∠AOB的平分线OC上的一点,过点P分别作OA,OB的垂线,垂足分别为点D,H,E是线段OD上一点,F是线段OH上一点,EF与OC交于点G,且DE=FH.
求证:OP是线段EF的垂直平分线.
23.(10分)如图所示,在△ABC中:
(1)下列操作中,作∠ABC的平分线的正确顺序是 (将序号按正确的顺序写在横线上).
①分别以点M,N为圆心,适当长为半径作圆弧,在∠ABC内,两弧交于点P;
②以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于点N;
③画射线BP,交AC于点D.
(2)能说明∠ABD=∠CBD的作图依据是 (填序号).
①SSS;②ASA;③AAS;④角平分线上的点到这个角的两边的距离相等.
(3)若AB=18,BC=12,=120,过点D作DE⊥AB于点E,求DE的长.
24.(12分)(2025松江宁江区期中)如图,在△ABC中,边AB的垂直平分线EF分别交边BC,AB于点E,F,过点A作AD⊥BC于点D,且D为线段CE的中点.
(1)求证:BE=AC.
(2)若∠B=35°,求∠EAD的度数.
【详解答案】
1.C 解析:A.是轴对称图形,不是中心对称图形;B.是中心对称图形,不是轴对称图形;C.既是轴对称图形,又是中心对称图形;D.是轴对称图形,不是中心对称图形.故选C.
2.B 解析:A中,顺时针连续旋转60°即可得到;C中,旋转180°即可得到;D中,旋转60°即可得到.故选B.
3.B 解析:根据中心对称图形的定义可知,只有在②位置再涂上一个正方形,才是中心对称图形.故选B.
4.D 解析:A.两个三角形全等,它们不一定关于某条直线对称,故A错误;B.两个图形关于某条直线对称,对应点不一定在直线两旁,还有可能在直线上,故B错误;C.成轴对称的两个图形的对应点连线的垂直平分线,就是它们的对称轴,故C错误;D.关于某条直线对称的两个三角形是全等三角形,故D正确.故选D.
5.A 解析:在镜子上看到的数字是15:01,那么真实数字应该是将此数字反转,为10:21.故选A.
6.C 解析:∵DE是AB的垂直平分线,AE=4,∴EB=EA=4.∴BC=EB+EC=4+2=6.故选C.
7.B 解析:根据轴对称的性质,得∠x=180°-70°-75°=35°.故选B.
8.C 解析:根据原图中小圆的位置可排除A,B;根据原图中小三角形的形状可排除D.故选C.
9.D 解析:如图,过点D作DF⊥AC于点F.∵AD是∠BAC的平分线,DE⊥AB,∴DE=DF.∵DE=2,∴DF=2,由图可知,S△ABC=S△ABD+S△ACD,∵AC=4,∴×AB×2+×4×2=9,解得AB=5.故选D.
10.B 解析:根据点B与点C关于点A成中心对称,得到线段AC=4,将点A向左平移4个单位长度得到点C,所以点C表示的数为-1-4=-5.故选B.
11.D 解析:∵AD平分∠BAC,∴∠BAD=∠CAD.又∵AB=AC,AD=AD,∴△ABD≌△ACD(SAS).∴BD=CD,∠BDA=∠CDA=90°,即AD⊥BC,∴③正确.∴AD是BC的垂直平分线,∴①正确.∵AD平分∠BAC,∴②正确.∵△ABD≌△ACD,∴∠B=∠C.又∵∠BED=∠CFD,BD=CD,∴△BED≌△CFD(AAS),∴∠BDE=∠CDF,∴④正确.故选D.
12.B
解析:如图,连接PC.∵AB=AC,BD=CD,∴点A,D在BC的垂直平分线上.∴AD为线段BC的垂直平分线.∴PB=PC.∴PB+PE=PC+PE.∵PE+PC≥CE,∴P,C,E三点在同一条直线上时,PB+PE的值最小,最小值为CE的长度.故选B.
13.1
14.95° 解析:∵△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,∴∠C=∠ABO=∠DBO=15°,∠D=∠BAO=∠OAC=25°,∴∠CAB=50°,∴∠BOC=∠BAC+∠C+∠ABO=80°,∴∠BEC=∠BOC+∠OBD=80°+15°=95°.
15.2 解析:连接AC,如图所示,∵弧OA与弧OC关于点O中心对称,∴点O为边AC的中点.∴弓形OA的面积=弓形OC的面积.∴AB,BC,弧OC,弧OA所围成的图形面积=△BAC的面积=×2×2=2(cm2).
16.3 解析:如图,过点P作PM⊥AB于点M,
∵BD垂直平分线段AC,∴AB=CB,
AD=CD,又∵BD=BD,
∴△ABD≌△CBD(SSS),
∴∠ABD=∠DBC,
即BD为∠ABC的平分线,
又∵PM⊥AB,PE⊥CB,
∴PM=PE=3 cm.
17.解:如图,点P即为所求.
18.解:(1)如图1所示.(答案不唯一)
(2)如图2所示.
(3)如图3所示.(答案不唯一)
图1 图2 图3
19.证明:∵OE⊥AD,AE=DE,∴直线OE是线段AD的垂直平分线.由对称性知∠OAE=∠ODE.∴∠BAO=∠BAD-∠OAE=∠CDA-∠ODE=∠CDO.
∵直线OE是线段AD的垂直平分线,∴OA=OD.
在△AOB和△DOC中,
∴△AOB≌△DOC(ASA).
∴OB=OC.∴O在线段BC的垂直平分线上,即线段BC的垂直平分线一定经过点O.
20.证明:∵AD平分∠CAB,DE⊥AB,∠C=90°,∴DC=DE,∠C=∠BED=90°.
在△DCF和△DEB中,
∵
∴△DCF≌△DEB(SAS).
∴BD=DF.
21.解:能.方法为:
(1)连接长方形的两条对角线,设两条对角线交于O点.
(2)设圆的圆心为O',过点O和O'画直线m.
(3)沿直线m将长方形硬纸片剪开,则得到符合要求的两张硬纸片,如图所示.
22.证明:∵OP平分∠AOB,
∴∠HOP=∠DOP,
∵PD⊥OA,PH⊥OB,
∴∠OHP=∠ODP=90°,
在△HOP和△DOP中,
∴△HOP≌△DOP(AAS).
∴OH=OD,
∵DE=FH,∴OE=OF.
在△EOG和△FOG中,
∴△EOG≌△FOG(SAS).
∴∠EGO=∠FGO=90°,EG=FG,
∴OP垂直平分线段EF,即OP是线段EF的垂直平分线.
23.解:(1)②①③ (2)①
(3)如图,过点D作DF⊥BC于点F.
∵∠ABD=∠CBD,
DE⊥AB,DF⊥BC,
∴DE=DF.
∵S△ABC=S△ABD+S△CBD,
即×AB×DE+×BC×DF=120,
∴×18×DE+×12×DE=120.解得DE=8.
24.解:(1)证明:连接AE,如图所示.
∵AD⊥BC于点D,且D为线段CE的中点,
∴AD垂直平分CE,
∴AC=AE,
∵EF垂直平分AB,
∴AE=BE,
∴BE=AC.
(2)∵EF垂直平分AB,∠B=35°,
∴由对称性可得∠BAE=∠B=35°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=180°-90°-35°=55°,
∴∠EAD=55°-35°=20°.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024淄博中考)下列图案中,既是轴对称图形又是中心对称图形的是 ( )
A B C D
2.如图所示的图案是由六个全等的菱形(各边相等的四边形)拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的是 ( )
A B C D
3.如图是一个由六个正方形组成的网格.现在嘉嘉想再涂上一个正方形,使四个阴影正方形所组成的图形是中心对称图形,则嘉嘉应该涂 ( )
A.①或② B.②
C.②或③ D.③
4.下列说法中,正确的是 ( )
A.两个全等的三角形一定关于某条直线对称
B.两个图形关于某条直线对称,对应点一定在直线两旁
C.成轴对称的两个图形的对应点连线的垂线,就是它们的对称轴
D.关于某条直线对称的两个三角形是全等三角形
5.如图,是小亮在某时刻从镜子里看到镜子对面电子钟的像,则这个时刻是 ( )
A.10:21 B.10:51
C.21:10 D.15:01
6.如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,连接AE.若AE=4,EC=2,则BC的长是 ( )
A.2 B.4 C.6 D.8
7.如图所示,图中的两个三角形关于直线l成轴对称,根据图中标注的数据,得∠x的度数为 ( )
A.25° B.35° C.40° D.70°
8.如图所示的长方形纸片,先沿虚线按箭头方向向右对折,接着将对折后的纸片沿虚线剪下一个小圆和一个小三角形,然后将纸片打开是下列图中的哪一个 ( )
A B C D
9.(2025承德期末)如图,AD是∠BAC的平分线,DE⊥AB于点E,S△ABC=9,DE=2,AC=4,则AB的长是( )
A.3 B.4 C.6 D.5
10.数轴上点A,B的位置如图所示,若点B关于点A的对称点为C,则点C表示的数为 ( )
A.3 B.-5 C.5 D.-3
11.如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,则下列四个结论:①AD上任意一点到点C、点B的距离相等;②AD上任意一点到AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.其中,正确的个数是 ( )
A.1 B.2 C.3 D.4
12.如图,在△ABC中,AB=AC,AD,CE是△ABC的两条中线,P是AD上一个动点,则下列线段的长度等于PB+PE的最小值的是 ( )
A.BC B.CE C.AD D.AC
二、填空题(本大题共4个小题,每小题3分,共12分)
13.如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= .
14.如图,△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,OC与BD交于点E.若∠C=15°,∠D=25°,则∠BEC的度数为 .
15.如图,AB⊥BC,AB=BC=2 cm,弧OA与弧OC关于点O中心对称,则线段AB,BC,弧OC,弧OA所围成的图形面积是 cm2.
16.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于点P,PE=3 cm,则P点到直线AB的距离是 cm.
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)如图,已知锐角三角形ABC,∠B=48°,请用尺规作图法,在△ABC内部求作一点P.使PB=PC,且∠PBC=24°.(保留作图痕迹,不写作法)
18.(8分)如图所示,在7×6的正方形网格中,选取14个格点,以其中三个格点为顶点画出△ABC,请你以选取的格点为顶点再画出一个三角形,且分别满足下列条件:
(1)图1中所画的三角形与△ABC组成的图形是轴对称图形.
(2)图2中所画的三角形与△ABC组成的图形是中心对称图形.
(3)图3中所画的三角形与△ABC的面积相等,但不全等.
图1 图2 图3
19.(8分)如图所示,O是四边形ABCD中的一点,AB=CD,∠AOB=∠COD,∠BAD=∠CDA,作OE⊥AD,垂足为E,若AE=DE.
求证:线段BC的垂直平分线一定经过点O.
20.(8分)如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.
求证:BD=DF.
21.(8分)如图所示,在长方形硬纸片的右下角画有一个圆,小丽想把这张硬纸片剪成两块,使两块硬纸片的面积相等,并且圆被分在两块硬纸片中的面积也相等.你认为小丽的想法能实现吗 若能,请你画图说明剪的方法.
22.(10分)如图,P是∠AOB的平分线OC上的一点,过点P分别作OA,OB的垂线,垂足分别为点D,H,E是线段OD上一点,F是线段OH上一点,EF与OC交于点G,且DE=FH.
求证:OP是线段EF的垂直平分线.
23.(10分)如图所示,在△ABC中:
(1)下列操作中,作∠ABC的平分线的正确顺序是 (将序号按正确的顺序写在横线上).
①分别以点M,N为圆心,适当长为半径作圆弧,在∠ABC内,两弧交于点P;
②以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于点N;
③画射线BP,交AC于点D.
(2)能说明∠ABD=∠CBD的作图依据是 (填序号).
①SSS;②ASA;③AAS;④角平分线上的点到这个角的两边的距离相等.
(3)若AB=18,BC=12,=120,过点D作DE⊥AB于点E,求DE的长.
24.(12分)(2025松江宁江区期中)如图,在△ABC中,边AB的垂直平分线EF分别交边BC,AB于点E,F,过点A作AD⊥BC于点D,且D为线段CE的中点.
(1)求证:BE=AC.
(2)若∠B=35°,求∠EAD的度数.
【详解答案】
1.C 解析:A.是轴对称图形,不是中心对称图形;B.是中心对称图形,不是轴对称图形;C.既是轴对称图形,又是中心对称图形;D.是轴对称图形,不是中心对称图形.故选C.
2.B 解析:A中,顺时针连续旋转60°即可得到;C中,旋转180°即可得到;D中,旋转60°即可得到.故选B.
3.B 解析:根据中心对称图形的定义可知,只有在②位置再涂上一个正方形,才是中心对称图形.故选B.
4.D 解析:A.两个三角形全等,它们不一定关于某条直线对称,故A错误;B.两个图形关于某条直线对称,对应点不一定在直线两旁,还有可能在直线上,故B错误;C.成轴对称的两个图形的对应点连线的垂直平分线,就是它们的对称轴,故C错误;D.关于某条直线对称的两个三角形是全等三角形,故D正确.故选D.
5.A 解析:在镜子上看到的数字是15:01,那么真实数字应该是将此数字反转,为10:21.故选A.
6.C 解析:∵DE是AB的垂直平分线,AE=4,∴EB=EA=4.∴BC=EB+EC=4+2=6.故选C.
7.B 解析:根据轴对称的性质,得∠x=180°-70°-75°=35°.故选B.
8.C 解析:根据原图中小圆的位置可排除A,B;根据原图中小三角形的形状可排除D.故选C.
9.D 解析:如图,过点D作DF⊥AC于点F.∵AD是∠BAC的平分线,DE⊥AB,∴DE=DF.∵DE=2,∴DF=2,由图可知,S△ABC=S△ABD+S△ACD,∵AC=4,∴×AB×2+×4×2=9,解得AB=5.故选D.
10.B 解析:根据点B与点C关于点A成中心对称,得到线段AC=4,将点A向左平移4个单位长度得到点C,所以点C表示的数为-1-4=-5.故选B.
11.D 解析:∵AD平分∠BAC,∴∠BAD=∠CAD.又∵AB=AC,AD=AD,∴△ABD≌△ACD(SAS).∴BD=CD,∠BDA=∠CDA=90°,即AD⊥BC,∴③正确.∴AD是BC的垂直平分线,∴①正确.∵AD平分∠BAC,∴②正确.∵△ABD≌△ACD,∴∠B=∠C.又∵∠BED=∠CFD,BD=CD,∴△BED≌△CFD(AAS),∴∠BDE=∠CDF,∴④正确.故选D.
12.B
解析:如图,连接PC.∵AB=AC,BD=CD,∴点A,D在BC的垂直平分线上.∴AD为线段BC的垂直平分线.∴PB=PC.∴PB+PE=PC+PE.∵PE+PC≥CE,∴P,C,E三点在同一条直线上时,PB+PE的值最小,最小值为CE的长度.故选B.
13.1
14.95° 解析:∵△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,∴∠C=∠ABO=∠DBO=15°,∠D=∠BAO=∠OAC=25°,∴∠CAB=50°,∴∠BOC=∠BAC+∠C+∠ABO=80°,∴∠BEC=∠BOC+∠OBD=80°+15°=95°.
15.2 解析:连接AC,如图所示,∵弧OA与弧OC关于点O中心对称,∴点O为边AC的中点.∴弓形OA的面积=弓形OC的面积.∴AB,BC,弧OC,弧OA所围成的图形面积=△BAC的面积=×2×2=2(cm2).
16.3 解析:如图,过点P作PM⊥AB于点M,
∵BD垂直平分线段AC,∴AB=CB,
AD=CD,又∵BD=BD,
∴△ABD≌△CBD(SSS),
∴∠ABD=∠DBC,
即BD为∠ABC的平分线,
又∵PM⊥AB,PE⊥CB,
∴PM=PE=3 cm.
17.解:如图,点P即为所求.
18.解:(1)如图1所示.(答案不唯一)
(2)如图2所示.
(3)如图3所示.(答案不唯一)
图1 图2 图3
19.证明:∵OE⊥AD,AE=DE,∴直线OE是线段AD的垂直平分线.由对称性知∠OAE=∠ODE.∴∠BAO=∠BAD-∠OAE=∠CDA-∠ODE=∠CDO.
∵直线OE是线段AD的垂直平分线,∴OA=OD.
在△AOB和△DOC中,
∴△AOB≌△DOC(ASA).
∴OB=OC.∴O在线段BC的垂直平分线上,即线段BC的垂直平分线一定经过点O.
20.证明:∵AD平分∠CAB,DE⊥AB,∠C=90°,∴DC=DE,∠C=∠BED=90°.
在△DCF和△DEB中,
∵
∴△DCF≌△DEB(SAS).
∴BD=DF.
21.解:能.方法为:
(1)连接长方形的两条对角线,设两条对角线交于O点.
(2)设圆的圆心为O',过点O和O'画直线m.
(3)沿直线m将长方形硬纸片剪开,则得到符合要求的两张硬纸片,如图所示.
22.证明:∵OP平分∠AOB,
∴∠HOP=∠DOP,
∵PD⊥OA,PH⊥OB,
∴∠OHP=∠ODP=90°,
在△HOP和△DOP中,
∴△HOP≌△DOP(AAS).
∴OH=OD,
∵DE=FH,∴OE=OF.
在△EOG和△FOG中,
∴△EOG≌△FOG(SAS).
∴∠EGO=∠FGO=90°,EG=FG,
∴OP垂直平分线段EF,即OP是线段EF的垂直平分线.
23.解:(1)②①③ (2)①
(3)如图,过点D作DF⊥BC于点F.
∵∠ABD=∠CBD,
DE⊥AB,DF⊥BC,
∴DE=DF.
∵S△ABC=S△ABD+S△CBD,
即×AB×DE+×BC×DF=120,
∴×18×DE+×12×DE=120.解得DE=8.
24.解:(1)证明:连接AE,如图所示.
∵AD⊥BC于点D,且D为线段CE的中点,
∴AD垂直平分CE,
∴AC=AE,
∵EF垂直平分AB,
∴AE=BE,
∴BE=AC.
(2)∵EF垂直平分AB,∠B=35°,
∴由对称性可得∠BAE=∠B=35°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=180°-90°-35°=55°,
∴∠EAD=55°-35°=20°.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
