第十六章 专题训练八 线段垂直平分线、角的平分线相关问题及应用 同步练 (含答案)2025-2026学年数学冀教版(2024)八年级上册
文档属性
| 名称 | 第十六章 专题训练八 线段垂直平分线、角的平分线相关问题及应用 同步练 (含答案)2025-2026学年数学冀教版(2024)八年级上册 | 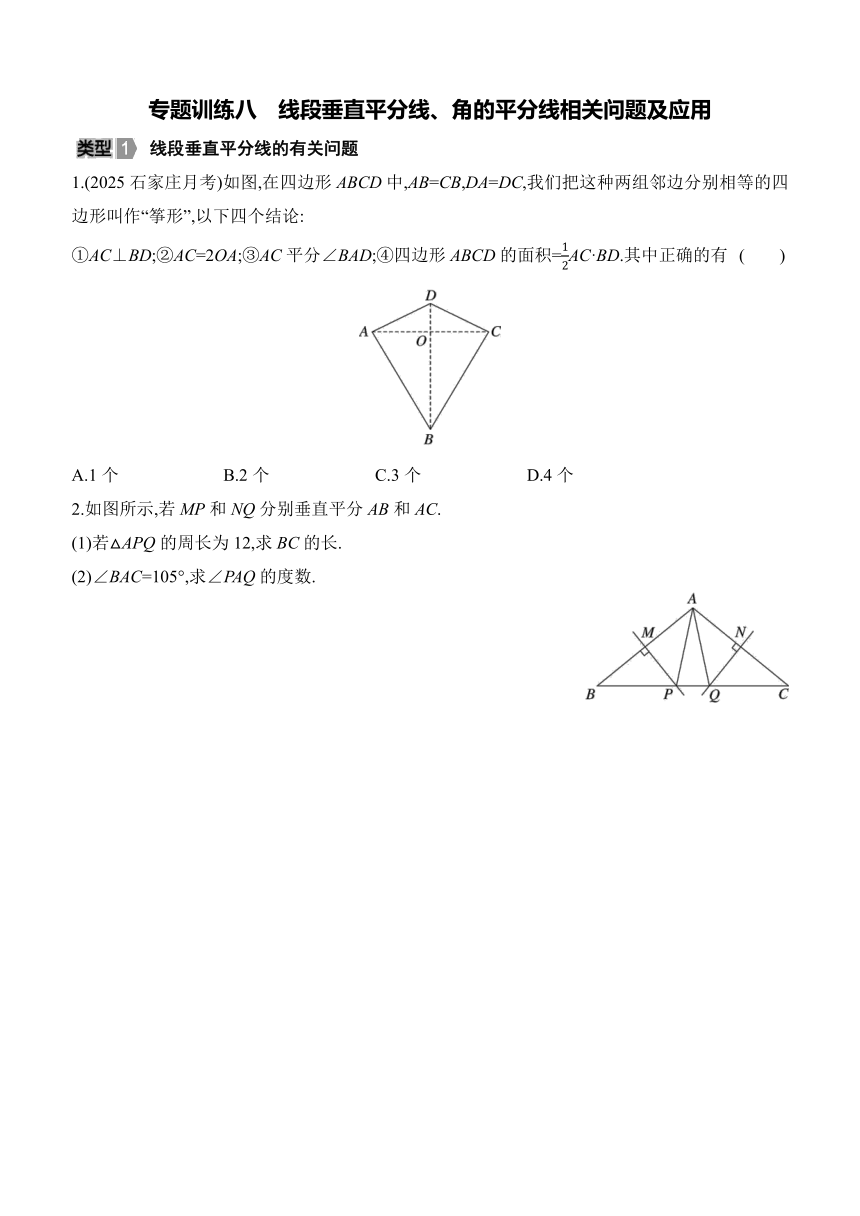 | |
| 格式 | docx | ||
| 文件大小 | 203.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 13:30:43 | ||
图片预览



文档简介
专题训练八 线段垂直平分线、角的平分线相关问题及应用
线段垂直平分线的有关问题
1.(2025石家庄月考)如图,在四边形ABCD中,AB=CB,DA=DC,我们把这种两组邻边分别相等的四边形叫作“筝形”,以下四个结论:
①AC⊥BD;②AC=2OA;③AC平分∠BAD;④四边形ABCD的面积=AC·BD.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
2.如图所示,若MP和NQ分别垂直平分AB和AC.
(1)若△APQ的周长为12,求BC的长.
(2)∠BAC=105°,求∠PAQ的度数.
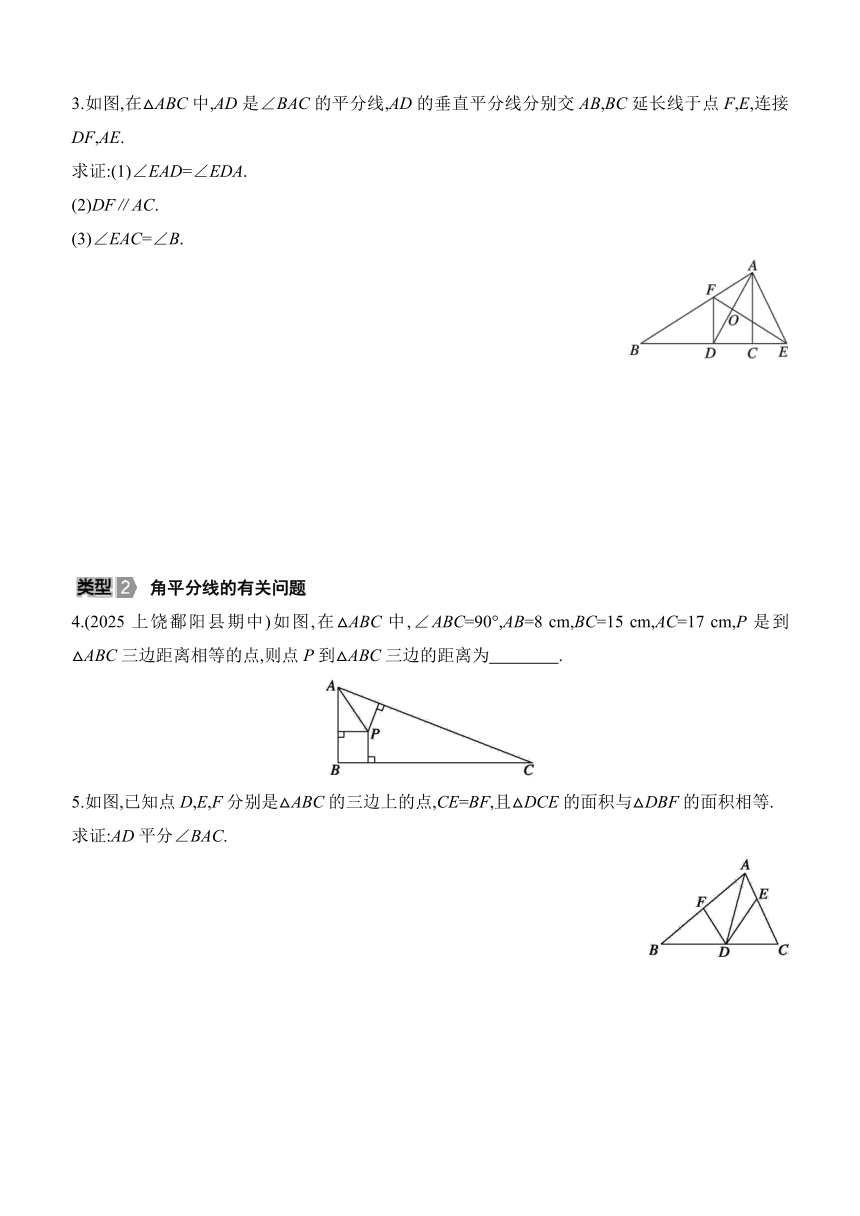
3.如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线分别交AB,BC延长线于点F,E,连接DF,AE.
求证:(1)∠EAD=∠EDA.
(2)DF∥AC.
(3)∠EAC=∠B.
角平分线的有关问题
4.(2025上饶鄱阳县期中)如图,在△ABC中,∠ABC=90°,AB=8 cm,BC=15 cm,AC=17 cm,P是到△ABC三边距离相等的点,则点P到△ABC三边的距离为 .
5.如图,已知点D,E,F分别是△ABC的三边上的点,CE=BF,且△DCE的面积与△DBF的面积相等.
求证:AD平分∠BAC.
6.(2025唐山月考)如图,在△ABC中,点D在边BC上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数.
(2)若AB=7,AD=4,CD=8且S△ACD=15,求△ABE的面积.
有关“相等”的尺规作图问题
7.(新情境)如图,某学校甬路中央有一幅大型壁画AB,现要在壁画正前方立一旗杆,且旗杆到壁画AB的距离是壁画长度的一半,请你利用尺规作图的方法确定旗杆的位置,写出画法,保留作图痕迹.
最短路径问题
8.如图,在△ABC中,AB=4,AC=6,FE垂直平分线段BC,P是直线EF上的任意一点,求△ABP周长的最小值.
9.如图所示,点M是锐角∠AOB内部的一点.请你在边OA和边OB上分别找到点P,Q,使得△MPQ的周长最小.
【详解答案】
1.C 解析:∵AB=CB,DA=DC,∴DB垂直平分线段AC,∴AC⊥BD,故①正确;AC=2OA,故②正确;四边形ABCD的面积=S△ADB+S△BCD=DB·OA+DB·OC=DB·AC,故④正确;无法得出AC平分∠BAD,故③错误.故选C.
2.解:(1)∵MP和NQ分别垂直平分AB和AC,∴AP=BP,AQ=CQ.
∴△APQ的周长=AP+PQ+AQ=BP+PQ+CQ=BC.
∵△APQ的周长为12,
∴BC=12.
(2)∵AP=BP,AM=BM,MP=MP,
∴△APM≌△BPM(SSS).
∴∠B=∠BAP.
同理,∠C=∠CAQ.∵∠BAC=105°,
∴∠BAP+∠CAQ=∠B+∠C=180°-∠BAC=180°-105°=75°.
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=105°-75°=30°.
3.证明:(1)∵EF是AD的垂直平分线,
∴AE=DE,AO=DO,又OE=OE,
∴△AOE≌△DOE(SSS).
∴∠EAD=∠EDA.
(2)∵EF是AD的垂直平分线,
∴AF=DF,AO=DO,又OF=OF,
∴△AOF≌△DOF(SSS).
∴∠FAD=∠FDA.
∵AD是∠BAC的平分线,
∴∠FAD=∠CAD.
∴∠FDA=∠CAD.
∴DF∥AC.
(3)∵∠EAC=∠EAD-∠CAD,
∠B=∠EDA-∠BAD,
且∠BAD=∠CAD,∠EAD=∠EDA,
∴∠EAC=∠B.
4.3 cm 解析:设P到△ABC三边距离为x cm,PD⊥AB于D点,PE⊥BC于E点,PF⊥AC于F点,如图,则PD=PE=PF=x cm,连接PC,PB,∵S△APB+S△PBC+S△APC=S△ABC,∴×8·x+×15·x+×17·x=×8×15,解得x=3,即点P到△ABC三边的距离为3 cm.
5.证明:过D作DM⊥AB于点M,DN⊥AC于点N,如图所示.
∵△DCE的面积与△DBF的面积相等,
∴CE·DN=BF·DM,
∵CE=BF,
∴DN=DM.
∴点D在∠BAC的平分线上.
∴AD平分∠BAC.
6.解:(1)∵EF⊥AB, ∠AEF=50°,
∴∠FAE=180°-90°-50°=40°.
∵∠BAD=100°,
∴∠CAD=180°-100°-40°=40°.
(2)如图,过点E作EG⊥AD于点G,EH⊥BC于点H.
设EG=x,由(1)得∠FAE=∠CAD,
∴CA为∠DAF的平分线.
又EF⊥AB,EG⊥AD,
∴EF=EG.
∵BE是∠ABC的平分线,
∴EF=EH.
∴EG=EH.
∴EF=EH=EG=x.
∵S△ACD=15,AD=4,CD=8,
∴AD·EG+CD·EH=15,
即4x+8x=30.
解得x=.
∴EF=.
∴S△ABE=AB·EF=×7×.
7.解:作法如下:
(1)作AB的垂直平分线EF,设直线EF交AB于点M.
(2)以M为圆心、MA为半径画弧,与直线EF交于点P,则P点即为旗杆的位置.如图所示.
8.解:如图,连接PC,
∵EF垂直平分线段BC,
∴PB=PC,
∴PA+PB=PA+PC≥AC=6,
∴PA+PB的最小值为6,
∴△ABP的周长的最小值为6+4=10.
9.解:如图所示,作出点M关于OA的对称点M',点M关于OB的对称点M″,连接M'M″,交OA于点P,交OB于点Q,此时△MPQ的周长最小.
线段垂直平分线的有关问题
1.(2025石家庄月考)如图,在四边形ABCD中,AB=CB,DA=DC,我们把这种两组邻边分别相等的四边形叫作“筝形”,以下四个结论:
①AC⊥BD;②AC=2OA;③AC平分∠BAD;④四边形ABCD的面积=AC·BD.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
2.如图所示,若MP和NQ分别垂直平分AB和AC.
(1)若△APQ的周长为12,求BC的长.
(2)∠BAC=105°,求∠PAQ的度数.
3.如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线分别交AB,BC延长线于点F,E,连接DF,AE.
求证:(1)∠EAD=∠EDA.
(2)DF∥AC.
(3)∠EAC=∠B.
角平分线的有关问题
4.(2025上饶鄱阳县期中)如图,在△ABC中,∠ABC=90°,AB=8 cm,BC=15 cm,AC=17 cm,P是到△ABC三边距离相等的点,则点P到△ABC三边的距离为 .
5.如图,已知点D,E,F分别是△ABC的三边上的点,CE=BF,且△DCE的面积与△DBF的面积相等.
求证:AD平分∠BAC.
6.(2025唐山月考)如图,在△ABC中,点D在边BC上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数.
(2)若AB=7,AD=4,CD=8且S△ACD=15,求△ABE的面积.
有关“相等”的尺规作图问题
7.(新情境)如图,某学校甬路中央有一幅大型壁画AB,现要在壁画正前方立一旗杆,且旗杆到壁画AB的距离是壁画长度的一半,请你利用尺规作图的方法确定旗杆的位置,写出画法,保留作图痕迹.
最短路径问题
8.如图,在△ABC中,AB=4,AC=6,FE垂直平分线段BC,P是直线EF上的任意一点,求△ABP周长的最小值.
9.如图所示,点M是锐角∠AOB内部的一点.请你在边OA和边OB上分别找到点P,Q,使得△MPQ的周长最小.
【详解答案】
1.C 解析:∵AB=CB,DA=DC,∴DB垂直平分线段AC,∴AC⊥BD,故①正确;AC=2OA,故②正确;四边形ABCD的面积=S△ADB+S△BCD=DB·OA+DB·OC=DB·AC,故④正确;无法得出AC平分∠BAD,故③错误.故选C.
2.解:(1)∵MP和NQ分别垂直平分AB和AC,∴AP=BP,AQ=CQ.
∴△APQ的周长=AP+PQ+AQ=BP+PQ+CQ=BC.
∵△APQ的周长为12,
∴BC=12.
(2)∵AP=BP,AM=BM,MP=MP,
∴△APM≌△BPM(SSS).
∴∠B=∠BAP.
同理,∠C=∠CAQ.∵∠BAC=105°,
∴∠BAP+∠CAQ=∠B+∠C=180°-∠BAC=180°-105°=75°.
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=105°-75°=30°.
3.证明:(1)∵EF是AD的垂直平分线,
∴AE=DE,AO=DO,又OE=OE,
∴△AOE≌△DOE(SSS).
∴∠EAD=∠EDA.
(2)∵EF是AD的垂直平分线,
∴AF=DF,AO=DO,又OF=OF,
∴△AOF≌△DOF(SSS).
∴∠FAD=∠FDA.
∵AD是∠BAC的平分线,
∴∠FAD=∠CAD.
∴∠FDA=∠CAD.
∴DF∥AC.
(3)∵∠EAC=∠EAD-∠CAD,
∠B=∠EDA-∠BAD,
且∠BAD=∠CAD,∠EAD=∠EDA,
∴∠EAC=∠B.
4.3 cm 解析:设P到△ABC三边距离为x cm,PD⊥AB于D点,PE⊥BC于E点,PF⊥AC于F点,如图,则PD=PE=PF=x cm,连接PC,PB,∵S△APB+S△PBC+S△APC=S△ABC,∴×8·x+×15·x+×17·x=×8×15,解得x=3,即点P到△ABC三边的距离为3 cm.
5.证明:过D作DM⊥AB于点M,DN⊥AC于点N,如图所示.
∵△DCE的面积与△DBF的面积相等,
∴CE·DN=BF·DM,
∵CE=BF,
∴DN=DM.
∴点D在∠BAC的平分线上.
∴AD平分∠BAC.
6.解:(1)∵EF⊥AB, ∠AEF=50°,
∴∠FAE=180°-90°-50°=40°.
∵∠BAD=100°,
∴∠CAD=180°-100°-40°=40°.
(2)如图,过点E作EG⊥AD于点G,EH⊥BC于点H.
设EG=x,由(1)得∠FAE=∠CAD,
∴CA为∠DAF的平分线.
又EF⊥AB,EG⊥AD,
∴EF=EG.
∵BE是∠ABC的平分线,
∴EF=EH.
∴EG=EH.
∴EF=EH=EG=x.
∵S△ACD=15,AD=4,CD=8,
∴AD·EG+CD·EH=15,
即4x+8x=30.
解得x=.
∴EF=.
∴S△ABE=AB·EF=×7×.
7.解:作法如下:
(1)作AB的垂直平分线EF,设直线EF交AB于点M.
(2)以M为圆心、MA为半径画弧,与直线EF交于点P,则P点即为旗杆的位置.如图所示.
8.解:如图,连接PC,
∵EF垂直平分线段BC,
∴PB=PC,
∴PA+PB=PA+PC≥AC=6,
∴PA+PB的最小值为6,
∴△ABP的周长的最小值为6+4=10.
9.解:如图所示,作出点M关于OA的对称点M',点M关于OB的对称点M″,连接M'M″,交OA于点P,交OB于点Q,此时△MPQ的周长最小.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
