第十六章 轴对称和中心对称 专题训练九 尺规作图 同步练(含答案) 2025-2026学年数学冀教版(2024)八年级上册
文档属性
| 名称 | 第十六章 轴对称和中心对称 专题训练九 尺规作图 同步练(含答案) 2025-2026学年数学冀教版(2024)八年级上册 | 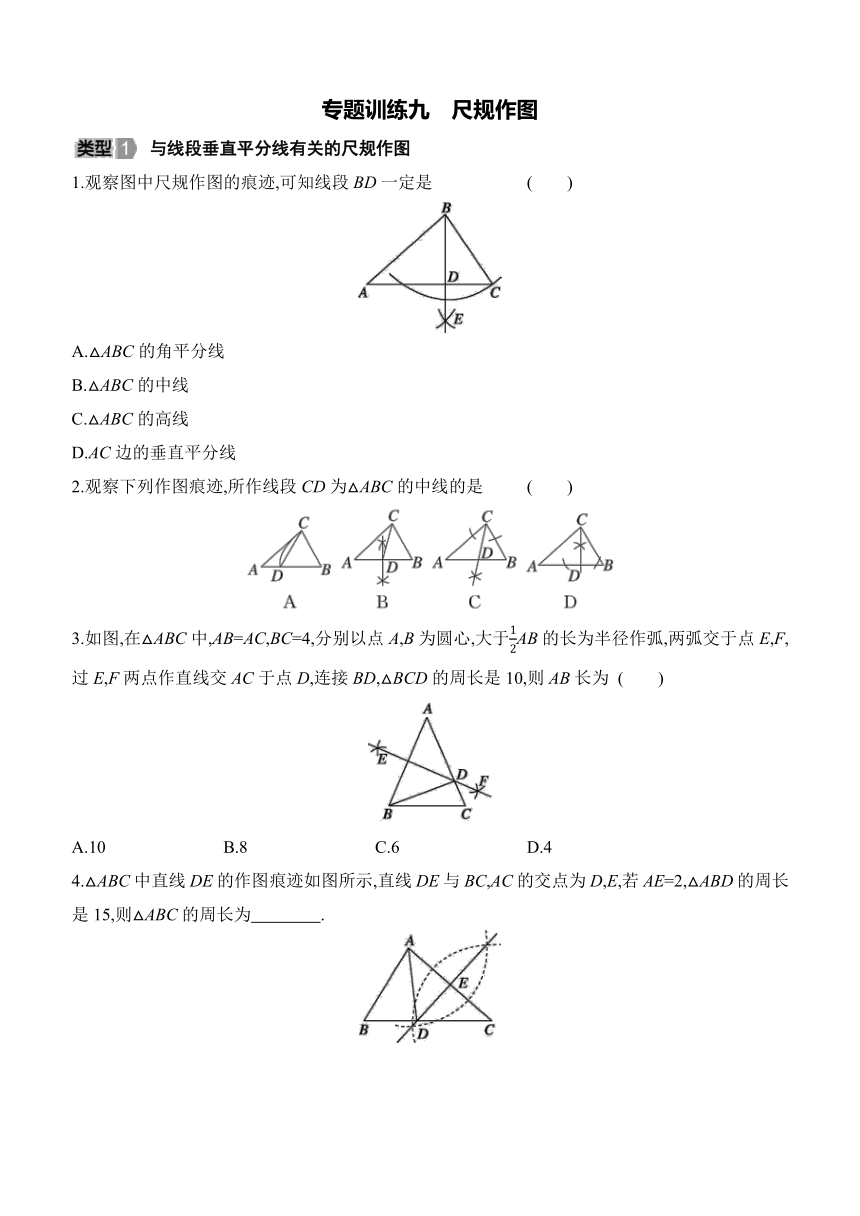 | |
| 格式 | docx | ||
| 文件大小 | 196.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 13:30:59 | ||
图片预览


文档简介
专题训练九 尺规作图
与线段垂直平分线有关的尺规作图
1.观察图中尺规作图的痕迹,可知线段BD一定是 ( )
A.△ABC的角平分线
B.△ABC的中线
C.△ABC的高线
D.AC边的垂直平分线
2.观察下列作图痕迹,所作线段CD为△ABC的中线的是 ( )
3.如图,在△ABC中,AB=AC,BC=4,分别以点A,B为圆心,大于AB的长为半径作弧,两弧交于点E,F,过E,F两点作直线交AC于点D,连接BD,△BCD的周长是10,则AB长为 ( )
A.10 B.8 C.6 D.4
4.△ABC中直线DE的作图痕迹如图所示,直线DE与BC,AC的交点为D,E,若AE=2,△ABD的周长是15,则△ABC的周长为 .
5.(教材变式)如图所示,某地有三个相邻的食品加工厂A,B,C,现计划建一个食品中转站,使中转站到三个食品加工厂的距离相等,请你利用尺规作图的方法,确定中转站的位置并说明理由.
6.(2025邢台威县月考)如图,汽车站、码头分别位于A,B两点,直线m,n分别表示公路与河流.
(1)从汽车站A到码头B怎样走最近 利用尺规作图的方法画出最近路线,并说明理由.
(2)从码头B到公路m怎样走最近 画出最近路线BC,并说明理由.
(3)在(1)(2)的基础上,比较AC和AB的大小,并说明理由.
与角平分线有关的尺规作图
7.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,适当长为半径画弧,两弧交于点P,作射线AP交BC于点D,若△ABC的面积是16,AB+AC=16,则CD的长为 ( )
A.1 B.2 C.3 D.4
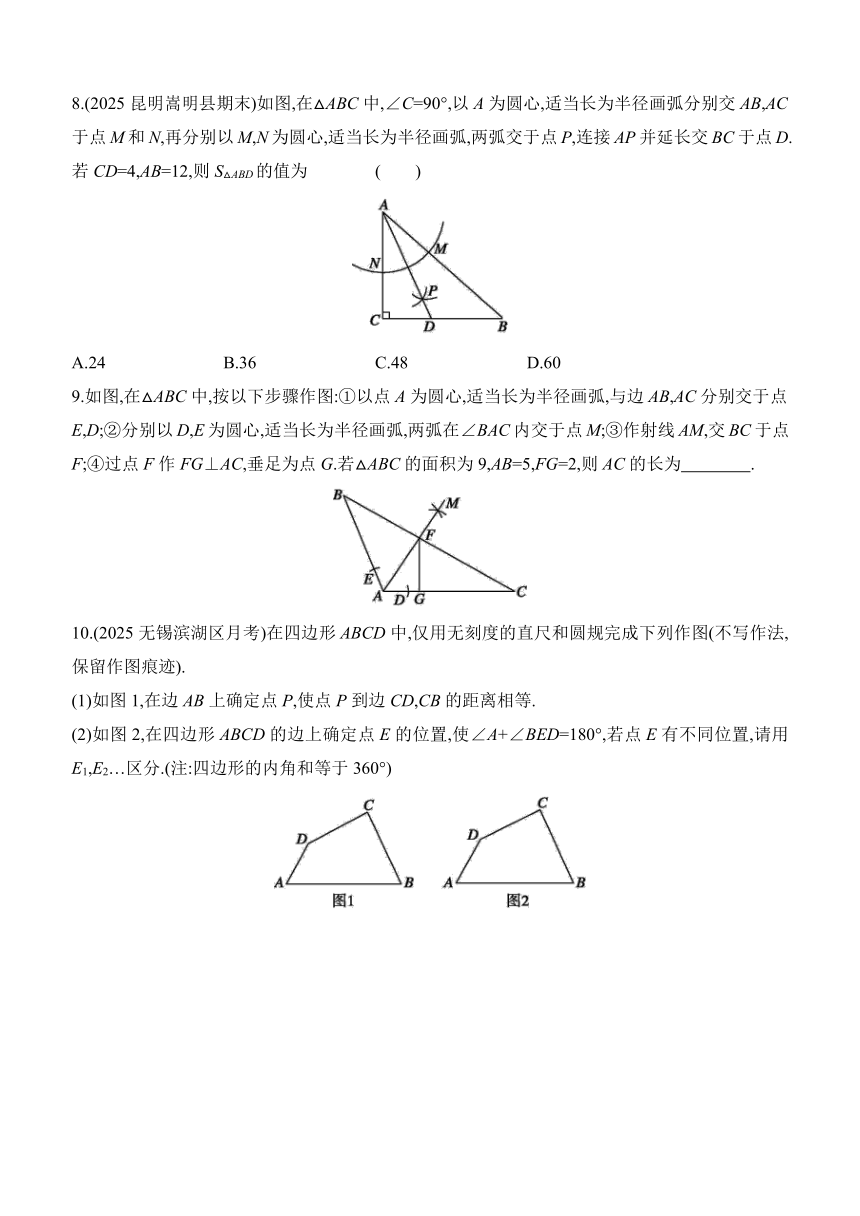
8.(2025昆明嵩明县期末)如图,在△ABC中,∠C=90°,以A为圆心,适当长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,适当长为半径画弧,两弧交于点P,连接AP并延长交BC于点D.若CD=4,AB=12,则S△ABD的值为 ( )
A.24 B.36 C.48 D.60
9.如图,在△ABC中,按以下步骤作图:①以点A为圆心,适当长为半径画弧,与边AB,AC分别交于点E,D;②分别以D,E为圆心,适当长为半径画弧,两弧在∠BAC内交于点M;③作射线AM,交BC于点F;④过点F作FG⊥AC,垂足为点G.若△ABC的面积为9,AB=5,FG=2,则AC的长为 .
10.(2025无锡滨湖区月考)在四边形ABCD中,仅用无刻度的直尺和圆规完成下列作图(不写作法,保留作图痕迹).
(1)如图1,在边AB上确定点P,使点P到边CD,CB的距离相等.
(2)如图2,在四边形ABCD的边上确定点E的位置,使∠A+∠BED=180°,若点E有不同位置,请用E1,E2…区分.(注:四边形的内角和等于360°)
与线段垂直平分线、角平分线都有关的尺规作图
11.(2025呼和浩特回民区期中)如图,在△ABC中,利用直尺和圆规完成下列作图.
(1)作∠ABC的平分线,线段AB的垂直平分线,保留作图痕迹.
(2)在(1)中,所作角平分线与垂直平分线相交于点F,连接AF,若∠ACB=60°,∠CAF=24°,则∠BAF的度数是多少
【详解答案】
1.C
2.B 解析:A.可得BC=BD,不符合题意;B.CD为△ABC的边AB上的中线,符合题意;C.CD是∠ACB的平分线,不符合题意;D.CD⊥AB,但不平分,不符合题意.故选B.
3.C 解析:由作图过程可知EF是线段AB的垂直平分线,∴AD=BD,∴△BCD的周长=BC+CD+BD=BC+CD+AD=BC+AC=4+AC=10,∴AC=6,∴AB=AC=6.故选C.
4.19 解析:根据作图痕迹可知DE是AC的垂直平分线,∴AD=CD,AC=2AE=4,∵△ABD的周长为15,∴AB+BD+AD=AB+BD+DC=AB+BC=15,∴△ABC的周长=AB+BC+AC=15+4=19.
5.解:作法如下:
(1)连接AB,AC,BC.
(2)作线段AB的垂直平分线EF.
(3)作线段AC的垂直平分线PQ,EF与PQ相交于M点,则M点即为中转站的位置,如图1所示.
理由如下:连接MA,MB,MC,如图2所示.
∵EF是AB的垂直平分线,
∴MA=MB.
∵PQ是AC的垂直平分线,
∴MA=MC.
∴MB=MC=MA.
∴中转站M到三个食品加工厂的距离相等.
6.解:(1)如图,线段AB即为所求,理由:两点之间,线段最短.
(2)如图,线段BC即为所求,理由:直线外一点与直线上各点连接的所有线段中,垂线段最短.
(3)AC7.B 解析:过点D作DH⊥AB于点H,如图.根据作图痕迹可知AD平分∠CAB,∵DC⊥AC,DH⊥AB,∴DC=DH,∵S△ABC=S△ADC+S△ADB,∴16=·AC·DC+·AB·DH=·DC·(AC+AB),解得DC=2.故选B.
8.A 解析:过点D作DE⊥AB于点E(图略),由作图痕迹可知,AD是∠BAC的平分线,又∵AC⊥BC,∴DE=CD=4,∴S△ABD=AB·DE=24.故选A.
9.4 解析:如图,过F作FF'⊥AB于点F',由作图痕迹得AF平分∠BAC,FG⊥AC,∴FG=FF',∵△ABC的面积为9,∴(AB+AC)FG=9,即(5+AC)×2=9,解得AC=4.
10.解:(1)如图1,点P即为所求.
(2)如图2,点E1,E2,E3即为所求.
11.解:(1)如图,射线BQ是∠ABC的平分线,直线MN是线段AB的垂直平分线.
(2)由题意,BQ与MN交于点F,设MN与AB相交于点D,如图.
∵BQ平分∠ABC,∴∠CBF=∠ABF,
∵点F在线段AB的垂直平分线MN上,
∴AF=BF,又∵AD=BD,FD=FD,∴△AFD≌△BFD(SSS),
∴∠ABF=∠BAF,
∴∠CBF=∠ABF=∠BAF,
∵∠ABC+∠BAC+∠ACB=180°,且∠ACB=60°,∠CAF=24°,
∴∠CBF+∠ABF+∠BAF+24°+60°=180°,
∴3∠BAF+24°+60°=180°,解得∠BAF=32°.
∴∠BAF的度数是32°.
与线段垂直平分线有关的尺规作图
1.观察图中尺规作图的痕迹,可知线段BD一定是 ( )
A.△ABC的角平分线
B.△ABC的中线
C.△ABC的高线
D.AC边的垂直平分线
2.观察下列作图痕迹,所作线段CD为△ABC的中线的是 ( )
3.如图,在△ABC中,AB=AC,BC=4,分别以点A,B为圆心,大于AB的长为半径作弧,两弧交于点E,F,过E,F两点作直线交AC于点D,连接BD,△BCD的周长是10,则AB长为 ( )
A.10 B.8 C.6 D.4
4.△ABC中直线DE的作图痕迹如图所示,直线DE与BC,AC的交点为D,E,若AE=2,△ABD的周长是15,则△ABC的周长为 .
5.(教材变式)如图所示,某地有三个相邻的食品加工厂A,B,C,现计划建一个食品中转站,使中转站到三个食品加工厂的距离相等,请你利用尺规作图的方法,确定中转站的位置并说明理由.
6.(2025邢台威县月考)如图,汽车站、码头分别位于A,B两点,直线m,n分别表示公路与河流.
(1)从汽车站A到码头B怎样走最近 利用尺规作图的方法画出最近路线,并说明理由.
(2)从码头B到公路m怎样走最近 画出最近路线BC,并说明理由.
(3)在(1)(2)的基础上,比较AC和AB的大小,并说明理由.
与角平分线有关的尺规作图
7.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,适当长为半径画弧,两弧交于点P,作射线AP交BC于点D,若△ABC的面积是16,AB+AC=16,则CD的长为 ( )
A.1 B.2 C.3 D.4
8.(2025昆明嵩明县期末)如图,在△ABC中,∠C=90°,以A为圆心,适当长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,适当长为半径画弧,两弧交于点P,连接AP并延长交BC于点D.若CD=4,AB=12,则S△ABD的值为 ( )
A.24 B.36 C.48 D.60
9.如图,在△ABC中,按以下步骤作图:①以点A为圆心,适当长为半径画弧,与边AB,AC分别交于点E,D;②分别以D,E为圆心,适当长为半径画弧,两弧在∠BAC内交于点M;③作射线AM,交BC于点F;④过点F作FG⊥AC,垂足为点G.若△ABC的面积为9,AB=5,FG=2,则AC的长为 .
10.(2025无锡滨湖区月考)在四边形ABCD中,仅用无刻度的直尺和圆规完成下列作图(不写作法,保留作图痕迹).
(1)如图1,在边AB上确定点P,使点P到边CD,CB的距离相等.
(2)如图2,在四边形ABCD的边上确定点E的位置,使∠A+∠BED=180°,若点E有不同位置,请用E1,E2…区分.(注:四边形的内角和等于360°)
与线段垂直平分线、角平分线都有关的尺规作图
11.(2025呼和浩特回民区期中)如图,在△ABC中,利用直尺和圆规完成下列作图.
(1)作∠ABC的平分线,线段AB的垂直平分线,保留作图痕迹.
(2)在(1)中,所作角平分线与垂直平分线相交于点F,连接AF,若∠ACB=60°,∠CAF=24°,则∠BAF的度数是多少
【详解答案】
1.C
2.B 解析:A.可得BC=BD,不符合题意;B.CD为△ABC的边AB上的中线,符合题意;C.CD是∠ACB的平分线,不符合题意;D.CD⊥AB,但不平分,不符合题意.故选B.
3.C 解析:由作图过程可知EF是线段AB的垂直平分线,∴AD=BD,∴△BCD的周长=BC+CD+BD=BC+CD+AD=BC+AC=4+AC=10,∴AC=6,∴AB=AC=6.故选C.
4.19 解析:根据作图痕迹可知DE是AC的垂直平分线,∴AD=CD,AC=2AE=4,∵△ABD的周长为15,∴AB+BD+AD=AB+BD+DC=AB+BC=15,∴△ABC的周长=AB+BC+AC=15+4=19.
5.解:作法如下:
(1)连接AB,AC,BC.
(2)作线段AB的垂直平分线EF.
(3)作线段AC的垂直平分线PQ,EF与PQ相交于M点,则M点即为中转站的位置,如图1所示.
理由如下:连接MA,MB,MC,如图2所示.
∵EF是AB的垂直平分线,
∴MA=MB.
∵PQ是AC的垂直平分线,
∴MA=MC.
∴MB=MC=MA.
∴中转站M到三个食品加工厂的距离相等.
6.解:(1)如图,线段AB即为所求,理由:两点之间,线段最短.
(2)如图,线段BC即为所求,理由:直线外一点与直线上各点连接的所有线段中,垂线段最短.
(3)AC
8.A 解析:过点D作DE⊥AB于点E(图略),由作图痕迹可知,AD是∠BAC的平分线,又∵AC⊥BC,∴DE=CD=4,∴S△ABD=AB·DE=24.故选A.
9.4 解析:如图,过F作FF'⊥AB于点F',由作图痕迹得AF平分∠BAC,FG⊥AC,∴FG=FF',∵△ABC的面积为9,∴(AB+AC)FG=9,即(5+AC)×2=9,解得AC=4.
10.解:(1)如图1,点P即为所求.
(2)如图2,点E1,E2,E3即为所求.
11.解:(1)如图,射线BQ是∠ABC的平分线,直线MN是线段AB的垂直平分线.
(2)由题意,BQ与MN交于点F,设MN与AB相交于点D,如图.
∵BQ平分∠ABC,∴∠CBF=∠ABF,
∵点F在线段AB的垂直平分线MN上,
∴AF=BF,又∵AD=BD,FD=FD,∴△AFD≌△BFD(SSS),
∴∠ABF=∠BAF,
∴∠CBF=∠ABF=∠BAF,
∵∠ABC+∠BAC+∠ACB=180°,且∠ACB=60°,∠CAF=24°,
∴∠CBF+∠ABF+∠BAF+24°+60°=180°,
∴3∠BAF+24°+60°=180°,解得∠BAF=32°.
∴∠BAF的度数是32°.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
