第十七章 特殊三角形 测试卷(含答案) 2025-2026学年数学冀教版(2024)八年级上册
文档属性
| 名称 | 第十七章 特殊三角形 测试卷(含答案) 2025-2026学年数学冀教版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 166.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 13:32:47 | ||
图片预览




文档简介
第十七章 特殊三角形 测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在等腰三角形ABC中,若∠A=70°,则∠B的度数是 ( )
A.40° B.55°
C.70° D.40°或55°或70°
2.在下列三角形中,是直角三角形的是 ( )
A.三角形的三边满足关系a+b=c
B.三角形的三边长分别为32,42,52
C.三角形的一边等于另一边的一半
D.三角形的三边长分别为7,24,25
3.(2025漳州龙海区月考)用反证法证明:a,b至少有一个是0,应该假设 ( )
A.a,b都不是0 B.a,b只有一个是0
C.a,b至多一个是0 D.a,b两个都是0
4.如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2 km.据此,可得学校与工厂之间的距离AB等于 ( )
A.2 km B.3 km C.2 km D.4 km
5.如图,点C,E在OA上,点D在OB上,且OC=CD=DE,若∠EDB=75°,则∠AOB= ( )
A.35° B.25° C.20° D.15°
6.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是 ( )
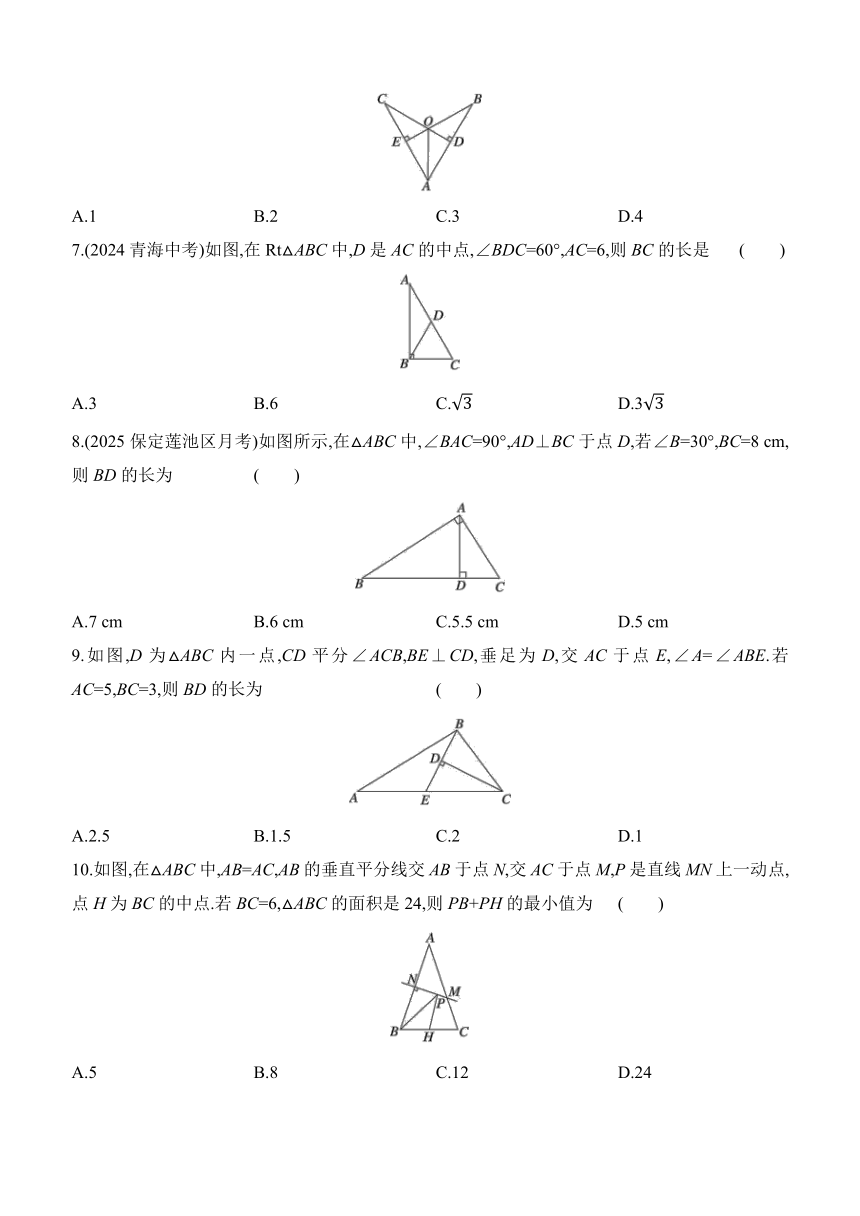
A.1 B.2 C.3 D.4
7.(2024青海中考)如图,在Rt△ABC中,D是AC的中点,∠BDC=60°,AC=6,则BC的长是 ( )
A.3 B.6 C. D.3
8.(2025保定莲池区月考)如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,若∠B=30°,BC=8 cm,则BD的长为 ( )
A.7 cm B.6 cm C.5.5 cm D.5 cm
9.如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE.若AC=5,BC=3,则BD的长为 ( )
A.2.5 B.1.5 C.2 D.1
10.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交AC于点M,P是直线MN上一动点,点H为BC的中点.若BC=6,△ABC的面积是24,则PB+PH的最小值为 ( )
A.5 B.8 C.12 D.24
11.如图,3×3网格由9个边长为1的小正方形组成,以点B为圆心,AB长为半径画圆弧交数轴于点A',则点A'表示的实数为 ( )
A.- B. C.-2 D.-+1
12.《周髀算经》中记载了“勾三股四弦五”的直角三角形边长关系,即当直角三角形的两条直角边长分别为3和4时,斜边长为5.受此启发,我们定义:若一个直角三角形的两条直角边a和b满足=k(k为正实数),则称这个直角三角形为“勾股标准形”直角三角形.现有一个“勾股标准形”直角三角形,若其面积为24,则它的斜边长是 ( )
A.5 B.5 C.10 D.10
二、填空题(本大题共4个小题,每小题3分,共12分)
13.已知一等腰三角形的一个内角为80°,则这个等腰三角形顶角的度数为 .
14.(2024绥化中考)如图,AB∥CD,∠C=33°,OC=OE,则∠A= °.
15.如图,在△ABC中,点D在边BC上,AB=AD,E,F分别是AC,BD的中点,EF=3,则AC的长为 .
16.如图所示的是某超市购物车的侧面简化示意图.测得支架AC=24 cm,CB=18 cm,两轮中心的距离AB=30 cm,则点C到AB的距离为 cm.
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)如图,AB∥CD,直线MN与AB,CD分别交于点E,F,CD上有一点G且GE=GF,∠1=122°,求∠2的度数.
18.(8分)如图,在△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于点E,已知∠ABE=40°,求∠EBC的度数.
19.(8分)如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数.
(2)求证:FB=FE.
20.(8分)(2025石家庄高邑县月考)如图,DE⊥AB于点E,DF⊥AC于点F,若BD=CD,BE=CF.
求证:AD平分∠BAC.
21.(8分)如图,在△ABC中,AB=AC,点D为AC上一点,且满足AD=BD=BC.点F在BC延长线上,连接FD并延长,交AB于点E,连接AF.
(1)求∠BAC和∠ACB的度数.
(2)若点E是AB的中点,求证:△ABF是等腰三角形.
22.(10分)如图,在△ABC中,∠C=90°,点P,D分别在AC,AB上,且PD=PA,BD的垂直平分线交BC于点E,交BD于点F,连接PE,DE.
(1)求证:DE⊥PD.
(2)若AC=10,BC=12,PA=3,求线段DE的长.
23.(10分)台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300 km和400 km,又AB=500 km,以台风中心为圆心周围250 km以内为受影响区域.
(1)海港C受台风影响吗 为什么
(2)若台风的速度为20 km/h,台风影响该海港持续的时间有多长
24.(12分)如图,O是等边三角形ABC内一点.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.已知∠AOB=110°.
(1)求证:△COD是等边三角形.
(2)当α=150°时,试判断△AOD的形状,并说明理由.
(3)探究:当α为多少度时,△AOD是等腰三角形
【详解答案】
1.D 解析:等腰三角形ABC中,已知∠A=70°,分两种情况讨论:①∠A为底角,那另外两个角为70°和40°;②∠A为顶角,那另外两个角都为55°.所以∠B的度数是70°或55°或40°.故选D.
2.D 解析:∵72+242=252,∴以7,24,25为三边长的三角形是直角三角形.故选D.
3.A 解析:由于命题:“a,b至少有一个为0”的反面是:“a,b都不是0”,故用反证法证明:“a,b至少有一个为0”,应假设“a,b都不是0”.故选A.
4.D 解析:∵∠A=60°,∠C=90°,AC=2 km,∴∠B=30°.∴AB=2AC=4 km.故选D.
5.B 解析:∵OC=CD,∴∠O=∠CDO.∵∠DCE是△OCD的一个外角,∴∠DCE=∠O+∠CDO=2∠O.∵CD=DE,∴∠DEC=∠DCE=2∠O.∵∠EDB是△EOD的一个外角,∴∠EDB=∠O+∠DEC=3∠O.∵∠EDB=75°,∴∠O=25°,即∠AOB=25°.故选B.
6.C 解析:∵CD⊥AB,BE⊥AC,∴∠ADC=∠AEB=90°.在△ADC和△AEB中,
∴△ADC≌△AEB(AAS).∴AD=AE,∠C=∠B.∵AB=AC,∴BD=CE.在△BOD和△COE中,
∴△BOD≌△COE(AAS).∴OB=OC,OD=OE.在Rt△ADO和Rt△AEO中,∴Rt△ADO≌Rt△AEO(HL).∴共有3对全等的直角三角形.故选C.
7.A 解析:∵点D是Rt△ABC斜边AC的中点,AC=6,∴BD=CD=AD=AC=3,∵∠BDC=60°,∴△BCD为等边三角形,∴BC=BD=3.故选A.
8.B 解析:∵∠BAC=90°,∠B=30°,∴∠C=90°-∠B=60°,∵AD⊥BC于点D,∠C=60°,∴∠DAC=30°,∴在Rt△ABC中,AC=BC=4 cm,∴Rt△ACD中,∠DAC=30°,∴CD=AC=2 cm,∴BD=BC-CD=8-2=6(cm).故选B.
9.D 解析:∵CD平分∠ACB,CD⊥BE,∠CDB=∠CDE,CD=CD,∠BCD=∠ECD,∴△BCD≌△ECD,∴BC=CE.又∵∠A=∠ABE,∴AE=BE.∴BD=BE=AE=(AC-BC).∵AC=5,BC=3,∴BD=×(5-3)=1.故选D.
10.B 解析:如图所示,连接AP,AH,由题意可得PB=PA,∴PB+PH=PA+PH,∵PA+PH≥AH,∴当点A,P,H在一条直线上时,PA+PH的值最小,即PB+PH的值最小,∵AB=AC,H是BC的中点,∴AH⊥BC,∴S△ABC=BC·AH=24,解得AH=8.故选B.
11.A 解析:由勾股定理得AB=,∵以点B为圆心,AB长为半径画圆弧交数轴于点A',∴A'B=AB=,∵点A'在负半轴上,∴点A'表示的实数为-.故选A.
12.C 解析:由题意可知a=3k,b=4k,∴S=ab=×3k×4k=24,解得k=2,∴a=6,b=8,∴斜边长为=10.故选C.
13.20°或80° 解析:(1)若等腰三角形的一个底角为80°,则顶角为180°-80°-80°=20°;(2)等腰三角形的顶角为80°.因此,这个等腰三角形的顶角的度数为20°或80°.
14.66 解析:∵OC=OE,∠C=33°,∴∠E=∠C=33°,∴∠DOE=∠E+∠C=66°,∵AB∥CD,∴∠A=∠DOE=66°.
15.6 解析:如图,连接AF.∵AB=AD,F为BD的中点,∴AF⊥BD,即∠AFC=90°.∵E为AC的中点,∴EF=AC.∵EF=3,∴AC=6.
16. 解析:连接AB,过C作CD⊥AB于点D,如图所示,∵AC=24 cm,CB=18 cm,AB=30 cm,∴AC2+BC2=AB2,∴△ABC是直角三角形,∵△ABC的面积=AC·BC=AB·CD,即24×18=30·CD,解得CD= cm,即点C到AB的距离为 cm.
17.解:∵AB∥CD,
∴∠MFD=∠1=122°.
∵GE=GF,
∴∠GFE=∠GEF=180°-∠MFD=180°-122°=58°.
∴∠2=180°-58°-58°=64°.
18.解:∵DE是AB的垂直平分线,
∴AE=BE,
∴∠A=∠ABE,
∵∠ABE=40°,
∴∠A=40°,
∵AB=AC,
∴∠ABC=∠C=(180°-∠A)=70°,
∴∠EBC=∠ABC-∠ABE=70°-40°=30°.
19.解:(1)∵AB=AC,
∴∠C=∠ABC.
∵∠C=36°,
∴∠ABC=36°.
∵BD=CD,AB=AC,
∴AD⊥BC.
∴∠ADB=90°.
∴∠BAD=90°-36°=54°.
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE=∠ABC.
∵EF∥BC,
∴∠FEB=∠CBE.
∴∠ABE=∠FEB.
∴FB=FE.
20.证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF,
在Rt△ADE与Rt△ADF中,
∴Rt△ADE≌Rt△ADF(HL),
∴∠DAE=∠DAF,
∴AD平分∠BAC.
21.解:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵AD=BD=BC,
∴∠BAD=∠ABD,∠BCD=∠BDC,
∵∠BDC=∠BAC+∠ABD=2∠BAC,
∴∠ABC=∠ACB=2∠BAC,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠BAC+2∠BAC+2∠BAC=180°,
∴∠BAC=36°,∠ACB=2∠BAC=72°.
(2)证明:∵AD=BD,E是AB的中点,
∴DE垂直平分AB,
∴FA=FB,
∴△ABF是等腰三角形.
22.解:(1)证明:∵PD=PA,∴∠PDA=∠A.∵EF垂直平分BD,∴ED=EB,∴∠EDB=∠B.在Rt△ABC中,∠ACB=90°,∴∠A+∠B=90°,∴∠PDA+∠EDB=90°,∴∠PDE=90°,∴DE⊥PD.
(2)∵AC=10,BC=12,PA=3,∴CP=AC-PA=7,PD=PA=3.设DE=BE=x,则CE=12-x.在Rt△PEC中,根据勾股定理,得PE2=PC2+CE2=72+(12-x)2,在Rt△PDE中,根据勾股定理,得PE2=PD2+DE2=32+x2,∴72+(12-x)2=32+x2,解得x=,∴DE=.
23.解:(1)海港C受台风影响.
理由:如图,过点C作CD⊥AB于点D,
∵AC=300 km,BC=400 km,AB=500 km,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
∴AC·BC=CD·AB,即300×400=500·CD,解得CD=240 km.
∵240 km<250 km,
∴海港C受台风影响.
(2)设台风到达点E时开始影响该海港,到达点F时解除影响该海港,
则EC=250 km,FC=250 km.
∴ED==70(km),
∵CD⊥AB于点D,
∴EF=2ED=140 km.
∵台风的速度为20 km/h,
∴140÷20=7(h).
∴台风影响该海港持续的时间为7 h.
24.解:(1)证明:∵△BOC绕点C按顺时针方向旋转60°得到△ADC,
∴CO=CD,∠OCD=60°.
∴△COD是等边三角形.
(2)当α=150°时,
△AOD是直角三角形.
理由如下:∵△BOC≌△ADC,
∴∠ADC=∠BOC=150°.
又∵△COD是等边三角形,
∴∠ODC=60°.
∴∠ADO=150°-60°=90°,
即△AOD是直角三角形.
(3)①要使AO=AD,需∠AOD=∠ADO.
∵∠AOD=360°-∠AOB-∠COD-α=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°.
∴α=125°.
②要使OA=OD,需∠OAD=∠ADO.
∵∠AOD=190°-α,∠ADO=α-60°,
∴∠OAD=180°-(∠AOD+∠ADO)=50°.
∴α-60°=50°.
∴α=110°.
③要使OD=AD,需∠OAD=∠AOD.
∴190°-α=50°.
∴α=140°.
综上所述,当α的度数为125°或110°或140°时,△AOD是等腰三角形.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在等腰三角形ABC中,若∠A=70°,则∠B的度数是 ( )
A.40° B.55°
C.70° D.40°或55°或70°
2.在下列三角形中,是直角三角形的是 ( )
A.三角形的三边满足关系a+b=c
B.三角形的三边长分别为32,42,52
C.三角形的一边等于另一边的一半
D.三角形的三边长分别为7,24,25
3.(2025漳州龙海区月考)用反证法证明:a,b至少有一个是0,应该假设 ( )
A.a,b都不是0 B.a,b只有一个是0
C.a,b至多一个是0 D.a,b两个都是0
4.如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2 km.据此,可得学校与工厂之间的距离AB等于 ( )
A.2 km B.3 km C.2 km D.4 km
5.如图,点C,E在OA上,点D在OB上,且OC=CD=DE,若∠EDB=75°,则∠AOB= ( )
A.35° B.25° C.20° D.15°
6.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是 ( )
A.1 B.2 C.3 D.4
7.(2024青海中考)如图,在Rt△ABC中,D是AC的中点,∠BDC=60°,AC=6,则BC的长是 ( )
A.3 B.6 C. D.3
8.(2025保定莲池区月考)如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,若∠B=30°,BC=8 cm,则BD的长为 ( )
A.7 cm B.6 cm C.5.5 cm D.5 cm
9.如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE.若AC=5,BC=3,则BD的长为 ( )
A.2.5 B.1.5 C.2 D.1
10.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交AC于点M,P是直线MN上一动点,点H为BC的中点.若BC=6,△ABC的面积是24,则PB+PH的最小值为 ( )
A.5 B.8 C.12 D.24
11.如图,3×3网格由9个边长为1的小正方形组成,以点B为圆心,AB长为半径画圆弧交数轴于点A',则点A'表示的实数为 ( )
A.- B. C.-2 D.-+1
12.《周髀算经》中记载了“勾三股四弦五”的直角三角形边长关系,即当直角三角形的两条直角边长分别为3和4时,斜边长为5.受此启发,我们定义:若一个直角三角形的两条直角边a和b满足=k(k为正实数),则称这个直角三角形为“勾股标准形”直角三角形.现有一个“勾股标准形”直角三角形,若其面积为24,则它的斜边长是 ( )
A.5 B.5 C.10 D.10
二、填空题(本大题共4个小题,每小题3分,共12分)
13.已知一等腰三角形的一个内角为80°,则这个等腰三角形顶角的度数为 .
14.(2024绥化中考)如图,AB∥CD,∠C=33°,OC=OE,则∠A= °.
15.如图,在△ABC中,点D在边BC上,AB=AD,E,F分别是AC,BD的中点,EF=3,则AC的长为 .
16.如图所示的是某超市购物车的侧面简化示意图.测得支架AC=24 cm,CB=18 cm,两轮中心的距离AB=30 cm,则点C到AB的距离为 cm.
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)如图,AB∥CD,直线MN与AB,CD分别交于点E,F,CD上有一点G且GE=GF,∠1=122°,求∠2的度数.
18.(8分)如图,在△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于点E,已知∠ABE=40°,求∠EBC的度数.
19.(8分)如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数.
(2)求证:FB=FE.
20.(8分)(2025石家庄高邑县月考)如图,DE⊥AB于点E,DF⊥AC于点F,若BD=CD,BE=CF.
求证:AD平分∠BAC.
21.(8分)如图,在△ABC中,AB=AC,点D为AC上一点,且满足AD=BD=BC.点F在BC延长线上,连接FD并延长,交AB于点E,连接AF.
(1)求∠BAC和∠ACB的度数.
(2)若点E是AB的中点,求证:△ABF是等腰三角形.
22.(10分)如图,在△ABC中,∠C=90°,点P,D分别在AC,AB上,且PD=PA,BD的垂直平分线交BC于点E,交BD于点F,连接PE,DE.
(1)求证:DE⊥PD.
(2)若AC=10,BC=12,PA=3,求线段DE的长.
23.(10分)台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300 km和400 km,又AB=500 km,以台风中心为圆心周围250 km以内为受影响区域.
(1)海港C受台风影响吗 为什么
(2)若台风的速度为20 km/h,台风影响该海港持续的时间有多长
24.(12分)如图,O是等边三角形ABC内一点.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.已知∠AOB=110°.
(1)求证:△COD是等边三角形.
(2)当α=150°时,试判断△AOD的形状,并说明理由.
(3)探究:当α为多少度时,△AOD是等腰三角形
【详解答案】
1.D 解析:等腰三角形ABC中,已知∠A=70°,分两种情况讨论:①∠A为底角,那另外两个角为70°和40°;②∠A为顶角,那另外两个角都为55°.所以∠B的度数是70°或55°或40°.故选D.
2.D 解析:∵72+242=252,∴以7,24,25为三边长的三角形是直角三角形.故选D.
3.A 解析:由于命题:“a,b至少有一个为0”的反面是:“a,b都不是0”,故用反证法证明:“a,b至少有一个为0”,应假设“a,b都不是0”.故选A.
4.D 解析:∵∠A=60°,∠C=90°,AC=2 km,∴∠B=30°.∴AB=2AC=4 km.故选D.
5.B 解析:∵OC=CD,∴∠O=∠CDO.∵∠DCE是△OCD的一个外角,∴∠DCE=∠O+∠CDO=2∠O.∵CD=DE,∴∠DEC=∠DCE=2∠O.∵∠EDB是△EOD的一个外角,∴∠EDB=∠O+∠DEC=3∠O.∵∠EDB=75°,∴∠O=25°,即∠AOB=25°.故选B.
6.C 解析:∵CD⊥AB,BE⊥AC,∴∠ADC=∠AEB=90°.在△ADC和△AEB中,
∴△ADC≌△AEB(AAS).∴AD=AE,∠C=∠B.∵AB=AC,∴BD=CE.在△BOD和△COE中,
∴△BOD≌△COE(AAS).∴OB=OC,OD=OE.在Rt△ADO和Rt△AEO中,∴Rt△ADO≌Rt△AEO(HL).∴共有3对全等的直角三角形.故选C.
7.A 解析:∵点D是Rt△ABC斜边AC的中点,AC=6,∴BD=CD=AD=AC=3,∵∠BDC=60°,∴△BCD为等边三角形,∴BC=BD=3.故选A.
8.B 解析:∵∠BAC=90°,∠B=30°,∴∠C=90°-∠B=60°,∵AD⊥BC于点D,∠C=60°,∴∠DAC=30°,∴在Rt△ABC中,AC=BC=4 cm,∴Rt△ACD中,∠DAC=30°,∴CD=AC=2 cm,∴BD=BC-CD=8-2=6(cm).故选B.
9.D 解析:∵CD平分∠ACB,CD⊥BE,∠CDB=∠CDE,CD=CD,∠BCD=∠ECD,∴△BCD≌△ECD,∴BC=CE.又∵∠A=∠ABE,∴AE=BE.∴BD=BE=AE=(AC-BC).∵AC=5,BC=3,∴BD=×(5-3)=1.故选D.
10.B 解析:如图所示,连接AP,AH,由题意可得PB=PA,∴PB+PH=PA+PH,∵PA+PH≥AH,∴当点A,P,H在一条直线上时,PA+PH的值最小,即PB+PH的值最小,∵AB=AC,H是BC的中点,∴AH⊥BC,∴S△ABC=BC·AH=24,解得AH=8.故选B.
11.A 解析:由勾股定理得AB=,∵以点B为圆心,AB长为半径画圆弧交数轴于点A',∴A'B=AB=,∵点A'在负半轴上,∴点A'表示的实数为-.故选A.
12.C 解析:由题意可知a=3k,b=4k,∴S=ab=×3k×4k=24,解得k=2,∴a=6,b=8,∴斜边长为=10.故选C.
13.20°或80° 解析:(1)若等腰三角形的一个底角为80°,则顶角为180°-80°-80°=20°;(2)等腰三角形的顶角为80°.因此,这个等腰三角形的顶角的度数为20°或80°.
14.66 解析:∵OC=OE,∠C=33°,∴∠E=∠C=33°,∴∠DOE=∠E+∠C=66°,∵AB∥CD,∴∠A=∠DOE=66°.
15.6 解析:如图,连接AF.∵AB=AD,F为BD的中点,∴AF⊥BD,即∠AFC=90°.∵E为AC的中点,∴EF=AC.∵EF=3,∴AC=6.
16. 解析:连接AB,过C作CD⊥AB于点D,如图所示,∵AC=24 cm,CB=18 cm,AB=30 cm,∴AC2+BC2=AB2,∴△ABC是直角三角形,∵△ABC的面积=AC·BC=AB·CD,即24×18=30·CD,解得CD= cm,即点C到AB的距离为 cm.
17.解:∵AB∥CD,
∴∠MFD=∠1=122°.
∵GE=GF,
∴∠GFE=∠GEF=180°-∠MFD=180°-122°=58°.
∴∠2=180°-58°-58°=64°.
18.解:∵DE是AB的垂直平分线,
∴AE=BE,
∴∠A=∠ABE,
∵∠ABE=40°,
∴∠A=40°,
∵AB=AC,
∴∠ABC=∠C=(180°-∠A)=70°,
∴∠EBC=∠ABC-∠ABE=70°-40°=30°.
19.解:(1)∵AB=AC,
∴∠C=∠ABC.
∵∠C=36°,
∴∠ABC=36°.
∵BD=CD,AB=AC,
∴AD⊥BC.
∴∠ADB=90°.
∴∠BAD=90°-36°=54°.
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE=∠ABC.
∵EF∥BC,
∴∠FEB=∠CBE.
∴∠ABE=∠FEB.
∴FB=FE.
20.证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF,
在Rt△ADE与Rt△ADF中,
∴Rt△ADE≌Rt△ADF(HL),
∴∠DAE=∠DAF,
∴AD平分∠BAC.
21.解:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵AD=BD=BC,
∴∠BAD=∠ABD,∠BCD=∠BDC,
∵∠BDC=∠BAC+∠ABD=2∠BAC,
∴∠ABC=∠ACB=2∠BAC,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠BAC+2∠BAC+2∠BAC=180°,
∴∠BAC=36°,∠ACB=2∠BAC=72°.
(2)证明:∵AD=BD,E是AB的中点,
∴DE垂直平分AB,
∴FA=FB,
∴△ABF是等腰三角形.
22.解:(1)证明:∵PD=PA,∴∠PDA=∠A.∵EF垂直平分BD,∴ED=EB,∴∠EDB=∠B.在Rt△ABC中,∠ACB=90°,∴∠A+∠B=90°,∴∠PDA+∠EDB=90°,∴∠PDE=90°,∴DE⊥PD.
(2)∵AC=10,BC=12,PA=3,∴CP=AC-PA=7,PD=PA=3.设DE=BE=x,则CE=12-x.在Rt△PEC中,根据勾股定理,得PE2=PC2+CE2=72+(12-x)2,在Rt△PDE中,根据勾股定理,得PE2=PD2+DE2=32+x2,∴72+(12-x)2=32+x2,解得x=,∴DE=.
23.解:(1)海港C受台风影响.
理由:如图,过点C作CD⊥AB于点D,
∵AC=300 km,BC=400 km,AB=500 km,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
∴AC·BC=CD·AB,即300×400=500·CD,解得CD=240 km.
∵240 km<250 km,
∴海港C受台风影响.
(2)设台风到达点E时开始影响该海港,到达点F时解除影响该海港,
则EC=250 km,FC=250 km.
∴ED==70(km),
∵CD⊥AB于点D,
∴EF=2ED=140 km.
∵台风的速度为20 km/h,
∴140÷20=7(h).
∴台风影响该海港持续的时间为7 h.
24.解:(1)证明:∵△BOC绕点C按顺时针方向旋转60°得到△ADC,
∴CO=CD,∠OCD=60°.
∴△COD是等边三角形.
(2)当α=150°时,
△AOD是直角三角形.
理由如下:∵△BOC≌△ADC,
∴∠ADC=∠BOC=150°.
又∵△COD是等边三角形,
∴∠ODC=60°.
∴∠ADO=150°-60°=90°,
即△AOD是直角三角形.
(3)①要使AO=AD,需∠AOD=∠ADO.
∵∠AOD=360°-∠AOB-∠COD-α=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°.
∴α=125°.
②要使OA=OD,需∠OAD=∠ADO.
∵∠AOD=190°-α,∠ADO=α-60°,
∴∠OAD=180°-(∠AOD+∠ADO)=50°.
∴α-60°=50°.
∴α=110°.
③要使OD=AD,需∠OAD=∠AOD.
∴190°-α=50°.
∴α=140°.
综上所述,当α的度数为125°或110°或140°时,△AOD是等腰三角形.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
