数学九下《直线和圆的位置关系》ppt课件(共12张幻灯片)
文档属性
| 名称 | 数学九下《直线和圆的位置关系》ppt课件(共12张幻灯片) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-23 00:00:00 | ||
图片预览



文档简介
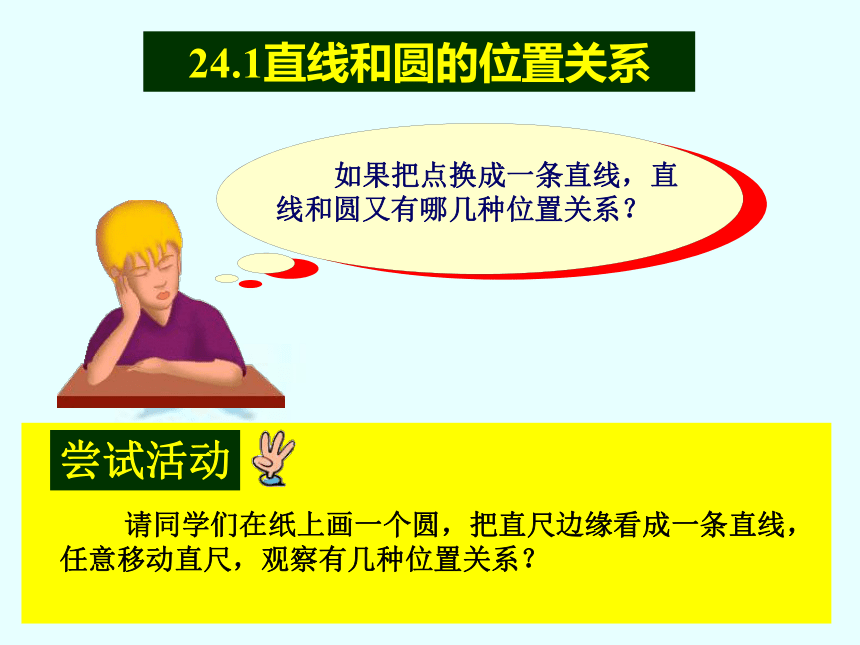
课件12张PPT。点和圆的位置关系点B在圆上点A在圆内点C在圆外数量特征 还记得巴金的《海上日出》吧,随着作家
的描写,我们领略到海上日出的壮丽景象.实
际上,日出是一个不断变化的动态过程,如果
把太阳(透视图)看作一个圆,把海平面(透视图)看作一条直线,太阳升起的过程中与海平面的位置关系就是直线与圆的位置关系的最好例证. 还记得巴金的《海上日出》吧,随着作家
的描写,我们领略到海上日出的壮丽景象.实
际上,日出是一个不断变化的动态过程,如果
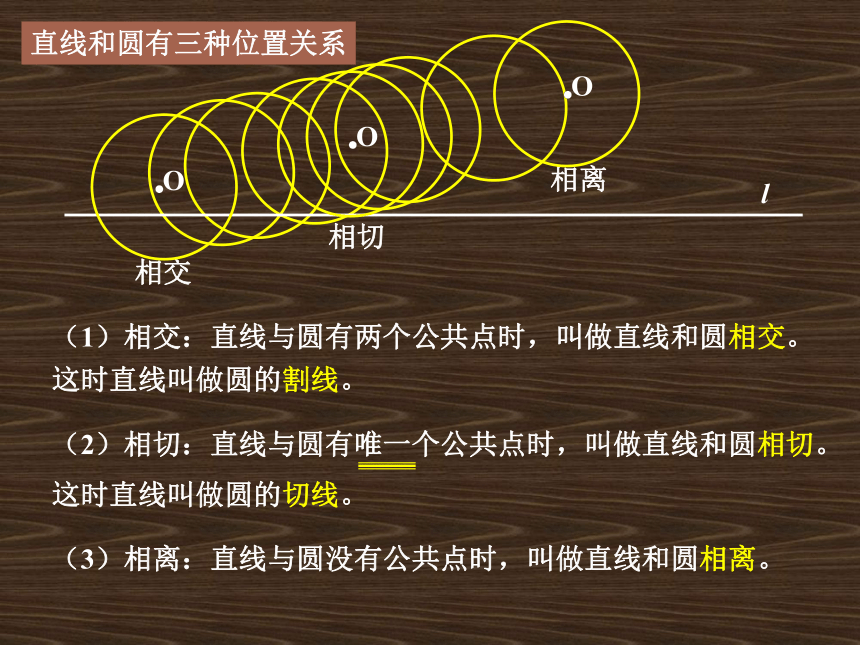
把太阳(透视图)看作一个圆,把海平面(透视图)看作一条直线,太阳升起的过程中与海平面的位置关系就是直线与圆的位置关系的最好例证. 如果把点换成一条直线,直
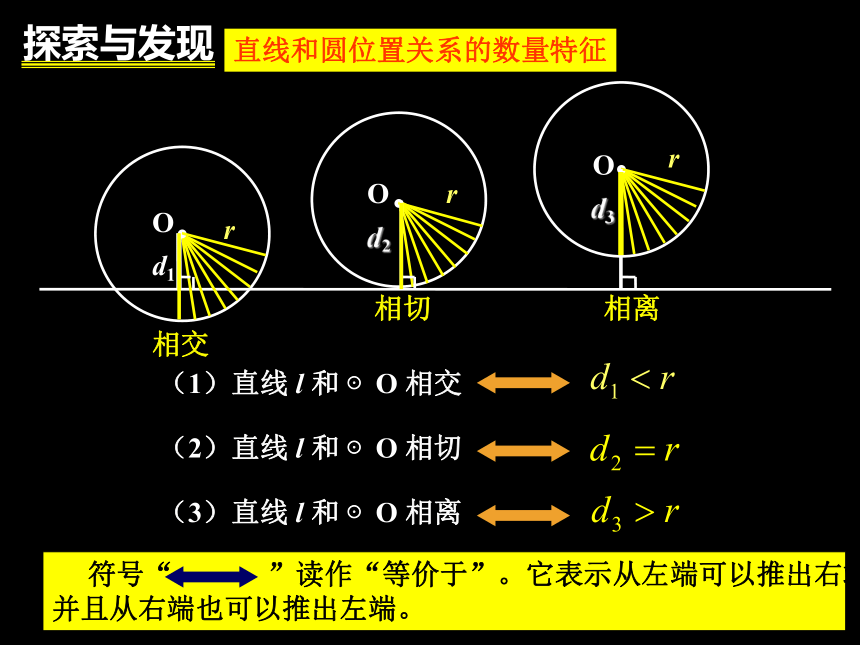
线和圆又有哪几种位置关系?24.1直线和圆的位置关系相交相切相离直线和圆有三种位置关系(1)相交:直线与圆有两个公共点时,叫做直线和圆相交。这时直线叫做圆的割线。(2)相切:直线与圆有唯一个公共点时,叫做直线和圆相切。这时直线叫做圆的切线。(3)相离:直线与圆没有公共点时,叫做直线和圆相离。直线和圆位置关系的数量特征相交相切相离OOO探索与发现 已知圆的直径为13cm,如果直线和圆心的距离为:
(1) d =4.5cm 时,直线与圆的位置关系是 ,有 个交点;
(2) d =6.5cm时,直线与圆的位置关系是 ,有 个交点;
(3) d =8cm时,直线与圆的位置关系是 ,有 个交点。 练习1:6.5相交相切相离两一0例在 Rt△ABC 中,∠C = 90°,AC = 3 cm , BC = 4 cm , 以 C 为圆心,r 为半径的圆与 AB 有怎样的关系?为什么?(1)r = 2 cm ; (2) r = 2.4 cm ; (3) r = 3 cm .ACB解:过 C 作 CD⊥AB 于 D,在 Rt △ABC 中,根据三角形面积公式有CD · AB = AC · BC即圆心 C 到 AB 的距离 d = 2.4 cm.(1)当 r = 2 cm 时,有 d > r ,因此⊙O 和 AB 相离. (2)当 r = 2.4 cm 时,有 d = r ,因此⊙O 和 AB 相切. (3)当 r = 3 cm 时,有 d < r ,因此⊙O 和 AB 相交. 在 Rt△ABC 中,∠C = 90°,AC = 3 , AB = 5 , 以 C 为圆心,r 为半径作圆,那么:(1)直线AB与⊙ C相离时, r 的取值范围是 ;(2)直线AB与⊙ C相切时, r 的取值范围是 ;(3)直线AB与⊙ C相交时, r 的取值范围是 ;ACBD 当圆心到直线的距离一定时,圆与直线的位置关系由这个圆的半
径大小确定。练习2: 如图,已知∠AOB=300,M为OB上一点,且OM=5cm,以M为圆心,以 r 为半径的圆与直线OA有怎样的位置关系?为什么?
(1) r =2cm;
(2) r =4cm;
(3) r =2.5cm。AOB练习3:M∴MN= ×OM= ×5= 2.5cm解 : 过M作MN⊥OA于N∵ ∠AOB=300(1)当 r = 2cm 时, r <d,因此⊙M与OA相离。即圆心M到直线OA的距离是d=2.5cm .(2)当 r = 4cm 时, r >d ,因此⊙M与OA相交。(3)当 r = 2.5cm 时, r =d ,因此⊙M与OA相切。无切线割线无切点交点
d > r
d = r
02相切相交小结2、本节课利用
(1)类比点与圆的位置关系,从运动变化的观点来研究直线和圆的位置关系;(2)利用了分类的思想把直线和圆的位置关系分为三类讨论;(3)用了数形结合的思想,通过 d 与 r 这两个数量之间的关系
来研究直线和圆的位置关系。在解决直线和圆的位置关系时,应充分利用数形结合和分类讨论的思想.运用数形结合时要注意作图的准确性,分类讨论时要做到不重不漏.作业1、课本 第 3 题;2、等边三角形ABC的边长为 ,以A为圆心的圆与BC
所在的直线 l 有: (1)没有公共点;(2)唯一的公共点;(3)有两个公共点。求这三种情况下⊙A的半径 r 的范围。
的描写,我们领略到海上日出的壮丽景象.实
际上,日出是一个不断变化的动态过程,如果
把太阳(透视图)看作一个圆,把海平面(透视图)看作一条直线,太阳升起的过程中与海平面的位置关系就是直线与圆的位置关系的最好例证. 还记得巴金的《海上日出》吧,随着作家
的描写,我们领略到海上日出的壮丽景象.实
际上,日出是一个不断变化的动态过程,如果
把太阳(透视图)看作一个圆,把海平面(透视图)看作一条直线,太阳升起的过程中与海平面的位置关系就是直线与圆的位置关系的最好例证. 如果把点换成一条直线,直
线和圆又有哪几种位置关系?24.1直线和圆的位置关系相交相切相离直线和圆有三种位置关系(1)相交:直线与圆有两个公共点时,叫做直线和圆相交。这时直线叫做圆的割线。(2)相切:直线与圆有唯一个公共点时,叫做直线和圆相切。这时直线叫做圆的切线。(3)相离:直线与圆没有公共点时,叫做直线和圆相离。直线和圆位置关系的数量特征相交相切相离OOO探索与发现 已知圆的直径为13cm,如果直线和圆心的距离为:
(1) d =4.5cm 时,直线与圆的位置关系是 ,有 个交点;
(2) d =6.5cm时,直线与圆的位置关系是 ,有 个交点;
(3) d =8cm时,直线与圆的位置关系是 ,有 个交点。 练习1:6.5相交相切相离两一0例在 Rt△ABC 中,∠C = 90°,AC = 3 cm , BC = 4 cm , 以 C 为圆心,r 为半径的圆与 AB 有怎样的关系?为什么?(1)r = 2 cm ; (2) r = 2.4 cm ; (3) r = 3 cm .ACB解:过 C 作 CD⊥AB 于 D,在 Rt △ABC 中,根据三角形面积公式有CD · AB = AC · BC即圆心 C 到 AB 的距离 d = 2.4 cm.(1)当 r = 2 cm 时,有 d > r ,因此⊙O 和 AB 相离. (2)当 r = 2.4 cm 时,有 d = r ,因此⊙O 和 AB 相切. (3)当 r = 3 cm 时,有 d < r ,因此⊙O 和 AB 相交. 在 Rt△ABC 中,∠C = 90°,AC = 3 , AB = 5 , 以 C 为圆心,r 为半径作圆,那么:(1)直线AB与⊙ C相离时, r 的取值范围是 ;(2)直线AB与⊙ C相切时, r 的取值范围是 ;(3)直线AB与⊙ C相交时, r 的取值范围是 ;ACBD 当圆心到直线的距离一定时,圆与直线的位置关系由这个圆的半
径大小确定。练习2: 如图,已知∠AOB=300,M为OB上一点,且OM=5cm,以M为圆心,以 r 为半径的圆与直线OA有怎样的位置关系?为什么?
(1) r =2cm;
(2) r =4cm;
(3) r =2.5cm。AOB练习3:M∴MN= ×OM= ×5= 2.5cm解 : 过M作MN⊥OA于N∵ ∠AOB=300(1)当 r = 2cm 时, r <d,因此⊙M与OA相离。即圆心M到直线OA的距离是d=2.5cm .(2)当 r = 4cm 时, r >d ,因此⊙M与OA相交。(3)当 r = 2.5cm 时, r =d ,因此⊙M与OA相切。无切线割线无切点交点
d > r
d = r
02相切相交小结2、本节课利用
(1)类比点与圆的位置关系,从运动变化的观点来研究直线和圆的位置关系;(2)利用了分类的思想把直线和圆的位置关系分为三类讨论;(3)用了数形结合的思想,通过 d 与 r 这两个数量之间的关系
来研究直线和圆的位置关系。在解决直线和圆的位置关系时,应充分利用数形结合和分类讨论的思想.运用数形结合时要注意作图的准确性,分类讨论时要做到不重不漏.作业1、课本 第 3 题;2、等边三角形ABC的边长为 ,以A为圆心的圆与BC
所在的直线 l 有: (1)没有公共点;(2)唯一的公共点;(3)有两个公共点。求这三种情况下⊙A的半径 r 的范围。
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
