《勾股定理的逆定理》课件(共15张幻灯片)
文档属性
| 名称 | 《勾股定理的逆定理》课件(共15张幻灯片) |

|
|
| 格式 | zip | ||
| 文件大小 | 219.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-23 00:00:00 | ||
图片预览






文档简介
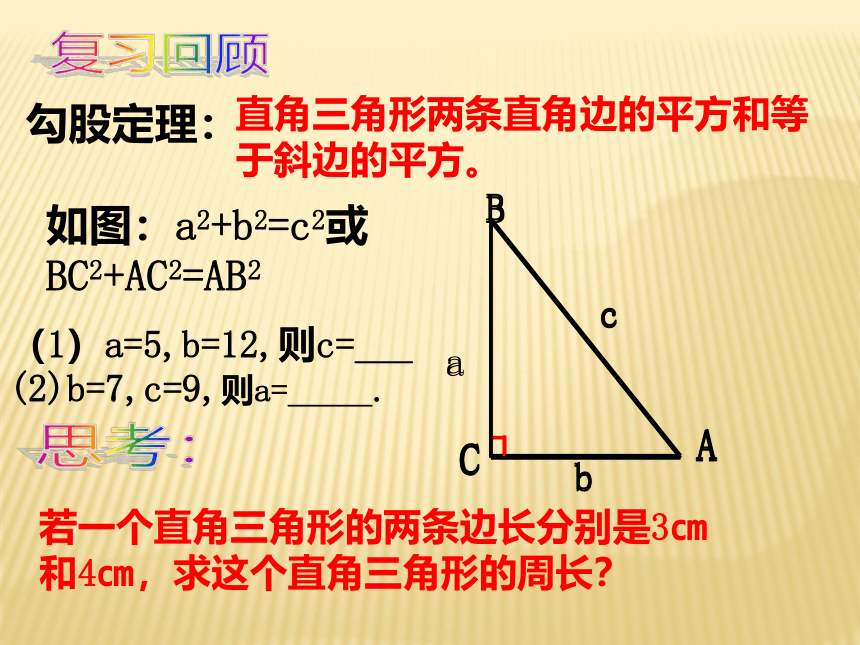
课件15张PPT。勾股定理的逆定理复习回顾勾股定理:直角三角形两条直角边的平方和等于斜边的平方。acbBCA如图:a2+b2=c2或BC2+AC2=AB2(1)a=5,b=12,则c=___
(2)b=7,c=9,则a=_____.思考:若一个直角三角形的两条边长分别是3㎝和4㎝,求这个直角三角形的周长?古埃及人曾用下面的方法得到直角:
他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形。其直角在第4个结处。他们真的能够得到直角三角形吗?我们也来试一试合作学习(1)画三个三角形,使其边长分别为3㎝,4㎝,5㎝;5㎝,12㎝,13㎝;8㎝,15㎝,17㎝(2)算一算较短两条边长的平方和与最长一条边长的平方是否相等?(3)用量角器量一量,它们都是什么三角形?由此,你能得到怎样的猜想?如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。勾股定理的逆定理(1)上述结论中,哪条边所对的角是直角?
(2)如果三角形中较短两边的平方和不等于
最长的平方,那么这个三角形是直角三角形吗?想一想:例1.根据下列条件,分别判断以a,b,c
为边的三角形是不是直角三角形?
(1)a=7,b=24,c=25;
(2)a= 、b=1、c= .练一练:根据下列条件,判断下面以a,b,c为边的三角形是不是直角三角形?
(1)a=20,b=21,c=29
(2)a=5,b=7,c=8
(3)a= ,b= ,c=2
(4)a:b:c=2:3:41. 下列各数组中,不能作为直角三角形的三边长的
是( ).
A.3,4,5;
B.10,6,8;
C.4,5,6;
D.12,13,5.试一试C2.若△ABC的两边长为8和15,则能使△ ABC为直
角三角形的第三边的平方是( )
A.161; B.289;
C.17; D.161或289.D能够成为直角三角形三边长的三个
正整数,称为勾股数(或勾股弦数)。你能找出多少组勾股数?例2 如果△ABC的三边长分别为 a,b,c,且
a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)
则△ABC是直角三角形
解:∵ a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)∴a2+b2=(m2-n2)2+(2mn)2=m4-2m2n2+n4+4m2n2=m4+2m2n2+n4=(m2+n2)2=c2∴△ABC是直角三角形。
(1)、如图,图形A,B,C都是正方形,且A的面积+B的面积=C的面积,则图中的三角形是什么三角形?
练一练: (2) 、要做一个如图所示的零件,按规定∠B与∠D都应为直角,工人师傅量得所做零件的尺寸如图,这个零件符合要求吗 ? (3)、设△ABC的3条边长分别是a、b、c,且a=n2-1,b=2n,c=n2+1.问:△ABC是直角三角形吗?
应用拓展:如图:边长为4的正方形ABCD中,F是DC的中
点,且CE= BC,则AF⊥EF,试说明理由解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25∴AD=4,DF=2,FC=2,EC=1∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF 通过本节课的学习,你学到了什么?你知道一个三角形的三边在数量上满足怎样的关系时,这个三角形才是直角三角形呢?还有什么困惑?
本课总结:
(2)b=7,c=9,则a=_____.思考:若一个直角三角形的两条边长分别是3㎝和4㎝,求这个直角三角形的周长?古埃及人曾用下面的方法得到直角:
他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形。其直角在第4个结处。他们真的能够得到直角三角形吗?我们也来试一试合作学习(1)画三个三角形,使其边长分别为3㎝,4㎝,5㎝;5㎝,12㎝,13㎝;8㎝,15㎝,17㎝(2)算一算较短两条边长的平方和与最长一条边长的平方是否相等?(3)用量角器量一量,它们都是什么三角形?由此,你能得到怎样的猜想?如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。勾股定理的逆定理(1)上述结论中,哪条边所对的角是直角?
(2)如果三角形中较短两边的平方和不等于
最长的平方,那么这个三角形是直角三角形吗?想一想:例1.根据下列条件,分别判断以a,b,c
为边的三角形是不是直角三角形?
(1)a=7,b=24,c=25;
(2)a= 、b=1、c= .练一练:根据下列条件,判断下面以a,b,c为边的三角形是不是直角三角形?
(1)a=20,b=21,c=29
(2)a=5,b=7,c=8
(3)a= ,b= ,c=2
(4)a:b:c=2:3:41. 下列各数组中,不能作为直角三角形的三边长的
是( ).
A.3,4,5;
B.10,6,8;
C.4,5,6;
D.12,13,5.试一试C2.若△ABC的两边长为8和15,则能使△ ABC为直
角三角形的第三边的平方是( )
A.161; B.289;
C.17; D.161或289.D能够成为直角三角形三边长的三个
正整数,称为勾股数(或勾股弦数)。你能找出多少组勾股数?例2 如果△ABC的三边长分别为 a,b,c,且
a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)
则△ABC是直角三角形
解:∵ a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)∴a2+b2=(m2-n2)2+(2mn)2=m4-2m2n2+n4+4m2n2=m4+2m2n2+n4=(m2+n2)2=c2∴△ABC是直角三角形。
(1)、如图,图形A,B,C都是正方形,且A的面积+B的面积=C的面积,则图中的三角形是什么三角形?
练一练: (2) 、要做一个如图所示的零件,按规定∠B与∠D都应为直角,工人师傅量得所做零件的尺寸如图,这个零件符合要求吗 ? (3)、设△ABC的3条边长分别是a、b、c,且a=n2-1,b=2n,c=n2+1.问:△ABC是直角三角形吗?
应用拓展:如图:边长为4的正方形ABCD中,F是DC的中
点,且CE= BC,则AF⊥EF,试说明理由解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25∴AD=4,DF=2,FC=2,EC=1∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF 通过本节课的学习,你学到了什么?你知道一个三角形的三边在数量上满足怎样的关系时,这个三角形才是直角三角形呢?还有什么困惑?
本课总结:
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
