2024-2025学年上海奉贤区高二下学期数学期末区统考试卷(含答案)
文档属性
| 名称 | 2024-2025学年上海奉贤区高二下学期数学期末区统考试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 818.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 13:47:40 | ||
图片预览



文档简介
奉贤区2024~2025学年高二下学期期末考试
2025.6
一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)
1.抛物线的焦点坐标为___________.
2.在等差数列中,已知,则___________.
3.在平面直角坐标系中,,则___________.
4.已知,则曲线在点处的切线方程为___________.
5.已知直线与圆相交于两点,则___________.
6.某班要选举班干部,现有10名候选人,从这10名候选人中任选5人组成班委,有___________种不同的选法.(结果用数字表示)
7.在的二项展开式中系数最大的项的系数是___________.(结果用数字表示)
8.某公司生产的糖果每包标识质量是500g,但公司承认实际质量存在误差,已知每包糖果的实际质量服从的正态分布,随意买一包该公司生产的糖果,其质量误差超过5g(即)的可能性为___________.(结果精确到)
(参考数据:若,则,
9.若点在曲线上,点在曲线上,定义.已知有两条直线分别为,则___________.
10.设函数,其中,定义域为.对于,定义,则___________.
11.已知,对于任意的实数,都有恒成立,则的最小值是___________.
12.点是双曲线的左、右焦点,过点的直线与双曲线的左、右两支分别交于两点.若组成一个直角三角形,且其中两条直角边的长度分别为3和4,则满足条件的双曲线的离心率有___________种情况.
二、单项选择题(本题共4小题,13~14每小题4分,15~16每小题5分,共18分.)
13.已知变量与负相关,且由观测数据得到样本的平均数,则由观测数据得到的回归方程可能是( ).
A. B. C. D.
14.如图,在棱长为2的正四面体中,是的中心,则下列正确的是( ).
A. B.
C. D.
15.函数图像上存在点,使得不等式成立,则称函数为“向心函数”,下列四个选项中,是向心函数的为( ).
A. B. C. D.
16.圆锥的母线长为6cm,下面有两个判断,则正确的判断是( ).
①当圆锥的母线与底面所成角为时,圆锥的体积最大.
②圆锥的体积可以取到88.
A.①②都正确 B.①正确,②错误
C.①②都错误 D.①错误,②正确
三、解答题(本题共5小题,17~19题每题14分,20~21题每题18分,共78分.)
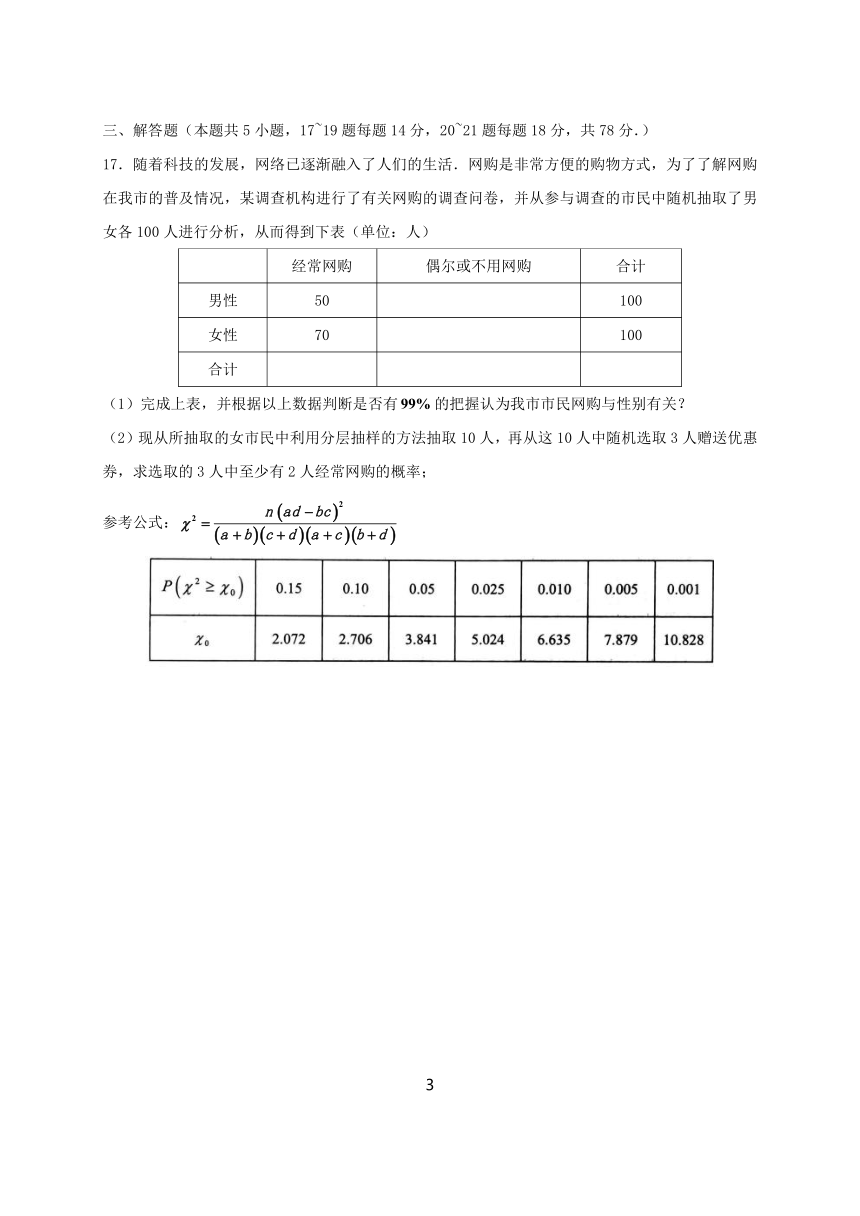
17.随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到下表(单位:人)
经常网购 偶尔或不用网购 合计
男性 50 100
女性 70 100
合计
(1)完成上表,并根据以上数据判断是否有的把握认为我市市民网购与性别有关?
(2)现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
参考公式:
18.如图,已知点为所在平面外一点,若平面.
(1)求证:面面;
(2)若与面所成的角的大小为,,求点到平面的距离.
19.已知无穷数列.若对任意的正整数,都有,则称与“伴随”.
(1)若,判断与是否“伴随”,说明理由;
(2)已知数列的前项和为满足,证明:与“伴随”.
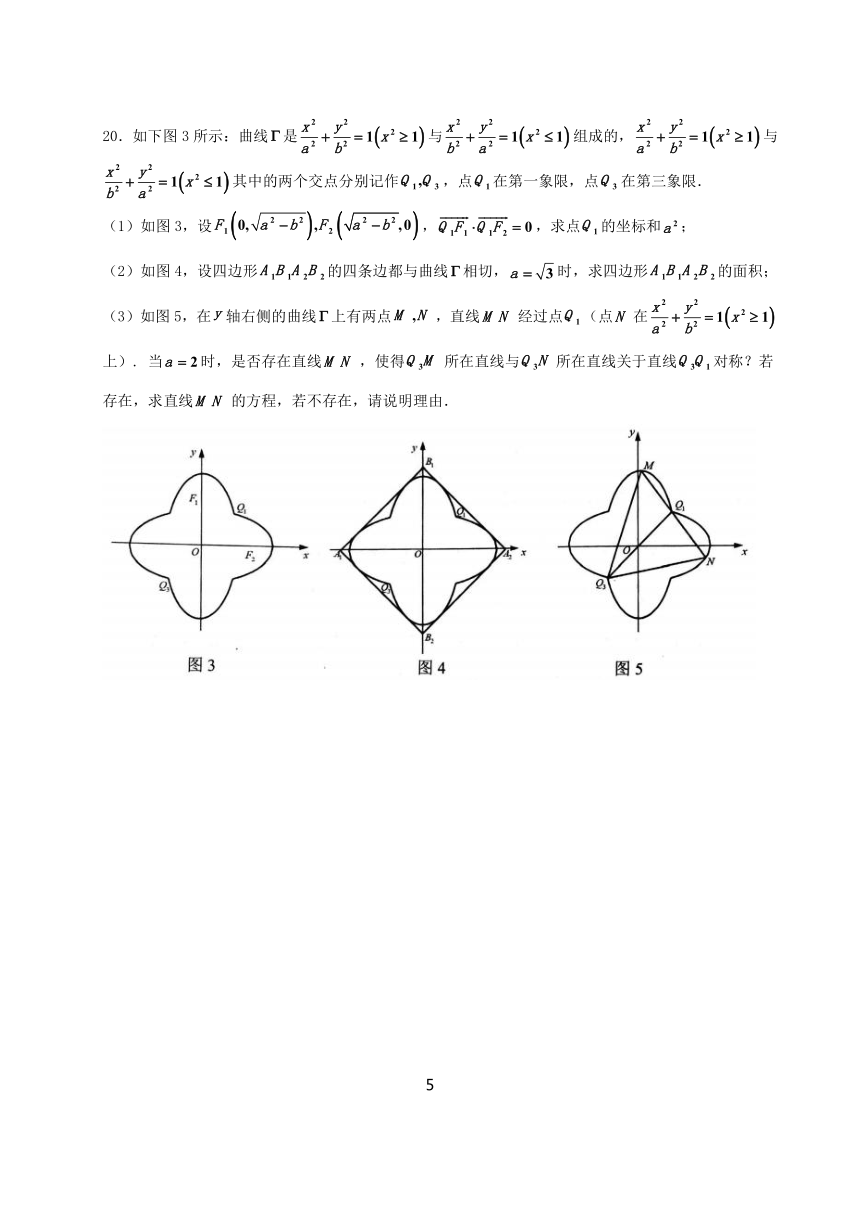
20.如下图3所示:曲线是与组成的,与其中的两个交点分别记作,点在第一象限,点在第三象限.
(1)如图3,设,,求点的坐标和;
(2)如图4,设四边形的四条边都与曲线相切,时,求四边形的面积;
(3)如图5,在轴右侧的曲线上有两点,直线经过点(点在上). 当时,是否存在直线,使得所在直线与所在直线关于直线对称?若存在,求直线的方程,若不存在,请说明理由.
21.已知函数,数列满足且.对任意正整数,恒成立时,则称函数具有性质T.
(1)任意取一个,判断函数是否具有性质T;
(2)函数在定义域上严格减,任意取一个,说明函数不具有性质T;
(3)求函数的单调区间,并判断当时,函数是否具有性质T,说明理由.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.;
7.; 8.; 9.; 10.; 11.; 12.5
11.已知,对于任意的实数,都有恒成立,则的最小值是___________.
【答案】
【解析】由得,化简得恒成立,所以,即,从而可得,∴.
设,以为轴建系,则,再设,
则
.
其几何意义为圆上的一动点到两定点的距离之和.
经计算可知:直线恰好与圆相切,故位于切点时,可使得线段之和最小,最小值为,如图所示.
12.点是双曲线的左、右焦点,过点的直线与双曲线的左、右两支分别交于两点.若组成一个直角三角形,且其中两条直角边的长度分别为3和4,则满足条件的双曲线的离心率有___________种情况.
【答案】5
【解析】依题意可得:共有如下6种情况,分别对应的离心率为:①;②;③;④5;
⑤;⑥.
① ②
③ ④
⑤ ⑥
二、选择题
13.B 14. D 15.B 16.B
16.圆锥的母线长为6cm,下面有两个判断,则正确的判断是( ).
①当圆锥的母线与底面所成角为时,圆锥的体积最大.
②圆锥的体积可以取到88.
A.①②都正确 B.①正确,②错误
C.①②都错误 D.①错误,②正确
【解析】设母线与底面所成角为,则半径,高为,
则.
设,并设,则可得,其中.
易得,令得(负舍).
则时,,单调递增;
时,,单调递减;
所以当时,即时,,
此时,所以①对,②错,选B.
三、解答题
17.(1)有关;(2).
18.(1)证明略;(2).
19.(1)不伴随,理由略;(2)证明略.
20.如下图3所示:曲线是与组成的,与其中的两个交点分别记作,点在第一象限,点在第三象限.
(1)如图3,设,,求点的坐标和;
(2)如图4,设四边形的四条边都与曲线相切,时,求四边形的面积;
(3)如图5,在轴右侧的曲线上有两点,直线经过点(点在上). 当时,是否存在直线,使得所在直线与所在直线关于直线对称?若存在,求直线的方程,若不存在,请说明理由.
【答案】(1),;(2)9;(3).
【解析】(1)根据对称性可知:,代入曲线方程得;
由可知,即;可求得;
(2),由得,此时曲线为和.
根据对称性,只需考虑第一象限内的情况即可.
设直线方程为,联立得. 由得.
所以直线为,所以四边形面积为.
(3)时,由得,此时曲线为和.
当所在直线与所在直线关于直线对称时,.
根据对称性可知,∴直线的方程为,即.
联立得,得,并不是轴右侧,故不存在符合要求的直线.
21.已知函数,数列满足且.对任意正整数,恒成立时,则称函数具有性质T.
(1)任意取一个,判断函数是否具有性质T;
(2)函数在定义域上严格减,任意取一个,说明函数不具有性质T;
(3)求函数的单调区间,并判断当时,函数是否具有性质T,说明理由.
【答案】(1)不具有性质T;(2);(3)不具有性质T.
【解析】(1)对于,,,此时,并不满足,故不具有性质T;
(3)由得.
所以的单调递增区间为,单调减区间为.
所以的最小值为.
再设. 则.
即在单调递减,且.
所以当时,,即,即时,;
当时,,即,即时,.
若时,可得,且,∴,
∴,,故,故当时,函数不具有性质T.
2025.6
一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)
1.抛物线的焦点坐标为___________.
2.在等差数列中,已知,则___________.
3.在平面直角坐标系中,,则___________.
4.已知,则曲线在点处的切线方程为___________.
5.已知直线与圆相交于两点,则___________.
6.某班要选举班干部,现有10名候选人,从这10名候选人中任选5人组成班委,有___________种不同的选法.(结果用数字表示)
7.在的二项展开式中系数最大的项的系数是___________.(结果用数字表示)
8.某公司生产的糖果每包标识质量是500g,但公司承认实际质量存在误差,已知每包糖果的实际质量服从的正态分布,随意买一包该公司生产的糖果,其质量误差超过5g(即)的可能性为___________.(结果精确到)
(参考数据:若,则,
9.若点在曲线上,点在曲线上,定义.已知有两条直线分别为,则___________.
10.设函数,其中,定义域为.对于,定义,则___________.
11.已知,对于任意的实数,都有恒成立,则的最小值是___________.
12.点是双曲线的左、右焦点,过点的直线与双曲线的左、右两支分别交于两点.若组成一个直角三角形,且其中两条直角边的长度分别为3和4,则满足条件的双曲线的离心率有___________种情况.
二、单项选择题(本题共4小题,13~14每小题4分,15~16每小题5分,共18分.)
13.已知变量与负相关,且由观测数据得到样本的平均数,则由观测数据得到的回归方程可能是( ).
A. B. C. D.
14.如图,在棱长为2的正四面体中,是的中心,则下列正确的是( ).
A. B.
C. D.
15.函数图像上存在点,使得不等式成立,则称函数为“向心函数”,下列四个选项中,是向心函数的为( ).
A. B. C. D.
16.圆锥的母线长为6cm,下面有两个判断,则正确的判断是( ).
①当圆锥的母线与底面所成角为时,圆锥的体积最大.
②圆锥的体积可以取到88.
A.①②都正确 B.①正确,②错误
C.①②都错误 D.①错误,②正确
三、解答题(本题共5小题,17~19题每题14分,20~21题每题18分,共78分.)
17.随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到下表(单位:人)
经常网购 偶尔或不用网购 合计
男性 50 100
女性 70 100
合计
(1)完成上表,并根据以上数据判断是否有的把握认为我市市民网购与性别有关?
(2)现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
参考公式:
18.如图,已知点为所在平面外一点,若平面.
(1)求证:面面;
(2)若与面所成的角的大小为,,求点到平面的距离.
19.已知无穷数列.若对任意的正整数,都有,则称与“伴随”.
(1)若,判断与是否“伴随”,说明理由;
(2)已知数列的前项和为满足,证明:与“伴随”.
20.如下图3所示:曲线是与组成的,与其中的两个交点分别记作,点在第一象限,点在第三象限.
(1)如图3,设,,求点的坐标和;
(2)如图4,设四边形的四条边都与曲线相切,时,求四边形的面积;
(3)如图5,在轴右侧的曲线上有两点,直线经过点(点在上). 当时,是否存在直线,使得所在直线与所在直线关于直线对称?若存在,求直线的方程,若不存在,请说明理由.
21.已知函数,数列满足且.对任意正整数,恒成立时,则称函数具有性质T.
(1)任意取一个,判断函数是否具有性质T;
(2)函数在定义域上严格减,任意取一个,说明函数不具有性质T;
(3)求函数的单调区间,并判断当时,函数是否具有性质T,说明理由.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.;
7.; 8.; 9.; 10.; 11.; 12.5
11.已知,对于任意的实数,都有恒成立,则的最小值是___________.
【答案】
【解析】由得,化简得恒成立,所以,即,从而可得,∴.
设,以为轴建系,则,再设,
则
.
其几何意义为圆上的一动点到两定点的距离之和.
经计算可知:直线恰好与圆相切,故位于切点时,可使得线段之和最小,最小值为,如图所示.
12.点是双曲线的左、右焦点,过点的直线与双曲线的左、右两支分别交于两点.若组成一个直角三角形,且其中两条直角边的长度分别为3和4,则满足条件的双曲线的离心率有___________种情况.
【答案】5
【解析】依题意可得:共有如下6种情况,分别对应的离心率为:①;②;③;④5;
⑤;⑥.
① ②
③ ④
⑤ ⑥
二、选择题
13.B 14. D 15.B 16.B
16.圆锥的母线长为6cm,下面有两个判断,则正确的判断是( ).
①当圆锥的母线与底面所成角为时,圆锥的体积最大.
②圆锥的体积可以取到88.
A.①②都正确 B.①正确,②错误
C.①②都错误 D.①错误,②正确
【解析】设母线与底面所成角为,则半径,高为,
则.
设,并设,则可得,其中.
易得,令得(负舍).
则时,,单调递增;
时,,单调递减;
所以当时,即时,,
此时,所以①对,②错,选B.
三、解答题
17.(1)有关;(2).
18.(1)证明略;(2).
19.(1)不伴随,理由略;(2)证明略.
20.如下图3所示:曲线是与组成的,与其中的两个交点分别记作,点在第一象限,点在第三象限.
(1)如图3,设,,求点的坐标和;
(2)如图4,设四边形的四条边都与曲线相切,时,求四边形的面积;
(3)如图5,在轴右侧的曲线上有两点,直线经过点(点在上). 当时,是否存在直线,使得所在直线与所在直线关于直线对称?若存在,求直线的方程,若不存在,请说明理由.
【答案】(1),;(2)9;(3).
【解析】(1)根据对称性可知:,代入曲线方程得;
由可知,即;可求得;
(2),由得,此时曲线为和.
根据对称性,只需考虑第一象限内的情况即可.
设直线方程为,联立得. 由得.
所以直线为,所以四边形面积为.
(3)时,由得,此时曲线为和.
当所在直线与所在直线关于直线对称时,.
根据对称性可知,∴直线的方程为,即.
联立得,得,并不是轴右侧,故不存在符合要求的直线.
21.已知函数,数列满足且.对任意正整数,恒成立时,则称函数具有性质T.
(1)任意取一个,判断函数是否具有性质T;
(2)函数在定义域上严格减,任意取一个,说明函数不具有性质T;
(3)求函数的单调区间,并判断当时,函数是否具有性质T,说明理由.
【答案】(1)不具有性质T;(2);(3)不具有性质T.
【解析】(1)对于,,,此时,并不满足,故不具有性质T;
(3)由得.
所以的单调递增区间为,单调减区间为.
所以的最小值为.
再设. 则.
即在单调递减,且.
所以当时,,即,即时,;
当时,,即,即时,.
若时,可得,且,∴,
∴,,故,故当时,函数不具有性质T.
同课章节目录
