2026年高考数学复习资料 真题分类汇编—等差数列(含解析)
文档属性
| 名称 | 2026年高考数学复习资料 真题分类汇编—等差数列(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 13:46:53 | ||
图片预览




文档简介
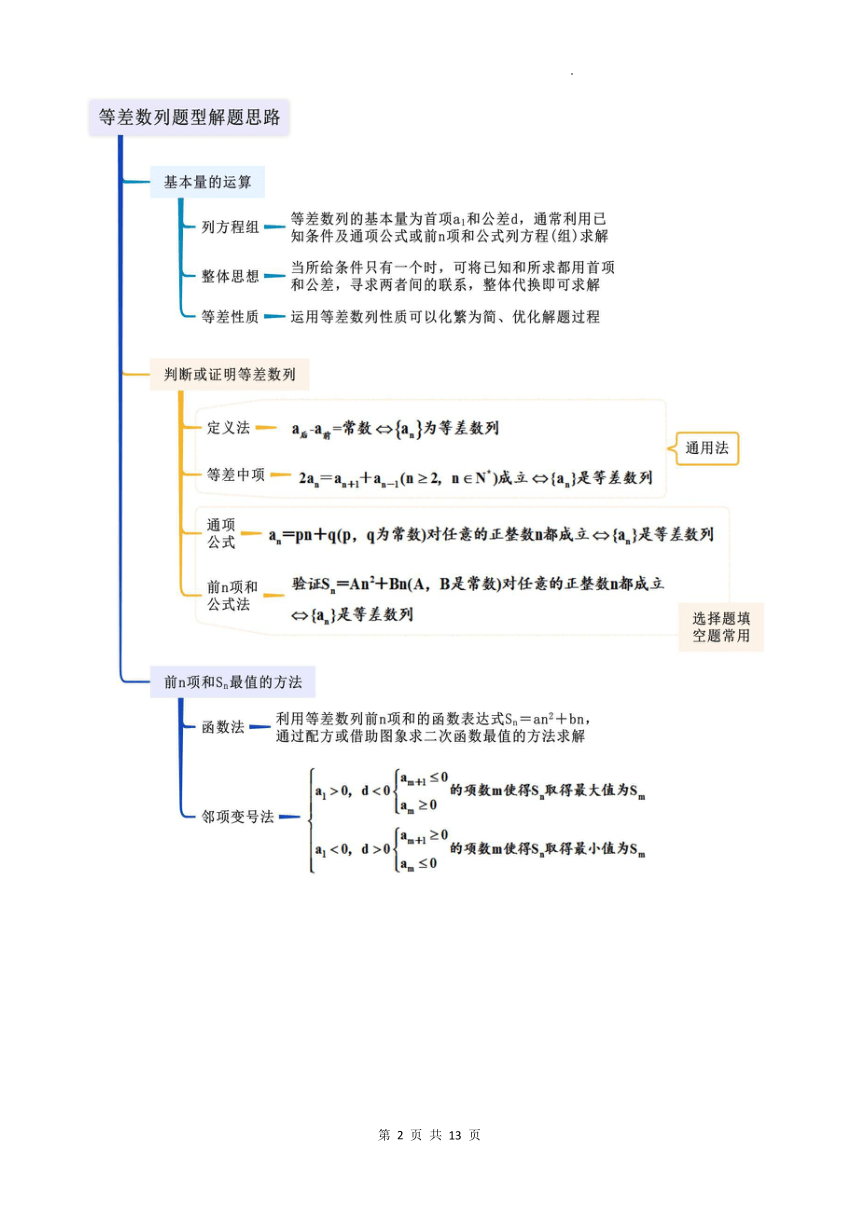
等差数列(精讲精练)
考向一 等差数列基本量的计算
【例 1-1】(2025·山东德州·三模)已知Sn 为等差数列 an 的前n 项和, a2 4, S5 3a4 6 ,则a8 ( )
B.8 C.16 D.32
【例 1-2】(2025·广西柳州·模拟预测)设等差数列 an 的前n 项和为 Sn ,若 S4 S1 9, a1 a4 5 ,则 an 的公差为( )
A.1 B.2 C.3 D.4
【例 1-3】(2025·湖北黄冈·模拟预测)设等差数列 an 的前n 项和为 Sn ,若Sm 3, Sm 1 0, Sm 2 4 ,则m ( )
A.8 B.7 C.6 D.5
【一隅三反】【公众号:林樾数学】
1.(2025·北京·高考真题)已知 an 是公差不为零的等差数列, a1 2 ,若a3 , a4 , a6 成等比数列,则a10 ( )
20
18
C.16 D.18
2.(2025·福建·模拟预测)已知 Sn 为等差数列 an 的前n 项和,若 a3 S3 2 , a4 S4 6 ,则 S9 ( )
A.28 B.32 C.36 D.40
3.(2025·黑龙江大庆·模拟预测)已知等差数列 an 的前n 项和为 Sn ,若S5 2S3 , a1 a8 10 ,则公差d 为( )
1 1 2
A. 4 B. 2 C. 3 D.1
4.(2025·浙江·三模)设等差数列 an 的前 n 项和为 Sn ,已知a2 3 , S5 25 ,则a3 2a6 ( )
5.(2025·山西·二模)已知等差数列{an }公差不为 0,记其前 n 项和为 Sn ,若a6 a5 a7 , S2k a2k ,则正整数 k
的值为( )
B.6 C.8 D.12
考向二 等差中项及应用
【例 2-1】(2026 高三·全国·专题练习)若a 是 1 和 3 的等差中项, b 是 1 和 4 的等比中项,则 a 的值为( )
b
1
2
1
2
C.1 D. 1
【例 2-2】(2025·宁夏银川·二模)已知等差数列 an 的前 n 项和为 Sn ,且a2 a4 6 ,则 S5 ( )
A.0 B.10 C.15 D.30
【例 2-3】(2025·广西·三模)在公差不为 0 的等差数列 a 中,若a 是a 与a 的等差中项,则 1 4 的最小值
为( )
3 5
n 3 x y x y
6 9
A. 2 B. 3 C. 5 D. 5
【例 2-4】(2025·山东·一模)已知(1 2x)n n N* 的展开式中第 2 项,第 3 项,第 4 项的二项式系数成等差数列,则n ( )
A.5 B.6 C.7 D.8
【一隅三反】
1.(2025·辽宁·一模)已知等差数列 an 的前n 项和为Sn ,若a3 a10 a6 4 ,则 S13 ( )
B.60 C.68 D.52
2.(23-24 浙江)在V ABC 中,三个内角 A, B,C 成等差数列,则sin A C ( )
1
A. 2
B. 2
2
C. 3
2
D.1
3.(2025·广东汕头·模拟预测)已知a, b R , b 为a 和2 的等差中项,则3a 1 的最小值为( )
9b
1 1 2
A. 3 B. 2 C. 2 D. 3
4(2025·安徽淮北·二模)若实数m 和n 的等差中项为 1,则m2 n2 的最小值为 .
考向三 等差数列前 n 项和最值
【例 3-1】(2025·广西南宁·三模)设等差数列 an 的前 n 项和为 Sn ,若a5 2 , a3 a8 12 a7 ,则 Sn 的最小值
为( )【公众号:林樾数学】
A. 14
B. 49
4
C. 12
D. 10
时n 的值为( )
A.12 B.13 C.14 D.25
【例 3-3】(24-25 高三下·云南昭通·阶段练习)已知数列{an }是等差数列,其前 n 项和为 Sn ,若a3 a10 0 ,S11 0 ,则数列{Sn } 中最小的项是( )
S4
S5
S6
S7
【一隅三反】
1.(2025·江西·模拟预测)记 Sn 为等差数列 an 的前 n 项和,且a2 2a1 2 ,则满足 Sn 888的 n 的最大值为
( )
A.40 B.41 C.42 D.43
2.(24-25 陕西西安·期末)设等差数列 an 的前n 项和为Sn ,若a5 a8 0 , S11 0 ,则 Sn 的最大值为( )
A. S5
B. S6
C. S7
D. S8
3.(2025·山东泰安·模拟预测)公差不为0 的等差数列 an 的前n 项和为 Sn ,若a7 2 , a9 , a5 , a13 成等比数列,则满足Sn 0 的n 的最大值为( )
A. 8 B. 9 C.13 D.14
4.(2025·甘肃金昌·模拟预测)(多选)许多已知等差数列 an 的公差d 0 ,其前 n 项和记为 Sn , a1 0 ,则下列说法正确的是( )
A.数列 an 中有最大项 B.数列 Sn 中有最小项
C.若a a 0 ,则 55 S10 45
D.若 S
a , S
a ,则 S 取最小值时n 9
10 11 d
20 20
21 21 n
考向四 等差数列片段和的性质
【例 4-1】(24-25 广西)已知等差数列 an 的前n 项和为 Sn ,且 S4 2, S8 6 ,则 S12 ( )
A.8 B.10 C.12 D.16
【例 4-2】(24-25 河南)已知等比数列 an 的前 n 项和为 Sn ,若 S6 7, S12 21 ,则 S24 ( )
A.56 B.105 C.112 D.189
【例 4-3】(23-24 甘肃 )设等差数列 a 的前n 项和为 S ,若 S14 7 ,则 S21 ( )
18 3
n n
7
11
S14
11
A. 7 B. 2 C. 7 D. 6
【例 4-4】(2024 高三·全国·专题练习)设等差数列 an 的前n 项和为Sn ,若 S12 288, S9 162 ,则S6 ( )
A.18 B.36 C.54 D.72
【一隅三反】
1.(24-25 江西)已知等差数列 an 的前n 项和为 Sn ,若 S3 12 , S6 S3 24 ,则 S12 S9 ( )
A.36 B.48 C.60 D.120
2.(24-25 四川)已知Sn 是等差数列 an 的前 n 项和,若 S20 15 , S40 40 ,则 S60 ( )
A.75 B.65 C.50 D.55
3.(2024·河南周口·模拟预测)设 Sn 为等差数列 an 的前 n 项和,已知 S3 4, S6 10 ,则a16 a17 a18 ( )
A.12 B.14 C.16 D.18
4.(2025·吉林长春·二模)已知等差数列 an 的前 n 项和为 Sn ,若 S3 S9 6 ,则 S12 的值为( )
A.0 B.3 C.6 D.12
5.(2025·四川)设等差数列 an 的前n 项和 Sn ,若 S3 9 , S6 36 ,则a7 a8 a9 ( )
A.18 B.27 C.45 D.63
6.(24-25 河南·阶段练习)已知等差数列{a }的前n 项和为S ,若 S3 3 ,则 S12 ( )
n n
6 9
3 3 5
A. 7 B.3 C. 2 D. 3
考向五 等差数列和与 n 的比值
【例 5-1】(2025·江西)已知数列 a 和 b 都是等差数列,且其前 n 项和分别为S 和T ,若 Sn 3n 1 ,则 a5
n n
( )
16 28 10
n n 2n 5 b
34
A. 15 B. 23 C. 11 D. 27
【例 5-2】(24-25 四川)已知等差数列 a , b 的前n 项和分别为 S ,T ,若 Sn 2n ,则 a2 a8 ( )
n n n n
T 3n 1
b b
20 5
n 3 7
10 9
A. 31 B. 8 C. 13 D. 14
【例 5-3】(2025·黑龙江哈尔滨·模拟预测)已知Sn , Tn 分别是等差数列 an , bn 的前 n 项和,且
Sn 2n 1 n N* ,则 a3 a8 ( )
Tn 4n 2
7
b4 b7
11
b5 b6
21 17
A. 10 B. 18 C. 38 D. 30
【例 5-4】(2025·湖北·模拟预测)已知等差数列 a , b 的前 n 项和分别为 S ,T ,若 Sn n ,则 a5 ( )
n n
5 9 9
n n 2n 1 b
3
A. 9 B. 17 C. 20 D. 5
【例 5-5】(23-24 湖北武汉)在等差数列 a 中, a 1,其前 n 项和为 S ,若 S8 S6 2 ,则 S 等于( )
n 1 n 8 6 10
A.10 B.100 C.110 D.120
【例 5-6】(23-24 高三上·河南·阶段练习)已知等差数列 a 的前 n 项和为 S ,且 S7 S3 4 ,则a a ( )
n n 7 3 9 6
A. 2 B. 3 C. 4 D. 6
【一隅三反】
1.(24-25 高三上·河南·期末)已知 S 与T 分别是等差数列 a 与等差数列 b 的前 n 项和,且 Sn 6n ,
则 a1
b6 b2020
a2025 b4 b2022
n n
( )
Tn n 2025
A.1 B.2 C.3 D.4
2.(2024·河北衡水·三模)已知数列 an , bn 均为等差数列,其前n 项和分别为Sn,Tn ,满足(2n 3)Sn (3n 1)Tn,则 a7 a8 a9 ( )
b6 b10
A.2 B.3 C.5 D.6
3.(2025 湖北)已知 S ,T 分别是等差数列 a , b 的前项和,且 Sn 2n 1 (n N* ) ,则 a10 a11 ( )
n n n n
T 4n 2
b b b b
21 23
n
43 41
3 18 6 15
A. 38 B. 42 C. 82 D. 78
4.(24-25 高三上·宁夏银川·阶段练习)已知等差数列 a 和 b 的前 n 项和分别为 S ,T ,若 Sn 3n 4 ,则
a3 a8 ( )
b2 b9
n n n n
Tn n 2
17 37 37 17
A. 13 B. 13 C. 6 D. 6
5.(2025·江苏)已知两个等差数列 a 和 b 的前 n 项和分别为 Sn 和 Tn,且 Sn = 2n 70 ,则 a7 的值为( )
n n
48 42 84
Tn n 3 b6
1
A. 7 B. 5 C. 9 D. 4
6.(23-24 河北保定·期末)已知数列 a 满足a a 6 , a 的前n 项和为S ,则 S2024 S2022 ( )
n n 1 n n
n 2024 2022
A.12 B. 6 C. 3 D. 2
7.(2025·贵州)等差数列 a 的前n 项和为S ,若 S2021 S2020 1 且a 3 ,则( )
n n 2021 2020 1
A. an 2n 1 B. an n 1
C. S 2n2 n D. S 4n2 n
8.(2024 高三·全国·专题练习)已知 Sn 是等差数列{an}的前 n 项和,若 a1=﹣2018, S2019 S2013
2019 2013
6 ,则 S2020
等于( )
A.﹣4040 B.﹣2020 C.2020 D.4040
考向六 等差数列的奇数项(偶数项)之和
【例 6-1】(2025 河南)一个等差数列共 100 项,其和为 80,奇数项和为 30,则该数列的公差为( )
1 1 2
A. 4 B.2 C. 3 D. 5
【例 6-2】(2025 陕西)等差数列 an 共 2n+1 个项,且奇数项和为 165,偶数项和为 150,则 n=( )
A.10 B.13 C.11 D.22
【一隅三反】
1.(2023·重庆·二模)已知等差数列 an 的前 30 项中奇数项的和为A ,偶数项的和为 B ,且 B A 45 ,
2 A B 615 ,则an ( )
3n 2
3n 1
3n 1
3n 2
2.(2025 河南)已知等差数列 a 的公差d 1 , a a a 80 ,那么 S ( )
n 2 2 4 100
100
A.80 B.120 C.135 D.160
3.(2025 上海)设等差数列的项数n 为奇数,则其奇数项之和与偶数项之和的比为( )
n 1
n
2n 1
n
2n 1
2n
n 1
n 1
考向七 等差数列的证明与判断
【例 6-1】(2025·全国一卷·高考真题)设数列 a 满足a 3 , an 1 an 1 ,证明: na 为等差数列;
n 1 n n 1 n(n 1) n
【例 6-2】(2025·福建厦门·三模)已知数列 a 的前项和为 S ,a 1,且na S n2 n ,证明:数列 Sn
为等差数列;
n n 1
n 1 n
【一隅三反】
1.(2025·江西新余·模拟预测)已知数列 a 的前n 项和为S , a 3S S 0 , a 1 .
1
n n n 1
n n 1 1 3
证明:数列
为等差数列;
n
求 an 的通项;
1
求 a 的最大值.
n
2.(24-25 高三下·甘肃庆阳·期中)记 Sn 为正项数列 an 的前n 项和,且a1Sn n 1 an .
求a1 的值;
判断 an 是否为等差数列,并求 a 的通项公式;
n
4.(2025·甘肃白银·模拟预测)已知数列 a 满足a 2 , a an , n为奇数,数列 b 满足b a .
n 1 n 1
a 1, n为偶数
n n 2n 1
n
证明:数列 bn 为等差数列;
求数列 bn 的通项公式及前 n 项和 Sn ;
考向八 含绝对值的等差数列的前 n 项和
【例 7-1】(23-24 高三上·贵州·阶段练习)记等差数列 an 的前n 项和为Sn ,已知a1 11, S3 S9 .
求 an 的通项公式;
记数列 an 的前n 项和为Tn ,求T100 .
【例 7-2】(24-25 高三上·湖北·开学考试)已知数列 an 的前n 项和为 Sn ,且a1 2, an 1 Sn 2 .
求数列 an 的通项公式;
设b
log a2 11,求数列 b 的前n 项和T .【公众号:林樾数学】
【一隅三反】
1.(2024·全国·模拟预测)已知等差数列 an , a1 10 ,记 Sn 为 an 的前n 项和,从下面①②③中再选取一
个作为条件,解决下面问题.① 2a a 0;② S 55 ;③ S7 S5 2 .
5 8 11 7 5
求Sn 的最小值;
设 an 的前n 项和为Tn ,求T20 .
2(2023·全国乙卷·高考真题)记 Sn 为等差数列 an 的前n 项和,已知a2 11, S10 40 .
求 an 的通项公式;
求数列 an 的前n 项和Tn .
考向九 等差数列的简单应用
【例 8-1】(23-24 高三下·重庆渝中·阶段练习)中国载人航天工程发射的第十八艘飞船,简称“神十八”,于 2024年 4 月执行载人航天飞行任务.运送“神十八”的长征二号F运载火箭,在点火第一秒钟通过的路程为2km ,以后每秒钟通过的路程都增加3km ,在达到离地面222km的高度时,火箭开始进入转弯程序.则从点火到进入转弯程序大约需要的时间是( )秒.【公众号:林樾数学】
A.10 B.11 C.12 D.13
【例 8-2】(24-25 山东 )“中国剩余定理”又称“孙子定理”,原文如下:今有物不知其数,三三数之剩二(除以 3余 2),五五数之剩三(除以 5 余 3),七七数之剩二(除以 7 余 2),问物几何?现有这样一个相关的问题:已知正整数 p( p 1) 满足二二数之剩一,三三数之剩一,将符合条件的所有正整数 p 按照从小到大的顺序排成一列,构
成数列 a ,记数列 a 的前 n 项和为 S ,则 2Sn an 23 的最小值为( )
n n n n
A.26 B.36 C.38 D.46
【一隅三反】
1.(2024·广东广州·模拟预测)元代数学家朱世杰编著的《算法启蒙》中记载了有关数列的计算问题:“今有竹七节,下两节容米四升,上两节容米二升,各节欲均容,问逐节各容几升?”其大意为:现有一根七节的竹子,最下面两节可装米四升,最上面两节可装米二升,如果竹子装米量逐节等量减少,问竹子各节各装米多少升?以此计算,这根竹子的装米量为( )
A. 9 升 B.10.5 升 C.12 升 D.13.5 升
2.(2025 江西抚州·期中)我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度),二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是( )
A.相邻两个节气晷长减少或增加的量为十寸 B.秋分的晷长为 75 寸
C.立秋的晷长比立春的晷长长
D.立冬的晷长为一丈五寸【公众号:林樾数学】
3.(2023·四川达州·一模)《孙子算经》是我国南北朝时著名的数学著作,其中有物不知数问题:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?意思是:有一些物品,不知道有多少个,只知道将它们三个三个地数,会剩下 2 个;五个五个地数,会剩下 3 个;七个七个地数,也会剩下 2 个.这些物品
的数量是多少个?若一个正整数除以三余二,除以五余三,将这样的正整数由小到大排列,则前 5 个数的和为
( )
A.189 B.190 C.191 D.192
等差数列(精讲精练)解析版
考向一 等差数列基本量的计算
【例 1-1】(2025·山东德州·三模)已知Sn 为等差数列 an 的前n 项和, a2 4, S5 3a4 6 ,则a8 ( )
B.8 C.16 D.32
【答案】C
【解析】设等差数列 a 的公差为d ,由题意得 a1 d 4
,解得 a1 2 ,所以a a 7d 16 .
5a1 10d 3a1 9d 6
d 2 8 1
故选:C
【例 1-2】(2025·广西柳州·模拟预测)设等差数列 an 的前n 项和为 Sn ,若 S4 S1 9, a1 a4 5 ,则 an 的公差为( )
A.1 B.2 C.3 D.4
【答案】A
【解析】因为 S4 S1 9, a1 a4 5 ,所以a2 a3 a4 3a3 9 ,解得a3 3,又a1 a4 a2 a3 5 ,所以a2 2 ,所以公差为a3 a2 1.故选:A.
【例 1-3】(2025·湖北黄冈·模拟预测)设等差数列 an 的前n 项和为 Sn ,若Sm 3, Sm 1 0, Sm 2 4 ,则m ( )
A.8 B.7 C.6 D.5
【答案】C
【解析】方法一:由题意得: am 1 Sm 1 Sm 3 , am 2 Sm 2 Sm 1 4 ,
则等差数列的公差d am 2
am 1
1,则a1
3 m , Sm
m 3 m m m 1 3,所以m 6 .
2
方法二:因为等差数列的性质即 Sn 为等差数列,则 Sm Sm 2 2Sm 1 ,得 3 4 0 ,解得m 6 .
故选:C
【一隅三反】
m m 2
m 1
m m 2
1.(2025·北京·高考真题)已知 an 是公差不为零的等差数列, a1 2 ,若a3 , a4 , a6 成等比数列,则a10 ( )
20
18
C.16 D.18
【答案】C
【解析】设等差数列 an 的公差为d , d 0 ,
因为a , a , a 成等比数列,且a 2 ,所以a2 a a
,即 2 3d 2 2 2d 2 5d ,解得d 2 或d 0 (舍
去),所以a10 a1 9d 2 9 2 16.故选:C.
2.(2025·福建·模拟预测)已知 Sn 为等差数列 an 的前n 项和,若 a3 S3 2 , a4 S4 6 ,则 S9 ( )
A.28 B.32 C.36 D.40
【答案】C
【解析】设等差数列 an 的公差为d ,因为a3 S3 2 , a4 S4 6 ,故两式作差可得:
a a S S 4 ,即d a 4 , a 4 ,又 S 9 a1 a9 9a ,故 S 36 .
4 3 4 3
故选:C.
4 5 9 2 5 9
3.(2025·黑龙江大庆·模拟预测)已知等差数列 an 的前n 项和为 Sn ,若S5 2S3 , a1 a8 10 ,则公差d 为( )
1 1 2
A. 4 B. 2 C. 3 D.1
【答案】C
【解析】由S 2S ,则 5(a1 a5 ) 2 3(a1 a3 ) ,即5a 6a ,所以5(a d ) 6a 5d a ,则a 4d ,
5 3 2 2
3 2 2 2 2 1
由a a 2a 7d 15d 10 ,则 d 2 .故选:C
1 8 1 3
4.(2025·浙江·三模)设等差数列 an 的前 n 项和为 Sn ,已知a2 3 , S5 25 ,则a3 2a6 ( )
A.17 B.21 C.23 D.27
【答案】D
【解析】设等差数列 a 的公差为d ,由题意得 a1 d 3 ,解得 a1 1,所以a 2a 3a 12d 27 .故
5a1 10d 25
d 2
3 6 1
选:D.
5.(2025·山西·二模)已知等差数列{an }公差不为 0,记其前 n 项和为 Sn ,若a6 a5 a7 , S2k a2k ,则正整数 k
的值为( )
B.6 C.8 D.12
【答案】B
【解析】设等差数列{an }公差为d , d 0 ,由a6 a5 a7 ,得a6 2a6 ,解得a6 0 ,
a a 5d 5d , a a (n 1)d (n 6)d , S 5d (2k 6)d 2k ,
1 6 n 1
2k 2
因此 5d (2k 6)d 2k (2k 6)d ,整理得2k 2 13k 6 0 ,解得k 6 .故选:B
2
考向二 等差中项及应用
【例 2-1】(2026 高三·全国·专题练习)若a 是 1 和 3 的等差中项, b 是 1 和 4 的等比中项,则 a 的值为( )
b
1
2
【答案】D
1
2
C.1 D. 1
【解析】由题知2a 1 3 ,所以a 2 ,由b2 4 得b 2 ,所以 a 1 .故选:D.
b
【例 2-2】(2025·宁夏银川·二模)已知等差数列 an 的前 n 项和为 Sn ,且a2 a4 6 ,则 S5 ( )
A.0 B.10 C.15 D.30
【答案】C
【解析】因为a a 6, 所以2a 6, a
3. 又因为 S
5 a1 a5 5a
15, 故选:C.
2 4 3 3
5 2 3
【例 2-3】(2025·广西·三模)在公差不为 0 的等差数列 a 中,若a 是a 与a 的等差中项,则 1 4 的最小值
为( )
3 5
n 3 x y x y
6 9
A. 2 B. 3 C. 5 D. 5
【答案】A
【解析】因为在公差不为 0 的等差数列 an 中, a3 是ax 与ay 的等差中项,所以2a3 ax ay ,所以 x y 6 ,
1 4 1 x y
1 4 1 5 y 4 x 1
2 3
y 4x
y 4
所以
x y 6
x y 6
x y
6 5
2
,当且仅当 x y
,即 x 2 ,
时等号
成立,所以 1 4 的最小值为 3 .故选: A .
x y 2
【例 2-4】(2025·山东·一模)已知(1 2x)n n N* 的展开式中第 2 项,第 3 项,第 4 项的二项式系数成等差数列,则n ( )
A.5 B.6 C.7 D.8
【答案】C
【解析】已知(1 2x)n n N* 的展开式中第 2 项,第 3 项,第 4 项的二项式系数为C1 , C2 , C3 ,
依题意成等差数列,故2C2 C1 C3 ,得到: 2 n n 1 n n n 1 n 2 ,
n n n
2 1 3 2 1
化简得6 n 1 6 n 1 n 2 ,即: n2 9n 14 0 ,解得: n 7 或n 2 (舍去)故选:C
【一隅三反】
1.(2025·辽宁·一模)已知等差数列 an 的前n 项和为Sn ,若a3 a10 a6 4 ,则 S13 ( )
B.60 C.68 D.52
【答案】D
【解析】a a a a a 4 ,∴ a 4 ,∴ S
13 a1 a13 13a
52 ,故选:D.
3 10 6 7 6 7
13 2 7
2.(23-24 浙江)在V ABC 中,三个内角 A, B,C 成等差数列,则sin A C ( )
1
A. 2
【答案】C
B. 2
2
C. 3
2
D.1
【解析】因为 A, B,C 成等差数列,所以 A+C = 2B ;
又 A B C π ,所以3B π ,即 B π ,所以 A C 2B 2π ,所以sin A C sin 2 π 3 .故选:C.
3 3 3 2
3.(2025·广东汕头·模拟预测)已知a, b R , b 为a 和2 的等差中项,则3a 1 的最小值为( )
9b
1 1 2
A. 3 B. 2 C. 2 D. 3
【答案】D
【解析】由题知2b a 2 ,得到a 2b 2 ,所以3a 1
9b
32b 2 1
9b
9b 1 1
9b
1 9b 1 2
9 9b
2 ,
3
当且仅当 1 9b 1
9 9b
,即b 1 , a 1时,取等号.故选:D.
2
4(2025·安徽淮北·二模)若实数m 和n 的等差中项为 1,则m2 n2 的最小值为 .
【答案】2
【解析】若实数m 和n 的等差中项为 1,则m n 2 , m2 n2 2mn ,即2 m2 n2 m n 2 ,
m n 2 22
即m2 n2 2 ,当且仅当m n 1取等号.故
2 2
m2 n2 的最小值为 2.故答案为:2.
考向三 等差数列前 n 项和最值
【例 3-1】(2025·广西南宁·三模)设等差数列 an 的前 n 项和为 Sn ,若a5 2 , a3 a8 12 a7 ,则 Sn 的最小值为( )
14
【答案】C
49
4
12
10
【解析】假设等差数列 an 的公差为d ,由a3 a8 12 a7 得a3 a7 12 a8, 2a5 12 a5 3d 12 a5 3d,
所以3d 12 3a5 12 6 6 ,所以d 2 ,故an a5 (n 5)d 2n 8 ,
n a a n 6 2n 8
7 2 49
则S 1 n n n 7
n
则 Sn
S3 S4 12 .故选:C.
n 2 2
2 4
min
【例 3-2】(2025·江苏盐城·模拟预测)设等差数列 an 的前n 项和为 Sn ,若a1 0 , S9 S19 ,则当 Sn 取最小值时n 的值为( )
A.12 B.13 C.14 D.25
【答案】C
【解析】由S9 S19 可得a10 a11 a19 0 ,由等差数列的性质可得: 5(a14 a15 ) 0 ,因a1 0 ,则等差数列 an 的公差d 0 ,即等差数列 an 为递增数列,
故a14 0, a15 0 ,即 Sn 取最小值时, n 的值为 14.故选:C.
【例 3-3】(24-25 高三下·云南昭通·阶段练习)已知数列{an }是等差数列,其前 n 项和为 Sn ,若a3 a10 0 ,S11 0 ,则数列{Sn } 中最小的项是( )
S4
S5
S6
S7
【答案】C
【解析】因为 S
11(a1 a11 ) 11a
0 ,所以a 0 ,因为a a
a a
0 ,所以a 0 ,
11 2 6
6 6 7 3 10 7
所以公差d a7 a6 0 ,故当n 6 时, an 0 ,当n 7 时, an 0 ,所以当n 6 时, Sn 取得最小值,即{Sn } 中
最小的项是S6 ,故选:C.
【一隅三反】
1.(2025·江西·模拟预测)记 Sn 为等差数列 an 的前 n 项和,且a2 2a1 2 ,则满足 Sn 888的 n 的最大值为
( )
A.40 B.41 C.42 D.43
【答案】B
【解析】由已知可得a 1, a 2 , a 的公差为a a 1,故 a n ,故 S 1 2 3 n n(n 1) ,
2 n
1 n n 2
令 n(n 1) 888 ,又n N* ,所以n 41 ,故 n 的最大值为 41,
2
验证 S41
41 42 861 888 , S
2 42
42 43 903 888 ,所以 n 的最大值为 41.故选:B.
2
2.(24-25 陕西西安·期末)设等差数列 an 的前n 项和为Sn ,若a5 a8 0 , S11 0 ,则 Sn 的最大值为( )
A. S5
B. S6
C. S7
D. S8
【答案】B
【解析】因为数列 an 为等差数列,由a5 a8 0 a6 a7 0 ;
由S 0 11 a1 a11 0 a a 0 a 0 .所以a 0 .
11 1 11 6 7
所以等差数列 an 是首项为正数的递减数列,且前 6 项为正,从第 7 项开始为负数.所以 S6 最大.故选:B 3.(2025·山东泰安·模拟预测)公差不为0 的等差数列 an 的前n 项和为 Sn ,若a7 2 , a9 , a5 , a13 成等比数列,则满足Sn 0 的n 的最大值为( )
A. 8 B. 9 C.13 D.14
【答案】D
【解析】设数列 an 的公差为d ,
a1 6d 2
因为a 2 , a , a , a 成等比数列,所以
a1 20
, 解得 ,
7 9 5 13
a 8d a 12d a 4d 2
d 3
1 1 1
所以an
23 3n ,故 Sn
n 20 (23 3n) n(43 3n)
.
2 2
由S 0 ,得 n(43 3n) 0 ,解得0 n 43 . ∵ n N ,∴ n 的最大值为14 .故选:D.
n 2 3
4.(2025·甘肃金昌·模拟预测)()许多已知等差数列 an 的公差d 0 ,其前 n 项和记为 Sn , a1 0 ,则下列说法正确的是( )
A.数列 an 中有最大项 B.数列 Sn 中有最小项
C.若a a 0 ,则 55 S10 45
D.若 S
a , S
a ,则 S 取最小值时n 9
10 11 d
【答案】BC
20 20
21 21 n
【解析】对于 A,因为an a1 n 1 d ,且d 0 ,故 an 中无最大项,A 错误;
对于 B, a1 0 , d 0 ,故 m N* ,a 0 ,a 0 ,则Sm 为 Sn 中的最小项(当am 1 0 时, Sm , Sm 1 均
m 1
为 Sn 中的最小项),B 正确;
对于 C,若a a 0 ,则可知a 0, a 0 ,即a 9d 0 a 10d ,则可知 10 a1 9 ,故
10 11
10 11 1 1 d
S10 10a1 45d 10 a1 45 55, 45 ,C 正确;
d d d
对于 D,S20 a20 ,则可知 S19 0 ,则a10 0,又 S21 a21 ,则可知 S20 0 ,则a1 a20 0 ,即a10 a11 0 ,故a11 0 ,
故S10 最小,D 错误.故选:BC.
考向四 等差数列片段和的性质
【例 4-1】(24-25 广西)已知等差数列 an 的前n 项和为 Sn ,且 S4 2, S8 6 ,则 S12 ( )
A.8 B.10 C.12 D.16
【答案】C
【解析】因为 an 是等差数列,所以 S4 , S8 S4 , S12 S 8 也是等差数列,
所以2 S8 S4 S12 S8 S4 ,即2 6 2 S12 6 2 ,解得 S12 12 .故选:C.
【例 4-2】(24-25 河南)已知等比数列 an 的前 n 项和为 Sn ,若 S6 7, S12 21 ,则 S24 ( )
A.56 B.105 C.112 D.189
【答案】B
【解析】因为 S6 , S12 S6 , S18 S12 , S24 S18成等比数列,
即7,14, S 21, S S 成等比数列,所以142 7 S 21 ,解得 S 49 ,
18 24 18 18 18
又14 S S S 21 2 ,所以14 S 49 49 21 2 ,解得S 105 .
24 18 18 24 24
故选:B.
【例 4-3】(23-24 甘肃 )设等差数列 a 的前n 项和为 S ,若 S14 7 ,则 S21 ( )
18 3
n n
7
11
S14
11
A. 7 B. 2 C. 7 D. 6
【答案】A
【解析】在等差数列 an 中, S7 , S14 S7 , S21 S14 成等差数列,则2 S14 S7 S7 S21 S14 ,
设S m ,则 S 7m ,故2 7m m m S 7m ,解得 S 18m ,所以 S21 18m 18 .故选:A.
7 14
21 21
S14 7m 7
【例 4-4】(2024 高三·全国·专题练习)设等差数列 an 的前n 项和为Sn ,若 S12 288, S9 162 ,则S6 ( )
A.18 B.36 C.54 D.72
【答案】D
【解析】因为差数列 an 中, S3 , S6 S3 , S9 S6 , S12 S9 成等差数列,
即 x 54 y, x 198 3y ,解得S6 y 72 ,故选:D.
【一隅三反】
1.(24-25 江西)已知等差数列 an 的前n 项和为 Sn ,若 S3 12 , S6 S3 24 ,则 S12 S9 ( )
A.36 B.48 C.60 D.120
【答案】B
【解析】由等差数列片段和的性质, S3 , S6 S3 , S9 S6 , S12 S9 成等差数列,【公众号:林樾数学】故S9 S6 2( S6 S3) S3 36,则 S12 S9 2(S9 S6 ) (S6 S3 ) 48 .故选:B
2.(24-25 四川)已知Sn 是等差数列 an 的前 n 项和,若 S20 15 , S40 40 ,则 S60 ( )
A.75 B.65 C.50 D.55
【答案】A
【解析】由等差数列前n 项和的性质得: S20 , S40 S20 , S60 S40 成等差数列,
2 S40 S20 S20 S60 S40,即2 40 15 15 S60 40 ,解得 S60 75 .故选:A.
3.(2024·河南周口·模拟预测)设 Sn 为等差数列 an 的前 n 项和,已知 S3 4, S6 10 ,则a16 a17 a18 ( )
A.12 B.14 C.16 D.18
【答案】B
【解析】由等差数列的片段和性质知, S3, S6 S3, S9 S6 , S12 S9 , S15 S12 , S18 S15
成等差数列,
由S3 4, S6 S3 6 ,得该数列首项为 4,公差为 2,所以a16 a17 a18 S18 S15 4 5 2 14 .故选:B 4.(2025·吉林长春·二模)已知等差数列 an 的前 n 项和为 Sn ,若 S3 S9 6 ,则 S12 的值为( )
A.0 B.3 C.6 D.12
【答案】A
【解析】因为 an 是等差数列,所以 S3 , S6 S3 , S9 S6 , S12 S9 成等差数列,
又S3 S9 6 ,所以6, S6 6, 6 S6 , S12 6成等差数列,则6 S12 6 S6 6 6 S6 ,则 S12 0 .故选:A. 5.(2025·四川)设等差数列 an 的前n 项和 Sn ,若 S3 9 , S6 36 ,则a7 a8 a9 ( )
A.18 B.27 C.45 D.63
【答案】C
【解析】由题意得 S3 , S6 S3 , S9 S6 成等差数列,即9, 36 9, a7 a8 a9 成等差数列,
即2 36 9 9 a7 a8 a9 ,解得a7 a8 a9 45 .故选:C
6.(24-25 河南·阶段练习)已知等差数列{a }的前n 项和为S ,若 S3 3 ,则 S12 ( )
n n
6 9
3 3 5
A. 7 B.3 C. 2 D. 3
【答案】C
【解析】由题意设 S3 3t ,则 S6 7t ,由{an }是等差数列,所以 S3, S6 S3, S9 S6 , S12 S9 , 也成等差数列,
所以 S S 2 7t 3t 3t 5t ,解得 S 12t ;S S 2 12t 7t 4t 6t ,解得 S 18t ,所以 S12 18t 3 ,
9 6
故选:C.【公众号:林樾数学】
9 12 9 12
考向五 等差数列和与 n 的比值
S9 12t 2
【例 5-1】(2025·江西)已知数列 a 和 b 都是等差数列,且其前 n 项和分别为S 和T ,若 Sn 3n 1 ,则 a5
n n
( )
16 28 10
n n 2n 5 b
34
A. 15 B. 23 C. 11 D. 27
【答案】B
【解析】对于等差数列的前 n 项和满足 S 2n 1 a ,知道 an S2n 1 ,故 a5 S9 3 9 1 28 .故选:B.
2n 1
n b T
b T 2 9 5 23
n 2n 1 5 9
【例 5-2】(24-25 四川)已知等差数列 a , b 的前n 项和分别为 S ,T ,若 Sn 2n ,则 a2 a8 ( )
n n n n
T 3n 1
b b
20 5
n 3 7
10 9
A. 31 B. 8 C. 13 D. 14
【答案】D
【解析】因为等差数列 an , bn 的前 n 项和分别为 Sn , Tn ,
9(a1 a9 )
所以我们对 a2 a8 进行变形,得到 a2 a8 a1 a9 2 S9 ,
b3 b7
b3 b7
b1 b9
9(b1 b9 ) T9
2
因为 Sn 2n ,所以 S9 18 9 ,即 a2 a8 9 ,故 D 正确.
Tn
故选:D
3n 1
T9 28 14
b3 b7 14
【例 5-3】(2025·黑龙江哈尔滨·模拟预测)已知Sn , Tn 分别是等差数列 an , bn 的前 n 项和,且
Sn 2n 1 n N* ,则 a3 a8 ( )
Tn 4n 2
b4 b7
b5 b6
7 11 21 17
A. 10 B. 18 C. 38 D. 30
【答案】C
【解析】因为 an , bn 是等差数列,
所以 a3
a8
10 a1 a10
a3 a8 a1 a10 2 S10
,又 Sn 2n 1 n N ,
b4 b7
b5 b6
b5 b6
b1 b10
10 b1 b10
2
T10
Tn 4n 2
a3
所以
b4 b7
a8 b5 b6
S10
T10
2 10 1 21 ,
4 10 2 38
故选:C.
【例 5-4】(2025·湖北·模拟预测)已知等差数列 a , b 的前 n 项和分别为 S ,T ,若 Sn n ,则 a5 ( )
n n
5 9 9
n n 2n 1 b
3
A. 9 B. 17 C. 20 D. 5
【答案】D
【解析】因为等差数列 a , b 的前 n 项和分别为 S , T ,所以 a5 S5 S4 ,
n n n n
b T T
4 4 3
因为 Sn
n
,所以可设S
kn2 , T
kn 2n 1 ,则 S S
9k , T T
15k ,所以 a5 9k
3 .
Tn
故选:D.
2n 1 n n
5 4 4 3
b4 15k 5
【例 5-5】(23-24 湖北武汉)在等差数列 a 中, a 1,其前 n 项和为 S ,若 S8 S6 2 ,则 S 等于( )
n 1 n 8 6 10
A.10 B.100 C.110 D.120
【答案】B
【解析】因为数列 a 是等差数列,则数列 Sn 也为等差数列,设其公差为d ,
n
则 S8 S6 2 2d ,则d 1,又因为 S1 a 1 ,所以 Sn 1 n 1 n ,所以 S n2 ,所以 S 100 .
8 6
故选:B.
1 1 n
n 10
【例 5-6】(23-24 高三上·河南·阶段练习)已知等差数列 a 的前 n 项和为 S ,且 S7 S3 4 ,则a a ( )
n n 7 3 9 6
A. 2 B. 3 C. 4 D. 6
【答案】D
【解析】设等差数列 an 的公差为d ,
n 1 a n n 1 d na n n 1
则 S S
1 1
d n n 1 d ,
n 1 n 2 2 a d a d
n 1
n n 1
n 1 2
1 2 2
数列 Sn 是公差为 d 的等差数列, S7 S3 4 d 4 ,解得: d 2 , a a 3d 6 .故选:D.
7 3 2 9 6
【一隅三反】
1.(24-25 高三上·河南·期末)已知 S 与T 分别是等差数列 a 与等差数列 b 的前 n 项和,且 Sn 6n ,
则 a1
b6 b2020
a2025 b4 b2022
n n
( )
Tn n 2025
A.1 B.2 C.3 D.4
【答案】C
【解析】由等差数列的性质可知b6 b2020 b4 b2022 b1 b2025 ,
所以 a1 a2025 a1 a2025 S2025 6 2025 3. 故选:C
b6 b2020 b4 b2022 b1 b2025 T2025 2025 2025
2.(2024·河北衡水·三模)已知数列 an , bn 均为等差数列,其前n 项和分别为Sn,Tn ,满足(2n 3)Sn (3n 1)Tn,则 a7 a8 a9 ( )
b6 b10
A.2 B.3 C.5 D.6
【答案】A
【解析】因为数列 a , b 均为等差数列,可得a a a 3a 1 15a 1 S ,
n n 7 8 9 8 5
8 5 15
1 S
且b b b b ,又由T 15 b1 b15 ,可得b b 2 T .因此 a7 a8 a9 5 3 S15 3 4 2 .
6 10 1 15
15 2
6 10
15 15
b b
2 2 T 2 3
故选:A.
6 10
15 T15 15
3.(2025 湖北)已知 S ,T 分别是等差数列 a , b 的前项和,且 Sn 2n 1 (n N* ) ,则 a10 a11 ( )
n n n n
T 4n 2
b b b b
21 23
n
43 41
3 18 6 15
A. 38 B. 42 C. 82 D. 78
【答案】D
【解析】 S ,T 分别是等差数列 a , b 的前项和,故 an S2n 1 (n N* ) ,且b b
b b
b b ,故
n n n n b T
3 18 6 15 10 11
n 2n 1
a10 a11 a10 a11 a10 a11 S20 2 20 1 41 ,
b3 b18
故选:D
b6 b15
b10 b11
b10 b11
b10 b11
T20
4 20 2 78
4.(24-25 高三上·宁夏银川·阶段练习)已知等差数列 a 和 b 的前 n 项和分别为 S ,T ,若 Sn 3n 4 ,则
a3 a8 ( )
b2 b9
n n n n
Tn n 2
17 37 37 17
A. 13 B. 13 C. 6 D. 6
【答案】D
10 a1 a10
【解析】因为数列 a 和 b 均为等差数列,所以 a3 a8 a1 a10 2 S10
3 10 4 17 .
n n b b b b 10 b b T
10 2 6
故选:D.
2 9 1 10
1 10 10
2
5.(2025·江苏)已知两个等差数列 a 和 b 的前 n 项和分别为 Sn 和 Tn,且 Sn = 2n 70 ,则 a7 的值为( )
n n
48 42 84
Tn n 3 b6
1
A. 7 B.
【答案】A
5 C. 9 D. 4
【解析】因为 Sn = 2n 70 ,所以可设 S kn 2n 70 , T
kn n 3 , k 0 ,
Tn n 3
所以a S S
588k 492k 96k , b T T
54k 40k 14k ,所以 a7 96k 48 ,故选:A.
7 7 6
6 6 5
b6 14k 7
6.(23-24 河北保定·期末)已知数列 a 满足a a 6 , a 的前n 项和为S ,则 S2024 S2022
( )
n n 1 n n
n 2024 2022
A.12 B. 6 C. 3 D. 2
【答案】B
【解析】 an 1 an 6 , 数列 an 是以6 为公差的等差数列,
n 1 a n n 1 6
na n n 1 6
Sn 1 Sn
2 1 2
a
3n
a 3 n
1 3 ,
n 1
n n 1
n 1 1
数列 Sn 是以3 为公差的等差数列, S2024 S2022 2 3 6 .
故选:B.
2024 2022
7.(2025·贵州)等差数列 a 的前n 项和为S ,若 S2021 S2020 1 且a 3 ,则( )
n n 2021 2020 1
A. an 2n 1 B. an n 1
C. S 2n2 n D. S 4n2 n
【答案】A
【解析】设 a 的公差为 d,∵ S na n n 1 d ∴ Sn a n 1 d d n a d ,即{ Sn }为等差数列,公差
n n 1 2
n 1 2 2 1 2 n
为 d ,由 S2021 S2020
1知 d 1 d 2 ,故a
2n 1,S
n 3 2n 1 n 2 2n
﹒故选:A﹒
2 2021 2020 2
n n 2
8.(2024 高三·全国·专题练习)已知 Sn 是等差数列{an}的前 n 项和,若 a1=﹣2018, S2019 S2013
2019 2013
6 ,则 S2020
等于( )
A.﹣4040 B.﹣2020 C.2020 D.4040
【答案】C
【解析】∵Sn 是等差数列{an}的前 n 项和,∴数列{ Sn }是等差数列.
n
∵a1=﹣2018, S2019 S2013 6 ,∴数列{ Sn }的公差 d 6 1 ,首项为﹣2018,∴ S2020
2018+2019×1=1,
2019 2013 n 6
∴S2020=2020.故选:C.
2020
考向六 等差数列的奇数项(偶数项)之和
【例 6-1】(2025 河南)一个等差数列共 100 项,其和为 80,奇数项和为 30,则该数列的公差为( )
1 1 2
A. 4 B.2 C. 3 D. 5
【答案】D
【解析】设等差数列的公差为d ,则由条件可知:数列的奇数项之和为a1 a3 a5 a99 30 ,①
偶数项之和为a2 a4 a6 a100 80 30 50 ,②
由②-①,得50d 20 ,所以d 2 ,即该数列的公差为 2 .
5 5
故选:D.
【例 6-2】(2025 陕西)等差数列 an
共 2n+1 个项,且奇数项和为 165,偶数项和为 150,则 n=( )
A.10 B.13 C.11 D.22
【答案】A
【解析】等差数列 an
共 2n+1 个项,其中奇数项有n 1个,偶数项有n 个,
设等差数列 a 的公差为d ,奇数项和a a
a
n 1 a n 1 n 2d
n 1 a nd 165 ①,
n 1 3 2 n 1 1 2 1
偶数项和a a
a
n a d n n 1 2d
n a nd 150 ②,
2 4 2 n 1 2 1
①-②得a1 nd 15 ,则n 15 150, n 10 .故选:A
【一隅三反】
1.(2023·重庆·二模)已知等差数列 an 的前 30 项中奇数项的和为A ,偶数项的和为 B ,且 B A 45 ,
2 A B 615 ,则an ( )
3n 2
3n 1
3n 1
3n 2
【答案】B
【解析】设等差数列的公差为d ,首项为a1 ,则 B A 15d 45 ,所以d 3,
因为2 A B 615 ,即2A A 45 615 ,则 A 660 ,
等差数列的奇数项是以a1 为首项, 2d 为公差的等差数列,等差数列 an 的前 30 项中奇数项有 15 项,所以
A 15a 15 14 6 660,得a 2 ,
1 2 1
所以an a1 n 1 d 2 3 n 1 3n 1.
故选:B
2.(2025 河南)已知等差数列 a 的公差d 1 , a a a
80 ,那么 S ( )
n 2 2 4 100
100
A.80 B.120 C.135 D.160
【答案】C
【解析】在等差数列 a 中,公差d 1 , a a a
80 ,
n 2 2 4 100
所以a a a a a
a 50d 80 50 1 55 ,
1 3 99 2 4
100 2
所以 S100 a1 a3 a99 a2 a4 a100 80 55 135 ,故选:C
3.(2025 上海)设等差数列的项数n 为奇数,则其奇数项之和与偶数项之和的比为( )
n 1
n
2n 1
n
2n 1
2n
n 1
n 1
【答案】D
【解析】由题知,奇数项有
n 1 2
项,偶数项有
n 1
项,
2
奇数项之和为 n 1 a
n 1 n 1
2 2
2 d n 1
n 1 d),
2 1 2 2
n 1 n 3
( a1 2
偶数项之和为 n 1 (a d ) 2 2
2d n 1 (a n 1 d ,
2 1 2 2 1 2
n 1
所以奇数项之和与偶数项之和的比为
故选:D
n 1 ,
考向七 等差数列的证明与判断
【例 6-1】(2025·全国一卷·高考真题)设数列 a 满足a 3 , an 1 an 1
,证明: na 为等差数列;
【答案】证明见解析
【解析】由题意证明如下, n N* ,
n 1 n n 1
n(n 1) n
在数列 a 中, a 3 , an 1 an
1 ,∴ n 1 a
na
1,即 n 1 a
na
1,
n 1 n n 1
n n 1
n 1 n
n 1 n
∴ nan 是以a1 3 为首项,1 为公差的等差数列.
【例 6-2】(2025·福建厦门·三模)已知数列 a 的前项和为 S ,a 1,且na S n2 n ,证明:数列 Sn
为等差数列;
n n 1
n 1 n
【答案】证明见解析;
【解析】由 S1 a1 1 , na
n(S
S ) S
n2 n ,则nS
(n 1) S
n(n 1),
1 1 n 1
n 1 n n
n 1 n
所以 Sn 1 Sn 1 ,故 Sn 是首项、公差均为 1 的等差数列;
n 1 n
【一隅三反】
1.(2025·江西新余·模拟预测)已知数列 a 的前n 项和为S , a
3S S
0 , a 1 .
1
n n n 1
n n 1 1 3
证明:数列
为等差数列;
n
求 an 的通项;
1
求 a 的最大值.
n
【答案】(1)证明见解析;
1 , n 1
3
an
1
3n n 1
;
, n 2
3.
【解析】(1)因为a
S S
,所以 S S
3S S ,故 1
1 3 ,
n 1
n 1 n
n n 1
n 1 n
Sn 1 Sn
又 1 1 3 ,所以 1 是以 3 为首项,3 为公差的等差数列.
S1 a1
n
1
(2)由(1)知
n
3 n 1 3 3n Sn
3n ,
当n 2 时, a
3 1 1
1 ,
n 3n 3n 3
3n n 1
而n 1 时, a 1 不满足题意,
n 3
1 , n 1
3
所以an
1
3n n 1
.
, n 2
1
(3)由(2)知,当n 2 时,
n
3n n 1 0 ,
又 1 3 0 ,所以, 1 的最大值为 1 3.
a a a
1 n 1
2.(24-25 高三下·甘肃庆阳·期中)记 Sn 为正项数列 an 的前n 项和,且a1Sn n 1 an .
(1)求a1 的值;
(2)判断 an 是否为等差数列,并求 a 的通项公式;
【答案】(1) a1 2
(2) an 是常数列,也是等差数列, a
n
n
2n .
【解析】(1)令 n 1 可得a2 2a , 又a 0 ,故a 2 .
1 1 1 1
(2) 2Sn n 1 an ,① 2Sn 1 n 2 an 1 ,②
由②-①,得2a n 2 a n 1 a ,即na n 1 a 故 an 1 an ,故 an 是常数列,也是等差数列
n 1
故 an a1 2 ,故a
2n .
n 1
n n 1
n n 1 n
n 1 n
3.(2025·河南许昌·三模)在数列 an 中, a1 0, a2 4 ,且an 2 2an 1 an 2 ,证明: an 1 an 是等差数列;
【答案】证明见解析
【解析】 在数列 an 中, a1 0, a2 4 ,且an 2 2an 1 an 2 ,
a 2 an 1 an 1 an 2a 1 a 2 an 1 a 1 an 2 ,
an 1 an 是首项为a2 a1 4 ,公差为 2 的等差数列.
4.(2025·甘肃白银·模拟预测)已知数列 a 满足a 2 , a
an ,
n为奇数,数列 b 满足b a .
n 1 n 1
a 1, n为偶数
n n 2n 1
n
(1)证明:数列 bn 为等差数列;
(2)求数列 bn 的通项公式及前 n 项和 Sn ;
【答案】(1)证明见解析
(2) bn
n 1
, Sn
n2 3n 2
【解析】(1) bn 1 bn a2n 1 a2n 1 a2n 1 a2n 1 1 ,
所以数列 bn 为等差数列,首项为b1 a1 2 ,公差为 1.
(2) bn
2 n 1 1 n 1
, Sn
2 n 1 n n2 3n
2 2
考向八 含绝对值的等差数列的前 n 项和
【例 7-1】(23-24 高三上·贵州·阶段练习)记等差数列 an 的前n 项和为Sn ,已知a1 11, S3 S9 .
(1)求 an 的通项公式;
(2)记数列 an 的前n 项和为Tn ,求T100 .
【答案】(1) an 2n 13 (2)8872
【解析】(1)由 S3 S9 a4 a5 a6 a7 a8 a9
0 a6 a7
0 则a12 a1 11
设 an 的公差为d 则a1 11d 11 11 11d 11 d 2 则an a1 n 1 d 11 2 n 1 2n 13
所以数列 an 的通项公式为an 2n 13 .
(2)由题可知T100 a1 a2 a6 a7 a100 T100 a1 a2 a6 a7 a100
T S
S
S 2S S
2 6 11 1 100 11 187 8872 , T
8872 .
100 6 100 6 6 100 2 2
100
【例 7-2】(24-25 高三上·湖北·开学考试)已知数列 an 的前n 项和为 Sn ,且a1 2, an 1 Sn 2 .
(1)求数列 an 的通项公式;
(2)设b
log a2 11,求数列 b 的前n 项和T .
【答案】(1) a 2n , n N*
10n n2 , n 5
(2) Tn n2 10n 50, n 6
, n N* .
【解析】(1)由 an 1 Sn 2 ,则当n 2 时an Sn 1 2
两式相减得an 1 an an ,所以an 1 2an n 2 .将a1 2 代入an 1 Sn 2 得, a2 4 2a1,所以对于n N*, a 2a ,故 a 是首项为 2,公比为 2 的等比数列,所以a 2n .
(2) b log a 2 11 2n 11 . B b b b
n n 10 n2 10n ,
n 2 n n 1 2 n
因为当n 5 时b 0 ,当n 6 时b 0 ,所以当 n 5时, T b b b B
10n n 2 ,
n n n 1 2 n n
当n 6 时, T
b b
b b b
b
B 2B
n 2 10n 50 .故T
10n n2 , n 5
.
n
【一隅三反】
1 2 5 6 7
n n 5
n n2 10n 50, n 6
1.(2024·全国·模拟预测)已知等差数列 an , a1 10 ,记 Sn 为 an 的前n 项和,从下面①②③中再选取一
个作为条件,解决下面问题.① 2a a 0;② S 55 ;③ S7 S5 2 .
5 8 11 7 5
(1)求Sn 的最小值;
(2)设 an 的前n 项和为Tn ,求T20 .
【答案】(1)答案见解析
(2)答案见解析
【解析】(1)设等差数列 an 的公差为d ,且a1 10 .
选择①:(1)因为2a5 a8 0,所以3a1 15d 0 ,解得d 2 .
所以a a (n 1)d 2n 12 ,则 S na n(n 1) d n2 11 n,
n 1 n 1 2
利用二次函数对称性和开口方向知, S n2 11n 关于 n 5.5 对称,
因为n N* ,所以当n 5 或 6 时, Sn S5 S 6 30 .
选择②:因为S 55 ,可得11 (a1 a11) 55 ,
11 2
因为a 10 ,所以a 0 ,此时d a11 a1 1 ,所以a a (n 1)d n 11 ,
1 11
11 1 n 1
因为d 0 ,所以 an 单调递增,且当n 11时, an 0 .
所以当n 10 或 11 时, Sn 最小,此时 Sn S10 S11 55 .
选择③:因为 S7 S5 2 ,所以 a1 a7 a1 a5 2 ,即a a 4 ,所以d a7 a5 2 ,
7 5 2 2 7 5 2
所以a a (n 1)d 2n 12 ,则 S na n(n 1) d n2 11 n,
n 1 n 1 2
利用二次函数对称性和开口方向知, S n2 11n 关于 n 5.5 对称,【公众号:林樾数学】因为n N* ,所以当n 5 或 6 时, Sn S5 S 6 30 .
(2)解:若选择①或③:由(1)知an 2n 12 ,当n 6 时, an 0 ,
所以T20 a1 a2 a3 a20 a1 a2 a3 a3 a5 a6 a7 a20
T20 a1 a2 a3 a20 2( a1 a2 a3 a3 a5) S20 2S5 240 .
若选择②:由(1)知an
n 11,且当n 11时, an 0 ,且 Sn
1 n 2 21 n ,
2 2
所以T20 a1 a2 a3 a20 a1 a2 a10 a11 a12 a20
T20 a1 a2 a3 a20 2( a1 a2 a3 a10) S20 2S10 100 .
2(2023·全国乙卷·高考真题)记 Sn 为等差数列 an 的前n 项和,已知a2 11, S10 40 .
(1)求 an 的通项公式;
(2)求数列 an 的前n 项和Tn .
【答案】(1) an 15 2n
14n n2 , n 7
(2) Tn n2 14n 98, n 8
【解析】(1)设等差数列的公差为 d ,
a2 a1 d 11
a1 d 11
a1
13
由题意可得 S 10a 10 9 d 40 ,即 2a 9d 8 ,解得 d 2 ,
10 1 2 1
所以an 13 2 n 1 15 2n ,
n 13 15 2n 2
(2)因为 Sn
14n n ,
2
令an
15 2n 0 ,解得n 15 ,且n N* ,
2
当n 7 时,则a 0 ,可得T a a a a a a S 14n n2 ;
n n 1 2 n 1 2 n n
当n 8 时,则an 0 ,可得Tn a1 a2 an a1 a2 a7 a8 an
S S S 2S S 2 14 7 7 2 14n n 2 n 2 14n 98 ;【公众号:林樾数学】
14n n2 , n 7
综上所述: Tn n2 14n 98, n 8 .
考向九 等差数列的简单应用
【例 8-1】(23-24 高三下·重庆渝中·阶段练习)中国载人航天工程发射的第十八艘飞船,简称“神十八”,于 2024年 4 月执行载人航天飞行任务.运送“神十八”的长征二号F运载火箭,在点火第一秒钟通过的路程为2km ,以后每秒钟通过的路程都增加3km ,在达到离地面222km的高度时,火箭开始进入转弯程序.则从点火到进入转弯程序大约需要的时间是( )秒.
A.10 B.11 C.12 D.13
【答案】C
【解析】设出每一秒钟的路程为数列{an },由题意可知{an }为等差数列,
则数列首项a1 2 ,公差d 3,所以an a1 n 1 d 2 n 1 3 3n 1,
由求和公式有 Sn
n a1 an (3n 1 2)n 222 ,解得n 12 ,故选:C.
2 2
【例 8-2】(24-25 山东 )“中国剩余定理”又称“孙子定理”,原文如下:今有物不知其数,三三数之剩二(除以 3
余 2),五五数之剩三(除以 5 余 3),七七数之剩二(除以 7 余 2),问物几何?现有这样一个相关的问题:已知正整数 p( p 1) 满足二二数之剩一,三三数之剩一,将符合条件的所有正整数 p 按照从小到大的顺序排成一列,构
成数列 a ,记数列 a 的前 n 项和为 S ,则 2Sn an 23 的最小值为( )
n n n n
A.26 B.36 C.38 D.46
【答案】C
【解析】二二数之剩一、三三数之剩一的数分别为2m 1、3k 1, m,k N ,
因此数列{an }的项即为以上两类数的公共项6n 1,即an 6n 1, n N ,而an 1 an (6 n 7) (6 n 1) 6,则数列{an }是等差数列,
n(7 6n 1) 2
2S a 23 6n2 14n 24 4
于是 Sn 2 3n
4n , n n 6(n
n n n
) 14 ,
又对勾函数 y x 4 在(0, 2] 上单调递减,在[2, ) 上单调递增,
x
所以n 2 时, 2Sn an 23 取得最小值 38.故选:C
n
【一隅三反】
1.(2024·广东广州·模拟预测)元代数学家朱世杰编著的《算法启蒙》中记载了有关数列的计算问题:“今有竹七节,下两节容米四升,上两节容米二升,各节欲均容,问逐节各容几升?”其大意为:现有一根七节的竹子,最下面两节可装米四升,最上面两节可装米二升,如果竹子装米量逐节等量减少,问竹子各节各装米多少升?以此计算,这根竹子的装米量为( )
A. 9 升 B.10.5 升 C.12 升 D.13.5 升
【答案】B
【解析】依题意,竹子自下而上的各节装米量构成等差数列{a }, n N , n 7 ,则a1 a2 4, a6 a7 2 , a1 a7 a2 a6 3 ,
所以这根竹子的装米量为S7
故选:B
7(a1 a7 ) 10.5 (升).【公众号:林樾数学】
2
2.(2025 江西抚州·期中)我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度),二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是( )
A.相邻两个节气晷长减少或增加的量为十寸 B.秋分的晷长为 75 寸
C.立秋的晷长比立春的晷长长 D.立冬的晷长为一丈五寸
【答案】C
【解析】由题意可知夏至到冬至的晷长构成等差数列 an ,其中a1 15 寸, a13 135 寸,公差为d 寸,则
135 15 12d ,解得d 10 (寸),
同理可知由冬至到夏至的晷长构成等差数列 bn ,首项b1 135 ,末项b13 15 ,公差d 10 (单位都为寸).故选项 A 正确;
春分的晷长为b7 , b7 b1 6d 135 60 75,
秋分的晷长为a7 , a7 a1 6d 15 60 75,所以B 正确;
立冬的晷长为a10 , a10 a1 9d 15 90 105 ,即立冬的晷长为一丈五寸, D 正确;
立春的晷长,立秋的晷长分别为b4 , a4 ,【公众号:林樾数学】
a4 a1 3d 15 30 45, b4 b1 3d 135 30 105, b4 a4 ,故错C 误.故选:C.
3.(2023·四川达州·一模)《孙子算经》是我国南北朝时著名的数学著作,其中有物不知数问题:今有物不知
其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?意思是:有一些物品,不知道有多少个,只知道将它们三个三个地数,会剩下 2 个;五个五个地数,会剩下 3 个;七个七个地数,也会剩下 2 个.这些物品
的数量是多少个?若一个正整数除以三余二,除以五余三,将这样的正整数由小到大排列,则前 5 个数的和为
( )
A.189 B.190 C.191 D.192
【答案】B
【解析】根据题意,被以 3 除余 2,除以 5 余 3 的数,构成首项为8 ,公差为15 的等差数列,
则an 8 (n 1) 15 15n 7,
所以将这样的正整数由小到大排列,则前 5 个数的和为故选:B.
5 8 15 5 7
2
190 .
考向一 等差数列基本量的计算
【例 1-1】(2025·山东德州·三模)已知Sn 为等差数列 an 的前n 项和, a2 4, S5 3a4 6 ,则a8 ( )
B.8 C.16 D.32
【例 1-2】(2025·广西柳州·模拟预测)设等差数列 an 的前n 项和为 Sn ,若 S4 S1 9, a1 a4 5 ,则 an 的公差为( )
A.1 B.2 C.3 D.4
【例 1-3】(2025·湖北黄冈·模拟预测)设等差数列 an 的前n 项和为 Sn ,若Sm 3, Sm 1 0, Sm 2 4 ,则m ( )
A.8 B.7 C.6 D.5
【一隅三反】【公众号:林樾数学】
1.(2025·北京·高考真题)已知 an 是公差不为零的等差数列, a1 2 ,若a3 , a4 , a6 成等比数列,则a10 ( )
20
18
C.16 D.18
2.(2025·福建·模拟预测)已知 Sn 为等差数列 an 的前n 项和,若 a3 S3 2 , a4 S4 6 ,则 S9 ( )
A.28 B.32 C.36 D.40
3.(2025·黑龙江大庆·模拟预测)已知等差数列 an 的前n 项和为 Sn ,若S5 2S3 , a1 a8 10 ,则公差d 为( )
1 1 2
A. 4 B. 2 C. 3 D.1
4.(2025·浙江·三模)设等差数列 an 的前 n 项和为 Sn ,已知a2 3 , S5 25 ,则a3 2a6 ( )
5.(2025·山西·二模)已知等差数列{an }公差不为 0,记其前 n 项和为 Sn ,若a6 a5 a7 , S2k a2k ,则正整数 k
的值为( )
B.6 C.8 D.12
考向二 等差中项及应用
【例 2-1】(2026 高三·全国·专题练习)若a 是 1 和 3 的等差中项, b 是 1 和 4 的等比中项,则 a 的值为( )
b
1
2
1
2
C.1 D. 1
【例 2-2】(2025·宁夏银川·二模)已知等差数列 an 的前 n 项和为 Sn ,且a2 a4 6 ,则 S5 ( )
A.0 B.10 C.15 D.30
【例 2-3】(2025·广西·三模)在公差不为 0 的等差数列 a 中,若a 是a 与a 的等差中项,则 1 4 的最小值
为( )
3 5
n 3 x y x y
6 9
A. 2 B. 3 C. 5 D. 5
【例 2-4】(2025·山东·一模)已知(1 2x)n n N* 的展开式中第 2 项,第 3 项,第 4 项的二项式系数成等差数列,则n ( )
A.5 B.6 C.7 D.8
【一隅三反】
1.(2025·辽宁·一模)已知等差数列 an 的前n 项和为Sn ,若a3 a10 a6 4 ,则 S13 ( )
B.60 C.68 D.52
2.(23-24 浙江)在V ABC 中,三个内角 A, B,C 成等差数列,则sin A C ( )
1
A. 2
B. 2
2
C. 3
2
D.1
3.(2025·广东汕头·模拟预测)已知a, b R , b 为a 和2 的等差中项,则3a 1 的最小值为( )
9b
1 1 2
A. 3 B. 2 C. 2 D. 3
4(2025·安徽淮北·二模)若实数m 和n 的等差中项为 1,则m2 n2 的最小值为 .
考向三 等差数列前 n 项和最值
【例 3-1】(2025·广西南宁·三模)设等差数列 an 的前 n 项和为 Sn ,若a5 2 , a3 a8 12 a7 ,则 Sn 的最小值
为( )【公众号:林樾数学】
A. 14
B. 49
4
C. 12
D. 10
时n 的值为( )
A.12 B.13 C.14 D.25
【例 3-3】(24-25 高三下·云南昭通·阶段练习)已知数列{an }是等差数列,其前 n 项和为 Sn ,若a3 a10 0 ,S11 0 ,则数列{Sn } 中最小的项是( )
S4
S5
S6
S7
【一隅三反】
1.(2025·江西·模拟预测)记 Sn 为等差数列 an 的前 n 项和,且a2 2a1 2 ,则满足 Sn 888的 n 的最大值为
( )
A.40 B.41 C.42 D.43
2.(24-25 陕西西安·期末)设等差数列 an 的前n 项和为Sn ,若a5 a8 0 , S11 0 ,则 Sn 的最大值为( )
A. S5
B. S6
C. S7
D. S8
3.(2025·山东泰安·模拟预测)公差不为0 的等差数列 an 的前n 项和为 Sn ,若a7 2 , a9 , a5 , a13 成等比数列,则满足Sn 0 的n 的最大值为( )
A. 8 B. 9 C.13 D.14
4.(2025·甘肃金昌·模拟预测)(多选)许多已知等差数列 an 的公差d 0 ,其前 n 项和记为 Sn , a1 0 ,则下列说法正确的是( )
A.数列 an 中有最大项 B.数列 Sn 中有最小项
C.若a a 0 ,则 55 S10 45
D.若 S
a , S
a ,则 S 取最小值时n 9
10 11 d
20 20
21 21 n
考向四 等差数列片段和的性质
【例 4-1】(24-25 广西)已知等差数列 an 的前n 项和为 Sn ,且 S4 2, S8 6 ,则 S12 ( )
A.8 B.10 C.12 D.16
【例 4-2】(24-25 河南)已知等比数列 an 的前 n 项和为 Sn ,若 S6 7, S12 21 ,则 S24 ( )
A.56 B.105 C.112 D.189
【例 4-3】(23-24 甘肃 )设等差数列 a 的前n 项和为 S ,若 S14 7 ,则 S21 ( )
18 3
n n
7
11
S14
11
A. 7 B. 2 C. 7 D. 6
【例 4-4】(2024 高三·全国·专题练习)设等差数列 an 的前n 项和为Sn ,若 S12 288, S9 162 ,则S6 ( )
A.18 B.36 C.54 D.72
【一隅三反】
1.(24-25 江西)已知等差数列 an 的前n 项和为 Sn ,若 S3 12 , S6 S3 24 ,则 S12 S9 ( )
A.36 B.48 C.60 D.120
2.(24-25 四川)已知Sn 是等差数列 an 的前 n 项和,若 S20 15 , S40 40 ,则 S60 ( )
A.75 B.65 C.50 D.55
3.(2024·河南周口·模拟预测)设 Sn 为等差数列 an 的前 n 项和,已知 S3 4, S6 10 ,则a16 a17 a18 ( )
A.12 B.14 C.16 D.18
4.(2025·吉林长春·二模)已知等差数列 an 的前 n 项和为 Sn ,若 S3 S9 6 ,则 S12 的值为( )
A.0 B.3 C.6 D.12
5.(2025·四川)设等差数列 an 的前n 项和 Sn ,若 S3 9 , S6 36 ,则a7 a8 a9 ( )
A.18 B.27 C.45 D.63
6.(24-25 河南·阶段练习)已知等差数列{a }的前n 项和为S ,若 S3 3 ,则 S12 ( )
n n
6 9
3 3 5
A. 7 B.3 C. 2 D. 3
考向五 等差数列和与 n 的比值
【例 5-1】(2025·江西)已知数列 a 和 b 都是等差数列,且其前 n 项和分别为S 和T ,若 Sn 3n 1 ,则 a5
n n
( )
16 28 10
n n 2n 5 b
34
A. 15 B. 23 C. 11 D. 27
【例 5-2】(24-25 四川)已知等差数列 a , b 的前n 项和分别为 S ,T ,若 Sn 2n ,则 a2 a8 ( )
n n n n
T 3n 1
b b
20 5
n 3 7
10 9
A. 31 B. 8 C. 13 D. 14
【例 5-3】(2025·黑龙江哈尔滨·模拟预测)已知Sn , Tn 分别是等差数列 an , bn 的前 n 项和,且
Sn 2n 1 n N* ,则 a3 a8 ( )
Tn 4n 2
7
b4 b7
11
b5 b6
21 17
A. 10 B. 18 C. 38 D. 30
【例 5-4】(2025·湖北·模拟预测)已知等差数列 a , b 的前 n 项和分别为 S ,T ,若 Sn n ,则 a5 ( )
n n
5 9 9
n n 2n 1 b
3
A. 9 B. 17 C. 20 D. 5
【例 5-5】(23-24 湖北武汉)在等差数列 a 中, a 1,其前 n 项和为 S ,若 S8 S6 2 ,则 S 等于( )
n 1 n 8 6 10
A.10 B.100 C.110 D.120
【例 5-6】(23-24 高三上·河南·阶段练习)已知等差数列 a 的前 n 项和为 S ,且 S7 S3 4 ,则a a ( )
n n 7 3 9 6
A. 2 B. 3 C. 4 D. 6
【一隅三反】
1.(24-25 高三上·河南·期末)已知 S 与T 分别是等差数列 a 与等差数列 b 的前 n 项和,且 Sn 6n ,
则 a1
b6 b2020
a2025 b4 b2022
n n
( )
Tn n 2025
A.1 B.2 C.3 D.4
2.(2024·河北衡水·三模)已知数列 an , bn 均为等差数列,其前n 项和分别为Sn,Tn ,满足(2n 3)Sn (3n 1)Tn,则 a7 a8 a9 ( )
b6 b10
A.2 B.3 C.5 D.6
3.(2025 湖北)已知 S ,T 分别是等差数列 a , b 的前项和,且 Sn 2n 1 (n N* ) ,则 a10 a11 ( )
n n n n
T 4n 2
b b b b
21 23
n
43 41
3 18 6 15
A. 38 B. 42 C. 82 D. 78
4.(24-25 高三上·宁夏银川·阶段练习)已知等差数列 a 和 b 的前 n 项和分别为 S ,T ,若 Sn 3n 4 ,则
a3 a8 ( )
b2 b9
n n n n
Tn n 2
17 37 37 17
A. 13 B. 13 C. 6 D. 6
5.(2025·江苏)已知两个等差数列 a 和 b 的前 n 项和分别为 Sn 和 Tn,且 Sn = 2n 70 ,则 a7 的值为( )
n n
48 42 84
Tn n 3 b6
1
A. 7 B. 5 C. 9 D. 4
6.(23-24 河北保定·期末)已知数列 a 满足a a 6 , a 的前n 项和为S ,则 S2024 S2022 ( )
n n 1 n n
n 2024 2022
A.12 B. 6 C. 3 D. 2
7.(2025·贵州)等差数列 a 的前n 项和为S ,若 S2021 S2020 1 且a 3 ,则( )
n n 2021 2020 1
A. an 2n 1 B. an n 1
C. S 2n2 n D. S 4n2 n
8.(2024 高三·全国·专题练习)已知 Sn 是等差数列{an}的前 n 项和,若 a1=﹣2018, S2019 S2013
2019 2013
6 ,则 S2020
等于( )
A.﹣4040 B.﹣2020 C.2020 D.4040
考向六 等差数列的奇数项(偶数项)之和
【例 6-1】(2025 河南)一个等差数列共 100 项,其和为 80,奇数项和为 30,则该数列的公差为( )
1 1 2
A. 4 B.2 C. 3 D. 5
【例 6-2】(2025 陕西)等差数列 an 共 2n+1 个项,且奇数项和为 165,偶数项和为 150,则 n=( )
A.10 B.13 C.11 D.22
【一隅三反】
1.(2023·重庆·二模)已知等差数列 an 的前 30 项中奇数项的和为A ,偶数项的和为 B ,且 B A 45 ,
2 A B 615 ,则an ( )
3n 2
3n 1
3n 1
3n 2
2.(2025 河南)已知等差数列 a 的公差d 1 , a a a 80 ,那么 S ( )
n 2 2 4 100
100
A.80 B.120 C.135 D.160
3.(2025 上海)设等差数列的项数n 为奇数,则其奇数项之和与偶数项之和的比为( )
n 1
n
2n 1
n
2n 1
2n
n 1
n 1
考向七 等差数列的证明与判断
【例 6-1】(2025·全国一卷·高考真题)设数列 a 满足a 3 , an 1 an 1 ,证明: na 为等差数列;
n 1 n n 1 n(n 1) n
【例 6-2】(2025·福建厦门·三模)已知数列 a 的前项和为 S ,a 1,且na S n2 n ,证明:数列 Sn
为等差数列;
n n 1
n 1 n
【一隅三反】
1.(2025·江西新余·模拟预测)已知数列 a 的前n 项和为S , a 3S S 0 , a 1 .
1
n n n 1
n n 1 1 3
证明:数列
为等差数列;
n
求 an 的通项;
1
求 a 的最大值.
n
2.(24-25 高三下·甘肃庆阳·期中)记 Sn 为正项数列 an 的前n 项和,且a1Sn n 1 an .
求a1 的值;
判断 an 是否为等差数列,并求 a 的通项公式;
n
4.(2025·甘肃白银·模拟预测)已知数列 a 满足a 2 , a an , n为奇数,数列 b 满足b a .
n 1 n 1
a 1, n为偶数
n n 2n 1
n
证明:数列 bn 为等差数列;
求数列 bn 的通项公式及前 n 项和 Sn ;
考向八 含绝对值的等差数列的前 n 项和
【例 7-1】(23-24 高三上·贵州·阶段练习)记等差数列 an 的前n 项和为Sn ,已知a1 11, S3 S9 .
求 an 的通项公式;
记数列 an 的前n 项和为Tn ,求T100 .
【例 7-2】(24-25 高三上·湖北·开学考试)已知数列 an 的前n 项和为 Sn ,且a1 2, an 1 Sn 2 .
求数列 an 的通项公式;
设b
log a2 11,求数列 b 的前n 项和T .【公众号:林樾数学】
【一隅三反】
1.(2024·全国·模拟预测)已知等差数列 an , a1 10 ,记 Sn 为 an 的前n 项和,从下面①②③中再选取一
个作为条件,解决下面问题.① 2a a 0;② S 55 ;③ S7 S5 2 .
5 8 11 7 5
求Sn 的最小值;
设 an 的前n 项和为Tn ,求T20 .
2(2023·全国乙卷·高考真题)记 Sn 为等差数列 an 的前n 项和,已知a2 11, S10 40 .
求 an 的通项公式;
求数列 an 的前n 项和Tn .
考向九 等差数列的简单应用
【例 8-1】(23-24 高三下·重庆渝中·阶段练习)中国载人航天工程发射的第十八艘飞船,简称“神十八”,于 2024年 4 月执行载人航天飞行任务.运送“神十八”的长征二号F运载火箭,在点火第一秒钟通过的路程为2km ,以后每秒钟通过的路程都增加3km ,在达到离地面222km的高度时,火箭开始进入转弯程序.则从点火到进入转弯程序大约需要的时间是( )秒.【公众号:林樾数学】
A.10 B.11 C.12 D.13
【例 8-2】(24-25 山东 )“中国剩余定理”又称“孙子定理”,原文如下:今有物不知其数,三三数之剩二(除以 3余 2),五五数之剩三(除以 5 余 3),七七数之剩二(除以 7 余 2),问物几何?现有这样一个相关的问题:已知正整数 p( p 1) 满足二二数之剩一,三三数之剩一,将符合条件的所有正整数 p 按照从小到大的顺序排成一列,构
成数列 a ,记数列 a 的前 n 项和为 S ,则 2Sn an 23 的最小值为( )
n n n n
A.26 B.36 C.38 D.46
【一隅三反】
1.(2024·广东广州·模拟预测)元代数学家朱世杰编著的《算法启蒙》中记载了有关数列的计算问题:“今有竹七节,下两节容米四升,上两节容米二升,各节欲均容,问逐节各容几升?”其大意为:现有一根七节的竹子,最下面两节可装米四升,最上面两节可装米二升,如果竹子装米量逐节等量减少,问竹子各节各装米多少升?以此计算,这根竹子的装米量为( )
A. 9 升 B.10.5 升 C.12 升 D.13.5 升
2.(2025 江西抚州·期中)我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度),二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是( )
A.相邻两个节气晷长减少或增加的量为十寸 B.秋分的晷长为 75 寸
C.立秋的晷长比立春的晷长长
D.立冬的晷长为一丈五寸【公众号:林樾数学】
3.(2023·四川达州·一模)《孙子算经》是我国南北朝时著名的数学著作,其中有物不知数问题:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?意思是:有一些物品,不知道有多少个,只知道将它们三个三个地数,会剩下 2 个;五个五个地数,会剩下 3 个;七个七个地数,也会剩下 2 个.这些物品
的数量是多少个?若一个正整数除以三余二,除以五余三,将这样的正整数由小到大排列,则前 5 个数的和为
( )
A.189 B.190 C.191 D.192
等差数列(精讲精练)解析版
考向一 等差数列基本量的计算
【例 1-1】(2025·山东德州·三模)已知Sn 为等差数列 an 的前n 项和, a2 4, S5 3a4 6 ,则a8 ( )
B.8 C.16 D.32
【答案】C
【解析】设等差数列 a 的公差为d ,由题意得 a1 d 4
,解得 a1 2 ,所以a a 7d 16 .
5a1 10d 3a1 9d 6
d 2 8 1
故选:C
【例 1-2】(2025·广西柳州·模拟预测)设等差数列 an 的前n 项和为 Sn ,若 S4 S1 9, a1 a4 5 ,则 an 的公差为( )
A.1 B.2 C.3 D.4
【答案】A
【解析】因为 S4 S1 9, a1 a4 5 ,所以a2 a3 a4 3a3 9 ,解得a3 3,又a1 a4 a2 a3 5 ,所以a2 2 ,所以公差为a3 a2 1.故选:A.
【例 1-3】(2025·湖北黄冈·模拟预测)设等差数列 an 的前n 项和为 Sn ,若Sm 3, Sm 1 0, Sm 2 4 ,则m ( )
A.8 B.7 C.6 D.5
【答案】C
【解析】方法一:由题意得: am 1 Sm 1 Sm 3 , am 2 Sm 2 Sm 1 4 ,
则等差数列的公差d am 2
am 1
1,则a1
3 m , Sm
m 3 m m m 1 3,所以m 6 .
2
方法二:因为等差数列的性质即 Sn 为等差数列,则 Sm Sm 2 2Sm 1 ,得 3 4 0 ,解得m 6 .
故选:C
【一隅三反】
m m 2
m 1
m m 2
1.(2025·北京·高考真题)已知 an 是公差不为零的等差数列, a1 2 ,若a3 , a4 , a6 成等比数列,则a10 ( )
20
18
C.16 D.18
【答案】C
【解析】设等差数列 an 的公差为d , d 0 ,
因为a , a , a 成等比数列,且a 2 ,所以a2 a a
,即 2 3d 2 2 2d 2 5d ,解得d 2 或d 0 (舍
去),所以a10 a1 9d 2 9 2 16.故选:C.
2.(2025·福建·模拟预测)已知 Sn 为等差数列 an 的前n 项和,若 a3 S3 2 , a4 S4 6 ,则 S9 ( )
A.28 B.32 C.36 D.40
【答案】C
【解析】设等差数列 an 的公差为d ,因为a3 S3 2 , a4 S4 6 ,故两式作差可得:
a a S S 4 ,即d a 4 , a 4 ,又 S 9 a1 a9 9a ,故 S 36 .
4 3 4 3
故选:C.
4 5 9 2 5 9
3.(2025·黑龙江大庆·模拟预测)已知等差数列 an 的前n 项和为 Sn ,若S5 2S3 , a1 a8 10 ,则公差d 为( )
1 1 2
A. 4 B. 2 C. 3 D.1
【答案】C
【解析】由S 2S ,则 5(a1 a5 ) 2 3(a1 a3 ) ,即5a 6a ,所以5(a d ) 6a 5d a ,则a 4d ,
5 3 2 2
3 2 2 2 2 1
由a a 2a 7d 15d 10 ,则 d 2 .故选:C
1 8 1 3
4.(2025·浙江·三模)设等差数列 an 的前 n 项和为 Sn ,已知a2 3 , S5 25 ,则a3 2a6 ( )
A.17 B.21 C.23 D.27
【答案】D
【解析】设等差数列 a 的公差为d ,由题意得 a1 d 3 ,解得 a1 1,所以a 2a 3a 12d 27 .故
5a1 10d 25
d 2
3 6 1
选:D.
5.(2025·山西·二模)已知等差数列{an }公差不为 0,记其前 n 项和为 Sn ,若a6 a5 a7 , S2k a2k ,则正整数 k
的值为( )
B.6 C.8 D.12
【答案】B
【解析】设等差数列{an }公差为d , d 0 ,由a6 a5 a7 ,得a6 2a6 ,解得a6 0 ,
a a 5d 5d , a a (n 1)d (n 6)d , S 5d (2k 6)d 2k ,
1 6 n 1
2k 2
因此 5d (2k 6)d 2k (2k 6)d ,整理得2k 2 13k 6 0 ,解得k 6 .故选:B
2
考向二 等差中项及应用
【例 2-1】(2026 高三·全国·专题练习)若a 是 1 和 3 的等差中项, b 是 1 和 4 的等比中项,则 a 的值为( )
b
1
2
【答案】D
1
2
C.1 D. 1
【解析】由题知2a 1 3 ,所以a 2 ,由b2 4 得b 2 ,所以 a 1 .故选:D.
b
【例 2-2】(2025·宁夏银川·二模)已知等差数列 an 的前 n 项和为 Sn ,且a2 a4 6 ,则 S5 ( )
A.0 B.10 C.15 D.30
【答案】C
【解析】因为a a 6, 所以2a 6, a
3. 又因为 S
5 a1 a5 5a
15, 故选:C.
2 4 3 3
5 2 3
【例 2-3】(2025·广西·三模)在公差不为 0 的等差数列 a 中,若a 是a 与a 的等差中项,则 1 4 的最小值
为( )
3 5
n 3 x y x y
6 9
A. 2 B. 3 C. 5 D. 5
【答案】A
【解析】因为在公差不为 0 的等差数列 an 中, a3 是ax 与ay 的等差中项,所以2a3 ax ay ,所以 x y 6 ,
1 4 1 x y
1 4 1 5 y 4 x 1
2 3
y 4x
y 4
所以
x y 6
x y 6
x y
6 5
2
,当且仅当 x y
,即 x 2 ,
时等号
成立,所以 1 4 的最小值为 3 .故选: A .
x y 2
【例 2-4】(2025·山东·一模)已知(1 2x)n n N* 的展开式中第 2 项,第 3 项,第 4 项的二项式系数成等差数列,则n ( )
A.5 B.6 C.7 D.8
【答案】C
【解析】已知(1 2x)n n N* 的展开式中第 2 项,第 3 项,第 4 项的二项式系数为C1 , C2 , C3 ,
依题意成等差数列,故2C2 C1 C3 ,得到: 2 n n 1 n n n 1 n 2 ,
n n n
2 1 3 2 1
化简得6 n 1 6 n 1 n 2 ,即: n2 9n 14 0 ,解得: n 7 或n 2 (舍去)故选:C
【一隅三反】
1.(2025·辽宁·一模)已知等差数列 an 的前n 项和为Sn ,若a3 a10 a6 4 ,则 S13 ( )
B.60 C.68 D.52
【答案】D
【解析】a a a a a 4 ,∴ a 4 ,∴ S
13 a1 a13 13a
52 ,故选:D.
3 10 6 7 6 7
13 2 7
2.(23-24 浙江)在V ABC 中,三个内角 A, B,C 成等差数列,则sin A C ( )
1
A. 2
【答案】C
B. 2
2
C. 3
2
D.1
【解析】因为 A, B,C 成等差数列,所以 A+C = 2B ;
又 A B C π ,所以3B π ,即 B π ,所以 A C 2B 2π ,所以sin A C sin 2 π 3 .故选:C.
3 3 3 2
3.(2025·广东汕头·模拟预测)已知a, b R , b 为a 和2 的等差中项,则3a 1 的最小值为( )
9b
1 1 2
A. 3 B. 2 C. 2 D. 3
【答案】D
【解析】由题知2b a 2 ,得到a 2b 2 ,所以3a 1
9b
32b 2 1
9b
9b 1 1
9b
1 9b 1 2
9 9b
2 ,
3
当且仅当 1 9b 1
9 9b
,即b 1 , a 1时,取等号.故选:D.
2
4(2025·安徽淮北·二模)若实数m 和n 的等差中项为 1,则m2 n2 的最小值为 .
【答案】2
【解析】若实数m 和n 的等差中项为 1,则m n 2 , m2 n2 2mn ,即2 m2 n2 m n 2 ,
m n 2 22
即m2 n2 2 ,当且仅当m n 1取等号.故
2 2
m2 n2 的最小值为 2.故答案为:2.
考向三 等差数列前 n 项和最值
【例 3-1】(2025·广西南宁·三模)设等差数列 an 的前 n 项和为 Sn ,若a5 2 , a3 a8 12 a7 ,则 Sn 的最小值为( )
14
【答案】C
49
4
12
10
【解析】假设等差数列 an 的公差为d ,由a3 a8 12 a7 得a3 a7 12 a8, 2a5 12 a5 3d 12 a5 3d,
所以3d 12 3a5 12 6 6 ,所以d 2 ,故an a5 (n 5)d 2n 8 ,
n a a n 6 2n 8
7 2 49
则S 1 n n n 7
n
则 Sn
S3 S4 12 .故选:C.
n 2 2
2 4
min
【例 3-2】(2025·江苏盐城·模拟预测)设等差数列 an 的前n 项和为 Sn ,若a1 0 , S9 S19 ,则当 Sn 取最小值时n 的值为( )
A.12 B.13 C.14 D.25
【答案】C
【解析】由S9 S19 可得a10 a11 a19 0 ,由等差数列的性质可得: 5(a14 a15 ) 0 ,因a1 0 ,则等差数列 an 的公差d 0 ,即等差数列 an 为递增数列,
故a14 0, a15 0 ,即 Sn 取最小值时, n 的值为 14.故选:C.
【例 3-3】(24-25 高三下·云南昭通·阶段练习)已知数列{an }是等差数列,其前 n 项和为 Sn ,若a3 a10 0 ,S11 0 ,则数列{Sn } 中最小的项是( )
S4
S5
S6
S7
【答案】C
【解析】因为 S
11(a1 a11 ) 11a
0 ,所以a 0 ,因为a a
a a
0 ,所以a 0 ,
11 2 6
6 6 7 3 10 7
所以公差d a7 a6 0 ,故当n 6 时, an 0 ,当n 7 时, an 0 ,所以当n 6 时, Sn 取得最小值,即{Sn } 中
最小的项是S6 ,故选:C.
【一隅三反】
1.(2025·江西·模拟预测)记 Sn 为等差数列 an 的前 n 项和,且a2 2a1 2 ,则满足 Sn 888的 n 的最大值为
( )
A.40 B.41 C.42 D.43
【答案】B
【解析】由已知可得a 1, a 2 , a 的公差为a a 1,故 a n ,故 S 1 2 3 n n(n 1) ,
2 n
1 n n 2
令 n(n 1) 888 ,又n N* ,所以n 41 ,故 n 的最大值为 41,
2
验证 S41
41 42 861 888 , S
2 42
42 43 903 888 ,所以 n 的最大值为 41.故选:B.
2
2.(24-25 陕西西安·期末)设等差数列 an 的前n 项和为Sn ,若a5 a8 0 , S11 0 ,则 Sn 的最大值为( )
A. S5
B. S6
C. S7
D. S8
【答案】B
【解析】因为数列 an 为等差数列,由a5 a8 0 a6 a7 0 ;
由S 0 11 a1 a11 0 a a 0 a 0 .所以a 0 .
11 1 11 6 7
所以等差数列 an 是首项为正数的递减数列,且前 6 项为正,从第 7 项开始为负数.所以 S6 最大.故选:B 3.(2025·山东泰安·模拟预测)公差不为0 的等差数列 an 的前n 项和为 Sn ,若a7 2 , a9 , a5 , a13 成等比数列,则满足Sn 0 的n 的最大值为( )
A. 8 B. 9 C.13 D.14
【答案】D
【解析】设数列 an 的公差为d ,
a1 6d 2
因为a 2 , a , a , a 成等比数列,所以
a1 20
, 解得 ,
7 9 5 13
a 8d a 12d a 4d 2
d 3
1 1 1
所以an
23 3n ,故 Sn
n 20 (23 3n) n(43 3n)
.
2 2
由S 0 ,得 n(43 3n) 0 ,解得0 n 43 . ∵ n N ,∴ n 的最大值为14 .故选:D.
n 2 3
4.(2025·甘肃金昌·模拟预测)()许多已知等差数列 an 的公差d 0 ,其前 n 项和记为 Sn , a1 0 ,则下列说法正确的是( )
A.数列 an 中有最大项 B.数列 Sn 中有最小项
C.若a a 0 ,则 55 S10 45
D.若 S
a , S
a ,则 S 取最小值时n 9
10 11 d
【答案】BC
20 20
21 21 n
【解析】对于 A,因为an a1 n 1 d ,且d 0 ,故 an 中无最大项,A 错误;
对于 B, a1 0 , d 0 ,故 m N* ,a 0 ,a 0 ,则Sm 为 Sn 中的最小项(当am 1 0 时, Sm , Sm 1 均
m 1
为 Sn 中的最小项),B 正确;
对于 C,若a a 0 ,则可知a 0, a 0 ,即a 9d 0 a 10d ,则可知 10 a1 9 ,故
10 11
10 11 1 1 d
S10 10a1 45d 10 a1 45 55, 45 ,C 正确;
d d d
对于 D,S20 a20 ,则可知 S19 0 ,则a10 0,又 S21 a21 ,则可知 S20 0 ,则a1 a20 0 ,即a10 a11 0 ,故a11 0 ,
故S10 最小,D 错误.故选:BC.
考向四 等差数列片段和的性质
【例 4-1】(24-25 广西)已知等差数列 an 的前n 项和为 Sn ,且 S4 2, S8 6 ,则 S12 ( )
A.8 B.10 C.12 D.16
【答案】C
【解析】因为 an 是等差数列,所以 S4 , S8 S4 , S12 S 8 也是等差数列,
所以2 S8 S4 S12 S8 S4 ,即2 6 2 S12 6 2 ,解得 S12 12 .故选:C.
【例 4-2】(24-25 河南)已知等比数列 an 的前 n 项和为 Sn ,若 S6 7, S12 21 ,则 S24 ( )
A.56 B.105 C.112 D.189
【答案】B
【解析】因为 S6 , S12 S6 , S18 S12 , S24 S18成等比数列,
即7,14, S 21, S S 成等比数列,所以142 7 S 21 ,解得 S 49 ,
18 24 18 18 18
又14 S S S 21 2 ,所以14 S 49 49 21 2 ,解得S 105 .
24 18 18 24 24
故选:B.
【例 4-3】(23-24 甘肃 )设等差数列 a 的前n 项和为 S ,若 S14 7 ,则 S21 ( )
18 3
n n
7
11
S14
11
A. 7 B. 2 C. 7 D. 6
【答案】A
【解析】在等差数列 an 中, S7 , S14 S7 , S21 S14 成等差数列,则2 S14 S7 S7 S21 S14 ,
设S m ,则 S 7m ,故2 7m m m S 7m ,解得 S 18m ,所以 S21 18m 18 .故选:A.
7 14
21 21
S14 7m 7
【例 4-4】(2024 高三·全国·专题练习)设等差数列 an 的前n 项和为Sn ,若 S12 288, S9 162 ,则S6 ( )
A.18 B.36 C.54 D.72
【答案】D
【解析】因为差数列 an 中, S3 , S6 S3 , S9 S6 , S12 S9 成等差数列,
即 x 54 y, x 198 3y ,解得S6 y 72 ,故选:D.
【一隅三反】
1.(24-25 江西)已知等差数列 an 的前n 项和为 Sn ,若 S3 12 , S6 S3 24 ,则 S12 S9 ( )
A.36 B.48 C.60 D.120
【答案】B
【解析】由等差数列片段和的性质, S3 , S6 S3 , S9 S6 , S12 S9 成等差数列,【公众号:林樾数学】故S9 S6 2( S6 S3) S3 36,则 S12 S9 2(S9 S6 ) (S6 S3 ) 48 .故选:B
2.(24-25 四川)已知Sn 是等差数列 an 的前 n 项和,若 S20 15 , S40 40 ,则 S60 ( )
A.75 B.65 C.50 D.55
【答案】A
【解析】由等差数列前n 项和的性质得: S20 , S40 S20 , S60 S40 成等差数列,
2 S40 S20 S20 S60 S40,即2 40 15 15 S60 40 ,解得 S60 75 .故选:A.
3.(2024·河南周口·模拟预测)设 Sn 为等差数列 an 的前 n 项和,已知 S3 4, S6 10 ,则a16 a17 a18 ( )
A.12 B.14 C.16 D.18
【答案】B
【解析】由等差数列的片段和性质知, S3, S6 S3, S9 S6 , S12 S9 , S15 S12 , S18 S15
成等差数列,
由S3 4, S6 S3 6 ,得该数列首项为 4,公差为 2,所以a16 a17 a18 S18 S15 4 5 2 14 .故选:B 4.(2025·吉林长春·二模)已知等差数列 an 的前 n 项和为 Sn ,若 S3 S9 6 ,则 S12 的值为( )
A.0 B.3 C.6 D.12
【答案】A
【解析】因为 an 是等差数列,所以 S3 , S6 S3 , S9 S6 , S12 S9 成等差数列,
又S3 S9 6 ,所以6, S6 6, 6 S6 , S12 6成等差数列,则6 S12 6 S6 6 6 S6 ,则 S12 0 .故选:A. 5.(2025·四川)设等差数列 an 的前n 项和 Sn ,若 S3 9 , S6 36 ,则a7 a8 a9 ( )
A.18 B.27 C.45 D.63
【答案】C
【解析】由题意得 S3 , S6 S3 , S9 S6 成等差数列,即9, 36 9, a7 a8 a9 成等差数列,
即2 36 9 9 a7 a8 a9 ,解得a7 a8 a9 45 .故选:C
6.(24-25 河南·阶段练习)已知等差数列{a }的前n 项和为S ,若 S3 3 ,则 S12 ( )
n n
6 9
3 3 5
A. 7 B.3 C. 2 D. 3
【答案】C
【解析】由题意设 S3 3t ,则 S6 7t ,由{an }是等差数列,所以 S3, S6 S3, S9 S6 , S12 S9 , 也成等差数列,
所以 S S 2 7t 3t 3t 5t ,解得 S 12t ;S S 2 12t 7t 4t 6t ,解得 S 18t ,所以 S12 18t 3 ,
9 6
故选:C.【公众号:林樾数学】
9 12 9 12
考向五 等差数列和与 n 的比值
S9 12t 2
【例 5-1】(2025·江西)已知数列 a 和 b 都是等差数列,且其前 n 项和分别为S 和T ,若 Sn 3n 1 ,则 a5
n n
( )
16 28 10
n n 2n 5 b
34
A. 15 B. 23 C. 11 D. 27
【答案】B
【解析】对于等差数列的前 n 项和满足 S 2n 1 a ,知道 an S2n 1 ,故 a5 S9 3 9 1 28 .故选:B.
2n 1
n b T
b T 2 9 5 23
n 2n 1 5 9
【例 5-2】(24-25 四川)已知等差数列 a , b 的前n 项和分别为 S ,T ,若 Sn 2n ,则 a2 a8 ( )
n n n n
T 3n 1
b b
20 5
n 3 7
10 9
A. 31 B. 8 C. 13 D. 14
【答案】D
【解析】因为等差数列 an , bn 的前 n 项和分别为 Sn , Tn ,
9(a1 a9 )
所以我们对 a2 a8 进行变形,得到 a2 a8 a1 a9 2 S9 ,
b3 b7
b3 b7
b1 b9
9(b1 b9 ) T9
2
因为 Sn 2n ,所以 S9 18 9 ,即 a2 a8 9 ,故 D 正确.
Tn
故选:D
3n 1
T9 28 14
b3 b7 14
【例 5-3】(2025·黑龙江哈尔滨·模拟预测)已知Sn , Tn 分别是等差数列 an , bn 的前 n 项和,且
Sn 2n 1 n N* ,则 a3 a8 ( )
Tn 4n 2
b4 b7
b5 b6
7 11 21 17
A. 10 B. 18 C. 38 D. 30
【答案】C
【解析】因为 an , bn 是等差数列,
所以 a3
a8
10 a1 a10
a3 a8 a1 a10 2 S10
,又 Sn 2n 1 n N ,
b4 b7
b5 b6
b5 b6
b1 b10
10 b1 b10
2
T10
Tn 4n 2
a3
所以
b4 b7
a8 b5 b6
S10
T10
2 10 1 21 ,
4 10 2 38
故选:C.
【例 5-4】(2025·湖北·模拟预测)已知等差数列 a , b 的前 n 项和分别为 S ,T ,若 Sn n ,则 a5 ( )
n n
5 9 9
n n 2n 1 b
3
A. 9 B. 17 C. 20 D. 5
【答案】D
【解析】因为等差数列 a , b 的前 n 项和分别为 S , T ,所以 a5 S5 S4 ,
n n n n
b T T
4 4 3
因为 Sn
n
,所以可设S
kn2 , T
kn 2n 1 ,则 S S
9k , T T
15k ,所以 a5 9k
3 .
Tn
故选:D.
2n 1 n n
5 4 4 3
b4 15k 5
【例 5-5】(23-24 湖北武汉)在等差数列 a 中, a 1,其前 n 项和为 S ,若 S8 S6 2 ,则 S 等于( )
n 1 n 8 6 10
A.10 B.100 C.110 D.120
【答案】B
【解析】因为数列 a 是等差数列,则数列 Sn 也为等差数列,设其公差为d ,
n
则 S8 S6 2 2d ,则d 1,又因为 S1 a 1 ,所以 Sn 1 n 1 n ,所以 S n2 ,所以 S 100 .
8 6
故选:B.
1 1 n
n 10
【例 5-6】(23-24 高三上·河南·阶段练习)已知等差数列 a 的前 n 项和为 S ,且 S7 S3 4 ,则a a ( )
n n 7 3 9 6
A. 2 B. 3 C. 4 D. 6
【答案】D
【解析】设等差数列 an 的公差为d ,
n 1 a n n 1 d na n n 1
则 S S
1 1
d n n 1 d ,
n 1 n 2 2 a d a d
n 1
n n 1
n 1 2
1 2 2
数列 Sn 是公差为 d 的等差数列, S7 S3 4 d 4 ,解得: d 2 , a a 3d 6 .故选:D.
7 3 2 9 6
【一隅三反】
1.(24-25 高三上·河南·期末)已知 S 与T 分别是等差数列 a 与等差数列 b 的前 n 项和,且 Sn 6n ,
则 a1
b6 b2020
a2025 b4 b2022
n n
( )
Tn n 2025
A.1 B.2 C.3 D.4
【答案】C
【解析】由等差数列的性质可知b6 b2020 b4 b2022 b1 b2025 ,
所以 a1 a2025 a1 a2025 S2025 6 2025 3. 故选:C
b6 b2020 b4 b2022 b1 b2025 T2025 2025 2025
2.(2024·河北衡水·三模)已知数列 an , bn 均为等差数列,其前n 项和分别为Sn,Tn ,满足(2n 3)Sn (3n 1)Tn,则 a7 a8 a9 ( )
b6 b10
A.2 B.3 C.5 D.6
【答案】A
【解析】因为数列 a , b 均为等差数列,可得a a a 3a 1 15a 1 S ,
n n 7 8 9 8 5
8 5 15
1 S
且b b b b ,又由T 15 b1 b15 ,可得b b 2 T .因此 a7 a8 a9 5 3 S15 3 4 2 .
6 10 1 15
15 2
6 10
15 15
b b
2 2 T 2 3
故选:A.
6 10
15 T15 15
3.(2025 湖北)已知 S ,T 分别是等差数列 a , b 的前项和,且 Sn 2n 1 (n N* ) ,则 a10 a11 ( )
n n n n
T 4n 2
b b b b
21 23
n
43 41
3 18 6 15
A. 38 B. 42 C. 82 D. 78
【答案】D
【解析】 S ,T 分别是等差数列 a , b 的前项和,故 an S2n 1 (n N* ) ,且b b
b b
b b ,故
n n n n b T
3 18 6 15 10 11
n 2n 1
a10 a11 a10 a11 a10 a11 S20 2 20 1 41 ,
b3 b18
故选:D
b6 b15
b10 b11
b10 b11
b10 b11
T20
4 20 2 78
4.(24-25 高三上·宁夏银川·阶段练习)已知等差数列 a 和 b 的前 n 项和分别为 S ,T ,若 Sn 3n 4 ,则
a3 a8 ( )
b2 b9
n n n n
Tn n 2
17 37 37 17
A. 13 B. 13 C. 6 D. 6
【答案】D
10 a1 a10
【解析】因为数列 a 和 b 均为等差数列,所以 a3 a8 a1 a10 2 S10
3 10 4 17 .
n n b b b b 10 b b T
10 2 6
故选:D.
2 9 1 10
1 10 10
2
5.(2025·江苏)已知两个等差数列 a 和 b 的前 n 项和分别为 Sn 和 Tn,且 Sn = 2n 70 ,则 a7 的值为( )
n n
48 42 84
Tn n 3 b6
1
A. 7 B.
【答案】A
5 C. 9 D. 4
【解析】因为 Sn = 2n 70 ,所以可设 S kn 2n 70 , T
kn n 3 , k 0 ,
Tn n 3
所以a S S
588k 492k 96k , b T T
54k 40k 14k ,所以 a7 96k 48 ,故选:A.
7 7 6
6 6 5
b6 14k 7
6.(23-24 河北保定·期末)已知数列 a 满足a a 6 , a 的前n 项和为S ,则 S2024 S2022
( )
n n 1 n n
n 2024 2022
A.12 B. 6 C. 3 D. 2
【答案】B
【解析】 an 1 an 6 , 数列 an 是以6 为公差的等差数列,
n 1 a n n 1 6
na n n 1 6
Sn 1 Sn
2 1 2
a
3n
a 3 n
1 3 ,
n 1
n n 1
n 1 1
数列 Sn 是以3 为公差的等差数列, S2024 S2022 2 3 6 .
故选:B.
2024 2022
7.(2025·贵州)等差数列 a 的前n 项和为S ,若 S2021 S2020 1 且a 3 ,则( )
n n 2021 2020 1
A. an 2n 1 B. an n 1
C. S 2n2 n D. S 4n2 n
【答案】A
【解析】设 a 的公差为 d,∵ S na n n 1 d ∴ Sn a n 1 d d n a d ,即{ Sn }为等差数列,公差
n n 1 2
n 1 2 2 1 2 n
为 d ,由 S2021 S2020
1知 d 1 d 2 ,故a
2n 1,S
n 3 2n 1 n 2 2n
﹒故选:A﹒
2 2021 2020 2
n n 2
8.(2024 高三·全国·专题练习)已知 Sn 是等差数列{an}的前 n 项和,若 a1=﹣2018, S2019 S2013
2019 2013
6 ,则 S2020
等于( )
A.﹣4040 B.﹣2020 C.2020 D.4040
【答案】C
【解析】∵Sn 是等差数列{an}的前 n 项和,∴数列{ Sn }是等差数列.
n
∵a1=﹣2018, S2019 S2013 6 ,∴数列{ Sn }的公差 d 6 1 ,首项为﹣2018,∴ S2020
2018+2019×1=1,
2019 2013 n 6
∴S2020=2020.故选:C.
2020
考向六 等差数列的奇数项(偶数项)之和
【例 6-1】(2025 河南)一个等差数列共 100 项,其和为 80,奇数项和为 30,则该数列的公差为( )
1 1 2
A. 4 B.2 C. 3 D. 5
【答案】D
【解析】设等差数列的公差为d ,则由条件可知:数列的奇数项之和为a1 a3 a5 a99 30 ,①
偶数项之和为a2 a4 a6 a100 80 30 50 ,②
由②-①,得50d 20 ,所以d 2 ,即该数列的公差为 2 .
5 5
故选:D.
【例 6-2】(2025 陕西)等差数列 an
共 2n+1 个项,且奇数项和为 165,偶数项和为 150,则 n=( )
A.10 B.13 C.11 D.22
【答案】A
【解析】等差数列 an
共 2n+1 个项,其中奇数项有n 1个,偶数项有n 个,
设等差数列 a 的公差为d ,奇数项和a a
a
n 1 a n 1 n 2d
n 1 a nd 165 ①,
n 1 3 2 n 1 1 2 1
偶数项和a a
a
n a d n n 1 2d
n a nd 150 ②,
2 4 2 n 1 2 1
①-②得a1 nd 15 ,则n 15 150, n 10 .故选:A
【一隅三反】
1.(2023·重庆·二模)已知等差数列 an 的前 30 项中奇数项的和为A ,偶数项的和为 B ,且 B A 45 ,
2 A B 615 ,则an ( )
3n 2
3n 1
3n 1
3n 2
【答案】B
【解析】设等差数列的公差为d ,首项为a1 ,则 B A 15d 45 ,所以d 3,
因为2 A B 615 ,即2A A 45 615 ,则 A 660 ,
等差数列的奇数项是以a1 为首项, 2d 为公差的等差数列,等差数列 an 的前 30 项中奇数项有 15 项,所以
A 15a 15 14 6 660,得a 2 ,
1 2 1
所以an a1 n 1 d 2 3 n 1 3n 1.
故选:B
2.(2025 河南)已知等差数列 a 的公差d 1 , a a a
80 ,那么 S ( )
n 2 2 4 100
100
A.80 B.120 C.135 D.160
【答案】C
【解析】在等差数列 a 中,公差d 1 , a a a
80 ,
n 2 2 4 100
所以a a a a a
a 50d 80 50 1 55 ,
1 3 99 2 4
100 2
所以 S100 a1 a3 a99 a2 a4 a100 80 55 135 ,故选:C
3.(2025 上海)设等差数列的项数n 为奇数,则其奇数项之和与偶数项之和的比为( )
n 1
n
2n 1
n
2n 1
2n
n 1
n 1
【答案】D
【解析】由题知,奇数项有
n 1 2
项,偶数项有
n 1
项,
2
奇数项之和为 n 1 a
n 1 n 1
2 2
2 d n 1
n 1 d),
2 1 2 2
n 1 n 3
( a1 2
偶数项之和为 n 1 (a d ) 2 2
2d n 1 (a n 1 d ,
2 1 2 2 1 2
n 1
所以奇数项之和与偶数项之和的比为
故选:D
n 1 ,
考向七 等差数列的证明与判断
【例 6-1】(2025·全国一卷·高考真题)设数列 a 满足a 3 , an 1 an 1
,证明: na 为等差数列;
【答案】证明见解析
【解析】由题意证明如下, n N* ,
n 1 n n 1
n(n 1) n
在数列 a 中, a 3 , an 1 an
1 ,∴ n 1 a
na
1,即 n 1 a
na
1,
n 1 n n 1
n n 1
n 1 n
n 1 n
∴ nan 是以a1 3 为首项,1 为公差的等差数列.
【例 6-2】(2025·福建厦门·三模)已知数列 a 的前项和为 S ,a 1,且na S n2 n ,证明:数列 Sn
为等差数列;
n n 1
n 1 n
【答案】证明见解析;
【解析】由 S1 a1 1 , na
n(S
S ) S
n2 n ,则nS
(n 1) S
n(n 1),
1 1 n 1
n 1 n n
n 1 n
所以 Sn 1 Sn 1 ,故 Sn 是首项、公差均为 1 的等差数列;
n 1 n
【一隅三反】
1.(2025·江西新余·模拟预测)已知数列 a 的前n 项和为S , a
3S S
0 , a 1 .
1
n n n 1
n n 1 1 3
证明:数列
为等差数列;
n
求 an 的通项;
1
求 a 的最大值.
n
【答案】(1)证明见解析;
1 , n 1
3
an
1
3n n 1
;
, n 2
3.
【解析】(1)因为a
S S
,所以 S S
3S S ,故 1
1 3 ,
n 1
n 1 n
n n 1
n 1 n
Sn 1 Sn
又 1 1 3 ,所以 1 是以 3 为首项,3 为公差的等差数列.
S1 a1
n
1
(2)由(1)知
n
3 n 1 3 3n Sn
3n ,
当n 2 时, a
3 1 1
1 ,
n 3n 3n 3
3n n 1
而n 1 时, a 1 不满足题意,
n 3
1 , n 1
3
所以an
1
3n n 1
.
, n 2
1
(3)由(2)知,当n 2 时,
n
3n n 1 0 ,
又 1 3 0 ,所以, 1 的最大值为 1 3.
a a a
1 n 1
2.(24-25 高三下·甘肃庆阳·期中)记 Sn 为正项数列 an 的前n 项和,且a1Sn n 1 an .
(1)求a1 的值;
(2)判断 an 是否为等差数列,并求 a 的通项公式;
【答案】(1) a1 2
(2) an 是常数列,也是等差数列, a
n
n
2n .
【解析】(1)令 n 1 可得a2 2a , 又a 0 ,故a 2 .
1 1 1 1
(2) 2Sn n 1 an ,① 2Sn 1 n 2 an 1 ,②
由②-①,得2a n 2 a n 1 a ,即na n 1 a 故 an 1 an ,故 an 是常数列,也是等差数列
n 1
故 an a1 2 ,故a
2n .
n 1
n n 1
n n 1 n
n 1 n
3.(2025·河南许昌·三模)在数列 an 中, a1 0, a2 4 ,且an 2 2an 1 an 2 ,证明: an 1 an 是等差数列;
【答案】证明见解析
【解析】 在数列 an 中, a1 0, a2 4 ,且an 2 2an 1 an 2 ,
a 2 an 1 an 1 an 2a 1 a 2 an 1 a 1 an 2 ,
an 1 an 是首项为a2 a1 4 ,公差为 2 的等差数列.
4.(2025·甘肃白银·模拟预测)已知数列 a 满足a 2 , a
an ,
n为奇数,数列 b 满足b a .
n 1 n 1
a 1, n为偶数
n n 2n 1
n
(1)证明:数列 bn 为等差数列;
(2)求数列 bn 的通项公式及前 n 项和 Sn ;
【答案】(1)证明见解析
(2) bn
n 1
, Sn
n2 3n 2
【解析】(1) bn 1 bn a2n 1 a2n 1 a2n 1 a2n 1 1 ,
所以数列 bn 为等差数列,首项为b1 a1 2 ,公差为 1.
(2) bn
2 n 1 1 n 1
, Sn
2 n 1 n n2 3n
2 2
考向八 含绝对值的等差数列的前 n 项和
【例 7-1】(23-24 高三上·贵州·阶段练习)记等差数列 an 的前n 项和为Sn ,已知a1 11, S3 S9 .
(1)求 an 的通项公式;
(2)记数列 an 的前n 项和为Tn ,求T100 .
【答案】(1) an 2n 13 (2)8872
【解析】(1)由 S3 S9 a4 a5 a6 a7 a8 a9
0 a6 a7
0 则a12 a1 11
设 an 的公差为d 则a1 11d 11 11 11d 11 d 2 则an a1 n 1 d 11 2 n 1 2n 13
所以数列 an 的通项公式为an 2n 13 .
(2)由题可知T100 a1 a2 a6 a7 a100 T100 a1 a2 a6 a7 a100
T S
S
S 2S S
2 6 11 1 100 11 187 8872 , T
8872 .
100 6 100 6 6 100 2 2
100
【例 7-2】(24-25 高三上·湖北·开学考试)已知数列 an 的前n 项和为 Sn ,且a1 2, an 1 Sn 2 .
(1)求数列 an 的通项公式;
(2)设b
log a2 11,求数列 b 的前n 项和T .
【答案】(1) a 2n , n N*
10n n2 , n 5
(2) Tn n2 10n 50, n 6
, n N* .
【解析】(1)由 an 1 Sn 2 ,则当n 2 时an Sn 1 2
两式相减得an 1 an an ,所以an 1 2an n 2 .将a1 2 代入an 1 Sn 2 得, a2 4 2a1,所以对于n N*, a 2a ,故 a 是首项为 2,公比为 2 的等比数列,所以a 2n .
(2) b log a 2 11 2n 11 . B b b b
n n 10 n2 10n ,
n 2 n n 1 2 n
因为当n 5 时b 0 ,当n 6 时b 0 ,所以当 n 5时, T b b b B
10n n 2 ,
n n n 1 2 n n
当n 6 时, T
b b
b b b
b
B 2B
n 2 10n 50 .故T
10n n2 , n 5
.
n
【一隅三反】
1 2 5 6 7
n n 5
n n2 10n 50, n 6
1.(2024·全国·模拟预测)已知等差数列 an , a1 10 ,记 Sn 为 an 的前n 项和,从下面①②③中再选取一
个作为条件,解决下面问题.① 2a a 0;② S 55 ;③ S7 S5 2 .
5 8 11 7 5
(1)求Sn 的最小值;
(2)设 an 的前n 项和为Tn ,求T20 .
【答案】(1)答案见解析
(2)答案见解析
【解析】(1)设等差数列 an 的公差为d ,且a1 10 .
选择①:(1)因为2a5 a8 0,所以3a1 15d 0 ,解得d 2 .
所以a a (n 1)d 2n 12 ,则 S na n(n 1) d n2 11 n,
n 1 n 1 2
利用二次函数对称性和开口方向知, S n2 11n 关于 n 5.5 对称,
因为n N* ,所以当n 5 或 6 时, Sn S5 S 6 30 .
选择②:因为S 55 ,可得11 (a1 a11) 55 ,
11 2
因为a 10 ,所以a 0 ,此时d a11 a1 1 ,所以a a (n 1)d n 11 ,
1 11
11 1 n 1
因为d 0 ,所以 an 单调递增,且当n 11时, an 0 .
所以当n 10 或 11 时, Sn 最小,此时 Sn S10 S11 55 .
选择③:因为 S7 S5 2 ,所以 a1 a7 a1 a5 2 ,即a a 4 ,所以d a7 a5 2 ,
7 5 2 2 7 5 2
所以a a (n 1)d 2n 12 ,则 S na n(n 1) d n2 11 n,
n 1 n 1 2
利用二次函数对称性和开口方向知, S n2 11n 关于 n 5.5 对称,【公众号:林樾数学】因为n N* ,所以当n 5 或 6 时, Sn S5 S 6 30 .
(2)解:若选择①或③:由(1)知an 2n 12 ,当n 6 时, an 0 ,
所以T20 a1 a2 a3 a20 a1 a2 a3 a3 a5 a6 a7 a20
T20 a1 a2 a3 a20 2( a1 a2 a3 a3 a5) S20 2S5 240 .
若选择②:由(1)知an
n 11,且当n 11时, an 0 ,且 Sn
1 n 2 21 n ,
2 2
所以T20 a1 a2 a3 a20 a1 a2 a10 a11 a12 a20
T20 a1 a2 a3 a20 2( a1 a2 a3 a10) S20 2S10 100 .
2(2023·全国乙卷·高考真题)记 Sn 为等差数列 an 的前n 项和,已知a2 11, S10 40 .
(1)求 an 的通项公式;
(2)求数列 an 的前n 项和Tn .
【答案】(1) an 15 2n
14n n2 , n 7
(2) Tn n2 14n 98, n 8
【解析】(1)设等差数列的公差为 d ,
a2 a1 d 11
a1 d 11
a1
13
由题意可得 S 10a 10 9 d 40 ,即 2a 9d 8 ,解得 d 2 ,
10 1 2 1
所以an 13 2 n 1 15 2n ,
n 13 15 2n 2
(2)因为 Sn
14n n ,
2
令an
15 2n 0 ,解得n 15 ,且n N* ,
2
当n 7 时,则a 0 ,可得T a a a a a a S 14n n2 ;
n n 1 2 n 1 2 n n
当n 8 时,则an 0 ,可得Tn a1 a2 an a1 a2 a7 a8 an
S S S 2S S 2 14 7 7 2 14n n 2 n 2 14n 98 ;【公众号:林樾数学】
14n n2 , n 7
综上所述: Tn n2 14n 98, n 8 .
考向九 等差数列的简单应用
【例 8-1】(23-24 高三下·重庆渝中·阶段练习)中国载人航天工程发射的第十八艘飞船,简称“神十八”,于 2024年 4 月执行载人航天飞行任务.运送“神十八”的长征二号F运载火箭,在点火第一秒钟通过的路程为2km ,以后每秒钟通过的路程都增加3km ,在达到离地面222km的高度时,火箭开始进入转弯程序.则从点火到进入转弯程序大约需要的时间是( )秒.
A.10 B.11 C.12 D.13
【答案】C
【解析】设出每一秒钟的路程为数列{an },由题意可知{an }为等差数列,
则数列首项a1 2 ,公差d 3,所以an a1 n 1 d 2 n 1 3 3n 1,
由求和公式有 Sn
n a1 an (3n 1 2)n 222 ,解得n 12 ,故选:C.
2 2
【例 8-2】(24-25 山东 )“中国剩余定理”又称“孙子定理”,原文如下:今有物不知其数,三三数之剩二(除以 3
余 2),五五数之剩三(除以 5 余 3),七七数之剩二(除以 7 余 2),问物几何?现有这样一个相关的问题:已知正整数 p( p 1) 满足二二数之剩一,三三数之剩一,将符合条件的所有正整数 p 按照从小到大的顺序排成一列,构
成数列 a ,记数列 a 的前 n 项和为 S ,则 2Sn an 23 的最小值为( )
n n n n
A.26 B.36 C.38 D.46
【答案】C
【解析】二二数之剩一、三三数之剩一的数分别为2m 1、3k 1, m,k N ,
因此数列{an }的项即为以上两类数的公共项6n 1,即an 6n 1, n N ,而an 1 an (6 n 7) (6 n 1) 6,则数列{an }是等差数列,
n(7 6n 1) 2
2S a 23 6n2 14n 24 4
于是 Sn 2 3n
4n , n n 6(n
n n n
) 14 ,
又对勾函数 y x 4 在(0, 2] 上单调递减,在[2, ) 上单调递增,
x
所以n 2 时, 2Sn an 23 取得最小值 38.故选:C
n
【一隅三反】
1.(2024·广东广州·模拟预测)元代数学家朱世杰编著的《算法启蒙》中记载了有关数列的计算问题:“今有竹七节,下两节容米四升,上两节容米二升,各节欲均容,问逐节各容几升?”其大意为:现有一根七节的竹子,最下面两节可装米四升,最上面两节可装米二升,如果竹子装米量逐节等量减少,问竹子各节各装米多少升?以此计算,这根竹子的装米量为( )
A. 9 升 B.10.5 升 C.12 升 D.13.5 升
【答案】B
【解析】依题意,竹子自下而上的各节装米量构成等差数列{a }, n N , n 7 ,则a1 a2 4, a6 a7 2 , a1 a7 a2 a6 3 ,
所以这根竹子的装米量为S7
故选:B
7(a1 a7 ) 10.5 (升).【公众号:林樾数学】
2
2.(2025 江西抚州·期中)我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度),二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是( )
A.相邻两个节气晷长减少或增加的量为十寸 B.秋分的晷长为 75 寸
C.立秋的晷长比立春的晷长长 D.立冬的晷长为一丈五寸
【答案】C
【解析】由题意可知夏至到冬至的晷长构成等差数列 an ,其中a1 15 寸, a13 135 寸,公差为d 寸,则
135 15 12d ,解得d 10 (寸),
同理可知由冬至到夏至的晷长构成等差数列 bn ,首项b1 135 ,末项b13 15 ,公差d 10 (单位都为寸).故选项 A 正确;
春分的晷长为b7 , b7 b1 6d 135 60 75,
秋分的晷长为a7 , a7 a1 6d 15 60 75,所以B 正确;
立冬的晷长为a10 , a10 a1 9d 15 90 105 ,即立冬的晷长为一丈五寸, D 正确;
立春的晷长,立秋的晷长分别为b4 , a4 ,【公众号:林樾数学】
a4 a1 3d 15 30 45, b4 b1 3d 135 30 105, b4 a4 ,故错C 误.故选:C.
3.(2023·四川达州·一模)《孙子算经》是我国南北朝时著名的数学著作,其中有物不知数问题:今有物不知
其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?意思是:有一些物品,不知道有多少个,只知道将它们三个三个地数,会剩下 2 个;五个五个地数,会剩下 3 个;七个七个地数,也会剩下 2 个.这些物品
的数量是多少个?若一个正整数除以三余二,除以五余三,将这样的正整数由小到大排列,则前 5 个数的和为
( )
A.189 B.190 C.191 D.192
【答案】B
【解析】根据题意,被以 3 除余 2,除以 5 余 3 的数,构成首项为8 ,公差为15 的等差数列,
则an 8 (n 1) 15 15n 7,
所以将这样的正整数由小到大排列,则前 5 个数的和为故选:B.
5 8 15 5 7
2
190 .
同课章节目录
