苏科版2024—2025学年七年级下学期数学期末质量检测卷(含答案)
文档属性
| 名称 | 苏科版2024—2025学年七年级下学期数学期末质量检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 654.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
苏科版2024—2025学年七年级下学期数学期末质量检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.某校近期开展了“探索纹样世界,走近东方图腾”主题活动,以下图案是同学们设计的图腾纹样作品,其中文字上方的图案是轴对称图形的是( )
A. B. C. D.
2.下列命题中,是真命题的是( )
A.相等的角是对顶角 B.邻补角的平分线相互垂直
C.互补的两个角一定是一个锐角,另一个为钝角 D.同位角相等
3.若,则下列不等式成立的是( )
A. B.
C. D.
4.若关于的方程组的解满足,则的取值范围是( )
A. B. C. D.
5.若关于x,y的二元一次方程的一个解,则m的值为( )
A. B. C. D.3
6.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A.B.C.D.
7.若关于x,y的二元一次方程组的解为,则关于x,y的方程组的解为( )
A. B. C. D.
8.计算的结果为( )
A. B. C.1 D.
9.已知a、b均为常数,若的乘积不含x的一次项,则a与b的数量关系为( )
A. B. C. D.
10.如图1,现有边长为和的正方形纸片各一张,长和宽分别为,的长方形纸片一张.把纸片Ⅰ,Ⅱ按图2所示的方式放入纸片Ⅱ内,若图2中阴影部分的面积和满足,则,满足的关系式为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.已知式子(2x+3)(x﹣a)的计算结果中不含x的一次项,则a的值为 .
12.目前世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为 .
13.已知a2+ab+b2=6,a2﹣ab+b2=10,则a+b= .
14.如图,在△ABC中,∠B=90°,AB=6,将△ABC沿着BC的方向平移至△DEF,若四边形ADFC的面积为24,则平移的距离为 .
15.结合“(a b)n=anbn(n是正整数),即积的乘方等于乘方的积”计算22025= .
16.已知有甲、乙两个长方形,它们的边长如图所示(m为正整数),甲、乙的面积分别为S1,S2.若满足条件|S1﹣S2|<n≤2023的整数n有且只有4个,则m的值为 .
第II卷
苏科版2024—2025学年七年级下学期数学期末质量检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明
17.计算:
(1) (2)
18.先化简,再求值:,其中满足.
19.解方程组:
(1) (2)
20.解不等式组:
(1) (2)解不等式组,并写出它的整数解
21.我省的冰雪旅游已进入爆发式增长,某旅游商品经销店欲购进A,B两种冰雪纪念品,若用380元可以购进A 种纪念品7件,B种纪念品8件;也可以用380元购进A种纪念品10件, B种纪念品6件.
(1)求A,B两种纪念品的进价分别为多少元;
(2)若该经销店每件A 种纪念品售价25元,每件B种纪念品售价39元,该经销店准备购进A,B两种纪念品共40件, 且这两种纪念品全部售出后总获利不低于300元,该经销店最多可购进A 种纪念品多少件.
22.已知关于,的方程组和有相同的解.
(1)求,的值;
(2)证明:无论取何值,方程组的解都是关于,的方程的解.
23.如果,那么我们规定.
如:因为,所以.
(1)【理解】根据上述规定,填空:___________,___________;
(2)【说理】记.试说明:;
(3)【应用】若,直接写出的值.
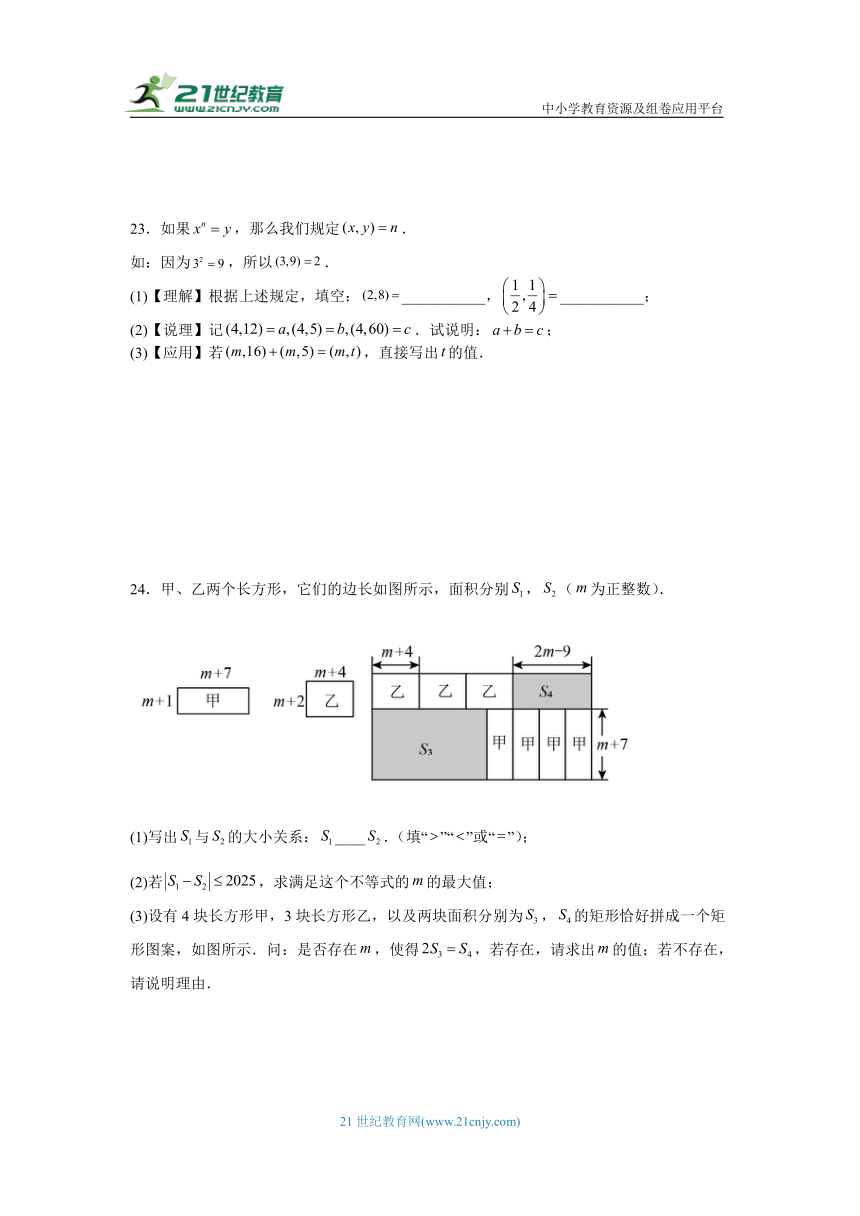
24.甲、乙两个长方形,它们的边长如图所示,面积分别,(为正整数).
(1)写出与的大小关系:____.(填“”“”或“”);
(2)若,求满足这个不等式的的最大值;
(3)设有4块长方形甲,3块长方形乙,以及两块面积分别为,的矩形恰好拼成一个矩形图案,如图所示.问:是否存在,使得,若存在,请求出的值;若不存在,请说明理由.
25.我们把关于x,y的二元一次方程,叫作数对的“伴随方程”;若是关于x,y的二元一次方程的一个解,则称数对是数对的“伴随数对”.
(1)已知数对,在数对中,是数对的“伴随数对”的是 ;
(2)若数对是数对和数对的“伴随数对”,求数对的“伴随方程”;
(3)若是n个不同的数对,满足前一个数对是后面所有数对的“伴随数对”,且n的最大值是t,如果关于x的不等式组恰好有2024个整数解,直接写出m的取值范围.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D C D A D C A C
二、填空题
11.【解答】解:∵多项式(2x+3)(x﹣a)=2x2+(3﹣2a)x﹣3a不含x的一次项,
∴3﹣2a=0,
解得a.
故答案为:.
12.【解答】解:0.000000076=7.6×10﹣8.
故答案为:7.6×10﹣8.
13.【解答】解:两式相减,得2ab=﹣4,
解得ab=﹣2,
∴(a+b)2=a2+2ab+b2=6+ab=6﹣2=4,
∴a+b=2或﹣2.
故答案为:2或﹣2.
14.【解答】解:由平移得:AD∥CF,AD=CF,
∴四边形ADFC是平行四边形,
∵四边形ADFC的面积为24,∠B=90°,
∴CF AB=24,
∵AB=6,
∴CF=4,
∴平移的距离为4,
故答案为:4.
15.【解答】解:22025
=()202322025
=()2023×(2)×22024
=(2)2023×3×2
=6.
故答案为:6.
16.【解答】解:∵,
,
∴S1﹣S2=2m﹣1,
∵满足条件|S1﹣S2|<n≤2023的整数n有且只有4个,
∴n可取正整数为2023,2022,2021,2020,
∴2019≤|S1﹣S2|<2020,
即2019≤|2m﹣1|<2020,
∵m为正整数,
∴2m﹣1>0
∴2019≤2m﹣1<2020,
解得:1010≤m<1010.5,
∴m=1010,
故答案为:1010.
三、解答题
17.【解】(1)解:原式
;
(2)解:原式
.
18.【解】解:
,
∵,
∴,,
∴,,
∴原式.
19.【解】(1)解:,
得:,
解得:,
将代入①得:,
解得:,
故原方程组的解为;
(2)解:
原方程组整理得,
得:,
解得:,
将代入①得:,
解得:,
故原方程组的解为.
20.【解】(1)解:
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:;
(2)解:
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:,
∴整数解为:,,.
21.【解】(1)解:设A、B两种纪念品的进价分别为x元、y元.
由题意得 ,
解得
答:A、B两种纪念品的进价分别为20 元、30元.
(2)解;设该经销店购进A种纪念品a件, 则购进B种纪念品件,
由题意,得,
解得,
答:该经销店最多可购进A种纪念品15件.
22.【解】(1)解:由题意可得:,
解得;
将代入含有m、n的方程得:,
解得:;
(2)证明:当时,方程的左边
,
∴无论取何值,方程组的解都是关于,的方程的解.
23.【解】(1)解:∵ ,
∴,
∵,
∴,
故答案为:;;
(2)证明:∵,
∴,
∴,
∴,
∴;
(3)解:设,
∴,,,
∵,
∴,
∴,
∴,
即,
∴.
24.【解】(1)解:,
,
,
是正整数,
,
,
,
,
故答案为:;
(2)解:,,
,
,
解得:,
的最大值为;
(3)解:不存在,
理由如下:
如下图所示,
,
,
,
,
整理得:,
解得:
为正整数,
不存在使得.
25.【解】(1)解:由题意得:“伴随方程”为:
将点代入得,
将点代入得,
将点代入得,
将点代入得,
∴点,是数对的“伴随数对”,
故答案为:;
(2)解:由题意得,,
解得:,
∴数对的“伴随方程”为:;
(3)解:∵两个二元一次方程可得唯一解,
∴当,确定时,即可确定,
∴,
∴不等式组为,
∴解得
∵关于x的不等式组恰好有2024个整数解,
∴这2024个整数解为,
∴,
解得:.
21世纪教育网(www.21cnjy.com)
苏科版2024—2025学年七年级下学期数学期末质量检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.某校近期开展了“探索纹样世界,走近东方图腾”主题活动,以下图案是同学们设计的图腾纹样作品,其中文字上方的图案是轴对称图形的是( )
A. B. C. D.
2.下列命题中,是真命题的是( )
A.相等的角是对顶角 B.邻补角的平分线相互垂直
C.互补的两个角一定是一个锐角,另一个为钝角 D.同位角相等
3.若,则下列不等式成立的是( )
A. B.
C. D.
4.若关于的方程组的解满足,则的取值范围是( )
A. B. C. D.
5.若关于x,y的二元一次方程的一个解,则m的值为( )
A. B. C. D.3
6.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A.B.C.D.
7.若关于x,y的二元一次方程组的解为,则关于x,y的方程组的解为( )
A. B. C. D.
8.计算的结果为( )
A. B. C.1 D.
9.已知a、b均为常数,若的乘积不含x的一次项,则a与b的数量关系为( )
A. B. C. D.
10.如图1,现有边长为和的正方形纸片各一张,长和宽分别为,的长方形纸片一张.把纸片Ⅰ,Ⅱ按图2所示的方式放入纸片Ⅱ内,若图2中阴影部分的面积和满足,则,满足的关系式为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.已知式子(2x+3)(x﹣a)的计算结果中不含x的一次项,则a的值为 .
12.目前世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为 .
13.已知a2+ab+b2=6,a2﹣ab+b2=10,则a+b= .
14.如图,在△ABC中,∠B=90°,AB=6,将△ABC沿着BC的方向平移至△DEF,若四边形ADFC的面积为24,则平移的距离为 .
15.结合“(a b)n=anbn(n是正整数),即积的乘方等于乘方的积”计算22025= .
16.已知有甲、乙两个长方形,它们的边长如图所示(m为正整数),甲、乙的面积分别为S1,S2.若满足条件|S1﹣S2|<n≤2023的整数n有且只有4个,则m的值为 .
第II卷
苏科版2024—2025学年七年级下学期数学期末质量检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明
17.计算:
(1) (2)
18.先化简,再求值:,其中满足.
19.解方程组:
(1) (2)
20.解不等式组:
(1) (2)解不等式组,并写出它的整数解
21.我省的冰雪旅游已进入爆发式增长,某旅游商品经销店欲购进A,B两种冰雪纪念品,若用380元可以购进A 种纪念品7件,B种纪念品8件;也可以用380元购进A种纪念品10件, B种纪念品6件.
(1)求A,B两种纪念品的进价分别为多少元;
(2)若该经销店每件A 种纪念品售价25元,每件B种纪念品售价39元,该经销店准备购进A,B两种纪念品共40件, 且这两种纪念品全部售出后总获利不低于300元,该经销店最多可购进A 种纪念品多少件.
22.已知关于,的方程组和有相同的解.
(1)求,的值;
(2)证明:无论取何值,方程组的解都是关于,的方程的解.
23.如果,那么我们规定.
如:因为,所以.
(1)【理解】根据上述规定,填空:___________,___________;
(2)【说理】记.试说明:;
(3)【应用】若,直接写出的值.
24.甲、乙两个长方形,它们的边长如图所示,面积分别,(为正整数).
(1)写出与的大小关系:____.(填“”“”或“”);
(2)若,求满足这个不等式的的最大值;
(3)设有4块长方形甲,3块长方形乙,以及两块面积分别为,的矩形恰好拼成一个矩形图案,如图所示.问:是否存在,使得,若存在,请求出的值;若不存在,请说明理由.
25.我们把关于x,y的二元一次方程,叫作数对的“伴随方程”;若是关于x,y的二元一次方程的一个解,则称数对是数对的“伴随数对”.
(1)已知数对,在数对中,是数对的“伴随数对”的是 ;
(2)若数对是数对和数对的“伴随数对”,求数对的“伴随方程”;
(3)若是n个不同的数对,满足前一个数对是后面所有数对的“伴随数对”,且n的最大值是t,如果关于x的不等式组恰好有2024个整数解,直接写出m的取值范围.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D C D A D C A C
二、填空题
11.【解答】解:∵多项式(2x+3)(x﹣a)=2x2+(3﹣2a)x﹣3a不含x的一次项,
∴3﹣2a=0,
解得a.
故答案为:.
12.【解答】解:0.000000076=7.6×10﹣8.
故答案为:7.6×10﹣8.
13.【解答】解:两式相减,得2ab=﹣4,
解得ab=﹣2,
∴(a+b)2=a2+2ab+b2=6+ab=6﹣2=4,
∴a+b=2或﹣2.
故答案为:2或﹣2.
14.【解答】解:由平移得:AD∥CF,AD=CF,
∴四边形ADFC是平行四边形,
∵四边形ADFC的面积为24,∠B=90°,
∴CF AB=24,
∵AB=6,
∴CF=4,
∴平移的距离为4,
故答案为:4.
15.【解答】解:22025
=()202322025
=()2023×(2)×22024
=(2)2023×3×2
=6.
故答案为:6.
16.【解答】解:∵,
,
∴S1﹣S2=2m﹣1,
∵满足条件|S1﹣S2|<n≤2023的整数n有且只有4个,
∴n可取正整数为2023,2022,2021,2020,
∴2019≤|S1﹣S2|<2020,
即2019≤|2m﹣1|<2020,
∵m为正整数,
∴2m﹣1>0
∴2019≤2m﹣1<2020,
解得:1010≤m<1010.5,
∴m=1010,
故答案为:1010.
三、解答题
17.【解】(1)解:原式
;
(2)解:原式
.
18.【解】解:
,
∵,
∴,,
∴,,
∴原式.
19.【解】(1)解:,
得:,
解得:,
将代入①得:,
解得:,
故原方程组的解为;
(2)解:
原方程组整理得,
得:,
解得:,
将代入①得:,
解得:,
故原方程组的解为.
20.【解】(1)解:
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:;
(2)解:
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:,
∴整数解为:,,.
21.【解】(1)解:设A、B两种纪念品的进价分别为x元、y元.
由题意得 ,
解得
答:A、B两种纪念品的进价分别为20 元、30元.
(2)解;设该经销店购进A种纪念品a件, 则购进B种纪念品件,
由题意,得,
解得,
答:该经销店最多可购进A种纪念品15件.
22.【解】(1)解:由题意可得:,
解得;
将代入含有m、n的方程得:,
解得:;
(2)证明:当时,方程的左边
,
∴无论取何值,方程组的解都是关于,的方程的解.
23.【解】(1)解:∵ ,
∴,
∵,
∴,
故答案为:;;
(2)证明:∵,
∴,
∴,
∴,
∴;
(3)解:设,
∴,,,
∵,
∴,
∴,
∴,
即,
∴.
24.【解】(1)解:,
,
,
是正整数,
,
,
,
,
故答案为:;
(2)解:,,
,
,
解得:,
的最大值为;
(3)解:不存在,
理由如下:
如下图所示,
,
,
,
,
整理得:,
解得:
为正整数,
不存在使得.
25.【解】(1)解:由题意得:“伴随方程”为:
将点代入得,
将点代入得,
将点代入得,
将点代入得,
∴点,是数对的“伴随数对”,
故答案为:;
(2)解:由题意得,,
解得:,
∴数对的“伴随方程”为:;
(3)解:∵两个二元一次方程可得唯一解,
∴当,确定时,即可确定,
∴,
∴不等式组为,
∴解得
∵关于x的不等式组恰好有2024个整数解,
∴这2024个整数解为,
∴,
解得:.
21世纪教育网(www.21cnjy.com)
同课章节目录
