北师大版六年级上册数学圆的面积(一)课件(共23张PPT)
文档属性
| 名称 | 北师大版六年级上册数学圆的面积(一)课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 26.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
圆的面积(一)
回忆一下,平行四边形的面积公式是怎样推导出来的
原来平行四边形的底
(长方形的长)
平行四边形等图形的面积计算公式是怎样推导得出的?
h
a
h
a
都用了“转化”的方法。
h
a
h
a
我们学过哪些图形的面积呢 是怎样推导的?
平行四边形的面积=底×高
三角形的面积=底×高÷2
梯形的面积=(上底+下底)×高÷2
转化
什么是面积呢?
面积就是图形所占平面的大小。
圆的面积就是圆所占平面的大小。
探究体验,经历过程
能否将圆转化成以前学过的图形呢?
长方形、平行四边形、梯形的面积公式是怎么推导的呢?
数格子
割补法
拼凑法
转化思想
如何得到一个圆的面积呢?
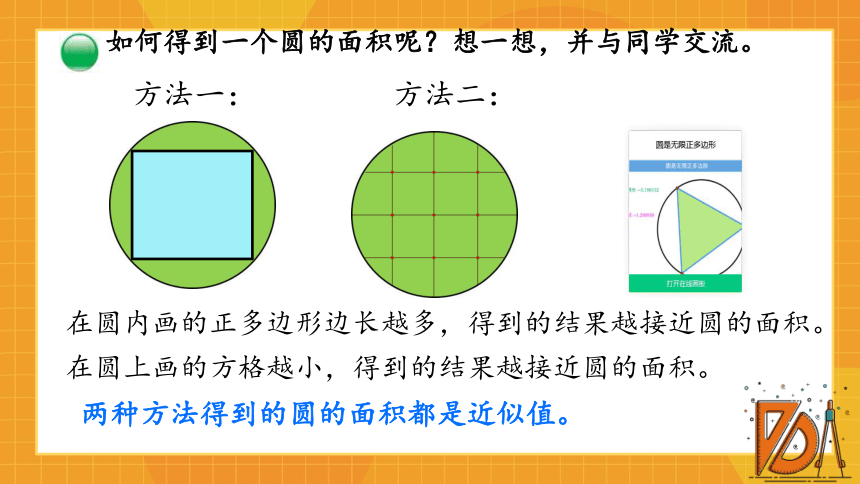
如何得到一个圆的面积呢?想一想,并与同学交流。
方法一:
方法二:
两种方法得到的圆的面积都是近似值。
在圆上画的方格越小,得到的结果越接近圆的面积。
在圆内画的正多边形边长越多,得到的结果越接近圆的面积。
能否将圆转化成以前学过的图形呢?
活动:想一想,圆的面积和什么图形有关?
4人一组,用手上的工具,动手试一试!
圆的面积公式的推导
1
平均分成8份
2
平均分成16份
3
平均分成32份
4
平均分成64份
圆的面积公式的推导
随着等分份数的不断增加,你有什么发现?
把一个圆平均分的份数( ),拼成的图形越接近长方形。
圆等分的份数越多,拼出的图形就越行四边形。
拼成的平行四边形与原来圆之间有什么联系?
拼成的平行四边形与原来的圆之间有什么联系?
(=πr)
r
宽
长方形
长
圆的周长的一半就是长方形的长
把圆剪拼成近似长方形后( )变了,( )没变。长方形的宽近似( ),长近似于( )。
圆周长的一半
圆的半径
因为长方形的面积=( )×( )
所以圆面积=( )×( )=( )
长
宽
πr
r
πr
用S表示圆的面积,圆的面积计算公式就是:
S=πr
C2
形状
面积
圆的面积=平行四边形面积
底 × 高
周长的一半
半径
圆的面积计算公式:
基础巩固
1.求下列圆的面积
2cm
6cm
S=
=3.14×22
=12.56(cm2)
3.14×32=28.26(cm2)
6÷2=3(cm)
2.看一看,比一比,你发现了什么?
圆的面积比圆外的正方形面积小,比圆内的正方形面积大……
正多边形的边数越多,越接近圆的面积。
1.若唐僧坐在圆的中心,他到圆上任意一点的距离为2米,那么唐僧在圈内的活动范围有多大呢?
=3.14×22
=3.14×4
=12.56(平方米)
答:它的面积是12.56平方米。
巩固练习
2.右图是一面我国清世祖顺治年间所铸铜钱,直径约20毫米,中间的正方形边长为6毫米。这个铜钱的面积是多少?
答:铜钱的面积是278平方毫米。
r=d÷2
=20÷2
=10(毫米)
=3.14×10×10
=314(平方毫米)
6×6=36(平方毫米)
314-36=278(平方毫米)
这节课你有什么收获?
圆的面积(一)
回忆一下,平行四边形的面积公式是怎样推导出来的
原来平行四边形的底
(长方形的长)
平行四边形等图形的面积计算公式是怎样推导得出的?
h
a
h
a
都用了“转化”的方法。
h
a
h
a
我们学过哪些图形的面积呢 是怎样推导的?
平行四边形的面积=底×高
三角形的面积=底×高÷2
梯形的面积=(上底+下底)×高÷2
转化
什么是面积呢?
面积就是图形所占平面的大小。
圆的面积就是圆所占平面的大小。
探究体验,经历过程
能否将圆转化成以前学过的图形呢?
长方形、平行四边形、梯形的面积公式是怎么推导的呢?
数格子
割补法
拼凑法
转化思想
如何得到一个圆的面积呢?
如何得到一个圆的面积呢?想一想,并与同学交流。
方法一:
方法二:
两种方法得到的圆的面积都是近似值。
在圆上画的方格越小,得到的结果越接近圆的面积。
在圆内画的正多边形边长越多,得到的结果越接近圆的面积。
能否将圆转化成以前学过的图形呢?
活动:想一想,圆的面积和什么图形有关?
4人一组,用手上的工具,动手试一试!
圆的面积公式的推导
1
平均分成8份
2
平均分成16份
3
平均分成32份
4
平均分成64份
圆的面积公式的推导
随着等分份数的不断增加,你有什么发现?
把一个圆平均分的份数( ),拼成的图形越接近长方形。
圆等分的份数越多,拼出的图形就越行四边形。
拼成的平行四边形与原来圆之间有什么联系?
拼成的平行四边形与原来的圆之间有什么联系?
(=πr)
r
宽
长方形
长
圆的周长的一半就是长方形的长
把圆剪拼成近似长方形后( )变了,( )没变。长方形的宽近似( ),长近似于( )。
圆周长的一半
圆的半径
因为长方形的面积=( )×( )
所以圆面积=( )×( )=( )
长
宽
πr
r
πr
用S表示圆的面积,圆的面积计算公式就是:
S=πr
C2
形状
面积
圆的面积=平行四边形面积
底 × 高
周长的一半
半径
圆的面积计算公式:
基础巩固
1.求下列圆的面积
2cm
6cm
S=
=3.14×22
=12.56(cm2)
3.14×32=28.26(cm2)
6÷2=3(cm)
2.看一看,比一比,你发现了什么?
圆的面积比圆外的正方形面积小,比圆内的正方形面积大……
正多边形的边数越多,越接近圆的面积。
1.若唐僧坐在圆的中心,他到圆上任意一点的距离为2米,那么唐僧在圈内的活动范围有多大呢?
=3.14×22
=3.14×4
=12.56(平方米)
答:它的面积是12.56平方米。
巩固练习
2.右图是一面我国清世祖顺治年间所铸铜钱,直径约20毫米,中间的正方形边长为6毫米。这个铜钱的面积是多少?
答:铜钱的面积是278平方毫米。
r=d÷2
=20÷2
=10(毫米)
=3.14×10×10
=314(平方毫米)
6×6=36(平方毫米)
314-36=278(平方毫米)
这节课你有什么收获?
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
