2026年中考数学一轮复习 概率(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 概率(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2026年中考数学一轮复习 概率
一.选择题(共10小题)
1.(2025 武汉)掷两个质地均匀的小正方体,小正方体的六个面上分别标有1到6的数字.下列事件是必然事件的是( )
A.向上两面的数字和为5
B.向上两面的数字和大于1
C.向上两面的数字和大于12
D.向上两面的数字和为偶数
2.(2025 武汉)某商场开展购物抽奖促销活动,抽奖盒中装有三个小球,它们分别标有10元、20元、30元,一次性随机摸出两个小球,摸出的两球上金额的和为50元的概率是( )
A. B. C. D.
3.(2025 普兰店区一模)在CASIO计算器中,RanInt#表示随机整数,输入RanInt#(a,b)(a,b是整数,且满足a<b)会随机输出一个整数x,满足a≤x≤b.若输入RanInt#[RanInt#(1,3),RanInt#(2,4)],则计算器输入一个大于2的整数x的概率是( )
A. B. C. D.
4.(2025 昆明模拟)下列事件中,属于必然事件的是( )
A.在一个装有白球和红球的袋子里摸出黑球
B.篮球队员在罚球线投篮一次,未投中
C.掷一枚硬币,正面朝上
D.如果a=b,b=c,那么a=c
5.(2025 齐齐哈尔四模)下列说法错误的是( )
A.20张票中有1张奖票,20人去摸,先摸的人摸到奖票的概率较大
B.从1,2,3,4,5中随机抽取一个数,取得奇数的可能性较大
C.小明一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次不一定有1次正面朝上
6.(2025 柳南区三模)下列事件中,必然事件的是( )
A.掷一枚硬币,恰好是国徽面朝上
B.某同学投篮球,一定投不中
C.经过红绿灯路口时,一定是绿灯
D.画一个三角形,其内角和为180°
7.(2025 济源模拟)如图是第九届亚洲冬季运动会正六边形纪念币的背面图案,小明将该图案做成转盘(转盘质地均匀),正六边形被分为六个全等的区域,每个区域上的图案不同,固定指针,转动转盘两次,任其自由停止(指针指向分界线时,不计,重转),则指针两次指向的图案相同的概率为( )
A. B. C. D.
8.(2025 孝义市三模)今年春季,为方便游客赏花,某市推出4条赏花线路,分别是:A市城区春日踏青游;B乡村田园赏春游;C山野古风漫步游;D太行风光暖阳游.小丽和妈妈计划分别从这4条线路中随机选择一条去踏青赏花,则两人选择的线路相同的概率是( )
A. B. C. D.
9.(2025 河南校级三模)小陆和小柒两位同学计划乘动车外出旅游.在网上购票时,他们选定的车厢只剩一排有余座(如图).若此时C座已售出,其余座位由系统随机分配,则这两位同学相邻而坐的概率是( )
A. B. C. D.
10.(2025 庐江县二模)五一期间,新上映的一部动漫电影深受中学生的喜爱,爸爸购得此电影票一张,姐姐、哥哥和妹妹三人都想去看,于是爸爸抛出两枚均匀的色子,将两枚色子点数相加后除以3,规定:当正好整除时姐姐去,当余数是1时哥哥去,当余数是2时妹妹去.这个游戏( )
A.是公平的 B.有利于姐姐
C.有利于哥哥 D.有利于妹妹
二.填空题(共5小题)
11.(2025 大同模拟)如图的四枚邮票分别取材于四大名著《水浒传》《三国演义》《西游记》及《红楼梦》,除正面图案外完全相同.现将四枚邮票背面朝上放置,搅匀后从中一次性随机抽取两枚,则其中有一枚邮票上的图案取材于《水浒传》的概率是 .
12.(2025 碧江区 校级模拟)一个仅装有球的不透明布袋里只有2个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n= .
13.(2025 鸡西一模)李子柴推广漆器、竹编、蜀锦、绒花、木雕这5种非遗项目要做短视频.如果每次选择2种非遗项目混搭进行短视频创作(不论顺序),那么恰好选择漆器和蜀锦混搭进行短视频创作的概率为 .
14.(2025 和平区二模)小亮了解了祖冲之、刘徽、赵爽、杨辉这4位著名数学家的生平简介,知晓他们取得的伟大成就对我国乃至世界数学发展起到的巨大推进作用,准备在数学课上随机选取其中一位的成就进行分享,选到数学家刘徽的概率是 .
15.(2025 凌河区校级三模)如图,一博物馆由圆形主馆A和三个圆形副馆B,C,D组成.一游客从主馆进入,准备参观主馆和一个副馆后离开,已知他随机从副馆四个出口中的一个离开,则他从中间出口(即出口e.f)离开的概率是 .
三.解答题(共5小题)
16.(2025 昌邑区校级三模)十二生肖是我国历史悠久的民俗文化符号,是十二地支的形象化代表,根据文献资料记载,最早并广为流传的完整十二生肖循环,是由东汉王充在公元1世纪期间所著《论衡》中提出的.下列三幅十二生肖图片,大小、形状、质地完全相同,将其洗匀,背面朝上放置.
(1)小明从中随机抽取一张,恰好抽到“蛇”的概率是 ;
(2)小丽从中随机抽取一张后并放回,再从中随机抽取一张,请用画树状图(或列表)的方法,求小丽抽取的两张图片恰好是“龙”和“蛇”的概率.
17.(2025 永寿县校级模拟)用于观测日出方位和捕捉星辰轨迹的陶寺遗址观象台,是迄今发现的世界最早的天文观测系统,能够精准划分出20个节令,这些节令是传统二十四节气的主要源头.某班语文老师决定从“A.惊蛰,B.清明,C.芒种,D.白露,E.冬至”这五个节气中随机选取主题,布置一次综合实践作业.
(1)若随机选取一个主题,则选中“E.冬至”的概率是 ;
(2)若随机选取两个主题,请利用画树状图或列表的方法,求选取的两个主题是“A.惊蛰,D.白露”的概率.
18.(2025 青阳县模拟)项目式学习
【项目背景】
为支持乡村振兴,某班级同学在老师的带领下前往某乡开展综合实践活动,其中一个项目是调查该乡农民去年每户的年收入(记为户年收入x),为乡村振兴工作提供参考.
【数据收集与整理】
该乡从几十个村中随机选取四个作为样本供调研,班级同学将这四个村编号为A,B,C,D,经过随机选取恰好选取A,B两村作深层次调研,C,D两村作浅层次调研.在A,B两村中各随机选取了25户农民的户年收入(单位:万元),在C,D两村中各随机选取了10户农民的户年收入(单位:万元),并对数据进行整理,下面给出部分信息:
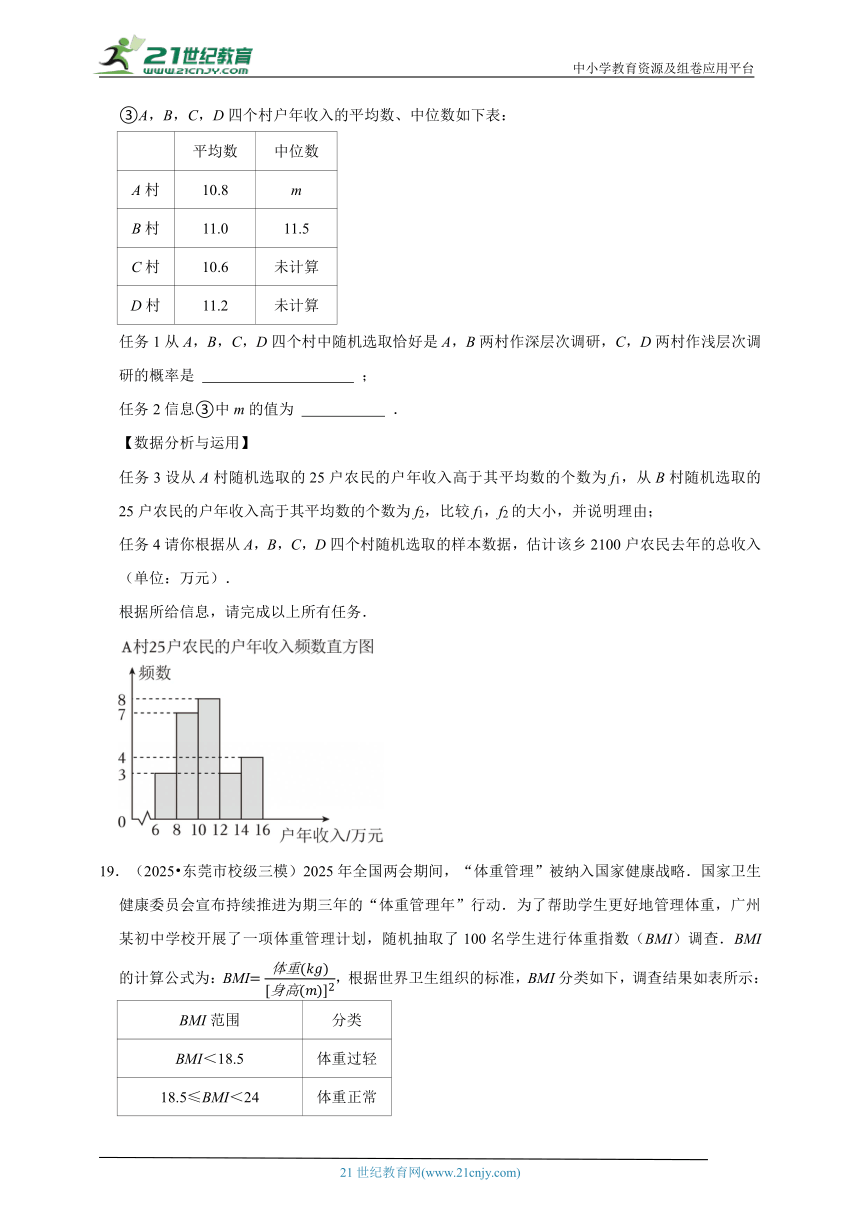
①A村25户农民的户年收入的频数分布直方图如图(数据分成5组:6≤x<8,8≤x<10,10≤x<12,12≤x<14,14≤x<16);
②A村25户农民的户年收入在10≤x<12这一组的是:10.0,10.0,10.1,10.9,11.4,11.5,11.6,11.8.
③A,B,C,D四个村户年收入的平均数、中位数如下表:
平均数 中位数
A村 10.8 m
B村 11.0 11.5
C村 10.6 未计算
D村 11.2 未计算
任务1从A,B,C,D四个村中随机选取恰好是A,B两村作深层次调研,C,D两村作浅层次调研的概率是 ;
任务2信息③中m的值为 .
【数据分析与运用】
任务3设从A村随机选取的25户农民的户年收入高于其平均数的个数为f1,从B村随机选取的25户农民的户年收入高于其平均数的个数为f2,比较f1,f2的大小,并说明理由;
任务4请你根据从A,B,C,D四个村随机选取的样本数据,估计该乡2100户农民去年的总收入(单位:万元).
根据所给信息,请完成以上所有任务.
19.(2025 东莞市校级三模)2025年全国两会期间,“体重管理”被纳入国家健康战略.国家卫生健康委员会宣布持续推进为期三年的“体重管理年”行动.为了帮助学生更好地管理体重,广州某初中学校开展了一项体重管理计划,随机抽取了100名学生进行体重指数(BMI)调查.BMI的计算公式为:BMI,根据世界卫生组织的标准,BMI分类如下,调查结果如表所示:
BMI范围 分类
BMI<18.5 体重过轻
18.5≤BMI<24 体重正常
24≤BMI<28 超重
BMI≥28 肥胖
分类 人数
体重过轻 10
体重正常 50
超重 30
肥胖 10
(1)小明身高为1.6m,BMI指数为20,则小明的体重为 kg;
(2)以下是部分统计图表,请根据表格数据补齐空缺部分.
(3)学校计划从体重正常的2个男生和2个女生中,抽取2名学生介绍体重管理经验,求抽取出来的学生恰好是一男一女的概率.
20.(2025 定西模拟)5月18日是国际博物馆日,为了解甘肃省博物馆的藏品及其承载的历史,弘扬传统文化,小英和小丽准备从博物馆的三个展厅中随机选择一个展厅报名当志愿者,三个展厅如下,分别用A,B,C表示三张形状相同的卡片,其中“A.甘肃佛教艺术展”“B.甘肃古生物化石展”“C.甘肃彩陶展”.现将这3张卡片背面朝上,洗匀放好,小英从中随机抽取一张,记下卡片,放回并洗匀后,小丽再从中随机抽取一张.
(1)小英抽到“A.甘肃佛教艺术展”展厅的概率为 ;
(2)用列表法或画树状图法求出两人恰好抽到“B.甘肃古生物化石展”和“C.甘肃彩陶展”两个展厅的概率.
2026年中考数学一轮复习 概率
参考答案与试题解析
一.选择题(共10小题)
1.(2025 武汉)掷两个质地均匀的小正方体,小正方体的六个面上分别标有1到6的数字.下列事件是必然事件的是( )
A.向上两面的数字和为5
B.向上两面的数字和大于1
C.向上两面的数字和大于12
D.向上两面的数字和为偶数
【考点】随机事件.
【专题】概率及其应用;数据分析观念.
【答案】B
【分析】事先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,必然事件和不可能事件都是确定的;在一定条件下,可能发生也可能不发生的事件,称为随机事件;据此进行判断即可.
【解答】解:掷两个质地均匀的小正方体,小正方体的六个面上分别标有1到6的数字,
向上两面的数字和为5是随机事件,则A不符合题意,
向上两面的数字和大于1是必然事件,则B符合题意,
向上两面的数字和大于12是不可能事件,则C不符合题意,
向上两面的数字和为偶数是随机事件,则D不符合题意,
故选:B.
【点评】本题考查随机事件,熟练掌握相关定义是解题的关键.
2.(2025 武汉)某商场开展购物抽奖促销活动,抽奖盒中装有三个小球,它们分别标有10元、20元、30元,一次性随机摸出两个小球,摸出的两球上金额的和为50元的概率是( )
A. B. C. D.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;运算能力.
【答案】C
【分析】用树状图表示从标有10元、20元、30元的三个小球中,随机摸出两个小球,所有等可能出现的结果,再根据概率的定义进行计算即可.
【解答】解:从标有10元、20元、30元的三个小球中,随机摸出两个小球,所有等可能出现的结果如下:
共有6种等可能出现的结果,其中两球上金额的和为50元的有2种,
所以两球上金额的和为50元的概率是.
故选:C.
【点评】本题考查列表法和树状图法,列举出从标有10元、20元、30元的三个小球中,随机摸出两个小球,所有等可能出现的结果是正确解答的关键.
3.(2025 普兰店区一模)在CASIO计算器中,RanInt#表示随机整数,输入RanInt#(a,b)(a,b是整数,且满足a<b)会随机输出一个整数x,满足a≤x≤b.若输入RanInt#[RanInt#(1,3),RanInt#(2,4)],则计算器输入一个大于2的整数x的概率是( )
A. B. C. D.
【考点】列表法与树状图法;计算器—基础知识.
【专题】概率及其应用;应用意识.
【答案】B
【分析】由题意知,共有4种等可能的结果,其中计算器输入一个大于2的整数x的结果结果有2种,结合概率公式可得答案.
【解答】解:由题意得,RanInt#(1,3)输出的整数x的取值范围为1≤x≤3,RanInt#(2,4)输出的整数x的取值范围为2≤x≤4,
∴计算器输入的结果有:1,2,3,4,共4种,其中计算器输入一个大于2的整数x的结果有:3,4,共2种,
∴计算器输入一个大于2的整数x的概率是.
故选:B.
【点评】本题考查列表法与树状图法、计算器—基础知识,熟练掌握列表法与树状图法是解答本题的关键.
4.(2025 昆明模拟)下列事件中,属于必然事件的是( )
A.在一个装有白球和红球的袋子里摸出黑球
B.篮球队员在罚球线投篮一次,未投中
C.掷一枚硬币,正面朝上
D.如果a=b,b=c,那么a=c
【考点】随机事件.
【专题】概率及其应用;数据分析观念.
【答案】D
【分析】事先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,必然事件和不可能事件都是确定的;在一定条件下,可能发生也可能不发生的事件,称为随机事件;据此进行判断即可.
【解答】解:在一个装有白球和红球的袋子里摸出黑球是不可能事件,则A不符合题意,
篮球队员在罚球线投篮一次,未投中是随机事件,则B不符合题意,
掷一枚硬币,正面朝上是随机事件,则C不符合题意,
如果a=b,b=c,那么a=c是必然事件,则D符合题意,
故选:D.
【点评】本题考查随机事件,熟练掌握其定义是解题的关键.
5.(2025 齐齐哈尔四模)下列说法错误的是( )
A.20张票中有1张奖票,20人去摸,先摸的人摸到奖票的概率较大
B.从1,2,3,4,5中随机抽取一个数,取得奇数的可能性较大
C.小明一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次不一定有1次正面朝上
【考点】概率的意义;概率公式;随机事件.
【专题】概率及其应用;数据分析观念.
【答案】A
【分析】由题意根据事件的可能性以及事件发生的概率对各选项进行依次判断即可.
【解答】解:A.20张票中有1张奖票,20人去摸,每个人摸到奖票的概率一样,符合题意;
B.从1,2,3,4,5中随机抽取一个数,取得奇数的可能性较大,不符合题意;
C.小明一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件,不符合题意;
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次不一定有1次正面朝上,不符合题意.
故选:A.
【点评】本题考查了随机事件,概率的意义,概率的公式,掌握相应的定义是关键.
6.(2025 柳南区三模)下列事件中,必然事件的是( )
A.掷一枚硬币,恰好是国徽面朝上
B.某同学投篮球,一定投不中
C.经过红绿灯路口时,一定是绿灯
D.画一个三角形,其内角和为180°
【考点】随机事件;三角形内角和定理.
【答案】D
【分析】必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.根据事件发生的可能性大小判断即可.
【解答】解:根据必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件判断如下:
A、掷一枚硬币,恰好是国徽面朝上,是随机事件,不符合题意;
B、某同学投篮球,一定投不中,是随机事件,不符合题意;
C、经过红绿灯路口时,一定是绿灯,是随机事件,不符合题意;
D、画一个三角形,其内角和为180°,是必然事件,符合题意.
故选:D.
【点评】本题考查的是必然事件、不可能事件、随机事件的概念,正确记忆相关概念是解题关键.
7.(2025 济源模拟)如图是第九届亚洲冬季运动会正六边形纪念币的背面图案,小明将该图案做成转盘(转盘质地均匀),正六边形被分为六个全等的区域,每个区域上的图案不同,固定指针,转动转盘两次,任其自由停止(指针指向分界线时,不计,重转),则指针两次指向的图案相同的概率为( )
A. B. C. D.
【考点】列表法与树状图法;全等图形;概率公式.
【专题】概率及其应用;应用意识.
【答案】B
【分析】列表可得出所有等可能的结果数以及指针两次指向的图案相同的结果数,再利用概率公式可得出答案.
【解答】解:将六个全等的区域分别记为1,2,3,4,5,6,
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
共36种等可能的结果,其中指针两次指向的图案相同的结果有6种,
∴指针两次指向的图案相同的概率为.
故选:B.
【点评】本题考查列表法与树状图法、全等图形、概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
8.(2025 孝义市三模)今年春季,为方便游客赏花,某市推出4条赏花线路,分别是:A市城区春日踏青游;B乡村田园赏春游;C山野古风漫步游;D太行风光暖阳游.小丽和妈妈计划分别从这4条线路中随机选择一条去踏青赏花,则两人选择的线路相同的概率是( )
A. B. C. D.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;应用意识.
【答案】C
【分析】列表可得出所有等可能的结果数以及两人选择的线路相同的结果数,再利用概率公式可得出答案.
【解答】解:列表如下:
A B C D
A (A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中两人选择的线路相同的结果有4种,
∴两人选择的线路相同的概率为.
故选:C.
【点评】本题考查列表法与树状图法、概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
9.(2025 河南校级三模)小陆和小柒两位同学计划乘动车外出旅游.在网上购票时,他们选定的车厢只剩一排有余座(如图).若此时C座已售出,其余座位由系统随机分配,则这两位同学相邻而坐的概率是( )
A. B. C. D.
【考点】列表法与树状图法.
【专题】概率及其应用;数据分析观念.
【答案】D
【分析】列表可得出所有等可能的结果数以及两位同学相邻而坐的结果数,再利用概率公式可得出答案.
【解答】解:列表如下:
A B D F
A (A,B) (A,D) (A,F)
B (B,A) (B,D) (B,F)
D (D,A) (D,B) (D,F)
F (F,A) (F,B) (F,D)
共有12种等可能的结果,其中这两位同学相邻而坐的结果有:(A,B),(B,A),(D,F),(F,D),共4种,
∴这两位同学相邻而坐的概率为,
故选:D.
【点评】本题考查列表法与树状图法,熟练掌握列表法与树状图法是解答本题的关键.
10.(2025 庐江县二模)五一期间,新上映的一部动漫电影深受中学生的喜爱,爸爸购得此电影票一张,姐姐、哥哥和妹妹三人都想去看,于是爸爸抛出两枚均匀的色子,将两枚色子点数相加后除以3,规定:当正好整除时姐姐去,当余数是1时哥哥去,当余数是2时妹妹去.这个游戏( )
A.是公平的 B.有利于姐姐
C.有利于哥哥 D.有利于妹妹
【考点】游戏公平性;数的整除;列表法与树状图法.
【专题】概率及其应用;应用意识.
【答案】A
【分析】根据同时掷两枚色子,其点数之和的结果列表,得到共有36种等可能结果,其中点数之和正好能被3整除的有12种,点数之和除以3后余数是1的有12种,点数之和除以3后余数是2的有12种,根据概率公式即可得到结论.
【解答】解:同时掷两枚色子,其点数之和的结果如下表所示:
第二枚两枚色子的和第一枚 1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
由表格可知,共有36种等可能结果,其中点数之和正好能被3整除的有12种,点数之和除以3后余数是1的有12种,点数之和除以3后余数是2的有12种,
哥哥获得电影票的概率是,姐姐获得电影票的概率是,妹妹获得电影票的概率是,
所以这个游戏是公平的.
故选:A.
【点评】本题考查了游戏的公平性,列表法和树状图法,正确地求出概率是解题的关键.
二.填空题(共5小题)
11.(2025 大同模拟)如图的四枚邮票分别取材于四大名著《水浒传》《三国演义》《西游记》及《红楼梦》,除正面图案外完全相同.现将四枚邮票背面朝上放置,搅匀后从中一次性随机抽取两枚,则其中有一枚邮票上的图案取材于《水浒传》的概率是 .
【考点】列表法与树状图法.
【专题】概率及其应用;数据分析观念.
【答案】.
【分析】列表法和树状图法是常用求概率的方法,使用的前提是每一种结果出现的可能性是均等的,即是等可能事件.
【解答】解:设《水浒传》《三国演义》《西游记》及《红楼梦》分别为A,B,C,D,
列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
共有12种等可能出现的结果,其中有一枚邮票上的图案取材于《水浒传》有6中,
所以其中有一枚邮票上的图案取材于《水浒传》的概率是,
故答案为:.
【点评】此题考查随机事件发生概率的计算方法,熟练掌握该知识点是关键.
12.(2025 碧江区 校级模拟)一个仅装有球的不透明布袋里只有2个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n= 3 .
【考点】概率公式.
【专题】概率及其应用;数据分析观念.
【答案】3.
【分析】根据概率公式列方程,解方程即可.
【解答】解:根据概率公式列方程得,
解得n=3,
故答案为:3.
【点评】本题考查已知概率求数量,解题的关键是掌握概率公式.
13.(2025 鸡西一模)李子柴推广漆器、竹编、蜀锦、绒花、木雕这5种非遗项目要做短视频.如果每次选择2种非遗项目混搭进行短视频创作(不论顺序),那么恰好选择漆器和蜀锦混搭进行短视频创作的概率为 .
【考点】列表法与树状图法.
【专题】推理填空题;推理能力.
【答案】.
【分析】先列出所有情况,再求出选择漆器和蜀锦的概率.
【解答】解:列出所有可能的选择情况,设5种非遗项目为:漆器(A)、蜀锦(B)、其他3种分别为C、D、E.从5种中选2种,所有可能的组合有:(A,B)、(A,C)、(A,D)、(A,E)、(B,C)、(B,D)、(B,E)、(C,D)、(C,E)、(D,E),共10种等可能的情况.恰好选择漆器和蜀锦的情况只有1种:(A,B).概率 = 符合条件的情况数÷总情况数.
故答案为:.
【点评】本题结合非遗项目,考查概率问题.
14.(2025 和平区二模)小亮了解了祖冲之、刘徽、赵爽、杨辉这4位著名数学家的生平简介,知晓他们取得的伟大成就对我国乃至世界数学发展起到的巨大推进作用,准备在数学课上随机选取其中一位的成就进行分享,选到数学家刘徽的概率是 .
【考点】概率公式.
【专题】概率及其应用;数据分析观念.
【答案】见试题解答内容
【分析】直接根据概率公式求解即可.
【解答】解:随机选取其中一位的成就进行分享,选到数学家刘徽的概率是,
故答案为:.
【点评】本题主要考查概率公式,随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
15.(2025 凌河区校级三模)如图,一博物馆由圆形主馆A和三个圆形副馆B,C,D组成.一游客从主馆进入,准备参观主馆和一个副馆后离开,已知他随机从副馆四个出口中的一个离开,则他从中间出口(即出口e.f)离开的概率是 .
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】.
【分析】画树状图,共有6种等可能的结果,其中从中间出口(即出口e,f)离开的结果有4种,再由概率公式求解即可.
【解答】解:画树状图如下:
由树状图可知:从中间出口(即出口e,f)离开的结果有4种,
∴他从中间出口(即出口e,f)离开的概率是,
故答案为:.
【点评】本题考查了列表法与树状图法求概率,掌握知识点的应用是解题的关键.
三.解答题(共5小题)
16.(2025 昌邑区校级三模)十二生肖是我国历史悠久的民俗文化符号,是十二地支的形象化代表,根据文献资料记载,最早并广为流传的完整十二生肖循环,是由东汉王充在公元1世纪期间所著《论衡》中提出的.下列三幅十二生肖图片,大小、形状、质地完全相同,将其洗匀,背面朝上放置.
(1)小明从中随机抽取一张,恰好抽到“蛇”的概率是 ;
(2)小丽从中随机抽取一张后并放回,再从中随机抽取一张,请用画树状图(或列表)的方法,求小丽抽取的两张图片恰好是“龙”和“蛇”的概率.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】(1);
(2)见解析,.
【分析】(1)根据题意求解即可;
(2)画树状图可得出所有等可能的结果数以及两张图片恰好是“龙”和“蛇”的结果数,再利用概率公式可得出答案.
【解答】解:(1)小明从中随机抽取一张,恰好抽到“蛇”的概率是,
故答案为:;
(2)根据题意,令三张图片为A,B,C,从中随机抽取一张后并放回,再从中随机抽取一张,作树状图如下:
共有9种等可能的结果,其中小丽抽取的两张图片恰好是“龙”和“蛇”的结果有2种,
∴P(小丽抽取的两张图片恰好是“龙”和“蛇”).
【点评】本题考查列表法与树状图法,概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
17.(2025 永寿县校级模拟)用于观测日出方位和捕捉星辰轨迹的陶寺遗址观象台,是迄今发现的世界最早的天文观测系统,能够精准划分出20个节令,这些节令是传统二十四节气的主要源头.某班语文老师决定从“A.惊蛰,B.清明,C.芒种,D.白露,E.冬至”这五个节气中随机选取主题,布置一次综合实践作业.
(1)若随机选取一个主题,则选中“E.冬至”的概率是 ;
(2)若随机选取两个主题,请利用画树状图或列表的方法,求选取的两个主题是“A.惊蛰,D.白露”的概率.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】(1);
(2).
【分析】(1)根据题意,可以得到随机选取一个主题,则选中“E.冬至”的概率;
(2)根据题意可以画出相应的表格,然后即可得到选取的两个主题是“A.惊蛰,D.白露”的概率.
【解答】解:(1)由题意可得,
随机选取一个主题,则选中“E.冬至”的概率是,
故答案为:;
(2)根据题意,列表如下:
第一个 第二个
A B C D E
A 一 (A,B) (A,C) (A,D) (A,E)
B (B,A) 一 (B,C) (B,D) (B,E)
C (C,A) (C,B) 一 (C,D) (C,E)
D (D,A) (D,B) (D,C) 一 (D,E)
E (E,A) (E,B) (E,C) (E,D) 一
由列表可知,共有20种等可能的结果,其中选取的两个主题是“A.惊蛰,D.白露”的结果有2种,
∴选取的两个主题是“A.惊蛰,D.白露”的概率是.
【点评】本题考查列表法与树状图法、概率公式,解答本题的关键是明确题意,列出相应的表格,求出相应的概率.
18.(2025 青阳县模拟)项目式学习
【项目背景】
为支持乡村振兴,某班级同学在老师的带领下前往某乡开展综合实践活动,其中一个项目是调查该乡农民去年每户的年收入(记为户年收入x),为乡村振兴工作提供参考.
【数据收集与整理】
该乡从几十个村中随机选取四个作为样本供调研,班级同学将这四个村编号为A,B,C,D,经过随机选取恰好选取A,B两村作深层次调研,C,D两村作浅层次调研.在A,B两村中各随机选取了25户农民的户年收入(单位:万元),在C,D两村中各随机选取了10户农民的户年收入(单位:万元),并对数据进行整理,下面给出部分信息:
①A村25户农民的户年收入的频数分布直方图如图(数据分成5组:6≤x<8,8≤x<10,10≤x<12,12≤x<14,14≤x<16);
②A村25户农民的户年收入在10≤x<12这一组的是:10.0,10.0,10.1,10.9,11.4,11.5,11.6,11.8.
③A,B,C,D四个村户年收入的平均数、中位数如下表:
平均数 中位数
A村 10.8 m
B村 11.0 11.5
C村 10.6 未计算
D村 11.2 未计算
任务1从A,B,C,D四个村中随机选取恰好是A,B两村作深层次调研,C,D两村作浅层次调研的概率是 ;
任务2信息③中m的值为 10.1 .
【数据分析与运用】
任务3设从A村随机选取的25户农民的户年收入高于其平均数的个数为f1,从B村随机选取的25户农民的户年收入高于其平均数的个数为f2,比较f1,f2的大小,并说明理由;
任务4请你根据从A,B,C,D四个村随机选取的样本数据,估计该乡2100户农民去年的总收入(单位:万元).
根据所给信息,请完成以上所有任务.
【考点】列表法与树状图法;用样本估计总体;频数(率)分布直方图;加权平均数;中位数.
【答案】任务一:
任务二:10.1;
任务三:f1<f2:
任务四:22890万元.
【分析】任务一:概率计算的关键是明确“所有可能的情况”和“符合条件的情况”,两者的比值即为概率.;
任务二:中位数是将数据按大小排列后,位于中间位置的数值,反映数据的中等水平;
任务三:结合分组数据和中位数的性质分析;
任务四:用样本的平均收入估计总体的平均收入,再乘以总户数得到总体总收入,属于“用样本估计总体”的统计思想.
【解答】解:任务一:从A、B、C、D四个村中选2个作深层次调研,所有可能的组合为:(A,B)、(A,C)、(A,D)、(B,C)、(B,D)、(C,D),共6种等可能情况.
恰好选A、B作深层次调研,C、D作浅层次调研的情况只有1种:(A,B).
概率=符合条件的情况数÷总情况数;
故答案为:;
任务二:A村共25户,中位数是按收入从小到大排列后第13户的收入.
收入 6≤x<8 的有3户,8≤x<10 的有7户,前两组共 3+7=10 户(即第1到10户).
第11到25户在 10≤x<12 及以后区间,其中 10≤x<12 有8户,
因此第13户在 10≤x<12 区间,且是该区间的第 13﹣10=3 户,对应收入为10.1.
所以 m=10.1.
故答案为:10.1;
任务三:A村平均数为10.8,12≤x<14 有4户,14≤x<16 有3户,
这两组合计 4+3=7 户,均大于10.8.
10≤x<12 共8户,其中大于10.8的有 8﹣4=4 户(前4户≤10.8).
因此f1=7+4=11.
B村中位数为11.5,说明第13户收入为11.5(大于11.0),则第13到25户共13户收入均≥11.5,自然大于11.0.
因此 f2≥13.
∴f1<f2.
任务四:样本包含A村25户、B村25户、C村10户、D村10户,
总共有 25+25+10+10=70 户.
样本总收入为:10.8×25+11.0×25+10.6×10+11.2×10=270+275+106+112=763 (万元),
样本平均收入 = 总收入÷总样本数=763÷70=10.9 (万元/户).
该乡共2100户,
总收入≈平均收入×总户数= 10.9×2100=22890 (万元).
答:该乡2100户农民去年的总收入为22890万元.
【点评】本题结合调查农民收入,考查概率问题.
19.(2025 东莞市校级三模)2025年全国两会期间,“体重管理”被纳入国家健康战略.国家卫生健康委员会宣布持续推进为期三年的“体重管理年”行动.为了帮助学生更好地管理体重,广州某初中学校开展了一项体重管理计划,随机抽取了100名学生进行体重指数(BMI)调查.BMI的计算公式为:BMI,根据世界卫生组织的标准,BMI分类如下,调查结果如表所示:
BMI范围 分类
BMI<18.5 体重过轻
18.5≤BMI<24 体重正常
24≤BMI<28 超重
BMI≥28 肥胖
分类 人数
体重过轻 10
体重正常 50
超重 30
肥胖 10
(1)小明身高为1.6m,BMI指数为20,则小明的体重为 51.2 kg;
(2)以下是部分统计图表,请根据表格数据补齐空缺部分.
(3)学校计划从体重正常的2个男生和2个女生中,抽取2名学生介绍体重管理经验,求抽取出来的学生恰好是一男一女的概率.
【考点】列表法与树状图法;扇形统计图;条形统计图;概率公式.
【专题】数据的收集与整理;概率及其应用;数据分析观念;应用意识.
【答案】(1)51.2.
(2)见解答.
(3).
【分析】(1)根据BMI的计算公式代入计算即可.
(2)由表格可知,超重的人数为30人,由扇形统计图可知,超重的百分比为1﹣50%﹣10%﹣10%=30%,补全统计图即可.
(3)列表可得出所有等可能的结果数以及抽取出来的学生恰好是一男一女的结果数,再利用概率公式可得出答案.
【解答】解:(1)∵小明身高为1.6m,BMI指数为20,
∴小明的体重为20×1.62=51.2(kg).
故答案为:51.2.
(2)由表格可知,超重的人数为30人,
扇形统计图中超重的百分比为1﹣50%﹣10%﹣10%=30%.
补全统计图如图所示.
(3)列表如下:
男 男 女 女
男 (男,男) (男,女) (男,女)
男 (男,男) (男,女) (男,女)
女 (女,男) (女,男) (女,女)
女 (女,男) (女,男) (女,女)
共有12种等可能的结果,其中抽取出来的学生恰好是一男一女的结果有8种,
∴抽取出来的学生恰好是一男一女的概率为.
【点评】本题考查列表法与树状图法、条形统计图、扇形统计图、概率公式,能够读懂统计图,掌握列表法与树状图法、概率公式是解答本题的关键.
20.(2025 定西模拟)5月18日是国际博物馆日,为了解甘肃省博物馆的藏品及其承载的历史,弘扬传统文化,小英和小丽准备从博物馆的三个展厅中随机选择一个展厅报名当志愿者,三个展厅如下,分别用A,B,C表示三张形状相同的卡片,其中“A.甘肃佛教艺术展”“B.甘肃古生物化石展”“C.甘肃彩陶展”.现将这3张卡片背面朝上,洗匀放好,小英从中随机抽取一张,记下卡片,放回并洗匀后,小丽再从中随机抽取一张.
(1)小英抽到“A.甘肃佛教艺术展”展厅的概率为 ;
(2)用列表法或画树状图法求出两人恰好抽到“B.甘肃古生物化石展”和“C.甘肃彩陶展”两个展厅的概率.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】(1)
(2)
【分析】(1)直接利用概率公式计算即可;
(2)先列表得到所有结果,找出符合条件的结果利用概率公式计算即可.
【解答】解:(1)∵共有“A.甘肃佛教艺术展”“B.甘肃古生物化石展”“C.甘肃彩陶展”三种等可能的情况,
∴小英从中随机抽取一张,小英抽到“A.甘肃佛教艺术展”展厅的概率为,
故答案为:;
(2)小英从三张形状相同的卡片随机抽取一张,放回并洗匀后,小丽再从中随机抽取一张,列表如下:
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
∴所有的等可能的结果数有9个,两人恰好抽到“B.甘肃古生物化石展”和“C.甘肃彩陶展”两个展厅的结果数有2个,
∴两人恰好抽到“B.甘肃古生物化石展”和“C.甘肃彩陶展”两个展厅的概率为.
【点评】本题主要考查了列表法与树状图法,概率公式,熟练掌握概率的求法是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年中考数学一轮复习 概率
一.选择题(共10小题)
1.(2025 武汉)掷两个质地均匀的小正方体,小正方体的六个面上分别标有1到6的数字.下列事件是必然事件的是( )
A.向上两面的数字和为5
B.向上两面的数字和大于1
C.向上两面的数字和大于12
D.向上两面的数字和为偶数
2.(2025 武汉)某商场开展购物抽奖促销活动,抽奖盒中装有三个小球,它们分别标有10元、20元、30元,一次性随机摸出两个小球,摸出的两球上金额的和为50元的概率是( )
A. B. C. D.
3.(2025 普兰店区一模)在CASIO计算器中,RanInt#表示随机整数,输入RanInt#(a,b)(a,b是整数,且满足a<b)会随机输出一个整数x,满足a≤x≤b.若输入RanInt#[RanInt#(1,3),RanInt#(2,4)],则计算器输入一个大于2的整数x的概率是( )
A. B. C. D.
4.(2025 昆明模拟)下列事件中,属于必然事件的是( )
A.在一个装有白球和红球的袋子里摸出黑球
B.篮球队员在罚球线投篮一次,未投中
C.掷一枚硬币,正面朝上
D.如果a=b,b=c,那么a=c
5.(2025 齐齐哈尔四模)下列说法错误的是( )
A.20张票中有1张奖票,20人去摸,先摸的人摸到奖票的概率较大
B.从1,2,3,4,5中随机抽取一个数,取得奇数的可能性较大
C.小明一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次不一定有1次正面朝上
6.(2025 柳南区三模)下列事件中,必然事件的是( )
A.掷一枚硬币,恰好是国徽面朝上
B.某同学投篮球,一定投不中
C.经过红绿灯路口时,一定是绿灯
D.画一个三角形,其内角和为180°
7.(2025 济源模拟)如图是第九届亚洲冬季运动会正六边形纪念币的背面图案,小明将该图案做成转盘(转盘质地均匀),正六边形被分为六个全等的区域,每个区域上的图案不同,固定指针,转动转盘两次,任其自由停止(指针指向分界线时,不计,重转),则指针两次指向的图案相同的概率为( )
A. B. C. D.
8.(2025 孝义市三模)今年春季,为方便游客赏花,某市推出4条赏花线路,分别是:A市城区春日踏青游;B乡村田园赏春游;C山野古风漫步游;D太行风光暖阳游.小丽和妈妈计划分别从这4条线路中随机选择一条去踏青赏花,则两人选择的线路相同的概率是( )
A. B. C. D.
9.(2025 河南校级三模)小陆和小柒两位同学计划乘动车外出旅游.在网上购票时,他们选定的车厢只剩一排有余座(如图).若此时C座已售出,其余座位由系统随机分配,则这两位同学相邻而坐的概率是( )
A. B. C. D.
10.(2025 庐江县二模)五一期间,新上映的一部动漫电影深受中学生的喜爱,爸爸购得此电影票一张,姐姐、哥哥和妹妹三人都想去看,于是爸爸抛出两枚均匀的色子,将两枚色子点数相加后除以3,规定:当正好整除时姐姐去,当余数是1时哥哥去,当余数是2时妹妹去.这个游戏( )
A.是公平的 B.有利于姐姐
C.有利于哥哥 D.有利于妹妹
二.填空题(共5小题)
11.(2025 大同模拟)如图的四枚邮票分别取材于四大名著《水浒传》《三国演义》《西游记》及《红楼梦》,除正面图案外完全相同.现将四枚邮票背面朝上放置,搅匀后从中一次性随机抽取两枚,则其中有一枚邮票上的图案取材于《水浒传》的概率是 .
12.(2025 碧江区 校级模拟)一个仅装有球的不透明布袋里只有2个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n= .
13.(2025 鸡西一模)李子柴推广漆器、竹编、蜀锦、绒花、木雕这5种非遗项目要做短视频.如果每次选择2种非遗项目混搭进行短视频创作(不论顺序),那么恰好选择漆器和蜀锦混搭进行短视频创作的概率为 .
14.(2025 和平区二模)小亮了解了祖冲之、刘徽、赵爽、杨辉这4位著名数学家的生平简介,知晓他们取得的伟大成就对我国乃至世界数学发展起到的巨大推进作用,准备在数学课上随机选取其中一位的成就进行分享,选到数学家刘徽的概率是 .
15.(2025 凌河区校级三模)如图,一博物馆由圆形主馆A和三个圆形副馆B,C,D组成.一游客从主馆进入,准备参观主馆和一个副馆后离开,已知他随机从副馆四个出口中的一个离开,则他从中间出口(即出口e.f)离开的概率是 .
三.解答题(共5小题)
16.(2025 昌邑区校级三模)十二生肖是我国历史悠久的民俗文化符号,是十二地支的形象化代表,根据文献资料记载,最早并广为流传的完整十二生肖循环,是由东汉王充在公元1世纪期间所著《论衡》中提出的.下列三幅十二生肖图片,大小、形状、质地完全相同,将其洗匀,背面朝上放置.
(1)小明从中随机抽取一张,恰好抽到“蛇”的概率是 ;
(2)小丽从中随机抽取一张后并放回,再从中随机抽取一张,请用画树状图(或列表)的方法,求小丽抽取的两张图片恰好是“龙”和“蛇”的概率.
17.(2025 永寿县校级模拟)用于观测日出方位和捕捉星辰轨迹的陶寺遗址观象台,是迄今发现的世界最早的天文观测系统,能够精准划分出20个节令,这些节令是传统二十四节气的主要源头.某班语文老师决定从“A.惊蛰,B.清明,C.芒种,D.白露,E.冬至”这五个节气中随机选取主题,布置一次综合实践作业.
(1)若随机选取一个主题,则选中“E.冬至”的概率是 ;
(2)若随机选取两个主题,请利用画树状图或列表的方法,求选取的两个主题是“A.惊蛰,D.白露”的概率.
18.(2025 青阳县模拟)项目式学习
【项目背景】
为支持乡村振兴,某班级同学在老师的带领下前往某乡开展综合实践活动,其中一个项目是调查该乡农民去年每户的年收入(记为户年收入x),为乡村振兴工作提供参考.
【数据收集与整理】
该乡从几十个村中随机选取四个作为样本供调研,班级同学将这四个村编号为A,B,C,D,经过随机选取恰好选取A,B两村作深层次调研,C,D两村作浅层次调研.在A,B两村中各随机选取了25户农民的户年收入(单位:万元),在C,D两村中各随机选取了10户农民的户年收入(单位:万元),并对数据进行整理,下面给出部分信息:
①A村25户农民的户年收入的频数分布直方图如图(数据分成5组:6≤x<8,8≤x<10,10≤x<12,12≤x<14,14≤x<16);
②A村25户农民的户年收入在10≤x<12这一组的是:10.0,10.0,10.1,10.9,11.4,11.5,11.6,11.8.
③A,B,C,D四个村户年收入的平均数、中位数如下表:
平均数 中位数
A村 10.8 m
B村 11.0 11.5
C村 10.6 未计算
D村 11.2 未计算
任务1从A,B,C,D四个村中随机选取恰好是A,B两村作深层次调研,C,D两村作浅层次调研的概率是 ;
任务2信息③中m的值为 .
【数据分析与运用】
任务3设从A村随机选取的25户农民的户年收入高于其平均数的个数为f1,从B村随机选取的25户农民的户年收入高于其平均数的个数为f2,比较f1,f2的大小,并说明理由;
任务4请你根据从A,B,C,D四个村随机选取的样本数据,估计该乡2100户农民去年的总收入(单位:万元).
根据所给信息,请完成以上所有任务.
19.(2025 东莞市校级三模)2025年全国两会期间,“体重管理”被纳入国家健康战略.国家卫生健康委员会宣布持续推进为期三年的“体重管理年”行动.为了帮助学生更好地管理体重,广州某初中学校开展了一项体重管理计划,随机抽取了100名学生进行体重指数(BMI)调查.BMI的计算公式为:BMI,根据世界卫生组织的标准,BMI分类如下,调查结果如表所示:
BMI范围 分类
BMI<18.5 体重过轻
18.5≤BMI<24 体重正常
24≤BMI<28 超重
BMI≥28 肥胖
分类 人数
体重过轻 10
体重正常 50
超重 30
肥胖 10
(1)小明身高为1.6m,BMI指数为20,则小明的体重为 kg;
(2)以下是部分统计图表,请根据表格数据补齐空缺部分.
(3)学校计划从体重正常的2个男生和2个女生中,抽取2名学生介绍体重管理经验,求抽取出来的学生恰好是一男一女的概率.
20.(2025 定西模拟)5月18日是国际博物馆日,为了解甘肃省博物馆的藏品及其承载的历史,弘扬传统文化,小英和小丽准备从博物馆的三个展厅中随机选择一个展厅报名当志愿者,三个展厅如下,分别用A,B,C表示三张形状相同的卡片,其中“A.甘肃佛教艺术展”“B.甘肃古生物化石展”“C.甘肃彩陶展”.现将这3张卡片背面朝上,洗匀放好,小英从中随机抽取一张,记下卡片,放回并洗匀后,小丽再从中随机抽取一张.
(1)小英抽到“A.甘肃佛教艺术展”展厅的概率为 ;
(2)用列表法或画树状图法求出两人恰好抽到“B.甘肃古生物化石展”和“C.甘肃彩陶展”两个展厅的概率.
2026年中考数学一轮复习 概率
参考答案与试题解析
一.选择题(共10小题)
1.(2025 武汉)掷两个质地均匀的小正方体,小正方体的六个面上分别标有1到6的数字.下列事件是必然事件的是( )
A.向上两面的数字和为5
B.向上两面的数字和大于1
C.向上两面的数字和大于12
D.向上两面的数字和为偶数
【考点】随机事件.
【专题】概率及其应用;数据分析观念.
【答案】B
【分析】事先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,必然事件和不可能事件都是确定的;在一定条件下,可能发生也可能不发生的事件,称为随机事件;据此进行判断即可.
【解答】解:掷两个质地均匀的小正方体,小正方体的六个面上分别标有1到6的数字,
向上两面的数字和为5是随机事件,则A不符合题意,
向上两面的数字和大于1是必然事件,则B符合题意,
向上两面的数字和大于12是不可能事件,则C不符合题意,
向上两面的数字和为偶数是随机事件,则D不符合题意,
故选:B.
【点评】本题考查随机事件,熟练掌握相关定义是解题的关键.
2.(2025 武汉)某商场开展购物抽奖促销活动,抽奖盒中装有三个小球,它们分别标有10元、20元、30元,一次性随机摸出两个小球,摸出的两球上金额的和为50元的概率是( )
A. B. C. D.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;运算能力.
【答案】C
【分析】用树状图表示从标有10元、20元、30元的三个小球中,随机摸出两个小球,所有等可能出现的结果,再根据概率的定义进行计算即可.
【解答】解:从标有10元、20元、30元的三个小球中,随机摸出两个小球,所有等可能出现的结果如下:
共有6种等可能出现的结果,其中两球上金额的和为50元的有2种,
所以两球上金额的和为50元的概率是.
故选:C.
【点评】本题考查列表法和树状图法,列举出从标有10元、20元、30元的三个小球中,随机摸出两个小球,所有等可能出现的结果是正确解答的关键.
3.(2025 普兰店区一模)在CASIO计算器中,RanInt#表示随机整数,输入RanInt#(a,b)(a,b是整数,且满足a<b)会随机输出一个整数x,满足a≤x≤b.若输入RanInt#[RanInt#(1,3),RanInt#(2,4)],则计算器输入一个大于2的整数x的概率是( )
A. B. C. D.
【考点】列表法与树状图法;计算器—基础知识.
【专题】概率及其应用;应用意识.
【答案】B
【分析】由题意知,共有4种等可能的结果,其中计算器输入一个大于2的整数x的结果结果有2种,结合概率公式可得答案.
【解答】解:由题意得,RanInt#(1,3)输出的整数x的取值范围为1≤x≤3,RanInt#(2,4)输出的整数x的取值范围为2≤x≤4,
∴计算器输入的结果有:1,2,3,4,共4种,其中计算器输入一个大于2的整数x的结果有:3,4,共2种,
∴计算器输入一个大于2的整数x的概率是.
故选:B.
【点评】本题考查列表法与树状图法、计算器—基础知识,熟练掌握列表法与树状图法是解答本题的关键.
4.(2025 昆明模拟)下列事件中,属于必然事件的是( )
A.在一个装有白球和红球的袋子里摸出黑球
B.篮球队员在罚球线投篮一次,未投中
C.掷一枚硬币,正面朝上
D.如果a=b,b=c,那么a=c
【考点】随机事件.
【专题】概率及其应用;数据分析观念.
【答案】D
【分析】事先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,必然事件和不可能事件都是确定的;在一定条件下,可能发生也可能不发生的事件,称为随机事件;据此进行判断即可.
【解答】解:在一个装有白球和红球的袋子里摸出黑球是不可能事件,则A不符合题意,
篮球队员在罚球线投篮一次,未投中是随机事件,则B不符合题意,
掷一枚硬币,正面朝上是随机事件,则C不符合题意,
如果a=b,b=c,那么a=c是必然事件,则D符合题意,
故选:D.
【点评】本题考查随机事件,熟练掌握其定义是解题的关键.
5.(2025 齐齐哈尔四模)下列说法错误的是( )
A.20张票中有1张奖票,20人去摸,先摸的人摸到奖票的概率较大
B.从1,2,3,4,5中随机抽取一个数,取得奇数的可能性较大
C.小明一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次不一定有1次正面朝上
【考点】概率的意义;概率公式;随机事件.
【专题】概率及其应用;数据分析观念.
【答案】A
【分析】由题意根据事件的可能性以及事件发生的概率对各选项进行依次判断即可.
【解答】解:A.20张票中有1张奖票,20人去摸,每个人摸到奖票的概率一样,符合题意;
B.从1,2,3,4,5中随机抽取一个数,取得奇数的可能性较大,不符合题意;
C.小明一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件,不符合题意;
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次不一定有1次正面朝上,不符合题意.
故选:A.
【点评】本题考查了随机事件,概率的意义,概率的公式,掌握相应的定义是关键.
6.(2025 柳南区三模)下列事件中,必然事件的是( )
A.掷一枚硬币,恰好是国徽面朝上
B.某同学投篮球,一定投不中
C.经过红绿灯路口时,一定是绿灯
D.画一个三角形,其内角和为180°
【考点】随机事件;三角形内角和定理.
【答案】D
【分析】必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.根据事件发生的可能性大小判断即可.
【解答】解:根据必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件判断如下:
A、掷一枚硬币,恰好是国徽面朝上,是随机事件,不符合题意;
B、某同学投篮球,一定投不中,是随机事件,不符合题意;
C、经过红绿灯路口时,一定是绿灯,是随机事件,不符合题意;
D、画一个三角形,其内角和为180°,是必然事件,符合题意.
故选:D.
【点评】本题考查的是必然事件、不可能事件、随机事件的概念,正确记忆相关概念是解题关键.
7.(2025 济源模拟)如图是第九届亚洲冬季运动会正六边形纪念币的背面图案,小明将该图案做成转盘(转盘质地均匀),正六边形被分为六个全等的区域,每个区域上的图案不同,固定指针,转动转盘两次,任其自由停止(指针指向分界线时,不计,重转),则指针两次指向的图案相同的概率为( )
A. B. C. D.
【考点】列表法与树状图法;全等图形;概率公式.
【专题】概率及其应用;应用意识.
【答案】B
【分析】列表可得出所有等可能的结果数以及指针两次指向的图案相同的结果数,再利用概率公式可得出答案.
【解答】解:将六个全等的区域分别记为1,2,3,4,5,6,
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
共36种等可能的结果,其中指针两次指向的图案相同的结果有6种,
∴指针两次指向的图案相同的概率为.
故选:B.
【点评】本题考查列表法与树状图法、全等图形、概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
8.(2025 孝义市三模)今年春季,为方便游客赏花,某市推出4条赏花线路,分别是:A市城区春日踏青游;B乡村田园赏春游;C山野古风漫步游;D太行风光暖阳游.小丽和妈妈计划分别从这4条线路中随机选择一条去踏青赏花,则两人选择的线路相同的概率是( )
A. B. C. D.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;应用意识.
【答案】C
【分析】列表可得出所有等可能的结果数以及两人选择的线路相同的结果数,再利用概率公式可得出答案.
【解答】解:列表如下:
A B C D
A (A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中两人选择的线路相同的结果有4种,
∴两人选择的线路相同的概率为.
故选:C.
【点评】本题考查列表法与树状图法、概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
9.(2025 河南校级三模)小陆和小柒两位同学计划乘动车外出旅游.在网上购票时,他们选定的车厢只剩一排有余座(如图).若此时C座已售出,其余座位由系统随机分配,则这两位同学相邻而坐的概率是( )
A. B. C. D.
【考点】列表法与树状图法.
【专题】概率及其应用;数据分析观念.
【答案】D
【分析】列表可得出所有等可能的结果数以及两位同学相邻而坐的结果数,再利用概率公式可得出答案.
【解答】解:列表如下:
A B D F
A (A,B) (A,D) (A,F)
B (B,A) (B,D) (B,F)
D (D,A) (D,B) (D,F)
F (F,A) (F,B) (F,D)
共有12种等可能的结果,其中这两位同学相邻而坐的结果有:(A,B),(B,A),(D,F),(F,D),共4种,
∴这两位同学相邻而坐的概率为,
故选:D.
【点评】本题考查列表法与树状图法,熟练掌握列表法与树状图法是解答本题的关键.
10.(2025 庐江县二模)五一期间,新上映的一部动漫电影深受中学生的喜爱,爸爸购得此电影票一张,姐姐、哥哥和妹妹三人都想去看,于是爸爸抛出两枚均匀的色子,将两枚色子点数相加后除以3,规定:当正好整除时姐姐去,当余数是1时哥哥去,当余数是2时妹妹去.这个游戏( )
A.是公平的 B.有利于姐姐
C.有利于哥哥 D.有利于妹妹
【考点】游戏公平性;数的整除;列表法与树状图法.
【专题】概率及其应用;应用意识.
【答案】A
【分析】根据同时掷两枚色子,其点数之和的结果列表,得到共有36种等可能结果,其中点数之和正好能被3整除的有12种,点数之和除以3后余数是1的有12种,点数之和除以3后余数是2的有12种,根据概率公式即可得到结论.
【解答】解:同时掷两枚色子,其点数之和的结果如下表所示:
第二枚两枚色子的和第一枚 1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
由表格可知,共有36种等可能结果,其中点数之和正好能被3整除的有12种,点数之和除以3后余数是1的有12种,点数之和除以3后余数是2的有12种,
哥哥获得电影票的概率是,姐姐获得电影票的概率是,妹妹获得电影票的概率是,
所以这个游戏是公平的.
故选:A.
【点评】本题考查了游戏的公平性,列表法和树状图法,正确地求出概率是解题的关键.
二.填空题(共5小题)
11.(2025 大同模拟)如图的四枚邮票分别取材于四大名著《水浒传》《三国演义》《西游记》及《红楼梦》,除正面图案外完全相同.现将四枚邮票背面朝上放置,搅匀后从中一次性随机抽取两枚,则其中有一枚邮票上的图案取材于《水浒传》的概率是 .
【考点】列表法与树状图法.
【专题】概率及其应用;数据分析观念.
【答案】.
【分析】列表法和树状图法是常用求概率的方法,使用的前提是每一种结果出现的可能性是均等的,即是等可能事件.
【解答】解:设《水浒传》《三国演义》《西游记》及《红楼梦》分别为A,B,C,D,
列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
共有12种等可能出现的结果,其中有一枚邮票上的图案取材于《水浒传》有6中,
所以其中有一枚邮票上的图案取材于《水浒传》的概率是,
故答案为:.
【点评】此题考查随机事件发生概率的计算方法,熟练掌握该知识点是关键.
12.(2025 碧江区 校级模拟)一个仅装有球的不透明布袋里只有2个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n= 3 .
【考点】概率公式.
【专题】概率及其应用;数据分析观念.
【答案】3.
【分析】根据概率公式列方程,解方程即可.
【解答】解:根据概率公式列方程得,
解得n=3,
故答案为:3.
【点评】本题考查已知概率求数量,解题的关键是掌握概率公式.
13.(2025 鸡西一模)李子柴推广漆器、竹编、蜀锦、绒花、木雕这5种非遗项目要做短视频.如果每次选择2种非遗项目混搭进行短视频创作(不论顺序),那么恰好选择漆器和蜀锦混搭进行短视频创作的概率为 .
【考点】列表法与树状图法.
【专题】推理填空题;推理能力.
【答案】.
【分析】先列出所有情况,再求出选择漆器和蜀锦的概率.
【解答】解:列出所有可能的选择情况,设5种非遗项目为:漆器(A)、蜀锦(B)、其他3种分别为C、D、E.从5种中选2种,所有可能的组合有:(A,B)、(A,C)、(A,D)、(A,E)、(B,C)、(B,D)、(B,E)、(C,D)、(C,E)、(D,E),共10种等可能的情况.恰好选择漆器和蜀锦的情况只有1种:(A,B).概率 = 符合条件的情况数÷总情况数.
故答案为:.
【点评】本题结合非遗项目,考查概率问题.
14.(2025 和平区二模)小亮了解了祖冲之、刘徽、赵爽、杨辉这4位著名数学家的生平简介,知晓他们取得的伟大成就对我国乃至世界数学发展起到的巨大推进作用,准备在数学课上随机选取其中一位的成就进行分享,选到数学家刘徽的概率是 .
【考点】概率公式.
【专题】概率及其应用;数据分析观念.
【答案】见试题解答内容
【分析】直接根据概率公式求解即可.
【解答】解:随机选取其中一位的成就进行分享,选到数学家刘徽的概率是,
故答案为:.
【点评】本题主要考查概率公式,随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
15.(2025 凌河区校级三模)如图,一博物馆由圆形主馆A和三个圆形副馆B,C,D组成.一游客从主馆进入,准备参观主馆和一个副馆后离开,已知他随机从副馆四个出口中的一个离开,则他从中间出口(即出口e.f)离开的概率是 .
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】.
【分析】画树状图,共有6种等可能的结果,其中从中间出口(即出口e,f)离开的结果有4种,再由概率公式求解即可.
【解答】解:画树状图如下:
由树状图可知:从中间出口(即出口e,f)离开的结果有4种,
∴他从中间出口(即出口e,f)离开的概率是,
故答案为:.
【点评】本题考查了列表法与树状图法求概率,掌握知识点的应用是解题的关键.
三.解答题(共5小题)
16.(2025 昌邑区校级三模)十二生肖是我国历史悠久的民俗文化符号,是十二地支的形象化代表,根据文献资料记载,最早并广为流传的完整十二生肖循环,是由东汉王充在公元1世纪期间所著《论衡》中提出的.下列三幅十二生肖图片,大小、形状、质地完全相同,将其洗匀,背面朝上放置.
(1)小明从中随机抽取一张,恰好抽到“蛇”的概率是 ;
(2)小丽从中随机抽取一张后并放回,再从中随机抽取一张,请用画树状图(或列表)的方法,求小丽抽取的两张图片恰好是“龙”和“蛇”的概率.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】(1);
(2)见解析,.
【分析】(1)根据题意求解即可;
(2)画树状图可得出所有等可能的结果数以及两张图片恰好是“龙”和“蛇”的结果数,再利用概率公式可得出答案.
【解答】解:(1)小明从中随机抽取一张,恰好抽到“蛇”的概率是,
故答案为:;
(2)根据题意,令三张图片为A,B,C,从中随机抽取一张后并放回,再从中随机抽取一张,作树状图如下:
共有9种等可能的结果,其中小丽抽取的两张图片恰好是“龙”和“蛇”的结果有2种,
∴P(小丽抽取的两张图片恰好是“龙”和“蛇”).
【点评】本题考查列表法与树状图法,概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
17.(2025 永寿县校级模拟)用于观测日出方位和捕捉星辰轨迹的陶寺遗址观象台,是迄今发现的世界最早的天文观测系统,能够精准划分出20个节令,这些节令是传统二十四节气的主要源头.某班语文老师决定从“A.惊蛰,B.清明,C.芒种,D.白露,E.冬至”这五个节气中随机选取主题,布置一次综合实践作业.
(1)若随机选取一个主题,则选中“E.冬至”的概率是 ;
(2)若随机选取两个主题,请利用画树状图或列表的方法,求选取的两个主题是“A.惊蛰,D.白露”的概率.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】(1);
(2).
【分析】(1)根据题意,可以得到随机选取一个主题,则选中“E.冬至”的概率;
(2)根据题意可以画出相应的表格,然后即可得到选取的两个主题是“A.惊蛰,D.白露”的概率.
【解答】解:(1)由题意可得,
随机选取一个主题,则选中“E.冬至”的概率是,
故答案为:;
(2)根据题意,列表如下:
第一个 第二个
A B C D E
A 一 (A,B) (A,C) (A,D) (A,E)
B (B,A) 一 (B,C) (B,D) (B,E)
C (C,A) (C,B) 一 (C,D) (C,E)
D (D,A) (D,B) (D,C) 一 (D,E)
E (E,A) (E,B) (E,C) (E,D) 一
由列表可知,共有20种等可能的结果,其中选取的两个主题是“A.惊蛰,D.白露”的结果有2种,
∴选取的两个主题是“A.惊蛰,D.白露”的概率是.
【点评】本题考查列表法与树状图法、概率公式,解答本题的关键是明确题意,列出相应的表格,求出相应的概率.
18.(2025 青阳县模拟)项目式学习
【项目背景】
为支持乡村振兴,某班级同学在老师的带领下前往某乡开展综合实践活动,其中一个项目是调查该乡农民去年每户的年收入(记为户年收入x),为乡村振兴工作提供参考.
【数据收集与整理】
该乡从几十个村中随机选取四个作为样本供调研,班级同学将这四个村编号为A,B,C,D,经过随机选取恰好选取A,B两村作深层次调研,C,D两村作浅层次调研.在A,B两村中各随机选取了25户农民的户年收入(单位:万元),在C,D两村中各随机选取了10户农民的户年收入(单位:万元),并对数据进行整理,下面给出部分信息:
①A村25户农民的户年收入的频数分布直方图如图(数据分成5组:6≤x<8,8≤x<10,10≤x<12,12≤x<14,14≤x<16);
②A村25户农民的户年收入在10≤x<12这一组的是:10.0,10.0,10.1,10.9,11.4,11.5,11.6,11.8.
③A,B,C,D四个村户年收入的平均数、中位数如下表:
平均数 中位数
A村 10.8 m
B村 11.0 11.5
C村 10.6 未计算
D村 11.2 未计算
任务1从A,B,C,D四个村中随机选取恰好是A,B两村作深层次调研,C,D两村作浅层次调研的概率是 ;
任务2信息③中m的值为 10.1 .
【数据分析与运用】
任务3设从A村随机选取的25户农民的户年收入高于其平均数的个数为f1,从B村随机选取的25户农民的户年收入高于其平均数的个数为f2,比较f1,f2的大小,并说明理由;
任务4请你根据从A,B,C,D四个村随机选取的样本数据,估计该乡2100户农民去年的总收入(单位:万元).
根据所给信息,请完成以上所有任务.
【考点】列表法与树状图法;用样本估计总体;频数(率)分布直方图;加权平均数;中位数.
【答案】任务一:
任务二:10.1;
任务三:f1<f2:
任务四:22890万元.
【分析】任务一:概率计算的关键是明确“所有可能的情况”和“符合条件的情况”,两者的比值即为概率.;
任务二:中位数是将数据按大小排列后,位于中间位置的数值,反映数据的中等水平;
任务三:结合分组数据和中位数的性质分析;
任务四:用样本的平均收入估计总体的平均收入,再乘以总户数得到总体总收入,属于“用样本估计总体”的统计思想.
【解答】解:任务一:从A、B、C、D四个村中选2个作深层次调研,所有可能的组合为:(A,B)、(A,C)、(A,D)、(B,C)、(B,D)、(C,D),共6种等可能情况.
恰好选A、B作深层次调研,C、D作浅层次调研的情况只有1种:(A,B).
概率=符合条件的情况数÷总情况数;
故答案为:;
任务二:A村共25户,中位数是按收入从小到大排列后第13户的收入.
收入 6≤x<8 的有3户,8≤x<10 的有7户,前两组共 3+7=10 户(即第1到10户).
第11到25户在 10≤x<12 及以后区间,其中 10≤x<12 有8户,
因此第13户在 10≤x<12 区间,且是该区间的第 13﹣10=3 户,对应收入为10.1.
所以 m=10.1.
故答案为:10.1;
任务三:A村平均数为10.8,12≤x<14 有4户,14≤x<16 有3户,
这两组合计 4+3=7 户,均大于10.8.
10≤x<12 共8户,其中大于10.8的有 8﹣4=4 户(前4户≤10.8).
因此f1=7+4=11.
B村中位数为11.5,说明第13户收入为11.5(大于11.0),则第13到25户共13户收入均≥11.5,自然大于11.0.
因此 f2≥13.
∴f1<f2.
任务四:样本包含A村25户、B村25户、C村10户、D村10户,
总共有 25+25+10+10=70 户.
样本总收入为:10.8×25+11.0×25+10.6×10+11.2×10=270+275+106+112=763 (万元),
样本平均收入 = 总收入÷总样本数=763÷70=10.9 (万元/户).
该乡共2100户,
总收入≈平均收入×总户数= 10.9×2100=22890 (万元).
答:该乡2100户农民去年的总收入为22890万元.
【点评】本题结合调查农民收入,考查概率问题.
19.(2025 东莞市校级三模)2025年全国两会期间,“体重管理”被纳入国家健康战略.国家卫生健康委员会宣布持续推进为期三年的“体重管理年”行动.为了帮助学生更好地管理体重,广州某初中学校开展了一项体重管理计划,随机抽取了100名学生进行体重指数(BMI)调查.BMI的计算公式为:BMI,根据世界卫生组织的标准,BMI分类如下,调查结果如表所示:
BMI范围 分类
BMI<18.5 体重过轻
18.5≤BMI<24 体重正常
24≤BMI<28 超重
BMI≥28 肥胖
分类 人数
体重过轻 10
体重正常 50
超重 30
肥胖 10
(1)小明身高为1.6m,BMI指数为20,则小明的体重为 51.2 kg;
(2)以下是部分统计图表,请根据表格数据补齐空缺部分.
(3)学校计划从体重正常的2个男生和2个女生中,抽取2名学生介绍体重管理经验,求抽取出来的学生恰好是一男一女的概率.
【考点】列表法与树状图法;扇形统计图;条形统计图;概率公式.
【专题】数据的收集与整理;概率及其应用;数据分析观念;应用意识.
【答案】(1)51.2.
(2)见解答.
(3).
【分析】(1)根据BMI的计算公式代入计算即可.
(2)由表格可知,超重的人数为30人,由扇形统计图可知,超重的百分比为1﹣50%﹣10%﹣10%=30%,补全统计图即可.
(3)列表可得出所有等可能的结果数以及抽取出来的学生恰好是一男一女的结果数,再利用概率公式可得出答案.
【解答】解:(1)∵小明身高为1.6m,BMI指数为20,
∴小明的体重为20×1.62=51.2(kg).
故答案为:51.2.
(2)由表格可知,超重的人数为30人,
扇形统计图中超重的百分比为1﹣50%﹣10%﹣10%=30%.
补全统计图如图所示.
(3)列表如下:
男 男 女 女
男 (男,男) (男,女) (男,女)
男 (男,男) (男,女) (男,女)
女 (女,男) (女,男) (女,女)
女 (女,男) (女,男) (女,女)
共有12种等可能的结果,其中抽取出来的学生恰好是一男一女的结果有8种,
∴抽取出来的学生恰好是一男一女的概率为.
【点评】本题考查列表法与树状图法、条形统计图、扇形统计图、概率公式,能够读懂统计图,掌握列表法与树状图法、概率公式是解答本题的关键.
20.(2025 定西模拟)5月18日是国际博物馆日,为了解甘肃省博物馆的藏品及其承载的历史,弘扬传统文化,小英和小丽准备从博物馆的三个展厅中随机选择一个展厅报名当志愿者,三个展厅如下,分别用A,B,C表示三张形状相同的卡片,其中“A.甘肃佛教艺术展”“B.甘肃古生物化石展”“C.甘肃彩陶展”.现将这3张卡片背面朝上,洗匀放好,小英从中随机抽取一张,记下卡片,放回并洗匀后,小丽再从中随机抽取一张.
(1)小英抽到“A.甘肃佛教艺术展”展厅的概率为 ;
(2)用列表法或画树状图法求出两人恰好抽到“B.甘肃古生物化石展”和“C.甘肃彩陶展”两个展厅的概率.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】(1)
(2)
【分析】(1)直接利用概率公式计算即可;
(2)先列表得到所有结果,找出符合条件的结果利用概率公式计算即可.
【解答】解:(1)∵共有“A.甘肃佛教艺术展”“B.甘肃古生物化石展”“C.甘肃彩陶展”三种等可能的情况,
∴小英从中随机抽取一张,小英抽到“A.甘肃佛教艺术展”展厅的概率为,
故答案为:;
(2)小英从三张形状相同的卡片随机抽取一张,放回并洗匀后,小丽再从中随机抽取一张,列表如下:
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
∴所有的等可能的结果数有9个,两人恰好抽到“B.甘肃古生物化石展”和“C.甘肃彩陶展”两个展厅的结果数有2个,
∴两人恰好抽到“B.甘肃古生物化石展”和“C.甘肃彩陶展”两个展厅的概率为.
【点评】本题主要考查了列表法与树状图法,概率公式,熟练掌握概率的求法是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
