2026年中考数学一轮复习 锐角三角函数(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 锐角三角函数(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2026年中考数学一轮复习 锐角三角函数
一.选择题(共10小题)
1.(2025 港北区三模)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
2.(2025 安庆二模)如图,在正方形网格中,△ABC的位置如图,其中点A、B、C分别在格点上,则tanA的值是( )
A. B. C. D.
3.(2025 旬邑县校级模拟)如图,在△ABC中,∠B=45°,BC=3,,则中线AD的长为( )
A. B.2 C. D.
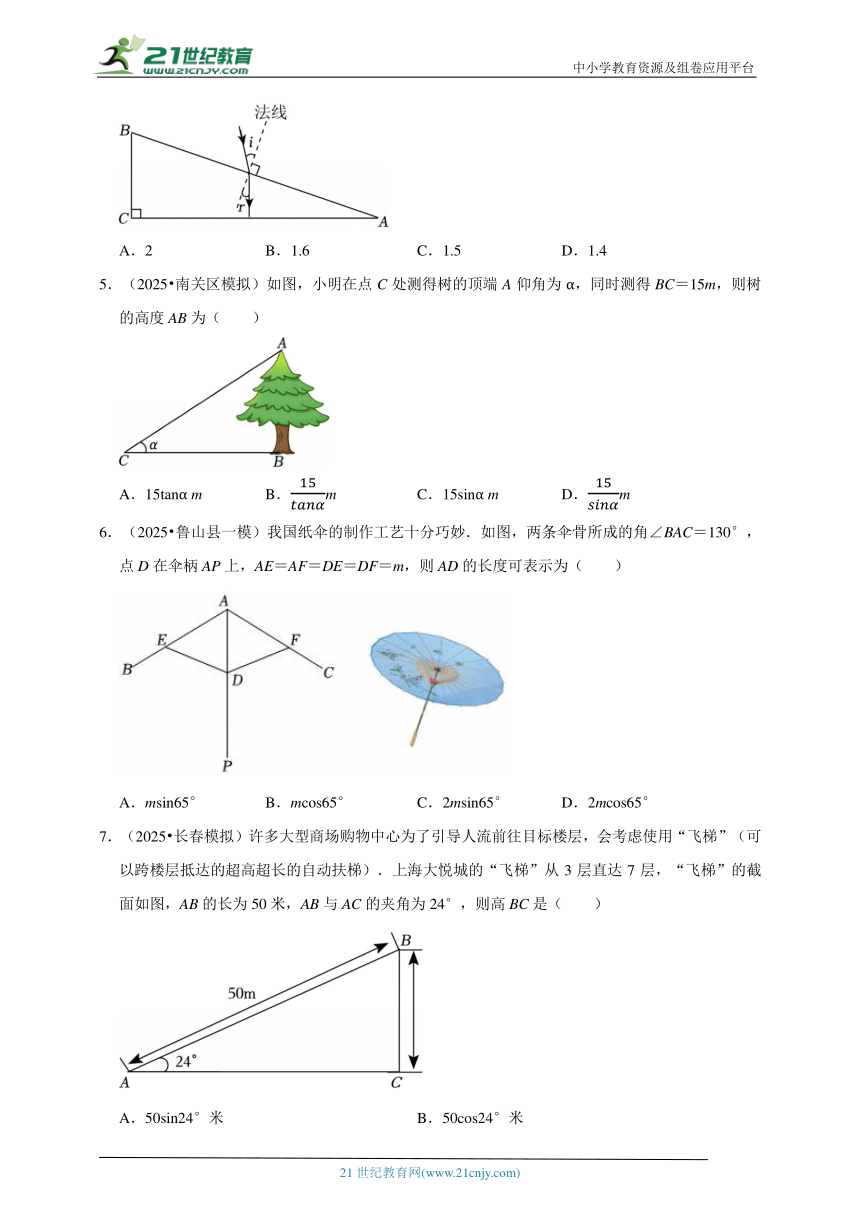
4.(2025 莆田模拟)小媛在物理实验课上研究光的折射现象,了解到当光从空气射入介质时,折射率(i为入射角,r为折射角).如图,一束光从空气射向横截面为直角三角形的硫系玻璃透镜斜面,经折射后沿垂直AC边的方向射出.若i=30°,AB=20cm,BC=5cm,则该玻璃透镜的折射率n为( )
A.2 B.1.6 C.1.5 D.1.4
5.(2025 南关区模拟)如图,小明在点C处测得树的顶端A仰角为α,同时测得BC=15m,则树的高度AB为( )
A.15tanα m B.m C.15sinα m D.m
6.(2025 鲁山县一模)我国纸伞的制作工艺十分巧妙.如图,两条伞骨所成的角∠BAC=130°,点D在伞柄AP上,AE=AF=DE=DF=m,则AD的长度可表示为( )
A.msin65° B.mcos65° C.2msin65° D.2mcos65°
7.(2025 长春模拟)许多大型商场购物中心为了引导人流前往目标楼层,会考虑使用“飞梯”(可以跨楼层抵达的超高超长的自动扶梯).上海大悦城的“飞梯”从3层直达7层,“飞梯”的截面如图,AB的长为50米,AB与AC的夹角为24°,则高BC是( )
A.50sin24°米 B.50cos24°米
C.米 D.米
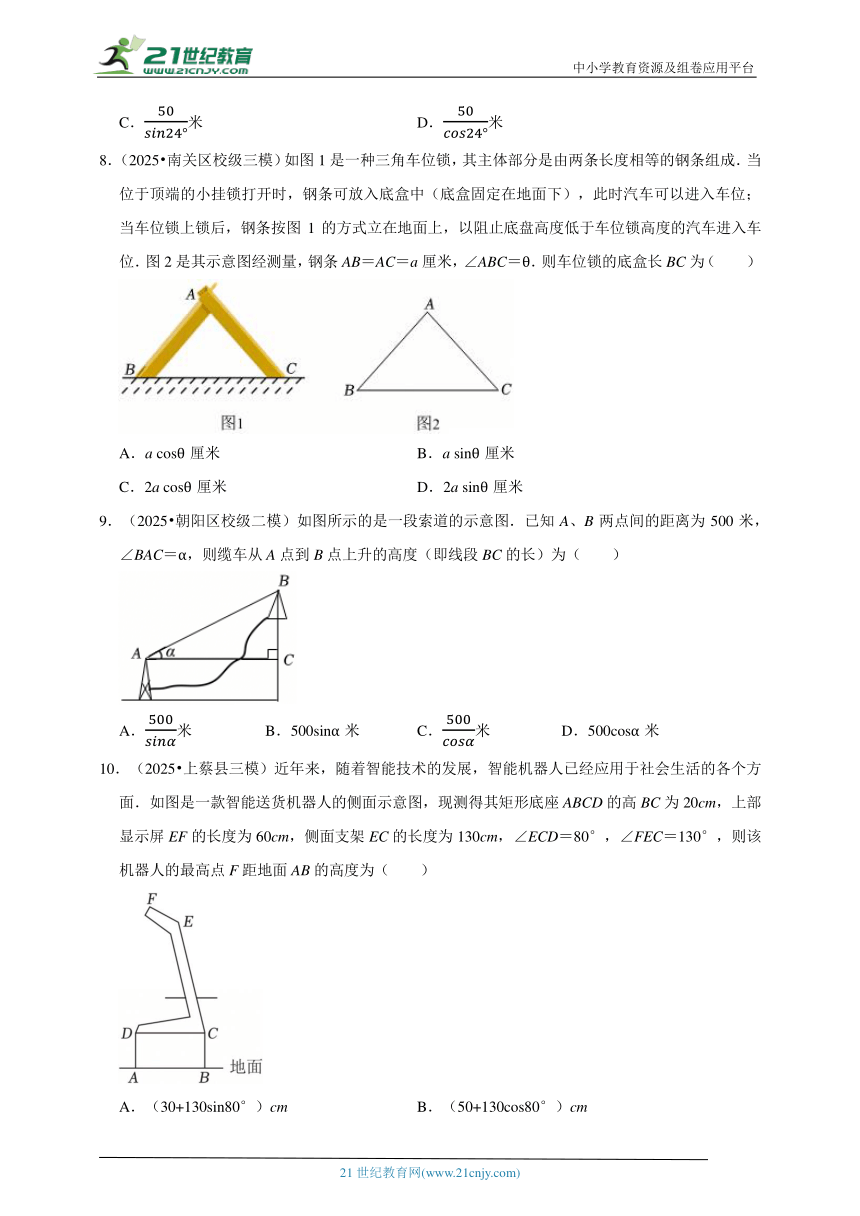
8.(2025 南关区校级三模)如图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图经测量,钢条AB=AC=a厘米,∠ABC=θ.则车位锁的底盒长BC为( )
A.a cosθ厘米 B.a sinθ厘米
C.2a cosθ厘米 D.2a sinθ厘米
9.(2025 朝阳区校级二模)如图所示的是一段索道的示意图.已知A、B两点间的距离为500米,∠BAC=α,则缆车从A点到B点上升的高度(即线段BC的长)为( )
A.米 B.500sinα米 C.米 D.500cosα米
10.(2025 上蔡县三模)近年来,随着智能技术的发展,智能机器人已经应用于社会生活的各个方面.如图是一款智能送货机器人的侧面示意图,现测得其矩形底座ABCD的高BC为20cm,上部显示屏EF的长度为60cm,侧面支架EC的长度为130cm,∠ECD=80°,∠FEC=130°,则该机器人的最高点F距地面AB的高度为( )
A.(30+130sin80°)cm B.(50+130cos80°)cm
C. D.(50+130sin80°)cm
二.填空题(共5小题)
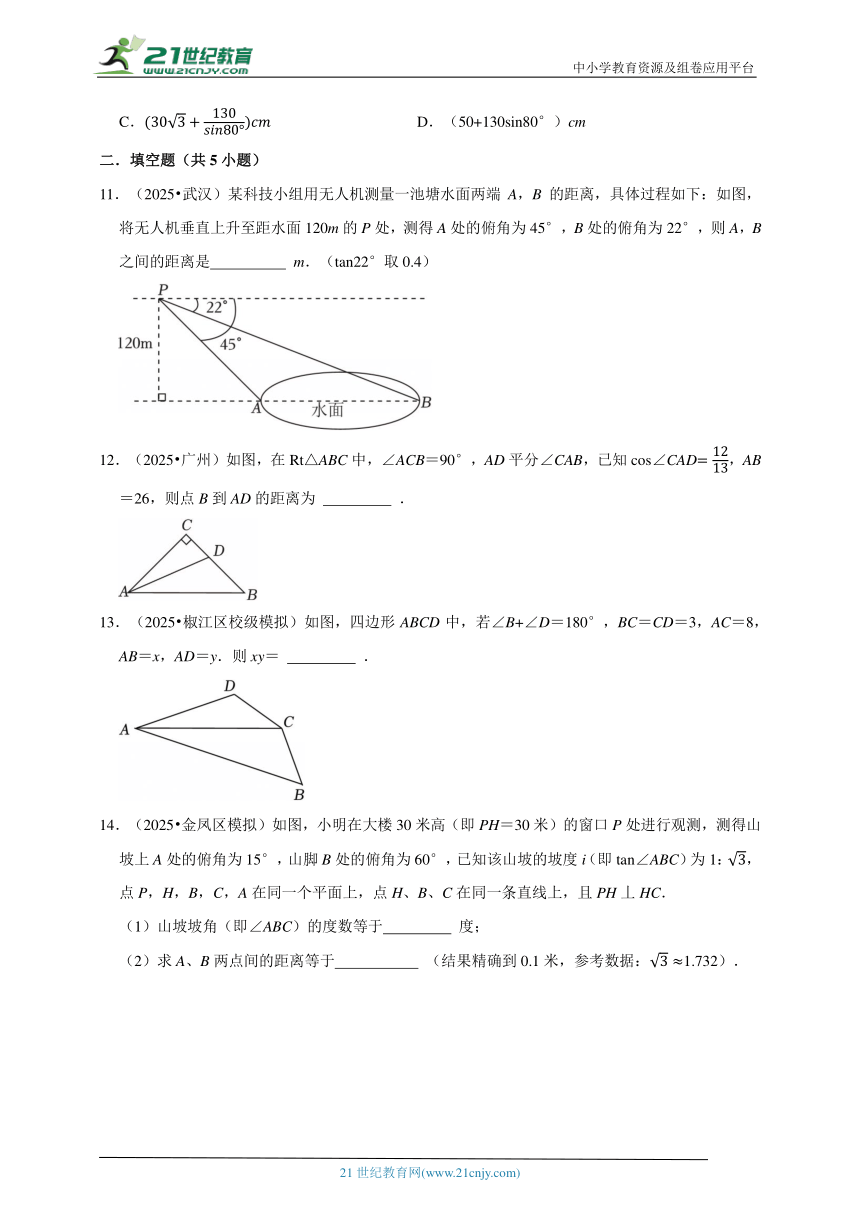
11.(2025 武汉)某科技小组用无人机测量一池塘水面两端A,B的距离,具体过程如下:如图,将无人机垂直上升至距水面120m的P处,测得A处的俯角为45°,B处的俯角为22°,则A,B之间的距离是 m.(tan22°取0.4)
12.(2025 广州)如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,已知cos∠CAD,AB=26,则点B到AD的距离为 .
13.(2025 椒江区校级模拟)如图,四边形ABCD中,若∠B+∠D=180°,BC=CD=3,AC=8,AB=x,AD=y.则xy= .
14.(2025 金凤区模拟)如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求A、B两点间的距离等于 (结果精确到0.1米,参考数据:1.732).
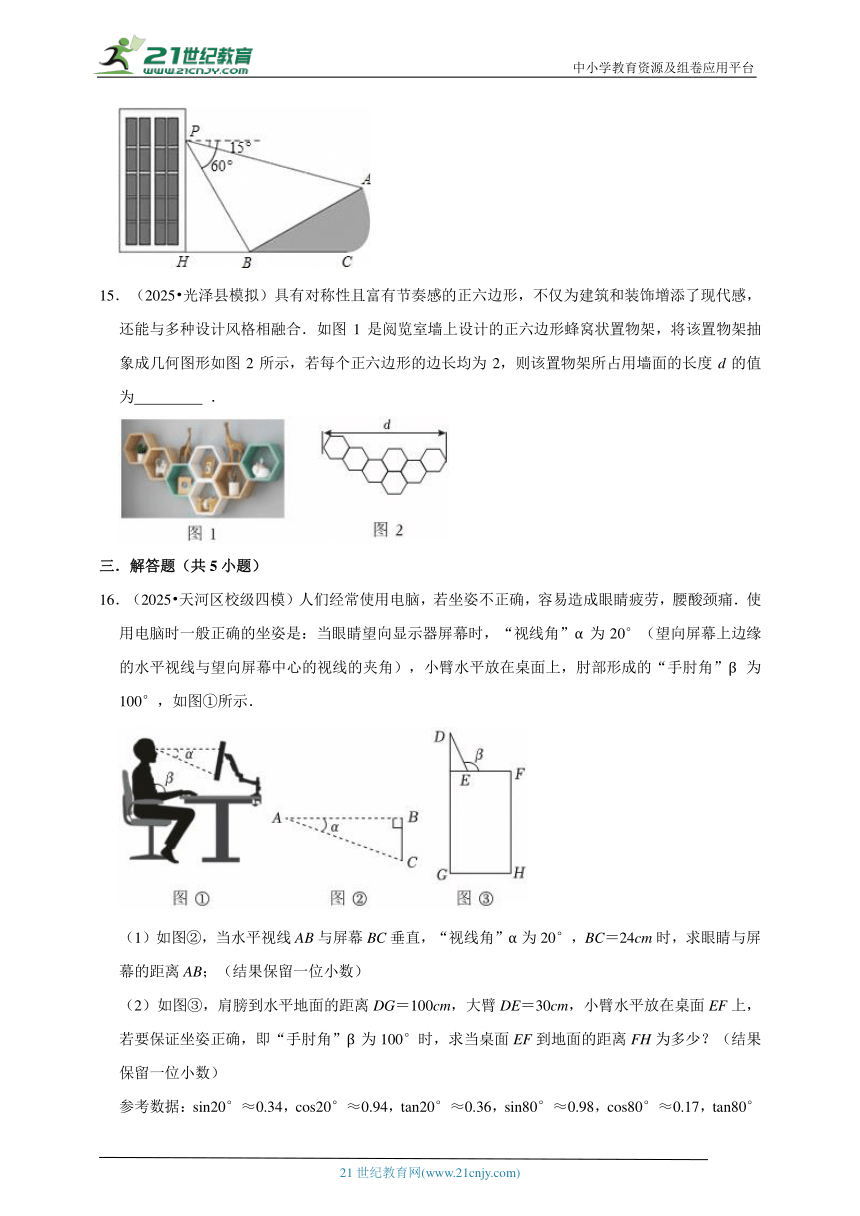
15.(2025 光泽县模拟)具有对称性且富有节奏感的正六边形,不仅为建筑和装饰增添了现代感,还能与多种设计风格相融合.如图1是阅览室墙上设计的正六边形蜂窝状置物架,将该置物架抽象成几何图形如图2所示,若每个正六边形的边长均为2,则该置物架所占用墙面的长度d的值为 .
三.解答题(共5小题)
16.(2025 天河区校级四模)人们经常使用电脑,若坐姿不正确,容易造成眼睛疲劳,腰酸颈痛.使用电脑时一般正确的坐姿是:当眼睛望向显示器屏幕时,“视线角”α为20°(望向屏幕上边缘的水平视线与望向屏幕中心的视线的夹角),小臂水平放在桌面上,肘部形成的“手肘角”β为100°,如图①所示.
(1)如图②,当水平视线AB与屏幕BC垂直,“视线角”α为20°,BC=24cm时,求眼睛与屏幕的距离AB;(结果保留一位小数)
(2)如图③,肩膀到水平地面的距离DG=100cm,大臂DE=30cm,小臂水平放在桌面EF上,若要保证坐姿正确,即“手肘角”β为100°时,求当桌面EF到地面的距离FH为多少?(结果保留一位小数)
参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin80°≈0.98,cos80°≈0.17,tan80°≈5.67
17.(2025 永寿县校级模拟)“生命之树”(如图①)是以西安古观音禅寺的千年银杏树为原型,用建筑和自然结合的方式打造的城市特色建筑景观.如图②,由于“生命之树”主体底部不可直接测量,小兴计划利用无人机测量该“生命之树”主体的高度,他先用无人机从地面上的点D处竖直上升100m到达点C处,在点C处测得“生命之树”主体AB的顶点A处的俯角为22°,然后操控无人机向主体AB的方向水平飞行65m至点E处,在点E处测得顶点A处的俯角为45°,点B,D在同一水平线上,AB⊥BD,图中所有点均在同一平面内,求“生命之树”主体AB的高度.(结果保留整数,参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
18.(2025 广东模拟)图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1m,主臂MP长为5m,测得主臂伸展角.∠PME=37°.(参考数据:sin37°,tan37°,sin53°,tan53°)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q,此时∠QPM=90°,求Q点到N点的距离.
19.(2025 武安市二模)淇淇家位于学校正东方向200m处,周末她和同学约好去学校附近的体育馆打篮球,已知体育馆位于学校北偏西53°方向,距离学校500m.
(1)请根据描述画出淇淇家、学校和体育馆的方位示意图;
(2)求体育馆到淇淇家的直线距离;
(3)若淇淇步行从家出发,先以50m/min的速度匀速走到学校,但到达学校后,发现忘带篮球,于是立即以60m/min的速度原路返回家中.取到篮球后,为了赶时间,她以80m/min的速度从家直接走到体育馆,求淇淇全程所用的时长.(计算结果保留整数.参考数据:sin53°=0.8,
20.(2025 凌河区校级三模)如图1,某款线上教学设备由底座、支撑臂AB、连杆BC、悬臂CD和安装在D处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图.已知支撑臂AB⊥l,AB=18cm,CD=44cm,固定∠ABC=148°,可通过调试悬臂CD与连杆BC的夹角来提高拍摄效果.悬臂端点C到桌面l的距离约为52cm.
(1)BC的长度为多少?
(2)已知摄像头点D到桌面l的距离为30cm时拍摄效果较好,那么此时悬臂CD与连杆BC的夹角∠BCD的度数约为多少?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
2026年中考数学一轮复习 锐角三角函数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 港北区三模)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】C
【分析】根据题意结合图形可知β是重力G与斜面形成的三角形的外角,从而可求得β的度数.
【解答】解:∵重力G的方向竖直向下,
∴重力G与水平方向夹角为90°,
由题意可得:
∴β=∠1=α+90°=115°,
故选:C.
【点评】本题考查了平行线的性质和三角形外角性质,正确进行计算是解题关键.
2.(2025 安庆二模)如图,在正方形网格中,△ABC的位置如图,其中点A、B、C分别在格点上,则tanA的值是( )
A. B. C. D.
【考点】解直角三角形.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】取格点D,连接CD,设每个小正方形的边长为1,由勾股定理结合勾股定理逆定理可得△ACD为直角三角形,且∠ADC=90°,再由正切的定义计算即可得解.
【解答】解:如图所示:取格点D,连接CD,
设每个小正方形的边长为1,由勾股定理可得:
,,,
∴AC2=AD2+CD2,
∴△ACD为Rt△,且∠ADC=90°,
∴tanA,
故选:B.
【点评】本题考查了勾股定理、勾股定理逆定理、求角的正切值,熟练掌握以上知识点是关键.
3.(2025 旬邑县校级模拟)如图,在△ABC中,∠B=45°,BC=3,,则中线AD的长为( )
A. B.2 C. D.
【考点】解直角三角形.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】过点A作AE⊥BC于点E,设AE=x,分别在Rt△ABE和Rt△AEC中,利用锐角三角函数的定义求出BE和CE的长,从而列出关于x的方程,进而求出BC的长,再利用三角形的中线定义求出BD的长,从而求出DE的长,最后在Rt△ADE中,利用勾股定理进行计算即可解答.
【解答】解:过点A作AE⊥BC于点E,
设AE=x,
在Rt△ABE中,∠B=45°,
∴BE=AE tan45°=x,
在Rt△AEC中,tanC
∴,
∴CE=2AE=2x,
∴BC=BE+CE,
∴x+2x=3,
解得:x=1,
∴AE=BE=1,
∵AD是BC边上的中线,
∴BD=CDBC=1.5,
∴DE=BD﹣BE=1.5﹣1=0.5,
在Rt△ADE中,
故选:D.
【点评】本题考查了解直角三角形,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
4.(2025 莆田模拟)小媛在物理实验课上研究光的折射现象,了解到当光从空气射入介质时,折射率(i为入射角,r为折射角).如图,一束光从空气射向横截面为直角三角形的硫系玻璃透镜斜面,经折射后沿垂直AC边的方向射出.若i=30°,AB=20cm,BC=5cm,则该玻璃透镜的折射率n为( )
A.2 B.1.6 C.1.5 D.1.4
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用.
【答案】A
【分析】由题意得β+∠A=90°,r+β=90°,则r=∠A,所以,然后通过折射率即可求解.
【解答】解:如图,
∵折射光线沿垂直AC边的方向射出β+∠A=90°,
∵法线垂直于AB,
∴r+β=90°,
∴r=∠A,
∴,
∵折射率,
故选:A.
【点评】本题考查了解直角三角形的应用,同角的余角相等,掌握知识点的应用是解题的关键.
5.(2025 南关区模拟)如图,小明在点C处测得树的顶端A仰角为α,同时测得BC=15m,则树的高度AB为( )
A.15tanα m B.m C.15sinα m D.m
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】A
【分析】由锐角三角函数定义得tanα,即可得出答案.
【解答】解:在Rt△ABC中,BC=15m,∠ACB=α,tanα,
∴AB=BC tanα=15tanα(m).
故选:A.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题及坡度坡角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
6.(2025 鲁山县一模)我国纸伞的制作工艺十分巧妙.如图,两条伞骨所成的角∠BAC=130°,点D在伞柄AP上,AE=AF=DE=DF=m,则AD的长度可表示为( )
A.msin65° B.mcos65° C.2msin65° D.2mcos65°
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】连接EF交AD于点O,根据已知易得:四边形AEDF是菱形,从而利用菱形的性质可得OA=ODAD,∠AOF=90°,∠FAD=65°,然后在Rt△AOF中,利用锐角三角函数的定义求出AO的长,从而求出AD的长,即可解答.
【解答】解:连接EF交AD于点O,
∵AE=AF=DE=DF=m,
∴四边形AEDF是菱形,
∴OA=ODAD,∠AOF=90°,∠FAD∠EAF=65°,
在Rt△AOF中,AO=AF cos65°=mcos65°,
∴AD=2AO=2mcos65°,
∴AD的长度可表示为2mcos65°,
故选:D.
【点评】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
7.(2025 长春模拟)许多大型商场购物中心为了引导人流前往目标楼层,会考虑使用“飞梯”(可以跨楼层抵达的超高超长的自动扶梯).上海大悦城的“飞梯”从3层直达7层,“飞梯”的截面如图,AB的长为50米,AB与AC的夹角为24°,则高BC是( )
A.50sin24°米 B.50cos24°米
C.米 D.米
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;几何直观;运算能力.
【答案】A
【分析】根据图形和锐角三角函数,可以表示出BC的值.
【解答】解:∵∠BCA=90°,AB=50m,∠A=24°,
∴sinA,
∴BC=50sinA=50sin24°(米),
故选:A.
【点评】本题考查解直角三角形的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
8.(2025 南关区校级三模)如图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图经测量,钢条AB=AC=a厘米,∠ABC=θ.则车位锁的底盒长BC为( )
A.a cosθ厘米 B.a sinθ厘米
C.2a cosθ厘米 D.2a sinθ厘米
【考点】解直角三角形的应用;等腰三角形的性质.
【专题】解直角三角形及其应用;运算能力.
【答案】C
【分析】根据题意,结合图形,在Rt△ADB中利用三角函数得到BD,结合等腰三角形的性质得到结果.
【解答】解:过A点作AD⊥BC于D点,
∵AB=AC,△ABC是等腰三角形,
∴BD=DC,
∵在Rt△ADB中,∠ADB=90°,∠ABD=θ,AB=a厘米,
∴BD=AB cos∠ABD=a cosθ(厘米),
∴BC=2a cosθ(厘米),
故选:C.
【点评】本题考查了解直角三角形的应用,熟练掌握解直角三角形是解题的关键.
9.(2025 朝阳区校级二模)如图所示的是一段索道的示意图.已知A、B两点间的距离为500米,∠BAC=α,则缆车从A点到B点上升的高度(即线段BC的长)为( )
A.米 B.500sinα米 C.米 D.500cosα米
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】根据题意可得:BC⊥AC,然后在Rt△ABC中,利用锐角三角函数的定义求出BC的长,即可解答.
【解答】解:由题意得:BC⊥AC,
在Rt△ABC中,∠BAC=α,AB=500米,
∴BC=AB sinα=500sinα(米),
∴缆车从A点到B点上升的高度为500sinα米,
故选:B.
【点评】本题考查了解直角三角形的应用,准确熟练地进行计算是解题的关键.
10.(2025 上蔡县三模)近年来,随着智能技术的发展,智能机器人已经应用于社会生活的各个方面.如图是一款智能送货机器人的侧面示意图,现测得其矩形底座ABCD的高BC为20cm,上部显示屏EF的长度为60cm,侧面支架EC的长度为130cm,∠ECD=80°,∠FEC=130°,则该机器人的最高点F距地面AB的高度为( )
A.(30+130sin80°)cm B.(50+130cos80°)cm
C. D.(50+130sin80°)cm
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】过点E,F分别作EH⊥CD,FN⊥CD,垂足分别为H,N,过点E作EM⊥FN,垂足为M,可得四边形EMNH为矩形,即得MN=EH,再分别解Rt△EHC和Rt△FEM,求出EH、FM即可求解.
【解答】解:过点E,F分别作EH⊥CD,FN⊥CD,垂足分别为H,N,过点E作EM⊥FN,垂足为M,则四边形EMNH为矩形,
∴MN=EH,
∵,
∴EH=CE sin∠ECH=130sin80°(cm),
∴MN=130sin80°(cm),
∵∠EHC=90°,
∴∠CEH=90°﹣80°=10°,
∴∠FEM=∠FEC﹣∠MEH﹣∠CEH=130°﹣90°﹣10°=30°,
∴,
∴点F距地面AB的高度为FM+MN+BC=30+130sin80°+20=(50+130sin80°)cm,
故选:D.
【点评】本题考查了解直角三角形的应用,矩形的判定和性质,正确进行计算是解题关键.
二.填空题(共5小题)
11.(2025 武汉)某科技小组用无人机测量一池塘水面两端A,B的距离,具体过程如下:如图,将无人机垂直上升至距水面120m的P处,测得A处的俯角为45°,B处的俯角为22°,则A,B之间的距离是 180 m.(tan22°取0.4)
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】180.
【分析】根据题意可得:PD∥CB,从而可得∠PAC=∠DPA=45°,∠DPB=∠PBC=22°,然后分别在Rt△PAC和Rt△PBC中,利用锐角三角函数的定义求出AC和BC的长,从而进行计算即可解答.
【解答】解:如图:
由题意得:PD∥CB,
∴∠PAC=∠DPA=45°,∠DPB=∠PBC=22°,
在Rt△PAC中,PC=120m,
∴AC120(m),
在Rt△PBC中,∠PBC=22°,
∴BC300(m),
∴AB=BC﹣AC=300﹣120=180(m),
∴A,B之间的距离约是180m,
故答案为:180.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,根据题目的已知条件并结合图形进行分析添加适当的辅助线是解题的关键.
12.(2025 广州)如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,已知cos∠CAD,AB=26,则点B到AD的距离为 10 .
【考点】解直角三角形;角平分线的性质.
【专题】解直角三角形及其应用;运算能力.
【答案】10.
【分析】过点D作DH⊥AB于点H.可以假设AC=12k,AD=13k,则CD=5k,证明DH=CD=5k,利用面积法求解.
【解答】解:过点D作DH⊥AB于点H.
∵∠C=90°,cos∠CAD,
∴可以假设AC=12k,AD=13k,则CD=5k,
∵AD平分∠CAB,DC⊥AC,DH⊥AB,
∴DH=DC=5k,
设点B到AD的距离为h,则有13k×h26×5k,
解得h=10.
故答案为:10.
【点评】本题考查解直角三角形,角平分线的性质,解题的关键是学会利用参数构建方程解决问题.
13.(2025 椒江区校级模拟)如图,四边形ABCD中,若∠B+∠D=180°,BC=CD=3,AC=8,AB=x,AD=y.则xy= 55 .
【考点】解直角三角形.
【专题】三角形;解直角三角形及其应用;几何直观;运算能力;推理能力.
【答案】55.
【分析】过点C作CE⊥AB于点E,CF⊥AD,交AD延长线于点F,证明∠B=∠CDF=α,解Rt△BCE得CE=3sinα,BE=3cosα,则AE=x﹣3cosα,由勾股定理得AE2+CE2=AC2,则(x﹣3cosα)2+(3sinα)2=82,整理得x2﹣6xcosα=55①,解Rt△CDF得CF=3sinα,DF=3cosα,则AF=y+3cosα,由勾股定理得AF2+CF2=AC2,则(y+3cosα)2+(3sinα)2=82,整理得y2+6ycosα=55②,由①②得x2﹣6xcosα=y2+6ycosα,由此得x﹣y=6cosα,则x2+y2﹣2xy=36cos2α,再由①+②得x2+y2=110+36cos2α,进而得110+36cos2α﹣2xy=36cos2α,由此即可得出xy的值.
【解答】解:过点C作CE⊥AB于点E,CF⊥AD,交AD的延长线于点F,如图所示:
∵∠B+∠ADC=180°,∠CDF+∠ADC=180°,
∴∠B=∠CDF,
设∠B=∠CDF=α,
在Rt△BCE中,∠B=α,BC=3,
∴sinα,cosα,
∴CE=BC sinα=3sinα,BE=BC cosα=3cosα,
∵AB=x,
∴AE=AB﹣BE=x﹣3cosα,
在Rt△ACE中,AC=8,
由勾股定理得:AE2+CE2=AC2,
∴(x﹣3cosα)2+(3sinα)2=82,
整理得:x2﹣6xcosα+9(sin2α+cos2α)=64,
∵sin2α+cos2α=1,
∴x2﹣6xcosα=55①,
在Rt△CDF中,∠CDF=α,CD=3,
∴sinα,cosα,
∴CF=CD sinα=3sinα,DF=CD cosα=3cosα,
∵AD=y,
∴AF=AD+DF=y+3cosα,
在Rt△ACF中,AC=8,
由勾股定理得:AF2+CF2=AC2,
∴(y+3cosα)2+(3sinα)2=82,
整理得:y2+6ycosα+9(sin2α+cos2α)=64,
∵sin2α+cos2α=1,
∴y2+6ycosα=55②,
由①②得:x2﹣6xcosα=y2+6ycosα,
∴(x+y)(x﹣y)=6(x+y)cosα,
∵x+y≠0,
∴x﹣y=6cosα,
∴(x﹣y)2=(6cosα)2,
∴x2+y2﹣2xy=36cos2α,
由①+②得:x2﹣6xcosα+y2+6ycosα=110,
∴x2+y2=110+6(x﹣y)cosα=110+6×6cosα×cosα,
∴x2+y2=110+36cos2α,
∴110+36cos2α﹣2xy=36cos2α,
∴xy=55.
故答案为:55.
【点评】此题主要考查了解直角三角形,熟练掌握锐角三角函数的定义,勾股定理,完全平方公式的结构特征是解决问题的关键.
14.(2025 金凤区模拟)如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
(1)山坡坡角(即∠ABC)的度数等于 30 度;
(2)求A、B两点间的距离等于 34.6 (结果精确到0.1米,参考数据:1.732).
【考点】解直角三角形的应用﹣仰角俯角问题.
【答案】见试题解答内容
【分析】(1)根据俯角以及坡度的定义即可求解;
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
【解答】解:(1)∵tan∠ABC=1:,
∴∠ABC=30°;
(2)由题意得:∠PBH=60°,
∵∠ABC=30°,
∴∠ABP=90°,又∠APB=45°,
∴△PAB为等腰直角三角形,
在直角△PHB中,PB20.
在直角△PBA中,AB=PB=2034.6米.
故答案为30,34.6.
【点评】本题主要考查了俯角的问题以及坡度的定义,正确利用三角函数是解题的关键.
15.(2025 光泽县模拟)具有对称性且富有节奏感的正六边形,不仅为建筑和装饰增添了现代感,还能与多种设计风格相融合.如图1是阅览室墙上设计的正六边形蜂窝状置物架,将该置物架抽象成几何图形如图2所示,若每个正六边形的边长均为2,则该置物架所占用墙面的长度d的值为 19 .
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】19.
【分析】根据题意可得:点A,B,C,D,E,F,G,H共线,连接AB并延长到点H,则AH⊥HM,根据题意可得:AB=CD=EF=4,BC=DE=FG=GM=2,然后在Rt△GHM中,利用锐角三角函数的定义求出GH的长,最后进行计算即可解答.
【解答】解:如图:由题意得:点A,B,C,D,E,F,G,H共线,连接AB并延长到点H,则AH⊥HM,
由题意得:AB=CD=EF=4,BC=DE=FG=GM=2,
在Rt△GHM中,∠MGH=60°,
∴GH=GM cos60°=21,
∴AH=AB+BC+CD+DE+EF+FG+GH=4+2+4+2+4+2+1=19,
∴该置物架所占用墙面的长度d的值为19,
故答案为:19.
【点评】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添适当的辅助线是解题的关键.
三.解答题(共5小题)
16.(2025 天河区校级四模)人们经常使用电脑,若坐姿不正确,容易造成眼睛疲劳,腰酸颈痛.使用电脑时一般正确的坐姿是:当眼睛望向显示器屏幕时,“视线角”α为20°(望向屏幕上边缘的水平视线与望向屏幕中心的视线的夹角),小臂水平放在桌面上,肘部形成的“手肘角”β为100°,如图①所示.
(1)如图②,当水平视线AB与屏幕BC垂直,“视线角”α为20°,BC=24cm时,求眼睛与屏幕的距离AB;(结果保留一位小数)
(2)如图③,肩膀到水平地面的距离DG=100cm,大臂DE=30cm,小臂水平放在桌面EF上,若要保证坐姿正确,即“手肘角”β为100°时,求当桌面EF到地面的距离FH为多少?(结果保留一位小数)
参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin80°≈0.98,cos80°≈0.17,tan80°≈5.67
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;应用意识.
【答案】(1)眼睛与屏幕的距离AB约为66.7cm;
(2)桌面EF到地面的距离FH约为70.6cm.
【分析】(1)根据BC的长及20°的正切值可得AB的长;
(2)易得∠DEM=80°,根据DE的长和80°的正弦值可得MG的长,取DG的长,减去MG的长即为桌面EF到地面的距离.
【解答】解:(1)∵AB⊥BC,
∴∠B=90°,
∵α=20°,BC=24cm,
∴AB66.7(cm),
答:眼睛与屏幕的距离AB约为66.7cm;
(2)由题意得:四边形GMFH是矩形,∠DME=90°,
∵β=100°,
∴∠DEM=80°,
∵DE=30cm,
∴DM=DE sin80°≈30×0.98≈29.4(cm),
∵DG=100cm,
∴GM=100﹣29.4=70.6(cm),
∴FH=GM=70.6cm.
答:桌面EF到地面的距离FH约为70.6cm.
【点评】本题考查解直角三角形的应用.掌握锐角三角函数的性质是解决本题的关键.
17.(2025 永寿县校级模拟)“生命之树”(如图①)是以西安古观音禅寺的千年银杏树为原型,用建筑和自然结合的方式打造的城市特色建筑景观.如图②,由于“生命之树”主体底部不可直接测量,小兴计划利用无人机测量该“生命之树”主体的高度,他先用无人机从地面上的点D处竖直上升100m到达点C处,在点C处测得“生命之树”主体AB的顶点A处的俯角为22°,然后操控无人机向主体AB的方向水平飞行65m至点E处,在点E处测得顶点A处的俯角为45°,点B,D在同一水平线上,AB⊥BD,图中所有点均在同一平面内,求“生命之树”主体AB的高度.(结果保留整数,参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】“生命之树”主体AB的高度约为57m.
【分析】如图,过点A作 AF⊥CE,交CE的延长线于点F,根据矩形的性质得到BF=CD=100m,由题意知∠ACF=22°,∠AEF=45°,CE=65m,求得EF=AF,设EF=AF=x m,则CF=CE+EF=(65+x)m,解直角三角形即可得到结论.
【解答】解:如图,过点A作 AF⊥CE,交CE的延长线于点F,
∵点B,D在同一水平线上,AB⊥BD,
∴四边形CDBF为矩形,
∴BF=CD=100m,
由题意知∠ACF=22°,∠AEF=45°,CE=65m,
∴EF=AF,
设EF=AF=x m,则CF=CE+EF=(65+x)m,
在Rt△ACF中,,
∴,
解得x≈43.3,
∴AF=43.3m,
∴AB=100﹣43.3=56.7=57(m),
答:“生命之树”主体AB的高度约为57m.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,正确地作出辅助线是解题的关键.
18.(2025 广东模拟)图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1m,主臂MP长为5m,测得主臂伸展角.∠PME=37°.(参考数据:sin37°,tan37°,sin53°,tan53°)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q,此时∠QPM=90°,求Q点到N点的距离.
【考点】解直角三角形的应用.
【专题】计算题;数形结合;解直角三角形及其应用;运算能力;应用意识.
【答案】(1)点P到地面的高度约为4m;
(2)Q点到N点的距离约为7m.
【分析】(1)作PB⊥QN于点B,延长ME交PB于点A.易得四边形ABNM是矩形,那么AB=MN,AM=BN,根据37°的正弦值和PM的长可得PA的长,加上AB的长即为点P到地面的高度;
(2)根据勾股定理可得AM的长,也就是BN的长,根据∠QPM=90°,可得∠QPB=37°,根据37°的正切值和PB的长可得QB的长,加上BN的长即为Q点到N点的距离.
【解答】解:(1)作PB⊥QN于点B,延长ME交PB于点A.
∴∠PBQ=∠PBN=90°.
∵EM∥QN,
∴∠BAE=∠PAE=90°.
由题意得:MN⊥BN,
∴∠MNB=90°.
∴四边形ABNM是矩形.
∴AB=MN=1(m),AM=BN.
∵PM=5m,∠PME=37°,
∴PA=PM sin∠PME≈53(m).
∴PB=PA+AB=3+1=4(m).
答:点P到地面的高度约为4m;
(2)∵PA=3m,PM=5m,∠PAM=90°,
∴AM=4(m),∠APM+∠PME=90°.
∴BN=4(m).
∵∠QPM=90°,
∴∠QPB+∠APM=90°.
∴∠QPB=∠PME=37°.
∴QB=PB tan∠QPB≈43(m).
∴QN=QB+BN=7(m).
答:Q点到N点的距离约为7m.
【点评】本题考查解直角三角形的应用.把所给的线段和角整理到合适的直角三角形中是解决本题的关键.
19.(2025 武安市二模)淇淇家位于学校正东方向200m处,周末她和同学约好去学校附近的体育馆打篮球,已知体育馆位于学校北偏西53°方向,距离学校500m.
(1)请根据描述画出淇淇家、学校和体育馆的方位示意图;
(2)求体育馆到淇淇家的直线距离;
(3)若淇淇步行从家出发,先以50m/min的速度匀速走到学校,但到达学校后,发现忘带篮球,于是立即以60m/min的速度原路返回家中.取到篮球后,为了赶时间,她以80m/min的速度从家直接走到体育馆,求淇淇全程所用的时长.(计算结果保留整数.参考数据:sin53°=0.8,
【考点】解直角三角形的应用﹣方向角问题;作图—应用与设计作图.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)方位示意图见解析部分;
(2)体育馆到淇淇家的直线距离约为660米;
(3)淇淇全程所用的时长为15.6min.
【分析】(1)根据题意,画出方位示意图即可;
(2)结合图形,在Rt△ACD中求出AD,CD,在Rt△BCD中利用勾股定理即可求出BC;
(3)根据题意,分别计算出淇淇每段路程所用的时间,即可得到总用时.
【解答】解:(1)淇淇家、学校和体育馆的方位示意图如图1所示,
(2)如图2,过C点作CD⊥AB,并BA的延长线于点D,
依题意,∠DCA=53°,AB=200米,AC=500米,
∴在Rt△ACD中,AD=AC sin∠DCA=500×sin53°≈400(米),
CD=AC cos∠DCA=500×cos53°≈300(米),
∴BD=AD+AB=400+200=600(米),
∵在Rt△BCD中,BC2=BD2+CD2=6002+3002=450000,
∴BC=300660(米),
答:体育馆到淇淇家的直线距离约为660米;
(3)∵淇淇从家出发以50m/min的速度匀速走到学校,
∴所用时间为200÷50=4(min),
∵以60m/min的速度原路返回家中,
∴所用时间为200÷60(min),
∵以80m/min的速度从家直接走到体育馆,
∴所用时间为660÷80=8.25(min),
∴淇淇全程所用的时长为48.25≈15.6(min),
答:淇淇全程所用的时长为15.6min.
【点评】本题考查了解直角三角形的应用,熟练掌握解直角三角形是解题的关键.
20.(2025 凌河区校级三模)如图1,某款线上教学设备由底座、支撑臂AB、连杆BC、悬臂CD和安装在D处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图.已知支撑臂AB⊥l,AB=18cm,CD=44cm,固定∠ABC=148°,可通过调试悬臂CD与连杆BC的夹角来提高拍摄效果.悬臂端点C到桌面l的距离约为52cm.
(1)BC的长度为多少?
(2)已知摄像头点D到桌面l的距离为30cm时拍摄效果较好,那么此时悬臂CD与连杆BC的夹角∠BCD的度数约为多少?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)BC的长度约为40cm;
(2)此时悬臂CD与连杆BC的夹角∠BCD的度数约为28°.
【分析】(1)过点C作CE⊥l,垂足为E,过点B作BF⊥CE,垂足为F,根据题意可得:∠ABF=90°,AB=EF=18cm,CE=52cm,从而可得CF=34cm,∠CBF=58°,然后在Rt△CBF中,利用锐角三角函数的定义进行计算即可解答;
(2)过点D作DG⊥CE,垂足为G,根据题意可得:EG=30cm,AB∥CE,从而可得∠BCE=32°,CG=22cm,然后在Rt△CDG中,利用锐角三角函数的定义可得cos∠DCG,从而可得∠DCG=60°,最后利用角的和差关系进行计算即可解答.
【解答】解:(1)过点C作CE⊥l,垂足为E,过点B作BF⊥CE,垂足为F,
由题意得:∠ABF=90°,AB=EF=18cm,CE=52cm,
∴CF=CE﹣EF=34(cm),
∵∠ABC=148°,
∴∠CBF=∠ABC﹣∠ABF=58°,
在Rt△CBF中,BC40(cm),
∴BC的长度约为40cm;
(2)过点D作DG⊥CE,垂足为G,
由题意得:EG=30cm,AB∥CE,
∴∠BCE=180°﹣∠ABC=32°,
∵CE=52cm,
∴CG=CE﹣EG=52﹣30=22(cm),
在Rt△CDG中,CD=44cm,
∴cos∠DCG,
∴∠DCG=60°,
∴∠DCB=∠DCG﹣∠BCE=28°,
∴此时悬臂CD与连杆BC的夹角∠BCD的度数约为28°.
【点评】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年中考数学一轮复习 锐角三角函数
一.选择题(共10小题)
1.(2025 港北区三模)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
2.(2025 安庆二模)如图,在正方形网格中,△ABC的位置如图,其中点A、B、C分别在格点上,则tanA的值是( )
A. B. C. D.
3.(2025 旬邑县校级模拟)如图,在△ABC中,∠B=45°,BC=3,,则中线AD的长为( )
A. B.2 C. D.
4.(2025 莆田模拟)小媛在物理实验课上研究光的折射现象,了解到当光从空气射入介质时,折射率(i为入射角,r为折射角).如图,一束光从空气射向横截面为直角三角形的硫系玻璃透镜斜面,经折射后沿垂直AC边的方向射出.若i=30°,AB=20cm,BC=5cm,则该玻璃透镜的折射率n为( )
A.2 B.1.6 C.1.5 D.1.4
5.(2025 南关区模拟)如图,小明在点C处测得树的顶端A仰角为α,同时测得BC=15m,则树的高度AB为( )
A.15tanα m B.m C.15sinα m D.m
6.(2025 鲁山县一模)我国纸伞的制作工艺十分巧妙.如图,两条伞骨所成的角∠BAC=130°,点D在伞柄AP上,AE=AF=DE=DF=m,则AD的长度可表示为( )
A.msin65° B.mcos65° C.2msin65° D.2mcos65°
7.(2025 长春模拟)许多大型商场购物中心为了引导人流前往目标楼层,会考虑使用“飞梯”(可以跨楼层抵达的超高超长的自动扶梯).上海大悦城的“飞梯”从3层直达7层,“飞梯”的截面如图,AB的长为50米,AB与AC的夹角为24°,则高BC是( )
A.50sin24°米 B.50cos24°米
C.米 D.米
8.(2025 南关区校级三模)如图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图经测量,钢条AB=AC=a厘米,∠ABC=θ.则车位锁的底盒长BC为( )
A.a cosθ厘米 B.a sinθ厘米
C.2a cosθ厘米 D.2a sinθ厘米
9.(2025 朝阳区校级二模)如图所示的是一段索道的示意图.已知A、B两点间的距离为500米,∠BAC=α,则缆车从A点到B点上升的高度(即线段BC的长)为( )
A.米 B.500sinα米 C.米 D.500cosα米
10.(2025 上蔡县三模)近年来,随着智能技术的发展,智能机器人已经应用于社会生活的各个方面.如图是一款智能送货机器人的侧面示意图,现测得其矩形底座ABCD的高BC为20cm,上部显示屏EF的长度为60cm,侧面支架EC的长度为130cm,∠ECD=80°,∠FEC=130°,则该机器人的最高点F距地面AB的高度为( )
A.(30+130sin80°)cm B.(50+130cos80°)cm
C. D.(50+130sin80°)cm
二.填空题(共5小题)
11.(2025 武汉)某科技小组用无人机测量一池塘水面两端A,B的距离,具体过程如下:如图,将无人机垂直上升至距水面120m的P处,测得A处的俯角为45°,B处的俯角为22°,则A,B之间的距离是 m.(tan22°取0.4)
12.(2025 广州)如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,已知cos∠CAD,AB=26,则点B到AD的距离为 .
13.(2025 椒江区校级模拟)如图,四边形ABCD中,若∠B+∠D=180°,BC=CD=3,AC=8,AB=x,AD=y.则xy= .
14.(2025 金凤区模拟)如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求A、B两点间的距离等于 (结果精确到0.1米,参考数据:1.732).
15.(2025 光泽县模拟)具有对称性且富有节奏感的正六边形,不仅为建筑和装饰增添了现代感,还能与多种设计风格相融合.如图1是阅览室墙上设计的正六边形蜂窝状置物架,将该置物架抽象成几何图形如图2所示,若每个正六边形的边长均为2,则该置物架所占用墙面的长度d的值为 .
三.解答题(共5小题)
16.(2025 天河区校级四模)人们经常使用电脑,若坐姿不正确,容易造成眼睛疲劳,腰酸颈痛.使用电脑时一般正确的坐姿是:当眼睛望向显示器屏幕时,“视线角”α为20°(望向屏幕上边缘的水平视线与望向屏幕中心的视线的夹角),小臂水平放在桌面上,肘部形成的“手肘角”β为100°,如图①所示.
(1)如图②,当水平视线AB与屏幕BC垂直,“视线角”α为20°,BC=24cm时,求眼睛与屏幕的距离AB;(结果保留一位小数)
(2)如图③,肩膀到水平地面的距离DG=100cm,大臂DE=30cm,小臂水平放在桌面EF上,若要保证坐姿正确,即“手肘角”β为100°时,求当桌面EF到地面的距离FH为多少?(结果保留一位小数)
参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin80°≈0.98,cos80°≈0.17,tan80°≈5.67
17.(2025 永寿县校级模拟)“生命之树”(如图①)是以西安古观音禅寺的千年银杏树为原型,用建筑和自然结合的方式打造的城市特色建筑景观.如图②,由于“生命之树”主体底部不可直接测量,小兴计划利用无人机测量该“生命之树”主体的高度,他先用无人机从地面上的点D处竖直上升100m到达点C处,在点C处测得“生命之树”主体AB的顶点A处的俯角为22°,然后操控无人机向主体AB的方向水平飞行65m至点E处,在点E处测得顶点A处的俯角为45°,点B,D在同一水平线上,AB⊥BD,图中所有点均在同一平面内,求“生命之树”主体AB的高度.(结果保留整数,参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
18.(2025 广东模拟)图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1m,主臂MP长为5m,测得主臂伸展角.∠PME=37°.(参考数据:sin37°,tan37°,sin53°,tan53°)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q,此时∠QPM=90°,求Q点到N点的距离.
19.(2025 武安市二模)淇淇家位于学校正东方向200m处,周末她和同学约好去学校附近的体育馆打篮球,已知体育馆位于学校北偏西53°方向,距离学校500m.
(1)请根据描述画出淇淇家、学校和体育馆的方位示意图;
(2)求体育馆到淇淇家的直线距离;
(3)若淇淇步行从家出发,先以50m/min的速度匀速走到学校,但到达学校后,发现忘带篮球,于是立即以60m/min的速度原路返回家中.取到篮球后,为了赶时间,她以80m/min的速度从家直接走到体育馆,求淇淇全程所用的时长.(计算结果保留整数.参考数据:sin53°=0.8,
20.(2025 凌河区校级三模)如图1,某款线上教学设备由底座、支撑臂AB、连杆BC、悬臂CD和安装在D处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图.已知支撑臂AB⊥l,AB=18cm,CD=44cm,固定∠ABC=148°,可通过调试悬臂CD与连杆BC的夹角来提高拍摄效果.悬臂端点C到桌面l的距离约为52cm.
(1)BC的长度为多少?
(2)已知摄像头点D到桌面l的距离为30cm时拍摄效果较好,那么此时悬臂CD与连杆BC的夹角∠BCD的度数约为多少?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
2026年中考数学一轮复习 锐角三角函数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 港北区三模)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】C
【分析】根据题意结合图形可知β是重力G与斜面形成的三角形的外角,从而可求得β的度数.
【解答】解:∵重力G的方向竖直向下,
∴重力G与水平方向夹角为90°,
由题意可得:
∴β=∠1=α+90°=115°,
故选:C.
【点评】本题考查了平行线的性质和三角形外角性质,正确进行计算是解题关键.
2.(2025 安庆二模)如图,在正方形网格中,△ABC的位置如图,其中点A、B、C分别在格点上,则tanA的值是( )
A. B. C. D.
【考点】解直角三角形.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】取格点D,连接CD,设每个小正方形的边长为1,由勾股定理结合勾股定理逆定理可得△ACD为直角三角形,且∠ADC=90°,再由正切的定义计算即可得解.
【解答】解:如图所示:取格点D,连接CD,
设每个小正方形的边长为1,由勾股定理可得:
,,,
∴AC2=AD2+CD2,
∴△ACD为Rt△,且∠ADC=90°,
∴tanA,
故选:B.
【点评】本题考查了勾股定理、勾股定理逆定理、求角的正切值,熟练掌握以上知识点是关键.
3.(2025 旬邑县校级模拟)如图,在△ABC中,∠B=45°,BC=3,,则中线AD的长为( )
A. B.2 C. D.
【考点】解直角三角形.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】过点A作AE⊥BC于点E,设AE=x,分别在Rt△ABE和Rt△AEC中,利用锐角三角函数的定义求出BE和CE的长,从而列出关于x的方程,进而求出BC的长,再利用三角形的中线定义求出BD的长,从而求出DE的长,最后在Rt△ADE中,利用勾股定理进行计算即可解答.
【解答】解:过点A作AE⊥BC于点E,
设AE=x,
在Rt△ABE中,∠B=45°,
∴BE=AE tan45°=x,
在Rt△AEC中,tanC
∴,
∴CE=2AE=2x,
∴BC=BE+CE,
∴x+2x=3,
解得:x=1,
∴AE=BE=1,
∵AD是BC边上的中线,
∴BD=CDBC=1.5,
∴DE=BD﹣BE=1.5﹣1=0.5,
在Rt△ADE中,
故选:D.
【点评】本题考查了解直角三角形,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
4.(2025 莆田模拟)小媛在物理实验课上研究光的折射现象,了解到当光从空气射入介质时,折射率(i为入射角,r为折射角).如图,一束光从空气射向横截面为直角三角形的硫系玻璃透镜斜面,经折射后沿垂直AC边的方向射出.若i=30°,AB=20cm,BC=5cm,则该玻璃透镜的折射率n为( )
A.2 B.1.6 C.1.5 D.1.4
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用.
【答案】A
【分析】由题意得β+∠A=90°,r+β=90°,则r=∠A,所以,然后通过折射率即可求解.
【解答】解:如图,
∵折射光线沿垂直AC边的方向射出β+∠A=90°,
∵法线垂直于AB,
∴r+β=90°,
∴r=∠A,
∴,
∵折射率,
故选:A.
【点评】本题考查了解直角三角形的应用,同角的余角相等,掌握知识点的应用是解题的关键.
5.(2025 南关区模拟)如图,小明在点C处测得树的顶端A仰角为α,同时测得BC=15m,则树的高度AB为( )
A.15tanα m B.m C.15sinα m D.m
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】A
【分析】由锐角三角函数定义得tanα,即可得出答案.
【解答】解:在Rt△ABC中,BC=15m,∠ACB=α,tanα,
∴AB=BC tanα=15tanα(m).
故选:A.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题及坡度坡角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
6.(2025 鲁山县一模)我国纸伞的制作工艺十分巧妙.如图,两条伞骨所成的角∠BAC=130°,点D在伞柄AP上,AE=AF=DE=DF=m,则AD的长度可表示为( )
A.msin65° B.mcos65° C.2msin65° D.2mcos65°
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】连接EF交AD于点O,根据已知易得:四边形AEDF是菱形,从而利用菱形的性质可得OA=ODAD,∠AOF=90°,∠FAD=65°,然后在Rt△AOF中,利用锐角三角函数的定义求出AO的长,从而求出AD的长,即可解答.
【解答】解:连接EF交AD于点O,
∵AE=AF=DE=DF=m,
∴四边形AEDF是菱形,
∴OA=ODAD,∠AOF=90°,∠FAD∠EAF=65°,
在Rt△AOF中,AO=AF cos65°=mcos65°,
∴AD=2AO=2mcos65°,
∴AD的长度可表示为2mcos65°,
故选:D.
【点评】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
7.(2025 长春模拟)许多大型商场购物中心为了引导人流前往目标楼层,会考虑使用“飞梯”(可以跨楼层抵达的超高超长的自动扶梯).上海大悦城的“飞梯”从3层直达7层,“飞梯”的截面如图,AB的长为50米,AB与AC的夹角为24°,则高BC是( )
A.50sin24°米 B.50cos24°米
C.米 D.米
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;几何直观;运算能力.
【答案】A
【分析】根据图形和锐角三角函数,可以表示出BC的值.
【解答】解:∵∠BCA=90°,AB=50m,∠A=24°,
∴sinA,
∴BC=50sinA=50sin24°(米),
故选:A.
【点评】本题考查解直角三角形的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
8.(2025 南关区校级三模)如图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图经测量,钢条AB=AC=a厘米,∠ABC=θ.则车位锁的底盒长BC为( )
A.a cosθ厘米 B.a sinθ厘米
C.2a cosθ厘米 D.2a sinθ厘米
【考点】解直角三角形的应用;等腰三角形的性质.
【专题】解直角三角形及其应用;运算能力.
【答案】C
【分析】根据题意,结合图形,在Rt△ADB中利用三角函数得到BD,结合等腰三角形的性质得到结果.
【解答】解:过A点作AD⊥BC于D点,
∵AB=AC,△ABC是等腰三角形,
∴BD=DC,
∵在Rt△ADB中,∠ADB=90°,∠ABD=θ,AB=a厘米,
∴BD=AB cos∠ABD=a cosθ(厘米),
∴BC=2a cosθ(厘米),
故选:C.
【点评】本题考查了解直角三角形的应用,熟练掌握解直角三角形是解题的关键.
9.(2025 朝阳区校级二模)如图所示的是一段索道的示意图.已知A、B两点间的距离为500米,∠BAC=α,则缆车从A点到B点上升的高度(即线段BC的长)为( )
A.米 B.500sinα米 C.米 D.500cosα米
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】根据题意可得:BC⊥AC,然后在Rt△ABC中,利用锐角三角函数的定义求出BC的长,即可解答.
【解答】解:由题意得:BC⊥AC,
在Rt△ABC中,∠BAC=α,AB=500米,
∴BC=AB sinα=500sinα(米),
∴缆车从A点到B点上升的高度为500sinα米,
故选:B.
【点评】本题考查了解直角三角形的应用,准确熟练地进行计算是解题的关键.
10.(2025 上蔡县三模)近年来,随着智能技术的发展,智能机器人已经应用于社会生活的各个方面.如图是一款智能送货机器人的侧面示意图,现测得其矩形底座ABCD的高BC为20cm,上部显示屏EF的长度为60cm,侧面支架EC的长度为130cm,∠ECD=80°,∠FEC=130°,则该机器人的最高点F距地面AB的高度为( )
A.(30+130sin80°)cm B.(50+130cos80°)cm
C. D.(50+130sin80°)cm
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】过点E,F分别作EH⊥CD,FN⊥CD,垂足分别为H,N,过点E作EM⊥FN,垂足为M,可得四边形EMNH为矩形,即得MN=EH,再分别解Rt△EHC和Rt△FEM,求出EH、FM即可求解.
【解答】解:过点E,F分别作EH⊥CD,FN⊥CD,垂足分别为H,N,过点E作EM⊥FN,垂足为M,则四边形EMNH为矩形,
∴MN=EH,
∵,
∴EH=CE sin∠ECH=130sin80°(cm),
∴MN=130sin80°(cm),
∵∠EHC=90°,
∴∠CEH=90°﹣80°=10°,
∴∠FEM=∠FEC﹣∠MEH﹣∠CEH=130°﹣90°﹣10°=30°,
∴,
∴点F距地面AB的高度为FM+MN+BC=30+130sin80°+20=(50+130sin80°)cm,
故选:D.
【点评】本题考查了解直角三角形的应用,矩形的判定和性质,正确进行计算是解题关键.
二.填空题(共5小题)
11.(2025 武汉)某科技小组用无人机测量一池塘水面两端A,B的距离,具体过程如下:如图,将无人机垂直上升至距水面120m的P处,测得A处的俯角为45°,B处的俯角为22°,则A,B之间的距离是 180 m.(tan22°取0.4)
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】180.
【分析】根据题意可得:PD∥CB,从而可得∠PAC=∠DPA=45°,∠DPB=∠PBC=22°,然后分别在Rt△PAC和Rt△PBC中,利用锐角三角函数的定义求出AC和BC的长,从而进行计算即可解答.
【解答】解:如图:
由题意得:PD∥CB,
∴∠PAC=∠DPA=45°,∠DPB=∠PBC=22°,
在Rt△PAC中,PC=120m,
∴AC120(m),
在Rt△PBC中,∠PBC=22°,
∴BC300(m),
∴AB=BC﹣AC=300﹣120=180(m),
∴A,B之间的距离约是180m,
故答案为:180.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,根据题目的已知条件并结合图形进行分析添加适当的辅助线是解题的关键.
12.(2025 广州)如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,已知cos∠CAD,AB=26,则点B到AD的距离为 10 .
【考点】解直角三角形;角平分线的性质.
【专题】解直角三角形及其应用;运算能力.
【答案】10.
【分析】过点D作DH⊥AB于点H.可以假设AC=12k,AD=13k,则CD=5k,证明DH=CD=5k,利用面积法求解.
【解答】解:过点D作DH⊥AB于点H.
∵∠C=90°,cos∠CAD,
∴可以假设AC=12k,AD=13k,则CD=5k,
∵AD平分∠CAB,DC⊥AC,DH⊥AB,
∴DH=DC=5k,
设点B到AD的距离为h,则有13k×h26×5k,
解得h=10.
故答案为:10.
【点评】本题考查解直角三角形,角平分线的性质,解题的关键是学会利用参数构建方程解决问题.
13.(2025 椒江区校级模拟)如图,四边形ABCD中,若∠B+∠D=180°,BC=CD=3,AC=8,AB=x,AD=y.则xy= 55 .
【考点】解直角三角形.
【专题】三角形;解直角三角形及其应用;几何直观;运算能力;推理能力.
【答案】55.
【分析】过点C作CE⊥AB于点E,CF⊥AD,交AD延长线于点F,证明∠B=∠CDF=α,解Rt△BCE得CE=3sinα,BE=3cosα,则AE=x﹣3cosα,由勾股定理得AE2+CE2=AC2,则(x﹣3cosα)2+(3sinα)2=82,整理得x2﹣6xcosα=55①,解Rt△CDF得CF=3sinα,DF=3cosα,则AF=y+3cosα,由勾股定理得AF2+CF2=AC2,则(y+3cosα)2+(3sinα)2=82,整理得y2+6ycosα=55②,由①②得x2﹣6xcosα=y2+6ycosα,由此得x﹣y=6cosα,则x2+y2﹣2xy=36cos2α,再由①+②得x2+y2=110+36cos2α,进而得110+36cos2α﹣2xy=36cos2α,由此即可得出xy的值.
【解答】解:过点C作CE⊥AB于点E,CF⊥AD,交AD的延长线于点F,如图所示:
∵∠B+∠ADC=180°,∠CDF+∠ADC=180°,
∴∠B=∠CDF,
设∠B=∠CDF=α,
在Rt△BCE中,∠B=α,BC=3,
∴sinα,cosα,
∴CE=BC sinα=3sinα,BE=BC cosα=3cosα,
∵AB=x,
∴AE=AB﹣BE=x﹣3cosα,
在Rt△ACE中,AC=8,
由勾股定理得:AE2+CE2=AC2,
∴(x﹣3cosα)2+(3sinα)2=82,
整理得:x2﹣6xcosα+9(sin2α+cos2α)=64,
∵sin2α+cos2α=1,
∴x2﹣6xcosα=55①,
在Rt△CDF中,∠CDF=α,CD=3,
∴sinα,cosα,
∴CF=CD sinα=3sinα,DF=CD cosα=3cosα,
∵AD=y,
∴AF=AD+DF=y+3cosα,
在Rt△ACF中,AC=8,
由勾股定理得:AF2+CF2=AC2,
∴(y+3cosα)2+(3sinα)2=82,
整理得:y2+6ycosα+9(sin2α+cos2α)=64,
∵sin2α+cos2α=1,
∴y2+6ycosα=55②,
由①②得:x2﹣6xcosα=y2+6ycosα,
∴(x+y)(x﹣y)=6(x+y)cosα,
∵x+y≠0,
∴x﹣y=6cosα,
∴(x﹣y)2=(6cosα)2,
∴x2+y2﹣2xy=36cos2α,
由①+②得:x2﹣6xcosα+y2+6ycosα=110,
∴x2+y2=110+6(x﹣y)cosα=110+6×6cosα×cosα,
∴x2+y2=110+36cos2α,
∴110+36cos2α﹣2xy=36cos2α,
∴xy=55.
故答案为:55.
【点评】此题主要考查了解直角三角形,熟练掌握锐角三角函数的定义,勾股定理,完全平方公式的结构特征是解决问题的关键.
14.(2025 金凤区模拟)如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
(1)山坡坡角(即∠ABC)的度数等于 30 度;
(2)求A、B两点间的距离等于 34.6 (结果精确到0.1米,参考数据:1.732).
【考点】解直角三角形的应用﹣仰角俯角问题.
【答案】见试题解答内容
【分析】(1)根据俯角以及坡度的定义即可求解;
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
【解答】解:(1)∵tan∠ABC=1:,
∴∠ABC=30°;
(2)由题意得:∠PBH=60°,
∵∠ABC=30°,
∴∠ABP=90°,又∠APB=45°,
∴△PAB为等腰直角三角形,
在直角△PHB中,PB20.
在直角△PBA中,AB=PB=2034.6米.
故答案为30,34.6.
【点评】本题主要考查了俯角的问题以及坡度的定义,正确利用三角函数是解题的关键.
15.(2025 光泽县模拟)具有对称性且富有节奏感的正六边形,不仅为建筑和装饰增添了现代感,还能与多种设计风格相融合.如图1是阅览室墙上设计的正六边形蜂窝状置物架,将该置物架抽象成几何图形如图2所示,若每个正六边形的边长均为2,则该置物架所占用墙面的长度d的值为 19 .
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】19.
【分析】根据题意可得:点A,B,C,D,E,F,G,H共线,连接AB并延长到点H,则AH⊥HM,根据题意可得:AB=CD=EF=4,BC=DE=FG=GM=2,然后在Rt△GHM中,利用锐角三角函数的定义求出GH的长,最后进行计算即可解答.
【解答】解:如图:由题意得:点A,B,C,D,E,F,G,H共线,连接AB并延长到点H,则AH⊥HM,
由题意得:AB=CD=EF=4,BC=DE=FG=GM=2,
在Rt△GHM中,∠MGH=60°,
∴GH=GM cos60°=21,
∴AH=AB+BC+CD+DE+EF+FG+GH=4+2+4+2+4+2+1=19,
∴该置物架所占用墙面的长度d的值为19,
故答案为:19.
【点评】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添适当的辅助线是解题的关键.
三.解答题(共5小题)
16.(2025 天河区校级四模)人们经常使用电脑,若坐姿不正确,容易造成眼睛疲劳,腰酸颈痛.使用电脑时一般正确的坐姿是:当眼睛望向显示器屏幕时,“视线角”α为20°(望向屏幕上边缘的水平视线与望向屏幕中心的视线的夹角),小臂水平放在桌面上,肘部形成的“手肘角”β为100°,如图①所示.
(1)如图②,当水平视线AB与屏幕BC垂直,“视线角”α为20°,BC=24cm时,求眼睛与屏幕的距离AB;(结果保留一位小数)
(2)如图③,肩膀到水平地面的距离DG=100cm,大臂DE=30cm,小臂水平放在桌面EF上,若要保证坐姿正确,即“手肘角”β为100°时,求当桌面EF到地面的距离FH为多少?(结果保留一位小数)
参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin80°≈0.98,cos80°≈0.17,tan80°≈5.67
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;应用意识.
【答案】(1)眼睛与屏幕的距离AB约为66.7cm;
(2)桌面EF到地面的距离FH约为70.6cm.
【分析】(1)根据BC的长及20°的正切值可得AB的长;
(2)易得∠DEM=80°,根据DE的长和80°的正弦值可得MG的长,取DG的长,减去MG的长即为桌面EF到地面的距离.
【解答】解:(1)∵AB⊥BC,
∴∠B=90°,
∵α=20°,BC=24cm,
∴AB66.7(cm),
答:眼睛与屏幕的距离AB约为66.7cm;
(2)由题意得:四边形GMFH是矩形,∠DME=90°,
∵β=100°,
∴∠DEM=80°,
∵DE=30cm,
∴DM=DE sin80°≈30×0.98≈29.4(cm),
∵DG=100cm,
∴GM=100﹣29.4=70.6(cm),
∴FH=GM=70.6cm.
答:桌面EF到地面的距离FH约为70.6cm.
【点评】本题考查解直角三角形的应用.掌握锐角三角函数的性质是解决本题的关键.
17.(2025 永寿县校级模拟)“生命之树”(如图①)是以西安古观音禅寺的千年银杏树为原型,用建筑和自然结合的方式打造的城市特色建筑景观.如图②,由于“生命之树”主体底部不可直接测量,小兴计划利用无人机测量该“生命之树”主体的高度,他先用无人机从地面上的点D处竖直上升100m到达点C处,在点C处测得“生命之树”主体AB的顶点A处的俯角为22°,然后操控无人机向主体AB的方向水平飞行65m至点E处,在点E处测得顶点A处的俯角为45°,点B,D在同一水平线上,AB⊥BD,图中所有点均在同一平面内,求“生命之树”主体AB的高度.(结果保留整数,参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】“生命之树”主体AB的高度约为57m.
【分析】如图,过点A作 AF⊥CE,交CE的延长线于点F,根据矩形的性质得到BF=CD=100m,由题意知∠ACF=22°,∠AEF=45°,CE=65m,求得EF=AF,设EF=AF=x m,则CF=CE+EF=(65+x)m,解直角三角形即可得到结论.
【解答】解:如图,过点A作 AF⊥CE,交CE的延长线于点F,
∵点B,D在同一水平线上,AB⊥BD,
∴四边形CDBF为矩形,
∴BF=CD=100m,
由题意知∠ACF=22°,∠AEF=45°,CE=65m,
∴EF=AF,
设EF=AF=x m,则CF=CE+EF=(65+x)m,
在Rt△ACF中,,
∴,
解得x≈43.3,
∴AF=43.3m,
∴AB=100﹣43.3=56.7=57(m),
答:“生命之树”主体AB的高度约为57m.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,正确地作出辅助线是解题的关键.
18.(2025 广东模拟)图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1m,主臂MP长为5m,测得主臂伸展角.∠PME=37°.(参考数据:sin37°,tan37°,sin53°,tan53°)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q,此时∠QPM=90°,求Q点到N点的距离.
【考点】解直角三角形的应用.
【专题】计算题;数形结合;解直角三角形及其应用;运算能力;应用意识.
【答案】(1)点P到地面的高度约为4m;
(2)Q点到N点的距离约为7m.
【分析】(1)作PB⊥QN于点B,延长ME交PB于点A.易得四边形ABNM是矩形,那么AB=MN,AM=BN,根据37°的正弦值和PM的长可得PA的长,加上AB的长即为点P到地面的高度;
(2)根据勾股定理可得AM的长,也就是BN的长,根据∠QPM=90°,可得∠QPB=37°,根据37°的正切值和PB的长可得QB的长,加上BN的长即为Q点到N点的距离.
【解答】解:(1)作PB⊥QN于点B,延长ME交PB于点A.
∴∠PBQ=∠PBN=90°.
∵EM∥QN,
∴∠BAE=∠PAE=90°.
由题意得:MN⊥BN,
∴∠MNB=90°.
∴四边形ABNM是矩形.
∴AB=MN=1(m),AM=BN.
∵PM=5m,∠PME=37°,
∴PA=PM sin∠PME≈53(m).
∴PB=PA+AB=3+1=4(m).
答:点P到地面的高度约为4m;
(2)∵PA=3m,PM=5m,∠PAM=90°,
∴AM=4(m),∠APM+∠PME=90°.
∴BN=4(m).
∵∠QPM=90°,
∴∠QPB+∠APM=90°.
∴∠QPB=∠PME=37°.
∴QB=PB tan∠QPB≈43(m).
∴QN=QB+BN=7(m).
答:Q点到N点的距离约为7m.
【点评】本题考查解直角三角形的应用.把所给的线段和角整理到合适的直角三角形中是解决本题的关键.
19.(2025 武安市二模)淇淇家位于学校正东方向200m处,周末她和同学约好去学校附近的体育馆打篮球,已知体育馆位于学校北偏西53°方向,距离学校500m.
(1)请根据描述画出淇淇家、学校和体育馆的方位示意图;
(2)求体育馆到淇淇家的直线距离;
(3)若淇淇步行从家出发,先以50m/min的速度匀速走到学校,但到达学校后,发现忘带篮球,于是立即以60m/min的速度原路返回家中.取到篮球后,为了赶时间,她以80m/min的速度从家直接走到体育馆,求淇淇全程所用的时长.(计算结果保留整数.参考数据:sin53°=0.8,
【考点】解直角三角形的应用﹣方向角问题;作图—应用与设计作图.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)方位示意图见解析部分;
(2)体育馆到淇淇家的直线距离约为660米;
(3)淇淇全程所用的时长为15.6min.
【分析】(1)根据题意,画出方位示意图即可;
(2)结合图形,在Rt△ACD中求出AD,CD,在Rt△BCD中利用勾股定理即可求出BC;
(3)根据题意,分别计算出淇淇每段路程所用的时间,即可得到总用时.
【解答】解:(1)淇淇家、学校和体育馆的方位示意图如图1所示,
(2)如图2,过C点作CD⊥AB,并BA的延长线于点D,
依题意,∠DCA=53°,AB=200米,AC=500米,
∴在Rt△ACD中,AD=AC sin∠DCA=500×sin53°≈400(米),
CD=AC cos∠DCA=500×cos53°≈300(米),
∴BD=AD+AB=400+200=600(米),
∵在Rt△BCD中,BC2=BD2+CD2=6002+3002=450000,
∴BC=300660(米),
答:体育馆到淇淇家的直线距离约为660米;
(3)∵淇淇从家出发以50m/min的速度匀速走到学校,
∴所用时间为200÷50=4(min),
∵以60m/min的速度原路返回家中,
∴所用时间为200÷60(min),
∵以80m/min的速度从家直接走到体育馆,
∴所用时间为660÷80=8.25(min),
∴淇淇全程所用的时长为48.25≈15.6(min),
答:淇淇全程所用的时长为15.6min.
【点评】本题考查了解直角三角形的应用,熟练掌握解直角三角形是解题的关键.
20.(2025 凌河区校级三模)如图1,某款线上教学设备由底座、支撑臂AB、连杆BC、悬臂CD和安装在D处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图.已知支撑臂AB⊥l,AB=18cm,CD=44cm,固定∠ABC=148°,可通过调试悬臂CD与连杆BC的夹角来提高拍摄效果.悬臂端点C到桌面l的距离约为52cm.
(1)BC的长度为多少?
(2)已知摄像头点D到桌面l的距离为30cm时拍摄效果较好,那么此时悬臂CD与连杆BC的夹角∠BCD的度数约为多少?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)BC的长度约为40cm;
(2)此时悬臂CD与连杆BC的夹角∠BCD的度数约为28°.
【分析】(1)过点C作CE⊥l,垂足为E,过点B作BF⊥CE,垂足为F,根据题意可得:∠ABF=90°,AB=EF=18cm,CE=52cm,从而可得CF=34cm,∠CBF=58°,然后在Rt△CBF中,利用锐角三角函数的定义进行计算即可解答;
(2)过点D作DG⊥CE,垂足为G,根据题意可得:EG=30cm,AB∥CE,从而可得∠BCE=32°,CG=22cm,然后在Rt△CDG中,利用锐角三角函数的定义可得cos∠DCG,从而可得∠DCG=60°,最后利用角的和差关系进行计算即可解答.
【解答】解:(1)过点C作CE⊥l,垂足为E,过点B作BF⊥CE,垂足为F,
由题意得:∠ABF=90°,AB=EF=18cm,CE=52cm,
∴CF=CE﹣EF=34(cm),
∵∠ABC=148°,
∴∠CBF=∠ABC﹣∠ABF=58°,
在Rt△CBF中,BC40(cm),
∴BC的长度约为40cm;
(2)过点D作DG⊥CE,垂足为G,
由题意得:EG=30cm,AB∥CE,
∴∠BCE=180°﹣∠ABC=32°,
∵CE=52cm,
∴CG=CE﹣EG=52﹣30=22(cm),
在Rt△CDG中,CD=44cm,
∴cos∠DCG,
∴∠DCG=60°,
∴∠DCB=∠DCG﹣∠BCE=28°,
∴此时悬臂CD与连杆BC的夹角∠BCD的度数约为28°.
【点评】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
