2026年中考数学一轮复习 投影与视图(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 投影与视图(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 04:31:08 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2026年中考数学一轮复习 投影与视图
一.选择题(共10小题)
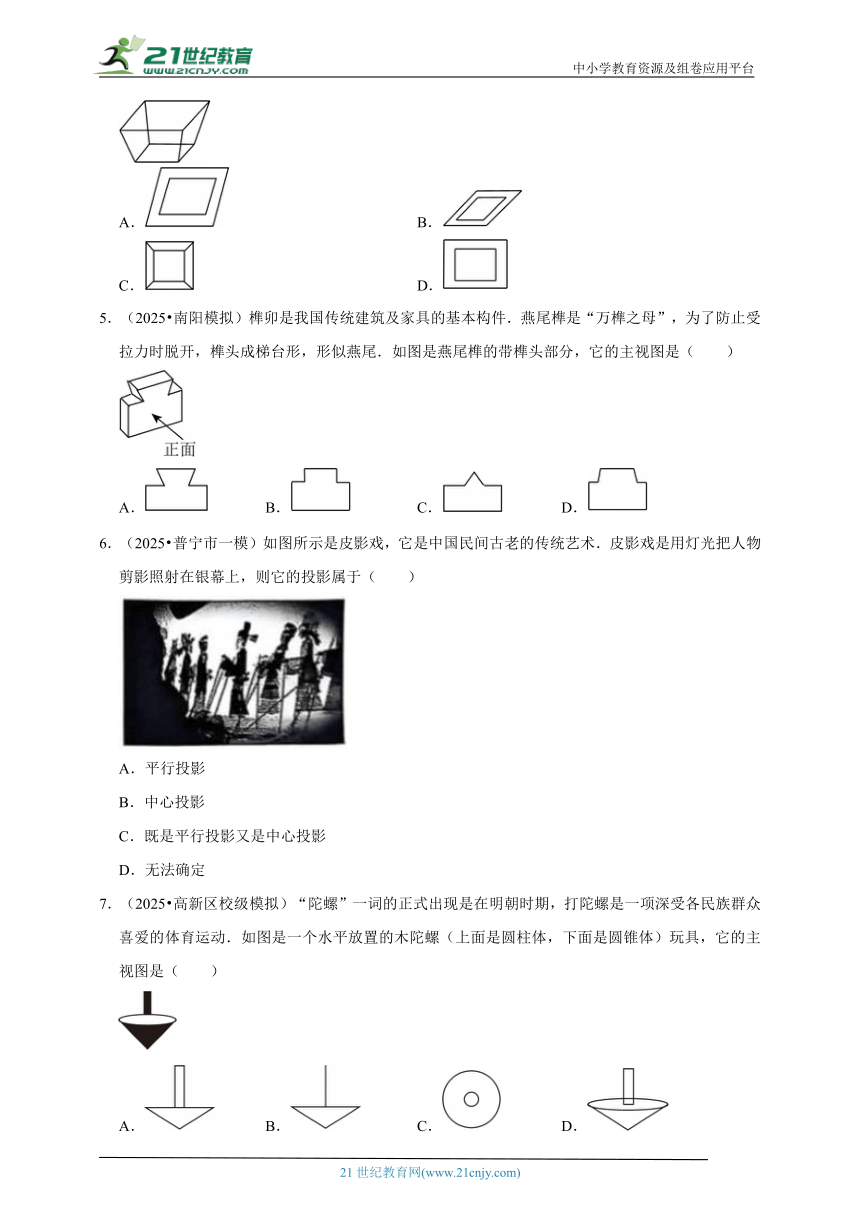
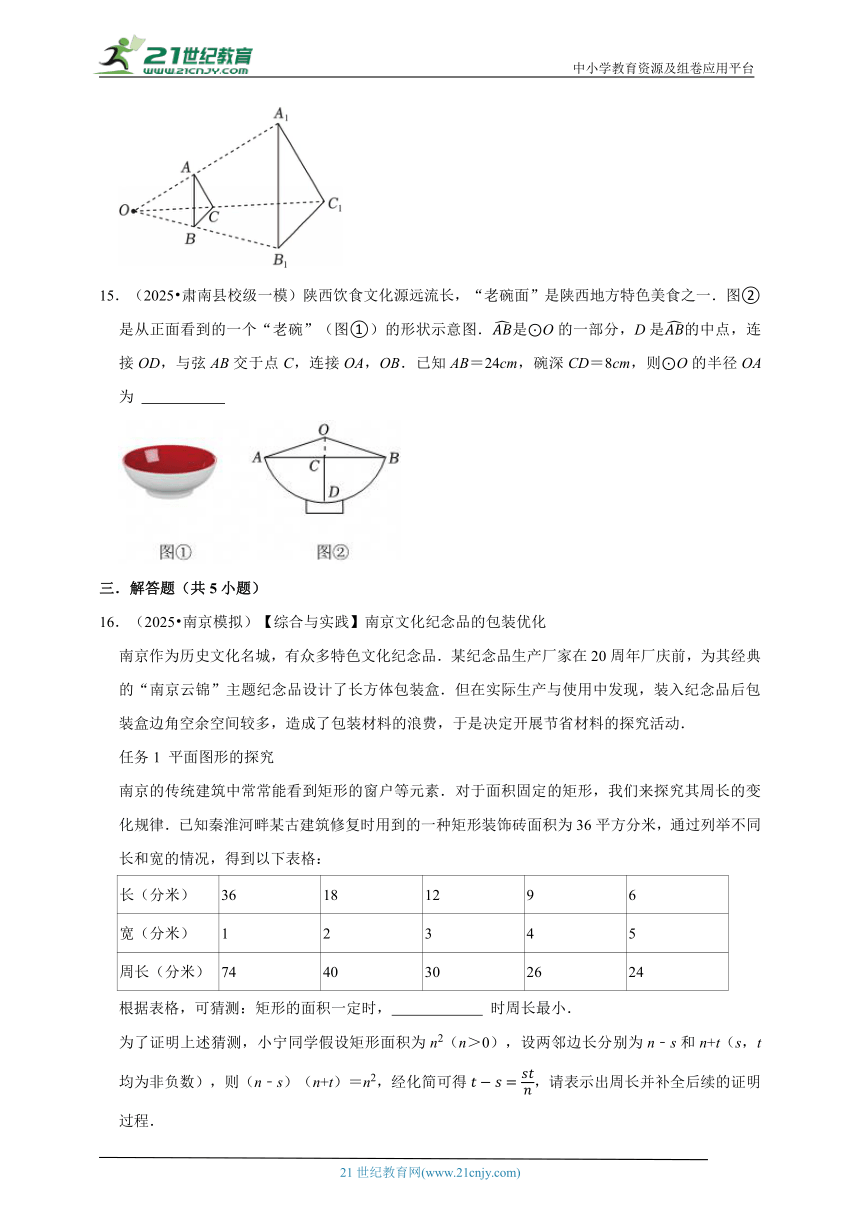
1.(2025 武汉)如图是由五个相同的小正方体组成的几何体,它的俯视图是( )
A. B. C. D.
2.(2025 大同模拟)如图是由5个相同小立方体搭成的几何体,若将小立方体①放到小立方体②的正上方,则关于该几何体变化前后的三视图,下列说法正确的是( )
A.主视图不变,左视图、俯视图改变
B.左视图、俯视图不变,主视图改变
C.主视图、俯视图不变,左视图改变
D.主视图、俯视图、左视图都发生改变
3.(2025 青阳县模拟)如图,两个大小不同的球在水平面上紧紧靠在一起,其俯视图是( )
A. B.
C. D.
4.(2025 宁陵县三模)“斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )
A. B.
C. D.
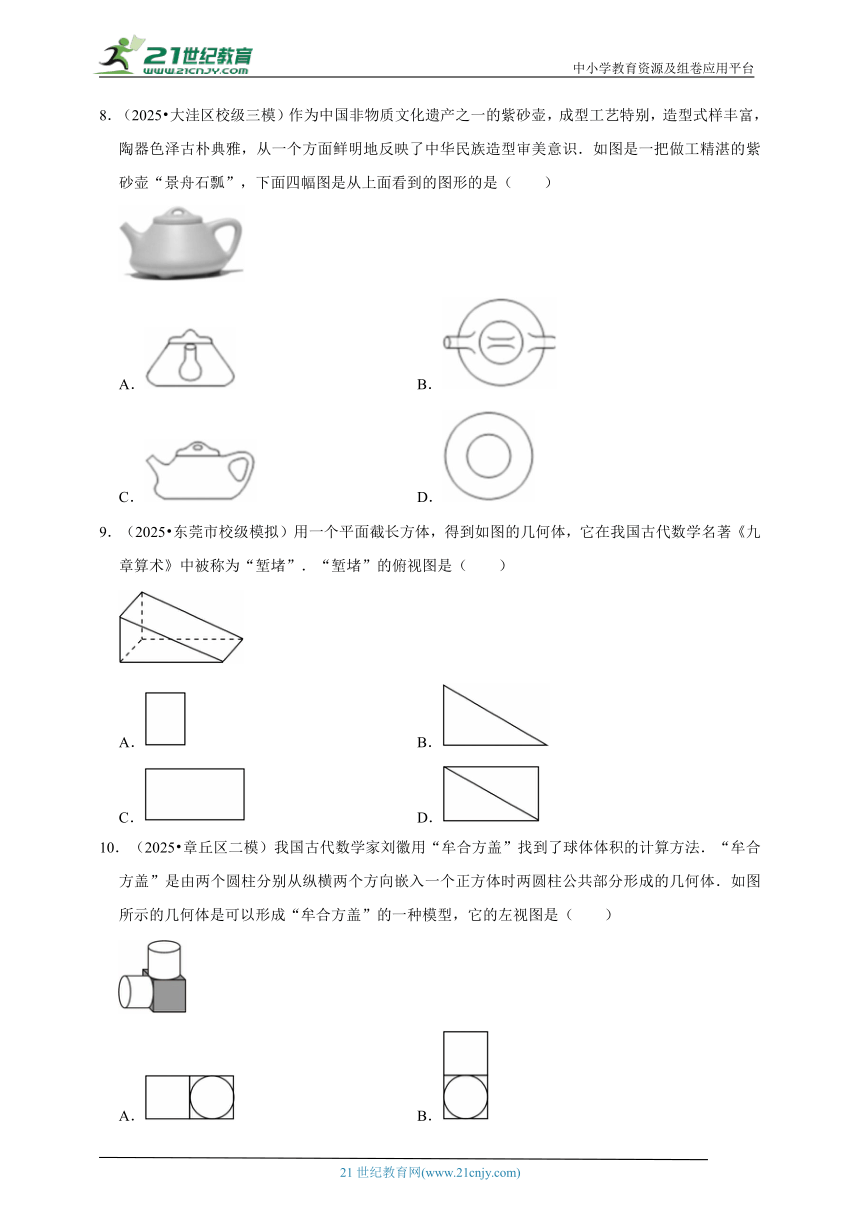
5.(2025 南阳模拟)榫卯是我国传统建筑及家具的基本构件.燕尾榫是“万榫之母”,为了防止受拉力时脱开,榫头成梯台形,形似燕尾.如图是燕尾榫的带榫头部分,它的主视图是( )
A. B. C. D.
6.(2025 普宁市一模)如图所示是皮影戏,它是中国民间古老的传统艺术.皮影戏是用灯光把人物剪影照射在银幕上,则它的投影属于( )
A.平行投影
B.中心投影
C.既是平行投影又是中心投影
D.无法确定
7.(2025 高新区校级模拟)“陀螺”一词的正式出现是在明朝时期,打陀螺是一项深受各民族群众喜爱的体育运动.如图是一个水平放置的木陀螺(上面是圆柱体,下面是圆锥体)玩具,它的主视图是( )
A. B. C. D.
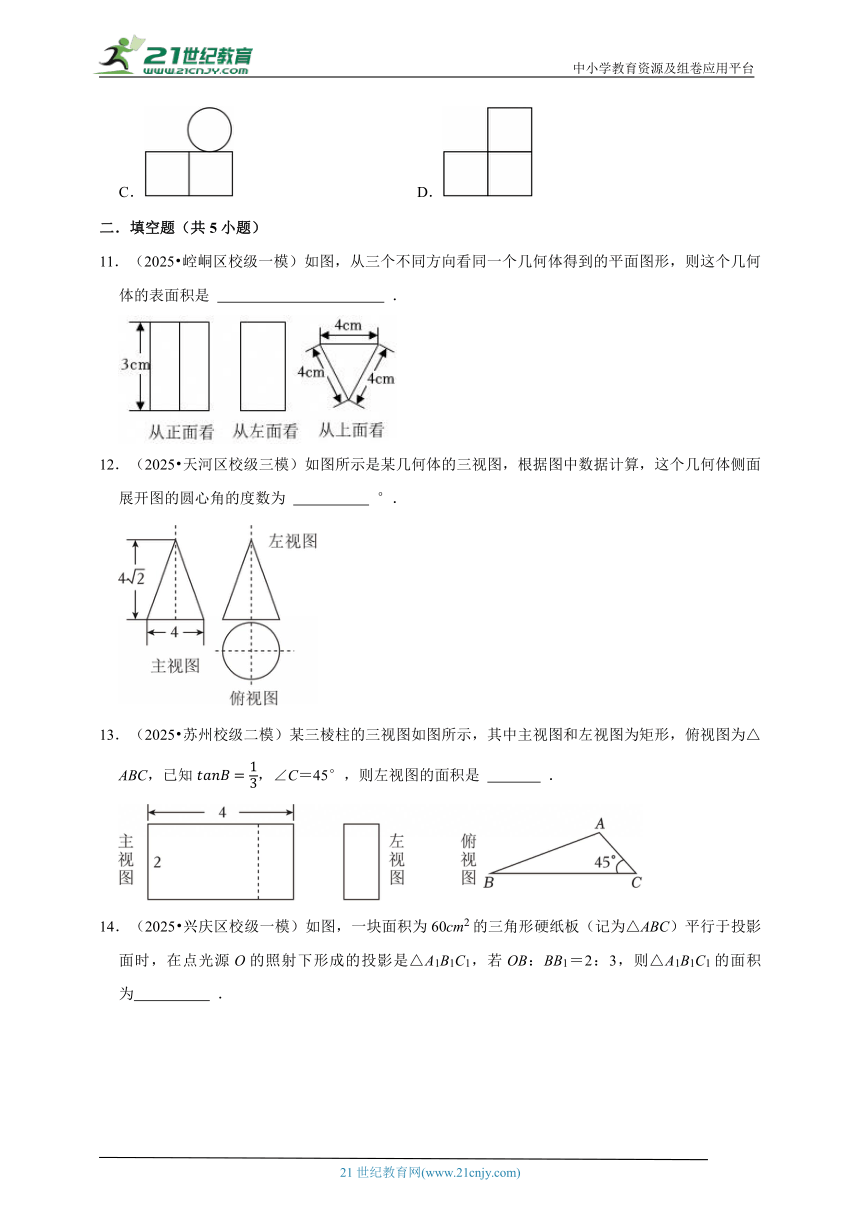
8.(2025 大洼区校级三模)作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.如图是一把做工精湛的紫砂壶“景舟石瓢”,下面四幅图是从上面看到的图形的是( )
A. B.
C. D.
9.(2025 东莞市校级模拟)用一个平面截长方体,得到如图的几何体,它在我国古代数学名著《九章算术》中被称为“堑堵”.“堑堵”的俯视图是( )
A. B.
C. D.
10.(2025 章丘区二模)我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的左视图是( )
A. B.
C. D.
二.填空题(共5小题)
11.(2025 崆峒区校级一模)如图,从三个不同方向看同一个几何体得到的平面图形,则这个几何体的表面积是 .
12.(2025 天河区校级三模)如图所示是某几何体的三视图,根据图中数据计算,这个几何体侧面展开图的圆心角的度数为 °.
13.(2025 苏州校级二模)某三棱柱的三视图如图所示,其中主视图和左视图为矩形,俯视图为△ABC,已知,∠C=45°,则左视图的面积是 .
14.(2025 兴庆区校级一模)如图,一块面积为60cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1,若OB:BB1=2:3,则△A1B1C1的面积为 .
15.(2025 肃南县校级一模)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”(图①)的形状示意图.是⊙O的一部分,D是的中点,连接OD,与弦AB交于点C,连接OA,OB.已知AB=24cm,碗深CD=8cm,则⊙O的半径OA为
三.解答题(共5小题)
16.(2025 南京模拟)【综合与实践】南京文化纪念品的包装优化
南京作为历史文化名城,有众多特色文化纪念品.某纪念品生产厂家在20周年厂庆前,为其经典的“南京云锦”主题纪念品设计了长方体包装盒.但在实际生产与使用中发现,装入纪念品后包装盒边角空余空间较多,造成了包装材料的浪费,于是决定开展节省材料的探究活动.
任务1 平面图形的探究
南京的传统建筑中常常能看到矩形的窗户等元素.对于面积固定的矩形,我们来探究其周长的变化规律.已知秦淮河畔某古建筑修复时用到的一种矩形装饰砖面积为36平方分米,通过列举不同长和宽的情况,得到以下表格:
长(分米) 36 18 12 9 6
宽(分米) 1 2 3 4 5
周长(分米) 74 40 30 26 24
根据表格,可猜测:矩形的面积一定时, 时周长最小.
为了证明上述猜测,小宁同学假设矩形面积为n2(n>0),设两邻边长分别为n﹣s和n+t(s,t均为非负数),则(n﹣s)(n+t)=n2,经化简可得,请表示出周长并补全后续的证明过程.
任务2 立体图形的包装改进
厂家之前设计的长方体包装盒尺寸为:长10厘米、宽8厘米、高6厘米,该包装盒用于包装以南京明城墙为原型的小型纪念品.现打算在保持底面积不变的前提下,将包装盒形状改为底面半径为4厘米的圆柱体,高保持不变,从节省材料(即表面积最小)的角度来看,你觉得这样的改进合理吗?请判断并说明理由.(取3.14,结果精确到0.1平方厘米)
17.(2025 连城县模拟)综合与实践
问题情境 学校准备在一面高2m、宽4m的墙上建一扇拱形门,这面墙的主视图为矩形ABCD,如图1.老师让同学们帮忙设计,要求既美观大方,又尽可能地容易通过.
方案设计 A小组设计的是半圆形拱门,如图2,以AB为直径的半圆O与矩形ABCD三边都相切.
B小组设计的是抛物线形拱门,如图3,抛物线的顶点P在墙的上沿CD的中点处,且抛物线过点A和点B.
提出问题 A,B两小组设计的拱门哪个“通过性”更好呢?
分析问题 老师建议同学们分别计算它们的“内接正方形”(正方形的两个顶点在线段AB上,两个顶点在半圆或抛物线上)面积的大小,通过比较两种设计方案的“内接正方形”的面积,判断它们的“通过性”.
解决问题 请你先分别画出两种方案的“内接正方形”的示意图,然后分别计算它们的面积,并利用计算结果说明哪个方案的拱门“通过性”更好.()
18.(2025 永寿县校级模拟)春夏之交,正适合去山野间漫游,蓝天白云下,青山绿水间,择一处草地,支一顶帐篷,邀亲朋好友,闻清风,话家常,好不惬意.一款帐篷的支架简单,携带方便,适合一般的休闲旅行使用,它的形状可近似看作抛物线,该款帐篷在搭建时,张开的宽度和顶部高度会影响容纳的椅子数量,如图①是该款帐篷搭建完成的平面示意图,其张开的宽度AB=2m,顶部高度MN=1.2m,现以点A为坐标原点,AB所在直线为x轴,过点A且平行于MN的直线为y轴建立平面直角坐标系.
(1)求该帐篷支架对应的抛物线的表达式;
(2)如图②为一把椅子摆入该帐篷后的简易视图,椅子高度EC=0.9m,宽度CD=0.3m,若在该帐篷内沿AB方向摆放一排此款椅子,则最多可摆放多少把椅子?
19.(2025 淮安区校级一模)图1是一个不倒翁模型,图2是它的主视图,由△ABC和以O为圆心的弧组成,已知OC⊥AB,AD=BD=24cm,OD=18cm,CD=32cm.
(1)求证:AC是⊙O的切线;
(2)如图3,转动模型使AC与地面EF平行,求此时点B到地面的距离BF的长度.
20.(2025 安阳县二模)某设计师结合数学知识设计了一款沙发,沙发的三视图如图1所示,将沙发侧面示意图简化后,得到图2所示图形.为了解沙发的相关性能,设计师将图形放入平面直角坐标系中,其中曲线AB是反比例函数的一段图象,线段BD是一次函数的一段图象,点B的坐标为(25,40),沙发腿DE⊥x轴,BC与x轴交于点C.请你根据图形解决以下问题:
(1)请求出反比例函数和一次函数的表达式;(不要求写x的取值范围)
(2)过点A向x轴作垂线,交x轴于点F.已知CF=7cm,CE=33cm,DE=45cm,设计师想用一个长方体箱子将沙发放进去,则这个长方体箱子的长、宽、高至少分别是多少?
2026年中考数学一轮复习 投影与视图
参考答案与试题解析
一.选择题(共10小题)
1.(2025 武汉)如图是由五个相同的小正方体组成的几何体,它的俯视图是( )
A. B. C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】D
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上面看易得底层是两个正方形,上层是两个正方形,类似于应该“田”字.
故选:D.
【点评】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
2.(2025 大同模拟)如图是由5个相同小立方体搭成的几何体,若将小立方体①放到小立方体②的正上方,则关于该几何体变化前后的三视图,下列说法正确的是( )
A.主视图不变,左视图、俯视图改变
B.左视图、俯视图不变,主视图改变
C.主视图、俯视图不变,左视图改变
D.主视图、俯视图、左视图都发生改变
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据三视图的定义求解即可.
【解答】解:根据图形可知,组合后的几何体左视图、俯视图不变,主视图改变.
故选:B.
【点评】本题考查了简单组合体的三视图,掌握几何体的结构是关键.
3.(2025 青阳县模拟)如图,两个大小不同的球在水平面上紧紧靠在一起,其俯视图是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】C
【分析】找到从上面看所得到的图形即可.
【解答】解:从上面看,可得选项C的图形.
故选:C.
【点评】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
4.(2025 宁陵县三模)“斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据俯视图是从上面看到的图形进行求解即可.
【解答】解:从上面看,看到的图形为一个正方形,在这个正方形里面还有一个小正方形,即看到的图形为,
故选C.
【点评】本题主要考查了简单几何体的三视图,熟知俯视图是从上面看到的图形是解题的关键.
5.(2025 南阳模拟)榫卯是我国传统建筑及家具的基本构件.燕尾榫是“万榫之母”,为了防止受拉力时脱开,榫头成梯台形,形似燕尾.如图是燕尾榫的带榫头部分,它的主视图是( )
A. B. C. D.
【考点】简单几何体的三视图.
【专题】投影与视图;几何直观.
【答案】A
【分析】正面看到的平面图形是主视图,根据主视图的定义可得答案.
【解答】解:这个几何体的主视图如下:
.
故选:A.
【点评】本题考查简单组合体的三视图,理解视图的定义,掌握简单组合体三视图的画法是正确解答的关键.
6.(2025 普宁市一模)如图所示是皮影戏,它是中国民间古老的传统艺术.皮影戏是用灯光把人物剪影照射在银幕上,则它的投影属于( )
A.平行投影
B.中心投影
C.既是平行投影又是中心投影
D.无法确定
【考点】中心投影;平行投影.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据由太阳光形成的投影是平行投影、由灯光形成的投影是中心投影判断即可.
【解答】解:由题意可得:它的投影属于中心投影.
故选B.
【点评】本题考查了中心投影和平行投影的知识,正确记忆相关知识点是解题关键.
7.(2025 高新区校级模拟)“陀螺”一词的正式出现是在明朝时期,打陀螺是一项深受各民族群众喜爱的体育运动.如图是一个水平放置的木陀螺(上面是圆柱体,下面是圆锥体)玩具,它的主视图是( )
A. B. C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】A
【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中,看不到的棱需要用虚线来表示.
【解答】解:从正面看易得,底层是一个三角形,上层是一个矩形,
故选:A.
【点评】本题主要考查了三视图的知识,主视图是从物体的正面看得到的视图,掌握主视图的概念是解题的关键.
8.(2025 大洼区校级三模)作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.如图是一把做工精湛的紫砂壶“景舟石瓢”,下面四幅图是从上面看到的图形的是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据俯视图的定义,从上面看所得到的图形即为俯视图.
【解答】解:根据视图的定义,选项B中的图形符合题意,
故选:B.
【点评】本题考查简单组合体的三视图,理解视图的定义是正确判断的前提.
9.(2025 东莞市校级模拟)用一个平面截长方体,得到如图的几何体,它在我国古代数学名著《九章算术》中被称为“堑堵”.“堑堵”的俯视图是( )
A. B.
C. D.
【考点】简单组合体的三视图;截一个几何体.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据从上面看得到的图形是俯视图,可得答案.
【解答】解:“堑堵”的俯视图是一个矩形,
故选:C.
【点评】本题考查了简单几何体的三视图,从上面看得到的图形是俯视图.
10.(2025 章丘区二模)我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的左视图是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据从左边看到的平面图形即可求解.
【解答】解:由几何体的左视图为:
故选:B.
【点评】本题考查了物体的三视图,掌握物体三视图的画法是解题的关键.
二.填空题(共5小题)
11.(2025 崆峒区校级一模)如图,从三个不同方向看同一个几何体得到的平面图形,则这个几何体的表面积是 cm .
【考点】由三视图判断几何体;几何体的表面积.
【专题】投影与视图;空间观念;运算能力.
【答案】见试题解答内容
【分析】利用三视图可得出几何体的形状,再利用已知各棱长得出这个几何体的侧面积.
【解答】解:这个几何体是直三棱柱,
4×3×3=36(cm2).
故这个几何体的侧面积是36cm2.
两个底面的面积之和为:24(cm2),
∴这个几何体的表面积是cm2.
故答案为:cm2.
【点评】此题主要考查了由三视图判断几何体以及几何体的表面积,正确得出物体的形状是解题关键.
12.(2025 天河区校级三模)如图所示是某几何体的三视图,根据图中数据计算,这个几何体侧面展开图的圆心角的度数为 120 °.
【考点】由三视图判断几何体;几何体的展开图.
【专题】与圆有关的计算;投影与视图;运算能力.
【答案】120.
【分析】由常见几何体的三视图可得该几何体为圆锥,根据三视图知圆锥的底面圆的直径为4、半径为2,高为4,得出母线长为6,再根据扇形的弧长公式可得答案.
【解答】解:由三视图可知,该几何体为圆锥;
由三视图数据知圆锥的底面圆的直径为4、半径为2,高为4,
则母线长为6,
所以该几何体的侧面展开图圆心角的度数为π×4÷(π×6)×180°=120°.
故答案为:120.
【点评】本题主要考查由三视图判断几何体,解题的关键是掌握常见几何体的三视图及扇形的弧长计算.
13.(2025 苏州校级二模)某三棱柱的三视图如图所示,其中主视图和左视图为矩形,俯视图为△ABC,已知,∠C=45°,则左视图的面积是 2 .
【考点】由三视图判断几何体;解直角三角形;简单几何体的三视图.
【专题】解直角三角形及其应用;投影与视图;空间观念;运算能力.
【答案】2.
【分析】根据这个几何体的三视图,得出这个三棱柱,高为2,BC=4,设CD=m,由,求出m的值,进而确定AD=1,即可解答.
【解答】解:过点A作AD⊥BC,由简图可知,这个几何体是三棱柱,高为2,BC=4,设CD=m,
由条件可知AD=CD=m,
∵,BD=4﹣m,
∴,
解得m=1,即AD=1,
则1×2=2,
∴左视图长方形的长为2,宽为1,所以左视图的面积是2.
故答案为:2.
【点评】本题考查简单几何体的三视图,理解视图的定义,掌握简单几何体三视图的形状是正确解答的前提.
14.(2025 兴庆区校级一模)如图,一块面积为60cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1,若OB:BB1=2:3,则△A1B1C1的面积为 375 .
【考点】中心投影;三角形的面积.
【专题】三角形;投影与视图;运算能力.
【答案】375.
【分析】△ABC与△A1B1C1是位似图形,求出位似比,再根据面积比等于位似比的平方即可求解.
【解答】解:∵OB:BB1=2:3,
∴OB:OB1=2:5,
∴△ABC与△A1B1C1的位似比为2:5,
∴,
∴,
故答案为:375.
【点评】本题考查平行投影,熟练掌握该知识点是关键.
15.(2025 肃南县校级一模)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”(图①)的形状示意图.是⊙O的一部分,D是的中点,连接OD,与弦AB交于点C,连接OA,OB.已知AB=24cm,碗深CD=8cm,则⊙O的半径OA为 13cm
【考点】由三视图判断几何体;垂径定理的应用;简单组合体的三视图.
【专题】投影与视图;运算能力.
【答案】13cm.
【分析】设⊙O的半径OA为Rcm,列出关于R的方程是解题的关键.首先利用垂径定理的推论得出OD⊥AB,,再设⊙O的半径OA为Rcm,则OC=(R﹣8)cm.在Rt△OAC中根据勾股定理列出方程R2=122+(R﹣8)2,求出R即可.
【解答】解:∵是⊙O的一部分,D是的中点,AB=24cm,
∴OD⊥AB,.
设⊙O的半径OA为Rcm,则OC=OD﹣CD=(R﹣8)cm.
在Rt△OAC中,∵∠OCA=90°,
∴OA2=AC2+OC2,
∴R2=122+(R﹣8)2,
∴R=13,
即⊙O的半径OA为13cm.
故答案为:13cm.
【点评】本题考查了垂径定理、勾股定理的应用,熟记垂径定理是解题的关键.
三.解答题(共5小题)
16.(2025 南京模拟)【综合与实践】南京文化纪念品的包装优化
南京作为历史文化名城,有众多特色文化纪念品.某纪念品生产厂家在20周年厂庆前,为其经典的“南京云锦”主题纪念品设计了长方体包装盒.但在实际生产与使用中发现,装入纪念品后包装盒边角空余空间较多,造成了包装材料的浪费,于是决定开展节省材料的探究活动.
任务1 平面图形的探究
南京的传统建筑中常常能看到矩形的窗户等元素.对于面积固定的矩形,我们来探究其周长的变化规律.已知秦淮河畔某古建筑修复时用到的一种矩形装饰砖面积为36平方分米,通过列举不同长和宽的情况,得到以下表格:
长(分米) 36 18 12 9 6
宽(分米) 1 2 3 4 5
周长(分米) 74 40 30 26 24
根据表格,可猜测:矩形的面积一定时, 长和宽相等 时周长最小.
为了证明上述猜测,小宁同学假设矩形面积为n2(n>0),设两邻边长分别为n﹣s和n+t(s,t均为非负数),则(n﹣s)(n+t)=n2,经化简可得,请表示出周长并补全后续的证明过程.
任务2 立体图形的包装改进
厂家之前设计的长方体包装盒尺寸为:长10厘米、宽8厘米、高6厘米,该包装盒用于包装以南京明城墙为原型的小型纪念品.现打算在保持底面积不变的前提下,将包装盒形状改为底面半径为4厘米的圆柱体,高保持不变,从节省材料(即表面积最小)的角度来看,你觉得这样的改进合理吗?请判断并说明理由.(取3.14,结果精确到0.1平方厘米)
【考点】简单组合体的三视图;近似数和有效数字;多项式乘多项式;几何体的表面积;三角形三边关系;圆柱的计算.
【专题】整式;与圆有关的计算;投影与视图;运算能力.
【答案】任务1:长和宽相等;,证明见解析;
任务2:这样的改进合理,理由见解析.
【分析】任务1:根据矩形周长计算公式可得矩形的周长为,则当s=t=0时,矩形的周长有最小值,即矩形的面积一定时,矩形的长和宽相等时周长最小;
任务2:分别计算长方体和圆柱的表面积,比较即可得到结论.
【解答】解:任务1:由条件可知矩形的周长为2(n﹣s+n+t)=4n+2(t﹣s),
∵,
∴矩形的周长为,
∵n为定值,
∴当st有最小值时,矩形的周长有最小值,
∴当s=t=0时,矩形的周长有最小值,
∴矩形的面积一定时,矩形的长和宽相等时周长最小;
(2)合理,理由如下:
长方体的表面积为2×(10×8+10×6+8×6)=376平方厘米,
圆柱的表面积为2×3.14×4×4+2×3.14×4×6=251.2平方厘米,
∴这样的改进合理.
【点评】本题主要考查了多项式乘法在几何图形中的应用,圆柱和长方体的表面积计算,正确理解题意是解题的关键.
17.(2025 连城县模拟)综合与实践
问题情境 学校准备在一面高2m、宽4m的墙上建一扇拱形门,这面墙的主视图为矩形ABCD,如图1.老师让同学们帮忙设计,要求既美观大方,又尽可能地容易通过.
方案设计 A小组设计的是半圆形拱门,如图2,以AB为直径的半圆O与矩形ABCD三边都相切.
B小组设计的是抛物线形拱门,如图3,抛物线的顶点P在墙的上沿CD的中点处,且抛物线过点A和点B.
提出问题 A,B两小组设计的拱门哪个“通过性”更好呢?
分析问题 老师建议同学们分别计算它们的“内接正方形”(正方形的两个顶点在线段AB上,两个顶点在半圆或抛物线上)面积的大小,通过比较两种设计方案的“内接正方形”的面积,判断它们的“通过性”.
解决问题 请你先分别画出两种方案的“内接正方形”的示意图,然后分别计算它们的面积,并利用计算结果说明哪个方案的拱门“通过性”更好.()
【考点】由三视图判断几何体;二次函数的应用;切线的性质;简单几何体的三视图.
【专题】二次函数图象及其性质;二次函数的应用;矩形 菱形 正方形;解直角三角形及其应用;运算能力;推理能力.
【答案】图2中正方形的“通过性”较大.
【分析】根据正方形的性质以及勾股定理求出图2中正方形的边长,在图3中建立直角坐标系,求出抛物线的关系式,再根据抛物线的对称性、正方形的性质以及二次函数图象上点的坐标特征求出正方形的边长,比较图2、图3中正方形的边长的大小即可.
【解答】解:如图2,由对称性可知,OM=ONPM,OA=OBAB=2,
设OM=x m,则PM=2x m,
在Rt△POM中,由勾股定理得,
OM2+PM2=OP2,
即x2+(2x)2=22,
解得x (取正值),
∴正方形的边长为MN=2OM1.8(m),
如图3,建立如图所示坐标系,则点A(﹣2,0),点B(2,0),顶点P(0,2),
设抛物线的关系式为y=ax2+bx+c,由题意得,
,
解得,
∴抛物线的关系式为yx2+2,
设ON=k,则QNk2+2=2k,
解得k2(取正值),
∴正方形的边长为44≈1.7(m),
∴图2中正方形的“通过性”较大.
【点评】本题考查二次函数图象上点的坐标特征,正方形的性质以及简单几何体的三视图,掌握二次函数图象上点的坐标特征,正方形的性质以及简单几何体的三视图的画法是正确解答的关键.
18.(2025 永寿县校级模拟)春夏之交,正适合去山野间漫游,蓝天白云下,青山绿水间,择一处草地,支一顶帐篷,邀亲朋好友,闻清风,话家常,好不惬意.一款帐篷的支架简单,携带方便,适合一般的休闲旅行使用,它的形状可近似看作抛物线,该款帐篷在搭建时,张开的宽度和顶部高度会影响容纳的椅子数量,如图①是该款帐篷搭建完成的平面示意图,其张开的宽度AB=2m,顶部高度MN=1.2m,现以点A为坐标原点,AB所在直线为x轴,过点A且平行于MN的直线为y轴建立平面直角坐标系.
(1)求该帐篷支架对应的抛物线的表达式;
(2)如图②为一把椅子摆入该帐篷后的简易视图,椅子高度EC=0.9m,宽度CD=0.3m,若在该帐篷内沿AB方向摆放一排此款椅子,则最多可摆放多少把椅子?
【考点】由三视图判断几何体;二次函数的应用.
【专题】二次函数的应用;运算能力.
【答案】(1)y=﹣1.2x2+2.4x;
(2)3.
【分析】(1)根据题意得出点A(0,0),点B(2,0),顶点M(1,1.2),再利用待定系数法求出抛物线的关系式即可;
(2)求出当y=0.9时对应的两个x的值,再根据两个x之间的距离以及椅子的宽度和高度进行计算即可.
【解答】解:(1)由题意可知,点A(0,0),点B(2,0),顶点M(1,1.2),
设抛物线的表达式为y=ax2+bx+c,则,
,
解得,
∴该帐篷支架对应的抛物线的表达式y=﹣1.2x2+2.4x;
(2)由题意得,
当y=0.9时,即﹣1.2x2+2.4x=0.9,
解得x=0.5或x=1.5,
又∵CD=0.3m,1.5﹣0.5=1m,而1÷0.3=3……0.1,
∴在该帐篷内沿AB方向摆放一排此款椅子最多可摆放3把椅子.
【点评】本题考查二次函数的应用,掌握待定系数法求二次函数的关系式是正确解答的关键.
19.(2025 淮安区校级一模)图1是一个不倒翁模型,图2是它的主视图,由△ABC和以O为圆心的弧组成,已知OC⊥AB,AD=BD=24cm,OD=18cm,CD=32cm.
(1)求证:AC是⊙O的切线;
(2)如图3,转动模型使AC与地面EF平行,求此时点B到地面的距离BF的长度.
【考点】由三视图判断几何体;勾股定理的应用;切线的判定与性质.
【专题】与圆有关的位置关系;图形的相似;运算能力;推理能力.
【答案】(1)见解答;(2)21.6.
【分析】(1)连接OA.证△ADO∽△CDA,得∠OAD=∠ACD,据此可知∠ACD+∠AOD=∠OAD+∠AOD=90°,从而得证;
(2)接OB,延长FB交AC于点H,由AC∥EF,∠BFE=90°知∠BHC=∠BFE=90°,结合,cm,cm,则,得BH的长度,继而可得答案.
【解答】解:(1)连接OA.
Rt△ADO与Rt△CDA中,∵∠ADO=∠CDA=90°,,
∴△ADO∽△CDA,
∴∠OAD=∠ACD,
∴∠ACD+∠AOD=∠OAD+∠AOD=90°,即∠OAC=90°,
∴OA⊥AC,
又∵OA是⊙O半径,
∴AC是⊙O的切线.
(2)连接OB,延长FB交AC于点H,
∵AC∥EF,∠BFE=90°,
∴∠BHC=∠BFE=90°,
∵S△ABC,AO30(cm),AC40cm,
∴,BH=38.4cm,
∴BF=FH﹣BH=60﹣38.4=21.6(cm).
【点评】本题主要考查相似三角形的判定与性质、切线的判定与性质,解题的关键是掌握切线的判定与性质.
20.(2025 安阳县二模)某设计师结合数学知识设计了一款沙发,沙发的三视图如图1所示,将沙发侧面示意图简化后,得到图2所示图形.为了解沙发的相关性能,设计师将图形放入平面直角坐标系中,其中曲线AB是反比例函数的一段图象,线段BD是一次函数的一段图象,点B的坐标为(25,40),沙发腿DE⊥x轴,BC与x轴交于点C.请你根据图形解决以下问题:
(1)请求出反比例函数和一次函数的表达式;(不要求写x的取值范围)
(2)过点A向x轴作垂线,交x轴于点F.已知CF=7cm,CE=33cm,DE=45cm,设计师想用一个长方体箱子将沙发放进去,则这个长方体箱子的长、宽、高至少分别是多少?
【考点】由三视图判断几何体;反比例函数的应用.
【专题】投影与视图;运算能力.
【答案】(1),;(2)长方体箱子的长、宽、高至少分别是60cm,40cm,100cm.
【分析】(1)将点B(25,40)代入,即可得出反比例函数表达式;将点B(25,40)代入,即可得出一次函数表达式;
(2)把y=45代入,得出D(50,45),进而得出点F的坐标为(10,0),将x=10代入,得出点A的坐标为(10,100),继而分析得出长方体箱子的长、宽、高.
【解答】解:(1)由条件可得k=25×40=1000,
∴反比例函数表达式为,
将点B(25,40)代入,得,
解得b=35,
∴一次函数表达式为;
(2)把y=45代入,得x=50,
∴D(50,45),即OE=50cm,
∵CF=7cm,CE=33cm,
∴EF=CF+CE=40(cm),OF=OE﹣CF﹣CE=10(cm),
∴点F的坐标为(10,0),
将x=10代入,得y=100,
∴点A的坐标为(10,100),
∴AF=100cm,
根据图1可知,沙发的长是60cm.
综上,长方体箱子的长、宽、高至少分别是60cm,40cm,100cm.
【点评】本题考查了简单几何体的三视图,反比例函数的应用,掌握几何体的空间结构是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年中考数学一轮复习 投影与视图
一.选择题(共10小题)
1.(2025 武汉)如图是由五个相同的小正方体组成的几何体,它的俯视图是( )
A. B. C. D.
2.(2025 大同模拟)如图是由5个相同小立方体搭成的几何体,若将小立方体①放到小立方体②的正上方,则关于该几何体变化前后的三视图,下列说法正确的是( )
A.主视图不变,左视图、俯视图改变
B.左视图、俯视图不变,主视图改变
C.主视图、俯视图不变,左视图改变
D.主视图、俯视图、左视图都发生改变
3.(2025 青阳县模拟)如图,两个大小不同的球在水平面上紧紧靠在一起,其俯视图是( )
A. B.
C. D.
4.(2025 宁陵县三模)“斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )
A. B.
C. D.
5.(2025 南阳模拟)榫卯是我国传统建筑及家具的基本构件.燕尾榫是“万榫之母”,为了防止受拉力时脱开,榫头成梯台形,形似燕尾.如图是燕尾榫的带榫头部分,它的主视图是( )
A. B. C. D.
6.(2025 普宁市一模)如图所示是皮影戏,它是中国民间古老的传统艺术.皮影戏是用灯光把人物剪影照射在银幕上,则它的投影属于( )
A.平行投影
B.中心投影
C.既是平行投影又是中心投影
D.无法确定
7.(2025 高新区校级模拟)“陀螺”一词的正式出现是在明朝时期,打陀螺是一项深受各民族群众喜爱的体育运动.如图是一个水平放置的木陀螺(上面是圆柱体,下面是圆锥体)玩具,它的主视图是( )
A. B. C. D.
8.(2025 大洼区校级三模)作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.如图是一把做工精湛的紫砂壶“景舟石瓢”,下面四幅图是从上面看到的图形的是( )
A. B.
C. D.
9.(2025 东莞市校级模拟)用一个平面截长方体,得到如图的几何体,它在我国古代数学名著《九章算术》中被称为“堑堵”.“堑堵”的俯视图是( )
A. B.
C. D.
10.(2025 章丘区二模)我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的左视图是( )
A. B.
C. D.
二.填空题(共5小题)
11.(2025 崆峒区校级一模)如图,从三个不同方向看同一个几何体得到的平面图形,则这个几何体的表面积是 .
12.(2025 天河区校级三模)如图所示是某几何体的三视图,根据图中数据计算,这个几何体侧面展开图的圆心角的度数为 °.
13.(2025 苏州校级二模)某三棱柱的三视图如图所示,其中主视图和左视图为矩形,俯视图为△ABC,已知,∠C=45°,则左视图的面积是 .
14.(2025 兴庆区校级一模)如图,一块面积为60cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1,若OB:BB1=2:3,则△A1B1C1的面积为 .
15.(2025 肃南县校级一模)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”(图①)的形状示意图.是⊙O的一部分,D是的中点,连接OD,与弦AB交于点C,连接OA,OB.已知AB=24cm,碗深CD=8cm,则⊙O的半径OA为
三.解答题(共5小题)
16.(2025 南京模拟)【综合与实践】南京文化纪念品的包装优化
南京作为历史文化名城,有众多特色文化纪念品.某纪念品生产厂家在20周年厂庆前,为其经典的“南京云锦”主题纪念品设计了长方体包装盒.但在实际生产与使用中发现,装入纪念品后包装盒边角空余空间较多,造成了包装材料的浪费,于是决定开展节省材料的探究活动.
任务1 平面图形的探究
南京的传统建筑中常常能看到矩形的窗户等元素.对于面积固定的矩形,我们来探究其周长的变化规律.已知秦淮河畔某古建筑修复时用到的一种矩形装饰砖面积为36平方分米,通过列举不同长和宽的情况,得到以下表格:
长(分米) 36 18 12 9 6
宽(分米) 1 2 3 4 5
周长(分米) 74 40 30 26 24
根据表格,可猜测:矩形的面积一定时, 时周长最小.
为了证明上述猜测,小宁同学假设矩形面积为n2(n>0),设两邻边长分别为n﹣s和n+t(s,t均为非负数),则(n﹣s)(n+t)=n2,经化简可得,请表示出周长并补全后续的证明过程.
任务2 立体图形的包装改进
厂家之前设计的长方体包装盒尺寸为:长10厘米、宽8厘米、高6厘米,该包装盒用于包装以南京明城墙为原型的小型纪念品.现打算在保持底面积不变的前提下,将包装盒形状改为底面半径为4厘米的圆柱体,高保持不变,从节省材料(即表面积最小)的角度来看,你觉得这样的改进合理吗?请判断并说明理由.(取3.14,结果精确到0.1平方厘米)
17.(2025 连城县模拟)综合与实践
问题情境 学校准备在一面高2m、宽4m的墙上建一扇拱形门,这面墙的主视图为矩形ABCD,如图1.老师让同学们帮忙设计,要求既美观大方,又尽可能地容易通过.
方案设计 A小组设计的是半圆形拱门,如图2,以AB为直径的半圆O与矩形ABCD三边都相切.
B小组设计的是抛物线形拱门,如图3,抛物线的顶点P在墙的上沿CD的中点处,且抛物线过点A和点B.
提出问题 A,B两小组设计的拱门哪个“通过性”更好呢?
分析问题 老师建议同学们分别计算它们的“内接正方形”(正方形的两个顶点在线段AB上,两个顶点在半圆或抛物线上)面积的大小,通过比较两种设计方案的“内接正方形”的面积,判断它们的“通过性”.
解决问题 请你先分别画出两种方案的“内接正方形”的示意图,然后分别计算它们的面积,并利用计算结果说明哪个方案的拱门“通过性”更好.()
18.(2025 永寿县校级模拟)春夏之交,正适合去山野间漫游,蓝天白云下,青山绿水间,择一处草地,支一顶帐篷,邀亲朋好友,闻清风,话家常,好不惬意.一款帐篷的支架简单,携带方便,适合一般的休闲旅行使用,它的形状可近似看作抛物线,该款帐篷在搭建时,张开的宽度和顶部高度会影响容纳的椅子数量,如图①是该款帐篷搭建完成的平面示意图,其张开的宽度AB=2m,顶部高度MN=1.2m,现以点A为坐标原点,AB所在直线为x轴,过点A且平行于MN的直线为y轴建立平面直角坐标系.
(1)求该帐篷支架对应的抛物线的表达式;
(2)如图②为一把椅子摆入该帐篷后的简易视图,椅子高度EC=0.9m,宽度CD=0.3m,若在该帐篷内沿AB方向摆放一排此款椅子,则最多可摆放多少把椅子?
19.(2025 淮安区校级一模)图1是一个不倒翁模型,图2是它的主视图,由△ABC和以O为圆心的弧组成,已知OC⊥AB,AD=BD=24cm,OD=18cm,CD=32cm.
(1)求证:AC是⊙O的切线;
(2)如图3,转动模型使AC与地面EF平行,求此时点B到地面的距离BF的长度.
20.(2025 安阳县二模)某设计师结合数学知识设计了一款沙发,沙发的三视图如图1所示,将沙发侧面示意图简化后,得到图2所示图形.为了解沙发的相关性能,设计师将图形放入平面直角坐标系中,其中曲线AB是反比例函数的一段图象,线段BD是一次函数的一段图象,点B的坐标为(25,40),沙发腿DE⊥x轴,BC与x轴交于点C.请你根据图形解决以下问题:
(1)请求出反比例函数和一次函数的表达式;(不要求写x的取值范围)
(2)过点A向x轴作垂线,交x轴于点F.已知CF=7cm,CE=33cm,DE=45cm,设计师想用一个长方体箱子将沙发放进去,则这个长方体箱子的长、宽、高至少分别是多少?
2026年中考数学一轮复习 投影与视图
参考答案与试题解析
一.选择题(共10小题)
1.(2025 武汉)如图是由五个相同的小正方体组成的几何体,它的俯视图是( )
A. B. C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】D
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上面看易得底层是两个正方形,上层是两个正方形,类似于应该“田”字.
故选:D.
【点评】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
2.(2025 大同模拟)如图是由5个相同小立方体搭成的几何体,若将小立方体①放到小立方体②的正上方,则关于该几何体变化前后的三视图,下列说法正确的是( )
A.主视图不变,左视图、俯视图改变
B.左视图、俯视图不变,主视图改变
C.主视图、俯视图不变,左视图改变
D.主视图、俯视图、左视图都发生改变
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据三视图的定义求解即可.
【解答】解:根据图形可知,组合后的几何体左视图、俯视图不变,主视图改变.
故选:B.
【点评】本题考查了简单组合体的三视图,掌握几何体的结构是关键.
3.(2025 青阳县模拟)如图,两个大小不同的球在水平面上紧紧靠在一起,其俯视图是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】C
【分析】找到从上面看所得到的图形即可.
【解答】解:从上面看,可得选项C的图形.
故选:C.
【点评】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
4.(2025 宁陵县三模)“斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据俯视图是从上面看到的图形进行求解即可.
【解答】解:从上面看,看到的图形为一个正方形,在这个正方形里面还有一个小正方形,即看到的图形为,
故选C.
【点评】本题主要考查了简单几何体的三视图,熟知俯视图是从上面看到的图形是解题的关键.
5.(2025 南阳模拟)榫卯是我国传统建筑及家具的基本构件.燕尾榫是“万榫之母”,为了防止受拉力时脱开,榫头成梯台形,形似燕尾.如图是燕尾榫的带榫头部分,它的主视图是( )
A. B. C. D.
【考点】简单几何体的三视图.
【专题】投影与视图;几何直观.
【答案】A
【分析】正面看到的平面图形是主视图,根据主视图的定义可得答案.
【解答】解:这个几何体的主视图如下:
.
故选:A.
【点评】本题考查简单组合体的三视图,理解视图的定义,掌握简单组合体三视图的画法是正确解答的关键.
6.(2025 普宁市一模)如图所示是皮影戏,它是中国民间古老的传统艺术.皮影戏是用灯光把人物剪影照射在银幕上,则它的投影属于( )
A.平行投影
B.中心投影
C.既是平行投影又是中心投影
D.无法确定
【考点】中心投影;平行投影.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据由太阳光形成的投影是平行投影、由灯光形成的投影是中心投影判断即可.
【解答】解:由题意可得:它的投影属于中心投影.
故选B.
【点评】本题考查了中心投影和平行投影的知识,正确记忆相关知识点是解题关键.
7.(2025 高新区校级模拟)“陀螺”一词的正式出现是在明朝时期,打陀螺是一项深受各民族群众喜爱的体育运动.如图是一个水平放置的木陀螺(上面是圆柱体,下面是圆锥体)玩具,它的主视图是( )
A. B. C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】A
【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中,看不到的棱需要用虚线来表示.
【解答】解:从正面看易得,底层是一个三角形,上层是一个矩形,
故选:A.
【点评】本题主要考查了三视图的知识,主视图是从物体的正面看得到的视图,掌握主视图的概念是解题的关键.
8.(2025 大洼区校级三模)作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.如图是一把做工精湛的紫砂壶“景舟石瓢”,下面四幅图是从上面看到的图形的是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据俯视图的定义,从上面看所得到的图形即为俯视图.
【解答】解:根据视图的定义,选项B中的图形符合题意,
故选:B.
【点评】本题考查简单组合体的三视图,理解视图的定义是正确判断的前提.
9.(2025 东莞市校级模拟)用一个平面截长方体,得到如图的几何体,它在我国古代数学名著《九章算术》中被称为“堑堵”.“堑堵”的俯视图是( )
A. B.
C. D.
【考点】简单组合体的三视图;截一个几何体.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据从上面看得到的图形是俯视图,可得答案.
【解答】解:“堑堵”的俯视图是一个矩形,
故选:C.
【点评】本题考查了简单几何体的三视图,从上面看得到的图形是俯视图.
10.(2025 章丘区二模)我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的左视图是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据从左边看到的平面图形即可求解.
【解答】解:由几何体的左视图为:
故选:B.
【点评】本题考查了物体的三视图,掌握物体三视图的画法是解题的关键.
二.填空题(共5小题)
11.(2025 崆峒区校级一模)如图,从三个不同方向看同一个几何体得到的平面图形,则这个几何体的表面积是 cm .
【考点】由三视图判断几何体;几何体的表面积.
【专题】投影与视图;空间观念;运算能力.
【答案】见试题解答内容
【分析】利用三视图可得出几何体的形状,再利用已知各棱长得出这个几何体的侧面积.
【解答】解:这个几何体是直三棱柱,
4×3×3=36(cm2).
故这个几何体的侧面积是36cm2.
两个底面的面积之和为:24(cm2),
∴这个几何体的表面积是cm2.
故答案为:cm2.
【点评】此题主要考查了由三视图判断几何体以及几何体的表面积,正确得出物体的形状是解题关键.
12.(2025 天河区校级三模)如图所示是某几何体的三视图,根据图中数据计算,这个几何体侧面展开图的圆心角的度数为 120 °.
【考点】由三视图判断几何体;几何体的展开图.
【专题】与圆有关的计算;投影与视图;运算能力.
【答案】120.
【分析】由常见几何体的三视图可得该几何体为圆锥,根据三视图知圆锥的底面圆的直径为4、半径为2,高为4,得出母线长为6,再根据扇形的弧长公式可得答案.
【解答】解:由三视图可知,该几何体为圆锥;
由三视图数据知圆锥的底面圆的直径为4、半径为2,高为4,
则母线长为6,
所以该几何体的侧面展开图圆心角的度数为π×4÷(π×6)×180°=120°.
故答案为:120.
【点评】本题主要考查由三视图判断几何体,解题的关键是掌握常见几何体的三视图及扇形的弧长计算.
13.(2025 苏州校级二模)某三棱柱的三视图如图所示,其中主视图和左视图为矩形,俯视图为△ABC,已知,∠C=45°,则左视图的面积是 2 .
【考点】由三视图判断几何体;解直角三角形;简单几何体的三视图.
【专题】解直角三角形及其应用;投影与视图;空间观念;运算能力.
【答案】2.
【分析】根据这个几何体的三视图,得出这个三棱柱,高为2,BC=4,设CD=m,由,求出m的值,进而确定AD=1,即可解答.
【解答】解:过点A作AD⊥BC,由简图可知,这个几何体是三棱柱,高为2,BC=4,设CD=m,
由条件可知AD=CD=m,
∵,BD=4﹣m,
∴,
解得m=1,即AD=1,
则1×2=2,
∴左视图长方形的长为2,宽为1,所以左视图的面积是2.
故答案为:2.
【点评】本题考查简单几何体的三视图,理解视图的定义,掌握简单几何体三视图的形状是正确解答的前提.
14.(2025 兴庆区校级一模)如图,一块面积为60cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1,若OB:BB1=2:3,则△A1B1C1的面积为 375 .
【考点】中心投影;三角形的面积.
【专题】三角形;投影与视图;运算能力.
【答案】375.
【分析】△ABC与△A1B1C1是位似图形,求出位似比,再根据面积比等于位似比的平方即可求解.
【解答】解:∵OB:BB1=2:3,
∴OB:OB1=2:5,
∴△ABC与△A1B1C1的位似比为2:5,
∴,
∴,
故答案为:375.
【点评】本题考查平行投影,熟练掌握该知识点是关键.
15.(2025 肃南县校级一模)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”(图①)的形状示意图.是⊙O的一部分,D是的中点,连接OD,与弦AB交于点C,连接OA,OB.已知AB=24cm,碗深CD=8cm,则⊙O的半径OA为 13cm
【考点】由三视图判断几何体;垂径定理的应用;简单组合体的三视图.
【专题】投影与视图;运算能力.
【答案】13cm.
【分析】设⊙O的半径OA为Rcm,列出关于R的方程是解题的关键.首先利用垂径定理的推论得出OD⊥AB,,再设⊙O的半径OA为Rcm,则OC=(R﹣8)cm.在Rt△OAC中根据勾股定理列出方程R2=122+(R﹣8)2,求出R即可.
【解答】解:∵是⊙O的一部分,D是的中点,AB=24cm,
∴OD⊥AB,.
设⊙O的半径OA为Rcm,则OC=OD﹣CD=(R﹣8)cm.
在Rt△OAC中,∵∠OCA=90°,
∴OA2=AC2+OC2,
∴R2=122+(R﹣8)2,
∴R=13,
即⊙O的半径OA为13cm.
故答案为:13cm.
【点评】本题考查了垂径定理、勾股定理的应用,熟记垂径定理是解题的关键.
三.解答题(共5小题)
16.(2025 南京模拟)【综合与实践】南京文化纪念品的包装优化
南京作为历史文化名城,有众多特色文化纪念品.某纪念品生产厂家在20周年厂庆前,为其经典的“南京云锦”主题纪念品设计了长方体包装盒.但在实际生产与使用中发现,装入纪念品后包装盒边角空余空间较多,造成了包装材料的浪费,于是决定开展节省材料的探究活动.
任务1 平面图形的探究
南京的传统建筑中常常能看到矩形的窗户等元素.对于面积固定的矩形,我们来探究其周长的变化规律.已知秦淮河畔某古建筑修复时用到的一种矩形装饰砖面积为36平方分米,通过列举不同长和宽的情况,得到以下表格:
长(分米) 36 18 12 9 6
宽(分米) 1 2 3 4 5
周长(分米) 74 40 30 26 24
根据表格,可猜测:矩形的面积一定时, 长和宽相等 时周长最小.
为了证明上述猜测,小宁同学假设矩形面积为n2(n>0),设两邻边长分别为n﹣s和n+t(s,t均为非负数),则(n﹣s)(n+t)=n2,经化简可得,请表示出周长并补全后续的证明过程.
任务2 立体图形的包装改进
厂家之前设计的长方体包装盒尺寸为:长10厘米、宽8厘米、高6厘米,该包装盒用于包装以南京明城墙为原型的小型纪念品.现打算在保持底面积不变的前提下,将包装盒形状改为底面半径为4厘米的圆柱体,高保持不变,从节省材料(即表面积最小)的角度来看,你觉得这样的改进合理吗?请判断并说明理由.(取3.14,结果精确到0.1平方厘米)
【考点】简单组合体的三视图;近似数和有效数字;多项式乘多项式;几何体的表面积;三角形三边关系;圆柱的计算.
【专题】整式;与圆有关的计算;投影与视图;运算能力.
【答案】任务1:长和宽相等;,证明见解析;
任务2:这样的改进合理,理由见解析.
【分析】任务1:根据矩形周长计算公式可得矩形的周长为,则当s=t=0时,矩形的周长有最小值,即矩形的面积一定时,矩形的长和宽相等时周长最小;
任务2:分别计算长方体和圆柱的表面积,比较即可得到结论.
【解答】解:任务1:由条件可知矩形的周长为2(n﹣s+n+t)=4n+2(t﹣s),
∵,
∴矩形的周长为,
∵n为定值,
∴当st有最小值时,矩形的周长有最小值,
∴当s=t=0时,矩形的周长有最小值,
∴矩形的面积一定时,矩形的长和宽相等时周长最小;
(2)合理,理由如下:
长方体的表面积为2×(10×8+10×6+8×6)=376平方厘米,
圆柱的表面积为2×3.14×4×4+2×3.14×4×6=251.2平方厘米,
∴这样的改进合理.
【点评】本题主要考查了多项式乘法在几何图形中的应用,圆柱和长方体的表面积计算,正确理解题意是解题的关键.
17.(2025 连城县模拟)综合与实践
问题情境 学校准备在一面高2m、宽4m的墙上建一扇拱形门,这面墙的主视图为矩形ABCD,如图1.老师让同学们帮忙设计,要求既美观大方,又尽可能地容易通过.
方案设计 A小组设计的是半圆形拱门,如图2,以AB为直径的半圆O与矩形ABCD三边都相切.
B小组设计的是抛物线形拱门,如图3,抛物线的顶点P在墙的上沿CD的中点处,且抛物线过点A和点B.
提出问题 A,B两小组设计的拱门哪个“通过性”更好呢?
分析问题 老师建议同学们分别计算它们的“内接正方形”(正方形的两个顶点在线段AB上,两个顶点在半圆或抛物线上)面积的大小,通过比较两种设计方案的“内接正方形”的面积,判断它们的“通过性”.
解决问题 请你先分别画出两种方案的“内接正方形”的示意图,然后分别计算它们的面积,并利用计算结果说明哪个方案的拱门“通过性”更好.()
【考点】由三视图判断几何体;二次函数的应用;切线的性质;简单几何体的三视图.
【专题】二次函数图象及其性质;二次函数的应用;矩形 菱形 正方形;解直角三角形及其应用;运算能力;推理能力.
【答案】图2中正方形的“通过性”较大.
【分析】根据正方形的性质以及勾股定理求出图2中正方形的边长,在图3中建立直角坐标系,求出抛物线的关系式,再根据抛物线的对称性、正方形的性质以及二次函数图象上点的坐标特征求出正方形的边长,比较图2、图3中正方形的边长的大小即可.
【解答】解:如图2,由对称性可知,OM=ONPM,OA=OBAB=2,
设OM=x m,则PM=2x m,
在Rt△POM中,由勾股定理得,
OM2+PM2=OP2,
即x2+(2x)2=22,
解得x (取正值),
∴正方形的边长为MN=2OM1.8(m),
如图3,建立如图所示坐标系,则点A(﹣2,0),点B(2,0),顶点P(0,2),
设抛物线的关系式为y=ax2+bx+c,由题意得,
,
解得,
∴抛物线的关系式为yx2+2,
设ON=k,则QNk2+2=2k,
解得k2(取正值),
∴正方形的边长为44≈1.7(m),
∴图2中正方形的“通过性”较大.
【点评】本题考查二次函数图象上点的坐标特征,正方形的性质以及简单几何体的三视图,掌握二次函数图象上点的坐标特征,正方形的性质以及简单几何体的三视图的画法是正确解答的关键.
18.(2025 永寿县校级模拟)春夏之交,正适合去山野间漫游,蓝天白云下,青山绿水间,择一处草地,支一顶帐篷,邀亲朋好友,闻清风,话家常,好不惬意.一款帐篷的支架简单,携带方便,适合一般的休闲旅行使用,它的形状可近似看作抛物线,该款帐篷在搭建时,张开的宽度和顶部高度会影响容纳的椅子数量,如图①是该款帐篷搭建完成的平面示意图,其张开的宽度AB=2m,顶部高度MN=1.2m,现以点A为坐标原点,AB所在直线为x轴,过点A且平行于MN的直线为y轴建立平面直角坐标系.
(1)求该帐篷支架对应的抛物线的表达式;
(2)如图②为一把椅子摆入该帐篷后的简易视图,椅子高度EC=0.9m,宽度CD=0.3m,若在该帐篷内沿AB方向摆放一排此款椅子,则最多可摆放多少把椅子?
【考点】由三视图判断几何体;二次函数的应用.
【专题】二次函数的应用;运算能力.
【答案】(1)y=﹣1.2x2+2.4x;
(2)3.
【分析】(1)根据题意得出点A(0,0),点B(2,0),顶点M(1,1.2),再利用待定系数法求出抛物线的关系式即可;
(2)求出当y=0.9时对应的两个x的值,再根据两个x之间的距离以及椅子的宽度和高度进行计算即可.
【解答】解:(1)由题意可知,点A(0,0),点B(2,0),顶点M(1,1.2),
设抛物线的表达式为y=ax2+bx+c,则,
,
解得,
∴该帐篷支架对应的抛物线的表达式y=﹣1.2x2+2.4x;
(2)由题意得,
当y=0.9时,即﹣1.2x2+2.4x=0.9,
解得x=0.5或x=1.5,
又∵CD=0.3m,1.5﹣0.5=1m,而1÷0.3=3……0.1,
∴在该帐篷内沿AB方向摆放一排此款椅子最多可摆放3把椅子.
【点评】本题考查二次函数的应用,掌握待定系数法求二次函数的关系式是正确解答的关键.
19.(2025 淮安区校级一模)图1是一个不倒翁模型,图2是它的主视图,由△ABC和以O为圆心的弧组成,已知OC⊥AB,AD=BD=24cm,OD=18cm,CD=32cm.
(1)求证:AC是⊙O的切线;
(2)如图3,转动模型使AC与地面EF平行,求此时点B到地面的距离BF的长度.
【考点】由三视图判断几何体;勾股定理的应用;切线的判定与性质.
【专题】与圆有关的位置关系;图形的相似;运算能力;推理能力.
【答案】(1)见解答;(2)21.6.
【分析】(1)连接OA.证△ADO∽△CDA,得∠OAD=∠ACD,据此可知∠ACD+∠AOD=∠OAD+∠AOD=90°,从而得证;
(2)接OB,延长FB交AC于点H,由AC∥EF,∠BFE=90°知∠BHC=∠BFE=90°,结合,cm,cm,则,得BH的长度,继而可得答案.
【解答】解:(1)连接OA.
Rt△ADO与Rt△CDA中,∵∠ADO=∠CDA=90°,,
∴△ADO∽△CDA,
∴∠OAD=∠ACD,
∴∠ACD+∠AOD=∠OAD+∠AOD=90°,即∠OAC=90°,
∴OA⊥AC,
又∵OA是⊙O半径,
∴AC是⊙O的切线.
(2)连接OB,延长FB交AC于点H,
∵AC∥EF,∠BFE=90°,
∴∠BHC=∠BFE=90°,
∵S△ABC,AO30(cm),AC40cm,
∴,BH=38.4cm,
∴BF=FH﹣BH=60﹣38.4=21.6(cm).
【点评】本题主要考查相似三角形的判定与性质、切线的判定与性质,解题的关键是掌握切线的判定与性质.
20.(2025 安阳县二模)某设计师结合数学知识设计了一款沙发,沙发的三视图如图1所示,将沙发侧面示意图简化后,得到图2所示图形.为了解沙发的相关性能,设计师将图形放入平面直角坐标系中,其中曲线AB是反比例函数的一段图象,线段BD是一次函数的一段图象,点B的坐标为(25,40),沙发腿DE⊥x轴,BC与x轴交于点C.请你根据图形解决以下问题:
(1)请求出反比例函数和一次函数的表达式;(不要求写x的取值范围)
(2)过点A向x轴作垂线,交x轴于点F.已知CF=7cm,CE=33cm,DE=45cm,设计师想用一个长方体箱子将沙发放进去,则这个长方体箱子的长、宽、高至少分别是多少?
【考点】由三视图判断几何体;反比例函数的应用.
【专题】投影与视图;运算能力.
【答案】(1),;(2)长方体箱子的长、宽、高至少分别是60cm,40cm,100cm.
【分析】(1)将点B(25,40)代入,即可得出反比例函数表达式;将点B(25,40)代入,即可得出一次函数表达式;
(2)把y=45代入,得出D(50,45),进而得出点F的坐标为(10,0),将x=10代入,得出点A的坐标为(10,100),继而分析得出长方体箱子的长、宽、高.
【解答】解:(1)由条件可得k=25×40=1000,
∴反比例函数表达式为,
将点B(25,40)代入,得,
解得b=35,
∴一次函数表达式为;
(2)把y=45代入,得x=50,
∴D(50,45),即OE=50cm,
∵CF=7cm,CE=33cm,
∴EF=CF+CE=40(cm),OF=OE﹣CF﹣CE=10(cm),
∴点F的坐标为(10,0),
将x=10代入,得y=100,
∴点A的坐标为(10,100),
∴AF=100cm,
根据图1可知,沙发的长是60cm.
综上,长方体箱子的长、宽、高至少分别是60cm,40cm,100cm.
【点评】本题考查了简单几何体的三视图,反比例函数的应用,掌握几何体的空间结构是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
