2026年中考数学一轮复习 图形的平移(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 图形的平移(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 04:30:48 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2026年中考数学一轮复习 图形的平移
一.选择题(共10小题)
1.(2025 红花岗区校级模拟)甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )
A. B. C. D.
2.(2025 威海模拟)点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8) B.(1,﹣2) C.(﹣6,﹣1) D.(0,﹣1)
3.(2025 东方二模)点P(8,3)向上平移6个单位长度,下列说法正确的是( )
A.点P的横坐标加6,纵坐标不变
B.点P的纵坐标加6,横坐标不变
C.点P的横坐标减6,纵坐标不变
D.点P的纵坐标减6,横坐标不变
4.(2025 石家庄二模)如图,在Rt△ABC中,∠C=90°,AC=BC=6,将Rt△ABC沿着射线BA方向平移得到Rt△A′B′C′,当点C′落在∠ABC的平分线上时,B′C′交AC于点E,此时CE的长为( )
A.4 B.5 C. D.
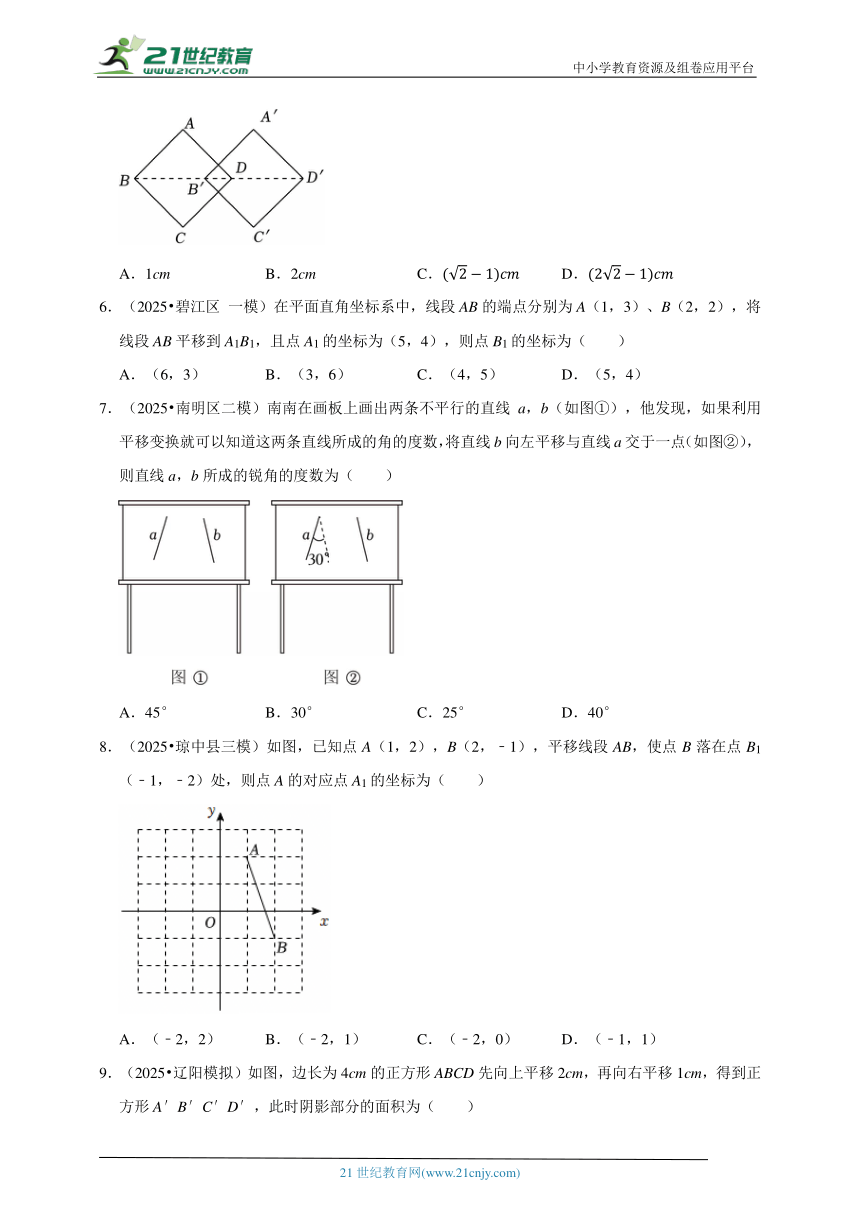
5.(2025 白山模拟)“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥,如图,将边长为1cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A.1cm B.2cm C. D.
6.(2025 碧江区 一模)在平面直角坐标系中,线段AB的端点分别为A(1,3)、B(2,2),将线段AB平移到A1B1,且点A1的坐标为(5,4),则点B1的坐标为( )
A.(6,3) B.(3,6) C.(4,5) D.(5,4)
7.(2025 南明区二模)南南在画板上画出两条不平行的直线a,b(如图①),他发现,如果利用平移变换就可以知道这两条直线所成的角的度数,将直线b向左平移与直线a交于一点(如图②),则直线a,b所成的锐角的度数为( )
A.45° B.30° C.25° D.40°
8.(2025 琼中县三模)如图,已知点A(1,2),B(2,﹣1),平移线段AB,使点B落在点B1(﹣1,﹣2)处,则点A的对应点A1的坐标为( )
A.(﹣2,2) B.(﹣2,1) C.(﹣2,0) D.(﹣1,1)
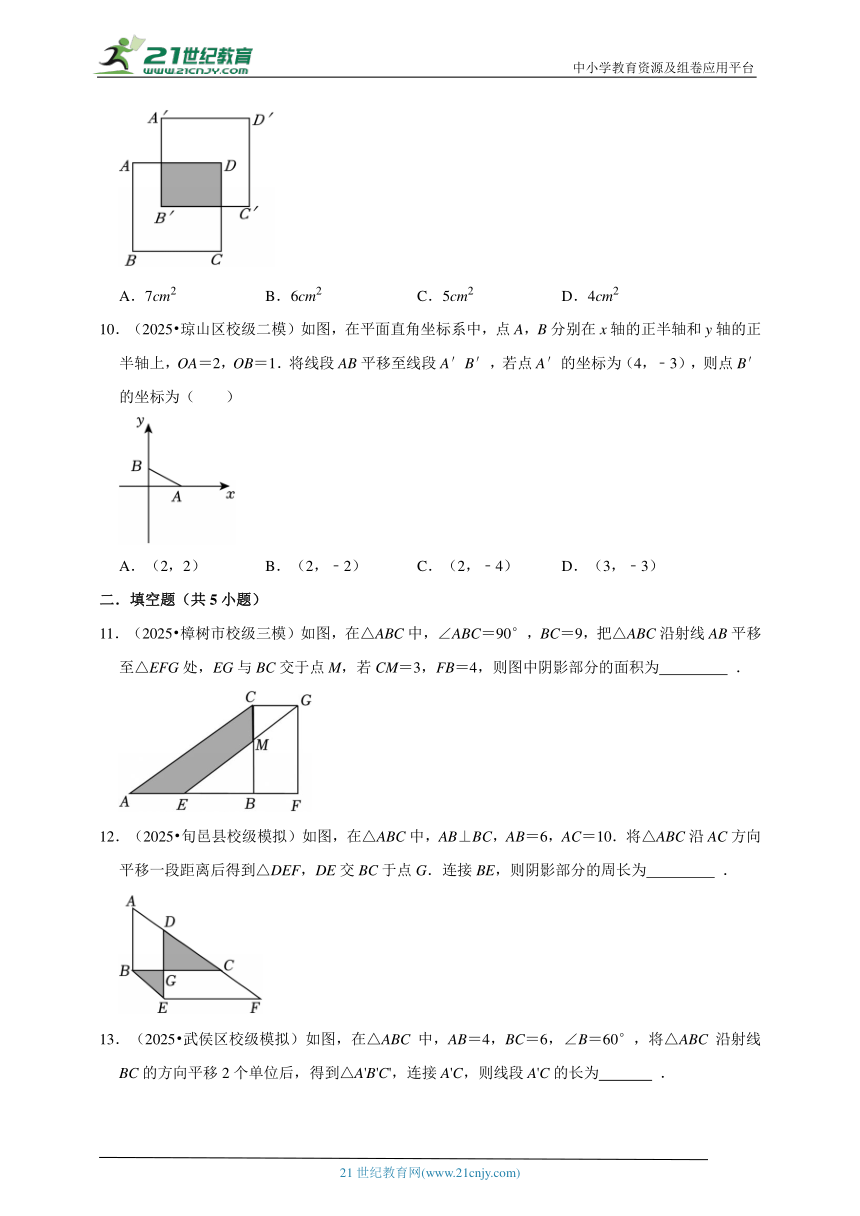
9.(2025 辽阳模拟)如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为( )
A.7cm2 B.6cm2 C.5cm2 D.4cm2
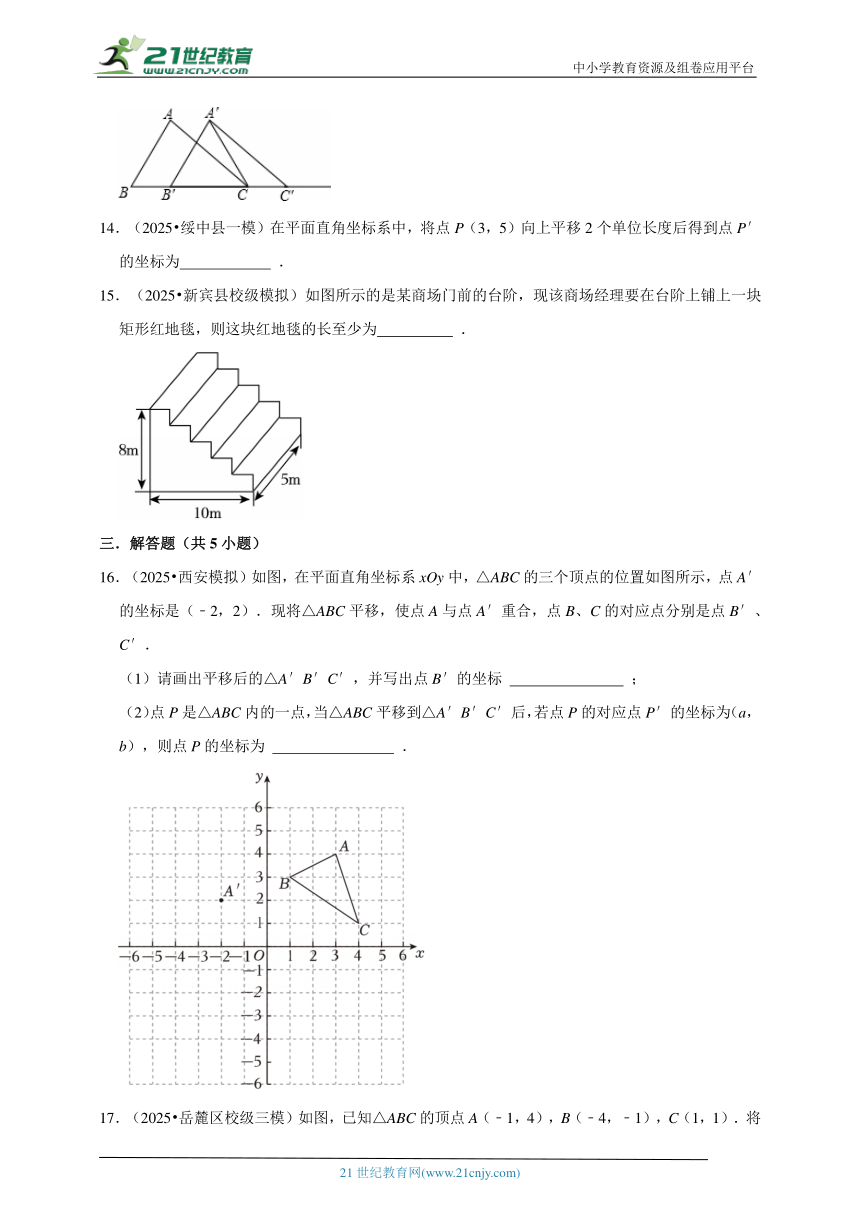
10.(2025 琼山区校级二模)如图,在平面直角坐标系中,点A,B分别在x轴的正半轴和y轴的正半轴上,OA=2,OB=1.将线段AB平移至线段A′B′,若点A′的坐标为(4,﹣3),则点B′的坐标为( )
A.(2,2) B.(2,﹣2) C.(2,﹣4) D.(3,﹣3)
二.填空题(共5小题)
11.(2025 樟树市校级三模)如图,在△ABC中,∠ABC=90°,BC=9,把△ABC沿射线AB平移至△EFG处,EG与BC交于点M,若CM=3,FB=4,则图中阴影部分的面积为 .
12.(2025 旬邑县校级模拟)如图,在△ABC中,AB⊥BC,AB=6,AC=10.将△ABC沿AC方向平移一段距离后得到△DEF,DE交BC于点G.连接BE,则阴影部分的周长为 .
13.(2025 武侯区校级模拟)如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A'B'C',连接A'C,则线段A'C的长为 .
14.(2025 绥中县一模)在平面直角坐标系中,将点P(3,5)向上平移2个单位长度后得到点P′的坐标为 .
15.(2025 新宾县校级模拟)如图所示的是某商场门前的台阶,现该商场经理要在台阶上铺上一块矩形红地毯,则这块红地毯的长至少为 .
三.解答题(共5小题)
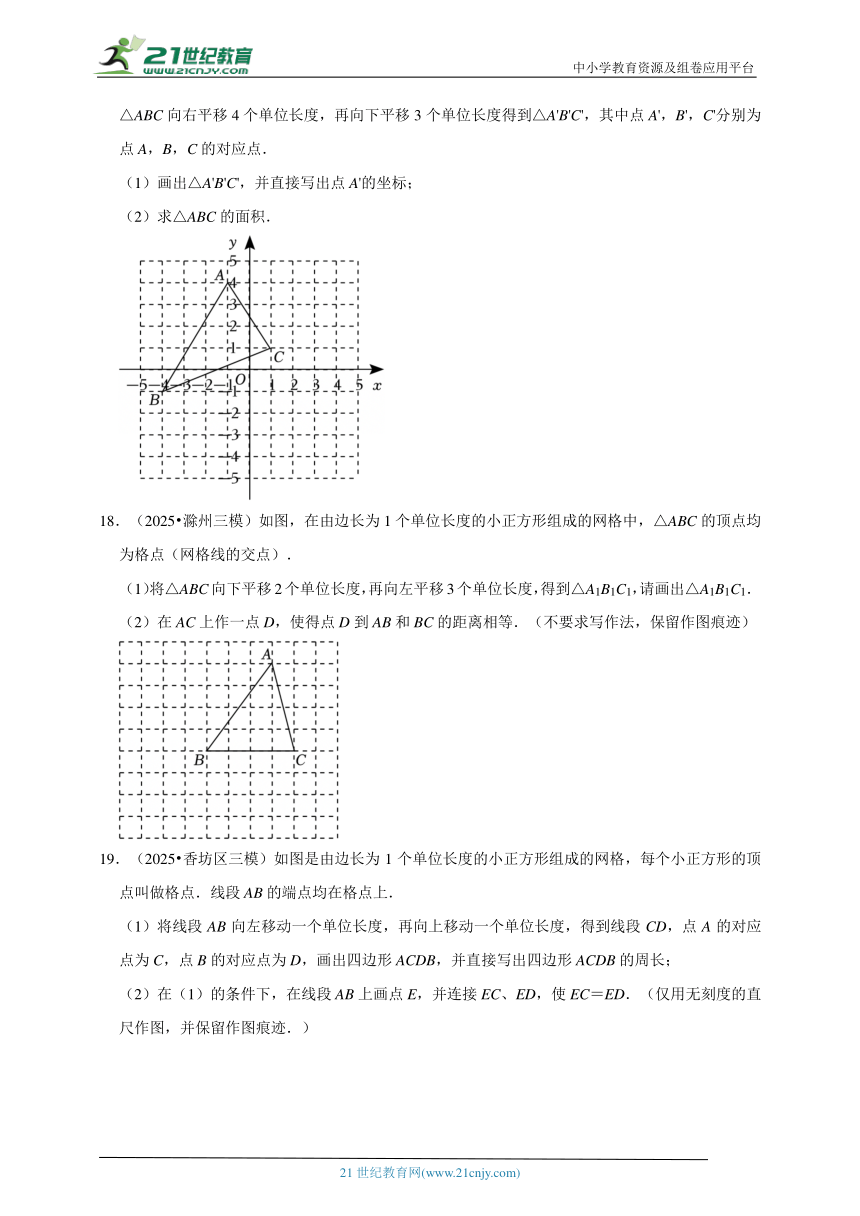
16.(2025 西安模拟)如图,在平面直角坐标系xOy中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2).现将△ABC平移,使点A与点A′重合,点B、C的对应点分别是点B′、C′.
(1)请画出平移后的△A′B′C′,并写出点B′的坐标 ;
(2)点P是△ABC内的一点,当△ABC平移到△A′B′C′后,若点P的对应点P′的坐标为(a,b),则点P的坐标为 .
17.(2025 岳麓区校级三模)如图,已知△ABC的顶点A(﹣1,4),B(﹣4,﹣1),C(1,1).将△ABC向右平移4个单位长度,再向下平移3个单位长度得到△A'B'C',其中点A',B',C'分别为点A,B,C的对应点.
(1)画出△A'B'C',并直接写出点A'的坐标;
(2)求△ABC的面积.
18.(2025 滁州三模)如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).
(1)将△ABC向下平移2个单位长度,再向左平移3个单位长度,得到△A1B1C1,请画出△A1B1C1.
(2)在AC上作一点D,使得点D到AB和BC的距离相等.(不要求写作法,保留作图痕迹)
19.(2025 香坊区三模)如图是由边长为1个单位长度的小正方形组成的网格,每个小正方形的顶点叫做格点.线段AB的端点均在格点上.
(1)将线段AB向左移动一个单位长度,再向上移动一个单位长度,得到线段CD,点A的对应点为C,点B的对应点为D,画出四边形ACDB,并直接写出四边形ACDB的周长;
(2)在(1)的条件下,在线段AB上画点E,并连接EC、ED,使EC=ED.(仅用无刻度的直尺作图,并保留作图痕迹.)
20.(2025 武汉模拟)如图是由小正方形组成的7×4网格,每个小正方形的顶点叫做格点.平行四边形ABCD四个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.
(1)在图(1)中,点E是边AD上一点,在线段ED上画一点F,使得DF=AE;
(2)在(1)的基础上,将BE平移到CG,画出线段CG.
(3)在图(2)中,平行四边形对角线的交点为O,在AD上画一点H,使得HB=HD,连接BH;
(4)在(3)的基础上,将BH绕着O点顺时针旋转∠AHB的度数得到线段MN,点M与点B对应,点N与点H对应,画出线段MN.
2026年中考数学一轮复习 图形的平移
参考答案与试题解析
一.选择题(共10小题)
1.(2025 红花岗区校级模拟)甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )
A. B. C. D.
【考点】生活中的平移现象.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】根据图形平移的性质解答即可.
【解答】解:由图可知A是平移得到,B、C,D不是平移得到,
故选:A.
【点评】本题考查的是利用平移设计图案,熟知图形平移不变性的性质是解答此题的关键.
2.(2025 威海模拟)点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8) B.(1,﹣2) C.(﹣6,﹣1) D.(0,﹣1)
【考点】坐标与图形变化﹣平移.
【专题】动点型.
【答案】C
【分析】直接利用平移中点的变化规律求解即可.
【解答】解:点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位得到点B,坐标变化为(﹣3﹣3,﹣5+4);则点B的坐标为(﹣6,﹣1).
故选:C.
【点评】本题考查点坐标的平移变换.关键是要懂得左右平移点的纵坐标不变,而上下平移时点的横坐标不变.平移中,对应点的对应坐标的差相等.
3.(2025 东方二模)点P(8,3)向上平移6个单位长度,下列说法正确的是( )
A.点P的横坐标加6,纵坐标不变
B.点P的纵坐标加6,横坐标不变
C.点P的横坐标减6,纵坐标不变
D.点P的纵坐标减6,横坐标不变
【考点】坐标与图形变化﹣平移.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】根据平移时点的坐标变化规律即可解决问题.
【解答】解:由题知,
将点P(8,3)向上平移6个单位长度后,
点P的横坐标不变,纵坐标增加6,
显然只有B选项符合题意.
故选:B.
【点评】本题主要考查了坐标与图形变化﹣平移,熟知平移时点的坐标变化规律是解题的关键.
4.(2025 石家庄二模)如图,在Rt△ABC中,∠C=90°,AC=BC=6,将Rt△ABC沿着射线BA方向平移得到Rt△A′B′C′,当点C′落在∠ABC的平分线上时,B′C′交AC于点E,此时CE的长为( )
A.4 B.5 C. D.
【考点】平移的性质;角平分线的性质;勾股定理;等腰直角三角形.
【专题】等腰三角形与直角三角形;运算能力.
【答案】C
【分析】根据平移的性质,得出△BB′C′为等腰三角形及△AB′E为等腰直角三角形,求出AE的长,据此可解决问题.
【解答】解:由平移可知,
BC∥B′C′,B′C′=BC=6,
∴∠CBC′=∠BC′B′.
又∵BC′平分∠CBB′,
∴∠CBC′=∠B′BC′,
∴∠B′BC′=∠BC′B′,
∴BB′=B′C′=6.
∵AB,
∴AB′,
∴AE,
∴CE=AC﹣AE=6﹣().
故选:C.
【点评】本题主要考查了平移的性质、角平分线的性质、勾股定理及等腰直角三角形,熟知平移的性质及等腰直角三角形的性质是解题的关键.
5.(2025 白山模拟)“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥,如图,将边长为1cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A.1cm B.2cm C. D.
【考点】利用平移设计图案;全等图形.
【专题】推理能力.
【答案】C
【分析】根据正方形的性质、勾股定理求出BD,根据平移的概念求出BB′,计算即可.
【解答】解:∵四边形ABCD是边长为1cm的正方形,
∴BD(cm),
由平移的性质可知BB′=1cm,
∴.
故选:C.
【点评】本题考查的是平移的性质、正方形的性质,勾股定理,根据平移的概念求出BB′是解题的关键.
6.(2025 碧江区 一模)在平面直角坐标系中,线段AB的端点分别为A(1,3)、B(2,2),将线段AB平移到A1B1,且点A1的坐标为(5,4),则点B1的坐标为( )
A.(6,3) B.(3,6) C.(4,5) D.(5,4)
【考点】坐标与图形变化﹣平移.
【专题】平面直角坐标系;符号意识.
【答案】A
【分析】根据点A的坐标平移后所得点的坐标得到平移规律,再根据平移规律可得点B的坐标.
【解答】解:B(2,2)向右平移4个单位,向上平移一个单位得到B1(6,3),
故选:A.
【点评】本题考查了坐标与图形变化﹣平移,确定平移规律是解题的关键.
7.(2025 南明区二模)南南在画板上画出两条不平行的直线a,b(如图①),他发现,如果利用平移变换就可以知道这两条直线所成的角的度数,将直线b向左平移与直线a交于一点(如图②),则直线a,b所成的锐角的度数为( )
A.45° B.30° C.25° D.40°
【考点】平移的性质.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】根据平移的性质即可解决问题.
【解答】解:由题知,
∵直线c由直线b平移得到,
∴c∥b.
又∵直线a与直线c所成锐角的度数为30°,
∴直线a,b所成锐角的度数为30°.
故选:B.
【点评】本题主要考查了平移的性质,熟知平移的性质是解题的关键.
8.(2025 琼中县三模)如图,已知点A(1,2),B(2,﹣1),平移线段AB,使点B落在点B1(﹣1,﹣2)处,则点A的对应点A1的坐标为( )
A.(﹣2,2) B.(﹣2,1) C.(﹣2,0) D.(﹣1,1)
【考点】坐标与图形变化﹣平移.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】由点B的坐标得出平移的方式,再根据平移的方式得出A点平移后的点的坐标即可.
【解答】解:∵点A(1,2),B(2,﹣1),平移线段AB,点B落在点B1(﹣1,﹣2)处,
∴AB先向下移动1个单位,再向左移动3个单位,
∵A(1,2),
∴A′(1﹣3,2﹣1),即A′(﹣2,1),
故选:B.
【点评】本题主要考查了坐标与图形变化﹣平移,熟知横坐标,右移加,左移减;纵坐标,上移加,下移减是解题的关键.
9.(2025 辽阳模拟)如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为( )
A.7cm2 B.6cm2 C.5cm2 D.4cm2
【考点】平移的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;推理能力.
【答案】B
【分析】由平移的性质可得A'E=2cm,AE=1cm,可求B'E=2cm,DE=3cm,即可求解.
【解答】解:如图,设AD与A'B'交于点E,
∵将边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,
∴A'E=2cm,AE=1cm,
∴B'E=2cm,DE=3cm,
∴阴影部分的面积=2×3=6cm2,
故选:B.
【点评】本题考查了正方形的性质,平移的性质,掌握平移的性质是解题的关键.
10.(2025 琼山区校级二模)如图,在平面直角坐标系中,点A,B分别在x轴的正半轴和y轴的正半轴上,OA=2,OB=1.将线段AB平移至线段A′B′,若点A′的坐标为(4,﹣3),则点B′的坐标为( )
A.(2,2) B.(2,﹣2) C.(2,﹣4) D.(3,﹣3)
【考点】坐标与图形变化﹣平移.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】根据题意,求出点A和点B的坐标,再结合点A和其对应点A′的坐标得出平移的方向和距离即可解决问题.
【解答】解:由题知,
因为OA=2,OB=1,
所以点A坐标为(2,0),点B坐标为(0,1).
又因为平移后点A的对应点A′的坐标为(4,﹣3),
则4﹣2=2,﹣3﹣0=﹣3,
所以0+2=2,1﹣3=﹣2,
所以点B′的坐标为(2,﹣2).
故选:B.
【点评】本题主要考查了坐标与图形变化﹣平移,熟知平移时点的坐标变化规律是解题的关键.
二.填空题(共5小题)
11.(2025 樟树市校级三模)如图,在△ABC中,∠ABC=90°,BC=9,把△ABC沿射线AB平移至△EFG处,EG与BC交于点M,若CM=3,FB=4,则图中阴影部分的面积为 30 .
【考点】平移的性质.
【专题】平移、旋转与对称;推理能力.
【答案】30.
【分析】利用平移的性质得到FG=BC=9,△ABC≌△EFG,则S△ABC=S△EFG,所以S四边形AEMC=S梯形BFGM,然后根据梯形的面积公式计算.
【解答】解:∵△AB沿射线AB方向平移至△EFG,
∴FG=BC=9,△ABC≌△EFG,
∴S△ABC=S△EFG,BM=BC﹣CM=9﹣3=6,
即S四边形AEMC+S△EBM=S△EBM+S梯形BFGM,
∴S四边形AEMC=S梯形BFGM(6+9)×4=30.
故答案为:30.
【点评】本题考查了平移的性质:把求图中阴影部分的面积转化求为梯形BFGM的面积是解决问题的关键.
12.(2025 旬邑县校级模拟)如图,在△ABC中,AB⊥BC,AB=6,AC=10.将△ABC沿AC方向平移一段距离后得到△DEF,DE交BC于点G.连接BE,则阴影部分的周长为 24 .
【考点】平移的性质.
【专题】平移、旋转与对称;推理能力.
【答案】24.
【分析】根据勾股定理求出BC=8,根据平移的性质求出BE=AD,AB=DE,再根据周长定义求解即可.
【解答】解:∵AB⊥BC,AB=6,AC=10,
∴,
由平移的性质可得,BE=AD,AB=DE,
∴阴影部分的周长为BE+BC+DE+CD=AD+BC+AB+CD,
∵AC=AD+CD,
∴阴影部分的周长为BC+AB+AC=8+6+10=24,
故答案为:24.
【点评】此题考查了平移的性质,熟记平移的性质是解题的关键.
13.(2025 武侯区校级模拟)如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A'B'C',连接A'C,则线段A'C的长为 4 .
【考点】平移的性质.
【专题】等腰三角形与直角三角形;几何直观.
【答案】4.
【分析】根据平移性质,判定△A′B′C为等边三角形,然后求解.
【解答】解:由题意,得BB′=2,
∴B′C=BC﹣BB′=4.
由平移性质,可知A′B′=AB=4,∠A′B′C=∠ABC=60°,
∴A′B′=B′C,且∠A′B′C=60°,
∴△A′B′C为等边三角形,
∴A'C=A'B'=4,
故答案为:4.
【点评】本题考查的是平移的性质,熟知图形平移后新图形与原图形的形状和大小完全相同是解答此题的关键.
14.(2025 绥中县一模)在平面直角坐标系中,将点P(3,5)向上平移2个单位长度后得到点P′的坐标为 (3,7) .
【考点】坐标与图形变化﹣平移.
【专题】平面直角坐标系;平移、旋转与对称;几何直观.
【答案】(3,7).
【分析】根据点的坐标平移规则:左减右加,上加下减求解即可.
【解答】解:根据点的坐标平移规则:左减右加,上加下减可得点P′的坐标为(3,5+2),即(3,7),
故答案为:(3,7).
【点评】本题考查坐标与图形变换﹣平移变换,熟练掌握该知识点是关键.
15.(2025 新宾县校级模拟)如图所示的是某商场门前的台阶,现该商场经理要在台阶上铺上一块矩形红地毯,则这块红地毯的长至少为 18m .
【考点】生活中的平移现象.
【专题】平移、旋转与对称;几何直观.
【答案】18m.
【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积即可.
【解答】解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为10米,8米,
故地毯的长度为8+10=18(米).
故答案为:18m.
【点评】此题考查了生活中的平移现象,掌握平移现象的特点是关键.
三.解答题(共5小题)
16.(2025 西安模拟)如图,在平面直角坐标系xOy中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2).现将△ABC平移,使点A与点A′重合,点B、C的对应点分别是点B′、C′.
(1)请画出平移后的△A′B′C′,并写出点B′的坐标 B′(﹣4,1) ;
(2)点P是△ABC内的一点,当△ABC平移到△A′B′C′后,若点P的对应点P′的坐标为(a,b),则点P的坐标为 (a+5,b+2) .
【考点】作图﹣平移变换.
【专题】作图题;几何直观.
【答案】(1)B′(﹣4,1),图见解析;
(2)点P的坐标为(a+5,b+2).
【分析】(1)先根据题意求出平移方向,从而求出B′,C′的坐标,画出图形即可;
(2)根据(1)中的平移方向,即可求解.
【解答】解:(1)∵点A′的坐标是(﹣2,2),点A的坐标是(3,4),
∴平移方向是先向右平移5个单位长度,再向下平移2个单位长度,
∵点B的坐标是(1,3),点C的坐标是(4,1),
∴点B′的坐标是(﹣4,1),点C′的坐标是(﹣1,﹣1),
∴平移后的△A′B′C′如图所示:
(2)由(1)得:平移方向是先向右平移5个单位长度,再向下平移2个单位长度,
∵点P的对应点P′的坐标为(a,b),
∴点P的坐标为(a+5,b+2);
【点评】本题主要考查了作图﹣平移变换,正确得出对应点位置是解题关键.
17.(2025 岳麓区校级三模)如图,已知△ABC的顶点A(﹣1,4),B(﹣4,﹣1),C(1,1).将△ABC向右平移4个单位长度,再向下平移3个单位长度得到△A'B'C',其中点A',B',C'分别为点A,B,C的对应点.
(1)画出△A'B'C',并直接写出点A'的坐标;
(2)求△ABC的面积.
【考点】作图﹣平移变换.
【专题】平移、旋转与对称;几何直观;运算能力.
【答案】(1)画图见解答;点A'的坐标为(3,1).
(2).
【分析】(1)根据平移的性质作图,即可得出答案.
(2)利用割补法求三角形的面积即可.
【解答】解:(1)如图,△A'B'C'即为所求.
由图可得,点A'的坐标为(3,1).
(2)△ABC的面积为.
【点评】本题考查作图﹣平移变换,熟练掌握平移的性质是解答本题的关键.
18.(2025 滁州三模)如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).
(1)将△ABC向下平移2个单位长度,再向左平移3个单位长度,得到△A1B1C1,请画出△A1B1C1.
(2)在AC上作一点D,使得点D到AB和BC的距离相等.(不要求写作法,保留作图痕迹)
【考点】作图﹣平移变换;角平分线的性质;等腰三角形的性质.
【专题】平移、旋转与对称;几何直观.
【答案】(1)见解答.
(2)见解答.
【分析】(1)根据平移的性质作图即可.
(2)结合等腰三角形的性质和角平分线的性质,在BC的延长线上取点E,使BE=AB,取AE的中点F,作射线BF交AC于点D,则点D即为所求.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,在BC的延长线上取点E,使BE=AB,取AE的中点F,作射线BF交AC于点D,
此时BD为∠ABC的平分线,
∴点D到AB和BC的距离相等,
则点D即为所求.
【点评】本题考查作图﹣平移变换、角平分线的性质、等腰三角形的性质,熟练掌握轴对称的性质、角平分线的性质、等腰三角形的性质是解答本题的关键.
19.(2025 香坊区三模)如图是由边长为1个单位长度的小正方形组成的网格,每个小正方形的顶点叫做格点.线段AB的端点均在格点上.
(1)将线段AB向左移动一个单位长度,再向上移动一个单位长度,得到线段CD,点A的对应点为C,点B的对应点为D,画出四边形ACDB,并直接写出四边形ACDB的周长;
(2)在(1)的条件下,在线段AB上画点E,并连接EC、ED,使EC=ED.(仅用无刻度的直尺作图,并保留作图痕迹.)
【考点】作图﹣平移变换;勾股定理.
【专题】平移、旋转与对称;空间观念;几何直观.
【答案】(1)画图见解答;.
(2)见解答.
【分析】(1)根据平移的性质作图即可;结合勾股定理计算即可.
(2)作线段CD的垂直平分线,交AB于点E,则点E即为所求.
【解答】解:(1)如图,四边形ACDB即为所求.
由勾股定理得AC=BD,AB=CD,
∴四边形ACDB的周长为AC+BD+AB+CD.
(2)如图,作线段CD的垂直平分线,交AB于点E,连接EC、ED,
则点E即为所求.
【点评】本题考查作图﹣平移变换、勾股定理,熟练掌握平移的性质、勾股定理是解答本题的关键.
20.(2025 武汉模拟)如图是由小正方形组成的7×4网格,每个小正方形的顶点叫做格点.平行四边形ABCD四个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.
(1)在图(1)中,点E是边AD上一点,在线段ED上画一点F,使得DF=AE;
(2)在(1)的基础上,将BE平移到CG,画出线段CG.
(3)在图(2)中,平行四边形对角线的交点为O,在AD上画一点H,使得HB=HD,连接BH;
(4)在(3)的基础上,将BH绕着O点顺时针旋转∠AHB的度数得到线段MN,点M与点B对应,点N与点H对应,画出线段MN.
【考点】作图﹣平移变换;旋转的性质;线段垂直平分线的性质;勾股定理;勾股定理的逆定理;平行四边形的性质.
【专题】作图题;几何直观.
【答案】见解析.
【分析】(1)延长BE交网格线于点J,取格点K,连接JK交AD于点F,点F即为所求;
(2)线段JK交网格线于点I,连接CI,延长CI交AD于点G,线段CG即为所求;
(3)取格点J,连接OJ交AD于点H,连接BH,点H即为所求;
(4)取格点M,P,连接OP交AD于点N,线段MN即为所求.
【解答】解:(1)如图1中,点F即为所求;
(2)如图1中,线段CG即为所求;
(3)如图2中,点H即为所求;
(4)如图2中,线段MN即为所求.
【点评】本题考查作图﹣平移后,线段的垂直平分线的性质,勾股定理,勾股定理的逆定理,平行四边形的性质,性质的性质,解题的关键是掌握相关知识解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年中考数学一轮复习 图形的平移
一.选择题(共10小题)
1.(2025 红花岗区校级模拟)甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )
A. B. C. D.
2.(2025 威海模拟)点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8) B.(1,﹣2) C.(﹣6,﹣1) D.(0,﹣1)
3.(2025 东方二模)点P(8,3)向上平移6个单位长度,下列说法正确的是( )
A.点P的横坐标加6,纵坐标不变
B.点P的纵坐标加6,横坐标不变
C.点P的横坐标减6,纵坐标不变
D.点P的纵坐标减6,横坐标不变
4.(2025 石家庄二模)如图,在Rt△ABC中,∠C=90°,AC=BC=6,将Rt△ABC沿着射线BA方向平移得到Rt△A′B′C′,当点C′落在∠ABC的平分线上时,B′C′交AC于点E,此时CE的长为( )
A.4 B.5 C. D.
5.(2025 白山模拟)“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥,如图,将边长为1cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A.1cm B.2cm C. D.
6.(2025 碧江区 一模)在平面直角坐标系中,线段AB的端点分别为A(1,3)、B(2,2),将线段AB平移到A1B1,且点A1的坐标为(5,4),则点B1的坐标为( )
A.(6,3) B.(3,6) C.(4,5) D.(5,4)
7.(2025 南明区二模)南南在画板上画出两条不平行的直线a,b(如图①),他发现,如果利用平移变换就可以知道这两条直线所成的角的度数,将直线b向左平移与直线a交于一点(如图②),则直线a,b所成的锐角的度数为( )
A.45° B.30° C.25° D.40°
8.(2025 琼中县三模)如图,已知点A(1,2),B(2,﹣1),平移线段AB,使点B落在点B1(﹣1,﹣2)处,则点A的对应点A1的坐标为( )
A.(﹣2,2) B.(﹣2,1) C.(﹣2,0) D.(﹣1,1)
9.(2025 辽阳模拟)如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为( )
A.7cm2 B.6cm2 C.5cm2 D.4cm2
10.(2025 琼山区校级二模)如图,在平面直角坐标系中,点A,B分别在x轴的正半轴和y轴的正半轴上,OA=2,OB=1.将线段AB平移至线段A′B′,若点A′的坐标为(4,﹣3),则点B′的坐标为( )
A.(2,2) B.(2,﹣2) C.(2,﹣4) D.(3,﹣3)
二.填空题(共5小题)
11.(2025 樟树市校级三模)如图,在△ABC中,∠ABC=90°,BC=9,把△ABC沿射线AB平移至△EFG处,EG与BC交于点M,若CM=3,FB=4,则图中阴影部分的面积为 .
12.(2025 旬邑县校级模拟)如图,在△ABC中,AB⊥BC,AB=6,AC=10.将△ABC沿AC方向平移一段距离后得到△DEF,DE交BC于点G.连接BE,则阴影部分的周长为 .
13.(2025 武侯区校级模拟)如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A'B'C',连接A'C,则线段A'C的长为 .
14.(2025 绥中县一模)在平面直角坐标系中,将点P(3,5)向上平移2个单位长度后得到点P′的坐标为 .
15.(2025 新宾县校级模拟)如图所示的是某商场门前的台阶,现该商场经理要在台阶上铺上一块矩形红地毯,则这块红地毯的长至少为 .
三.解答题(共5小题)
16.(2025 西安模拟)如图,在平面直角坐标系xOy中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2).现将△ABC平移,使点A与点A′重合,点B、C的对应点分别是点B′、C′.
(1)请画出平移后的△A′B′C′,并写出点B′的坐标 ;
(2)点P是△ABC内的一点,当△ABC平移到△A′B′C′后,若点P的对应点P′的坐标为(a,b),则点P的坐标为 .
17.(2025 岳麓区校级三模)如图,已知△ABC的顶点A(﹣1,4),B(﹣4,﹣1),C(1,1).将△ABC向右平移4个单位长度,再向下平移3个单位长度得到△A'B'C',其中点A',B',C'分别为点A,B,C的对应点.
(1)画出△A'B'C',并直接写出点A'的坐标;
(2)求△ABC的面积.
18.(2025 滁州三模)如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).
(1)将△ABC向下平移2个单位长度,再向左平移3个单位长度,得到△A1B1C1,请画出△A1B1C1.
(2)在AC上作一点D,使得点D到AB和BC的距离相等.(不要求写作法,保留作图痕迹)
19.(2025 香坊区三模)如图是由边长为1个单位长度的小正方形组成的网格,每个小正方形的顶点叫做格点.线段AB的端点均在格点上.
(1)将线段AB向左移动一个单位长度,再向上移动一个单位长度,得到线段CD,点A的对应点为C,点B的对应点为D,画出四边形ACDB,并直接写出四边形ACDB的周长;
(2)在(1)的条件下,在线段AB上画点E,并连接EC、ED,使EC=ED.(仅用无刻度的直尺作图,并保留作图痕迹.)
20.(2025 武汉模拟)如图是由小正方形组成的7×4网格,每个小正方形的顶点叫做格点.平行四边形ABCD四个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.
(1)在图(1)中,点E是边AD上一点,在线段ED上画一点F,使得DF=AE;
(2)在(1)的基础上,将BE平移到CG,画出线段CG.
(3)在图(2)中,平行四边形对角线的交点为O,在AD上画一点H,使得HB=HD,连接BH;
(4)在(3)的基础上,将BH绕着O点顺时针旋转∠AHB的度数得到线段MN,点M与点B对应,点N与点H对应,画出线段MN.
2026年中考数学一轮复习 图形的平移
参考答案与试题解析
一.选择题(共10小题)
1.(2025 红花岗区校级模拟)甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )
A. B. C. D.
【考点】生活中的平移现象.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】根据图形平移的性质解答即可.
【解答】解:由图可知A是平移得到,B、C,D不是平移得到,
故选:A.
【点评】本题考查的是利用平移设计图案,熟知图形平移不变性的性质是解答此题的关键.
2.(2025 威海模拟)点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8) B.(1,﹣2) C.(﹣6,﹣1) D.(0,﹣1)
【考点】坐标与图形变化﹣平移.
【专题】动点型.
【答案】C
【分析】直接利用平移中点的变化规律求解即可.
【解答】解:点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位得到点B,坐标变化为(﹣3﹣3,﹣5+4);则点B的坐标为(﹣6,﹣1).
故选:C.
【点评】本题考查点坐标的平移变换.关键是要懂得左右平移点的纵坐标不变,而上下平移时点的横坐标不变.平移中,对应点的对应坐标的差相等.
3.(2025 东方二模)点P(8,3)向上平移6个单位长度,下列说法正确的是( )
A.点P的横坐标加6,纵坐标不变
B.点P的纵坐标加6,横坐标不变
C.点P的横坐标减6,纵坐标不变
D.点P的纵坐标减6,横坐标不变
【考点】坐标与图形变化﹣平移.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】根据平移时点的坐标变化规律即可解决问题.
【解答】解:由题知,
将点P(8,3)向上平移6个单位长度后,
点P的横坐标不变,纵坐标增加6,
显然只有B选项符合题意.
故选:B.
【点评】本题主要考查了坐标与图形变化﹣平移,熟知平移时点的坐标变化规律是解题的关键.
4.(2025 石家庄二模)如图,在Rt△ABC中,∠C=90°,AC=BC=6,将Rt△ABC沿着射线BA方向平移得到Rt△A′B′C′,当点C′落在∠ABC的平分线上时,B′C′交AC于点E,此时CE的长为( )
A.4 B.5 C. D.
【考点】平移的性质;角平分线的性质;勾股定理;等腰直角三角形.
【专题】等腰三角形与直角三角形;运算能力.
【答案】C
【分析】根据平移的性质,得出△BB′C′为等腰三角形及△AB′E为等腰直角三角形,求出AE的长,据此可解决问题.
【解答】解:由平移可知,
BC∥B′C′,B′C′=BC=6,
∴∠CBC′=∠BC′B′.
又∵BC′平分∠CBB′,
∴∠CBC′=∠B′BC′,
∴∠B′BC′=∠BC′B′,
∴BB′=B′C′=6.
∵AB,
∴AB′,
∴AE,
∴CE=AC﹣AE=6﹣().
故选:C.
【点评】本题主要考查了平移的性质、角平分线的性质、勾股定理及等腰直角三角形,熟知平移的性质及等腰直角三角形的性质是解题的关键.
5.(2025 白山模拟)“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥,如图,将边长为1cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A.1cm B.2cm C. D.
【考点】利用平移设计图案;全等图形.
【专题】推理能力.
【答案】C
【分析】根据正方形的性质、勾股定理求出BD,根据平移的概念求出BB′,计算即可.
【解答】解:∵四边形ABCD是边长为1cm的正方形,
∴BD(cm),
由平移的性质可知BB′=1cm,
∴.
故选:C.
【点评】本题考查的是平移的性质、正方形的性质,勾股定理,根据平移的概念求出BB′是解题的关键.
6.(2025 碧江区 一模)在平面直角坐标系中,线段AB的端点分别为A(1,3)、B(2,2),将线段AB平移到A1B1,且点A1的坐标为(5,4),则点B1的坐标为( )
A.(6,3) B.(3,6) C.(4,5) D.(5,4)
【考点】坐标与图形变化﹣平移.
【专题】平面直角坐标系;符号意识.
【答案】A
【分析】根据点A的坐标平移后所得点的坐标得到平移规律,再根据平移规律可得点B的坐标.
【解答】解:B(2,2)向右平移4个单位,向上平移一个单位得到B1(6,3),
故选:A.
【点评】本题考查了坐标与图形变化﹣平移,确定平移规律是解题的关键.
7.(2025 南明区二模)南南在画板上画出两条不平行的直线a,b(如图①),他发现,如果利用平移变换就可以知道这两条直线所成的角的度数,将直线b向左平移与直线a交于一点(如图②),则直线a,b所成的锐角的度数为( )
A.45° B.30° C.25° D.40°
【考点】平移的性质.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】根据平移的性质即可解决问题.
【解答】解:由题知,
∵直线c由直线b平移得到,
∴c∥b.
又∵直线a与直线c所成锐角的度数为30°,
∴直线a,b所成锐角的度数为30°.
故选:B.
【点评】本题主要考查了平移的性质,熟知平移的性质是解题的关键.
8.(2025 琼中县三模)如图,已知点A(1,2),B(2,﹣1),平移线段AB,使点B落在点B1(﹣1,﹣2)处,则点A的对应点A1的坐标为( )
A.(﹣2,2) B.(﹣2,1) C.(﹣2,0) D.(﹣1,1)
【考点】坐标与图形变化﹣平移.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】由点B的坐标得出平移的方式,再根据平移的方式得出A点平移后的点的坐标即可.
【解答】解:∵点A(1,2),B(2,﹣1),平移线段AB,点B落在点B1(﹣1,﹣2)处,
∴AB先向下移动1个单位,再向左移动3个单位,
∵A(1,2),
∴A′(1﹣3,2﹣1),即A′(﹣2,1),
故选:B.
【点评】本题主要考查了坐标与图形变化﹣平移,熟知横坐标,右移加,左移减;纵坐标,上移加,下移减是解题的关键.
9.(2025 辽阳模拟)如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为( )
A.7cm2 B.6cm2 C.5cm2 D.4cm2
【考点】平移的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;推理能力.
【答案】B
【分析】由平移的性质可得A'E=2cm,AE=1cm,可求B'E=2cm,DE=3cm,即可求解.
【解答】解:如图,设AD与A'B'交于点E,
∵将边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,
∴A'E=2cm,AE=1cm,
∴B'E=2cm,DE=3cm,
∴阴影部分的面积=2×3=6cm2,
故选:B.
【点评】本题考查了正方形的性质,平移的性质,掌握平移的性质是解题的关键.
10.(2025 琼山区校级二模)如图,在平面直角坐标系中,点A,B分别在x轴的正半轴和y轴的正半轴上,OA=2,OB=1.将线段AB平移至线段A′B′,若点A′的坐标为(4,﹣3),则点B′的坐标为( )
A.(2,2) B.(2,﹣2) C.(2,﹣4) D.(3,﹣3)
【考点】坐标与图形变化﹣平移.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】根据题意,求出点A和点B的坐标,再结合点A和其对应点A′的坐标得出平移的方向和距离即可解决问题.
【解答】解:由题知,
因为OA=2,OB=1,
所以点A坐标为(2,0),点B坐标为(0,1).
又因为平移后点A的对应点A′的坐标为(4,﹣3),
则4﹣2=2,﹣3﹣0=﹣3,
所以0+2=2,1﹣3=﹣2,
所以点B′的坐标为(2,﹣2).
故选:B.
【点评】本题主要考查了坐标与图形变化﹣平移,熟知平移时点的坐标变化规律是解题的关键.
二.填空题(共5小题)
11.(2025 樟树市校级三模)如图,在△ABC中,∠ABC=90°,BC=9,把△ABC沿射线AB平移至△EFG处,EG与BC交于点M,若CM=3,FB=4,则图中阴影部分的面积为 30 .
【考点】平移的性质.
【专题】平移、旋转与对称;推理能力.
【答案】30.
【分析】利用平移的性质得到FG=BC=9,△ABC≌△EFG,则S△ABC=S△EFG,所以S四边形AEMC=S梯形BFGM,然后根据梯形的面积公式计算.
【解答】解:∵△AB沿射线AB方向平移至△EFG,
∴FG=BC=9,△ABC≌△EFG,
∴S△ABC=S△EFG,BM=BC﹣CM=9﹣3=6,
即S四边形AEMC+S△EBM=S△EBM+S梯形BFGM,
∴S四边形AEMC=S梯形BFGM(6+9)×4=30.
故答案为:30.
【点评】本题考查了平移的性质:把求图中阴影部分的面积转化求为梯形BFGM的面积是解决问题的关键.
12.(2025 旬邑县校级模拟)如图,在△ABC中,AB⊥BC,AB=6,AC=10.将△ABC沿AC方向平移一段距离后得到△DEF,DE交BC于点G.连接BE,则阴影部分的周长为 24 .
【考点】平移的性质.
【专题】平移、旋转与对称;推理能力.
【答案】24.
【分析】根据勾股定理求出BC=8,根据平移的性质求出BE=AD,AB=DE,再根据周长定义求解即可.
【解答】解:∵AB⊥BC,AB=6,AC=10,
∴,
由平移的性质可得,BE=AD,AB=DE,
∴阴影部分的周长为BE+BC+DE+CD=AD+BC+AB+CD,
∵AC=AD+CD,
∴阴影部分的周长为BC+AB+AC=8+6+10=24,
故答案为:24.
【点评】此题考查了平移的性质,熟记平移的性质是解题的关键.
13.(2025 武侯区校级模拟)如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A'B'C',连接A'C,则线段A'C的长为 4 .
【考点】平移的性质.
【专题】等腰三角形与直角三角形;几何直观.
【答案】4.
【分析】根据平移性质,判定△A′B′C为等边三角形,然后求解.
【解答】解:由题意,得BB′=2,
∴B′C=BC﹣BB′=4.
由平移性质,可知A′B′=AB=4,∠A′B′C=∠ABC=60°,
∴A′B′=B′C,且∠A′B′C=60°,
∴△A′B′C为等边三角形,
∴A'C=A'B'=4,
故答案为:4.
【点评】本题考查的是平移的性质,熟知图形平移后新图形与原图形的形状和大小完全相同是解答此题的关键.
14.(2025 绥中县一模)在平面直角坐标系中,将点P(3,5)向上平移2个单位长度后得到点P′的坐标为 (3,7) .
【考点】坐标与图形变化﹣平移.
【专题】平面直角坐标系;平移、旋转与对称;几何直观.
【答案】(3,7).
【分析】根据点的坐标平移规则:左减右加,上加下减求解即可.
【解答】解:根据点的坐标平移规则:左减右加,上加下减可得点P′的坐标为(3,5+2),即(3,7),
故答案为:(3,7).
【点评】本题考查坐标与图形变换﹣平移变换,熟练掌握该知识点是关键.
15.(2025 新宾县校级模拟)如图所示的是某商场门前的台阶,现该商场经理要在台阶上铺上一块矩形红地毯,则这块红地毯的长至少为 18m .
【考点】生活中的平移现象.
【专题】平移、旋转与对称;几何直观.
【答案】18m.
【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积即可.
【解答】解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为10米,8米,
故地毯的长度为8+10=18(米).
故答案为:18m.
【点评】此题考查了生活中的平移现象,掌握平移现象的特点是关键.
三.解答题(共5小题)
16.(2025 西安模拟)如图,在平面直角坐标系xOy中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2).现将△ABC平移,使点A与点A′重合,点B、C的对应点分别是点B′、C′.
(1)请画出平移后的△A′B′C′,并写出点B′的坐标 B′(﹣4,1) ;
(2)点P是△ABC内的一点,当△ABC平移到△A′B′C′后,若点P的对应点P′的坐标为(a,b),则点P的坐标为 (a+5,b+2) .
【考点】作图﹣平移变换.
【专题】作图题;几何直观.
【答案】(1)B′(﹣4,1),图见解析;
(2)点P的坐标为(a+5,b+2).
【分析】(1)先根据题意求出平移方向,从而求出B′,C′的坐标,画出图形即可;
(2)根据(1)中的平移方向,即可求解.
【解答】解:(1)∵点A′的坐标是(﹣2,2),点A的坐标是(3,4),
∴平移方向是先向右平移5个单位长度,再向下平移2个单位长度,
∵点B的坐标是(1,3),点C的坐标是(4,1),
∴点B′的坐标是(﹣4,1),点C′的坐标是(﹣1,﹣1),
∴平移后的△A′B′C′如图所示:
(2)由(1)得:平移方向是先向右平移5个单位长度,再向下平移2个单位长度,
∵点P的对应点P′的坐标为(a,b),
∴点P的坐标为(a+5,b+2);
【点评】本题主要考查了作图﹣平移变换,正确得出对应点位置是解题关键.
17.(2025 岳麓区校级三模)如图,已知△ABC的顶点A(﹣1,4),B(﹣4,﹣1),C(1,1).将△ABC向右平移4个单位长度,再向下平移3个单位长度得到△A'B'C',其中点A',B',C'分别为点A,B,C的对应点.
(1)画出△A'B'C',并直接写出点A'的坐标;
(2)求△ABC的面积.
【考点】作图﹣平移变换.
【专题】平移、旋转与对称;几何直观;运算能力.
【答案】(1)画图见解答;点A'的坐标为(3,1).
(2).
【分析】(1)根据平移的性质作图,即可得出答案.
(2)利用割补法求三角形的面积即可.
【解答】解:(1)如图,△A'B'C'即为所求.
由图可得,点A'的坐标为(3,1).
(2)△ABC的面积为.
【点评】本题考查作图﹣平移变换,熟练掌握平移的性质是解答本题的关键.
18.(2025 滁州三模)如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).
(1)将△ABC向下平移2个单位长度,再向左平移3个单位长度,得到△A1B1C1,请画出△A1B1C1.
(2)在AC上作一点D,使得点D到AB和BC的距离相等.(不要求写作法,保留作图痕迹)
【考点】作图﹣平移变换;角平分线的性质;等腰三角形的性质.
【专题】平移、旋转与对称;几何直观.
【答案】(1)见解答.
(2)见解答.
【分析】(1)根据平移的性质作图即可.
(2)结合等腰三角形的性质和角平分线的性质,在BC的延长线上取点E,使BE=AB,取AE的中点F,作射线BF交AC于点D,则点D即为所求.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,在BC的延长线上取点E,使BE=AB,取AE的中点F,作射线BF交AC于点D,
此时BD为∠ABC的平分线,
∴点D到AB和BC的距离相等,
则点D即为所求.
【点评】本题考查作图﹣平移变换、角平分线的性质、等腰三角形的性质,熟练掌握轴对称的性质、角平分线的性质、等腰三角形的性质是解答本题的关键.
19.(2025 香坊区三模)如图是由边长为1个单位长度的小正方形组成的网格,每个小正方形的顶点叫做格点.线段AB的端点均在格点上.
(1)将线段AB向左移动一个单位长度,再向上移动一个单位长度,得到线段CD,点A的对应点为C,点B的对应点为D,画出四边形ACDB,并直接写出四边形ACDB的周长;
(2)在(1)的条件下,在线段AB上画点E,并连接EC、ED,使EC=ED.(仅用无刻度的直尺作图,并保留作图痕迹.)
【考点】作图﹣平移变换;勾股定理.
【专题】平移、旋转与对称;空间观念;几何直观.
【答案】(1)画图见解答;.
(2)见解答.
【分析】(1)根据平移的性质作图即可;结合勾股定理计算即可.
(2)作线段CD的垂直平分线,交AB于点E,则点E即为所求.
【解答】解:(1)如图,四边形ACDB即为所求.
由勾股定理得AC=BD,AB=CD,
∴四边形ACDB的周长为AC+BD+AB+CD.
(2)如图,作线段CD的垂直平分线,交AB于点E,连接EC、ED,
则点E即为所求.
【点评】本题考查作图﹣平移变换、勾股定理,熟练掌握平移的性质、勾股定理是解答本题的关键.
20.(2025 武汉模拟)如图是由小正方形组成的7×4网格,每个小正方形的顶点叫做格点.平行四边形ABCD四个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.
(1)在图(1)中,点E是边AD上一点,在线段ED上画一点F,使得DF=AE;
(2)在(1)的基础上,将BE平移到CG,画出线段CG.
(3)在图(2)中,平行四边形对角线的交点为O,在AD上画一点H,使得HB=HD,连接BH;
(4)在(3)的基础上,将BH绕着O点顺时针旋转∠AHB的度数得到线段MN,点M与点B对应,点N与点H对应,画出线段MN.
【考点】作图﹣平移变换;旋转的性质;线段垂直平分线的性质;勾股定理;勾股定理的逆定理;平行四边形的性质.
【专题】作图题;几何直观.
【答案】见解析.
【分析】(1)延长BE交网格线于点J,取格点K,连接JK交AD于点F,点F即为所求;
(2)线段JK交网格线于点I,连接CI,延长CI交AD于点G,线段CG即为所求;
(3)取格点J,连接OJ交AD于点H,连接BH,点H即为所求;
(4)取格点M,P,连接OP交AD于点N,线段MN即为所求.
【解答】解:(1)如图1中,点F即为所求;
(2)如图1中,线段CG即为所求;
(3)如图2中,点H即为所求;
(4)如图2中,线段MN即为所求.
【点评】本题考查作图﹣平移后,线段的垂直平分线的性质,勾股定理,勾股定理的逆定理,平行四边形的性质,性质的性质,解题的关键是掌握相关知识解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
