2026年中考数学一轮复习 图形的旋转(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 图形的旋转(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2026年中考数学一轮复习 图形的旋转
一.选择题(共10小题)
1.(2025 永寿县校级模拟)下列图形中,不是轴对称图形,但是中心对称图形的是( )
A. B.
C. D.
2.(2025 大同模拟)科技馆是青少年科普实践的重要基地,通过互动性强的展览和活动,激发青少年的好奇心和探索精神.以下科技馆的标识中,文字上方的图案是中心对称图形的是( )
A.山西省科技馆 B.甘肃省科技馆
C.合肥市科技馆 D.滨州市科技馆
3.(2025 兴庆区校级一模)大约在两千四百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验,并在《墨经》中做了记载,如图,在实验中,物和像属于以下哪种变换( )
A.平移变换 B.对称变换 C.旋转变换 D.位似变换
4.(2025 大庆模拟)如图,△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交DE于点F,下列结论中不一定正确的是( )
A.∠ACD=∠EFB B.AC∥DE C.AB=DE D.BF⊥CE
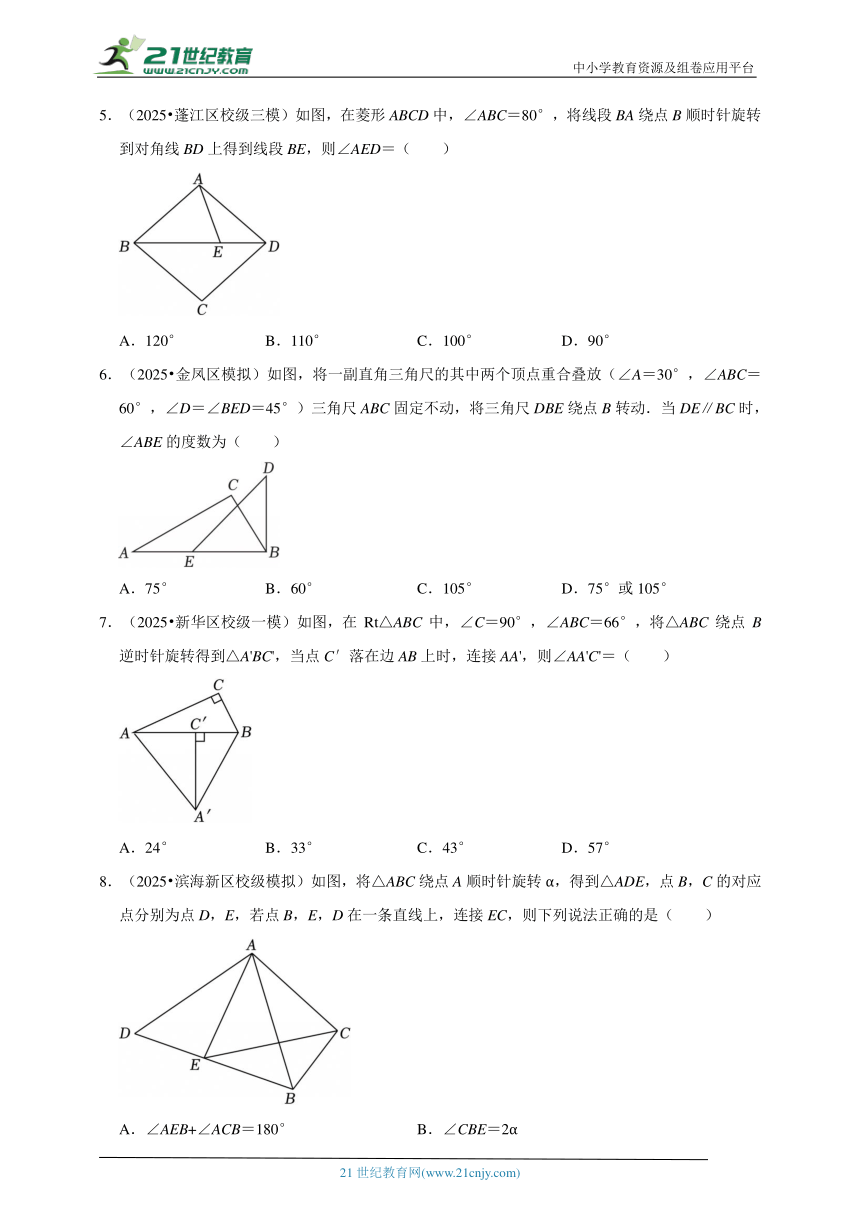
5.(2025 蓬江区校级三模)如图,在菱形ABCD中,∠ABC=80°,将线段BA绕点B顺时针旋转到对角线BD上得到线段BE,则∠AED=( )
A.120° B.110° C.100° D.90°
6.(2025 金凤区模拟)如图,将一副直角三角尺的其中两个顶点重合叠放(∠A=30°,∠ABC=60°,∠D=∠BED=45°)三角尺ABC固定不动,将三角尺DBE绕点B转动.当DE∥BC时,∠ABE的度数为( )
A.75° B.60° C.105° D.75°或105°
7.(2025 新华区校级一模)如图,在Rt△ABC中,∠C=90°,∠ABC=66°,将△ABC绕点B逆时针旋转得到△A'BC',当点C′落在边AB上时,连接AA',则∠AA'C'=( )
A.24° B.33° C.43° D.57°
8.(2025 滨海新区校级模拟)如图,将△ABC绕点A顺时针旋转α,得到△ADE,点B,C的对应点分别为点D,E,若点B,E,D在一条直线上,连接EC,则下列说法正确的是( )
A.∠AEB+∠ACB=180° B.∠CBE=2α
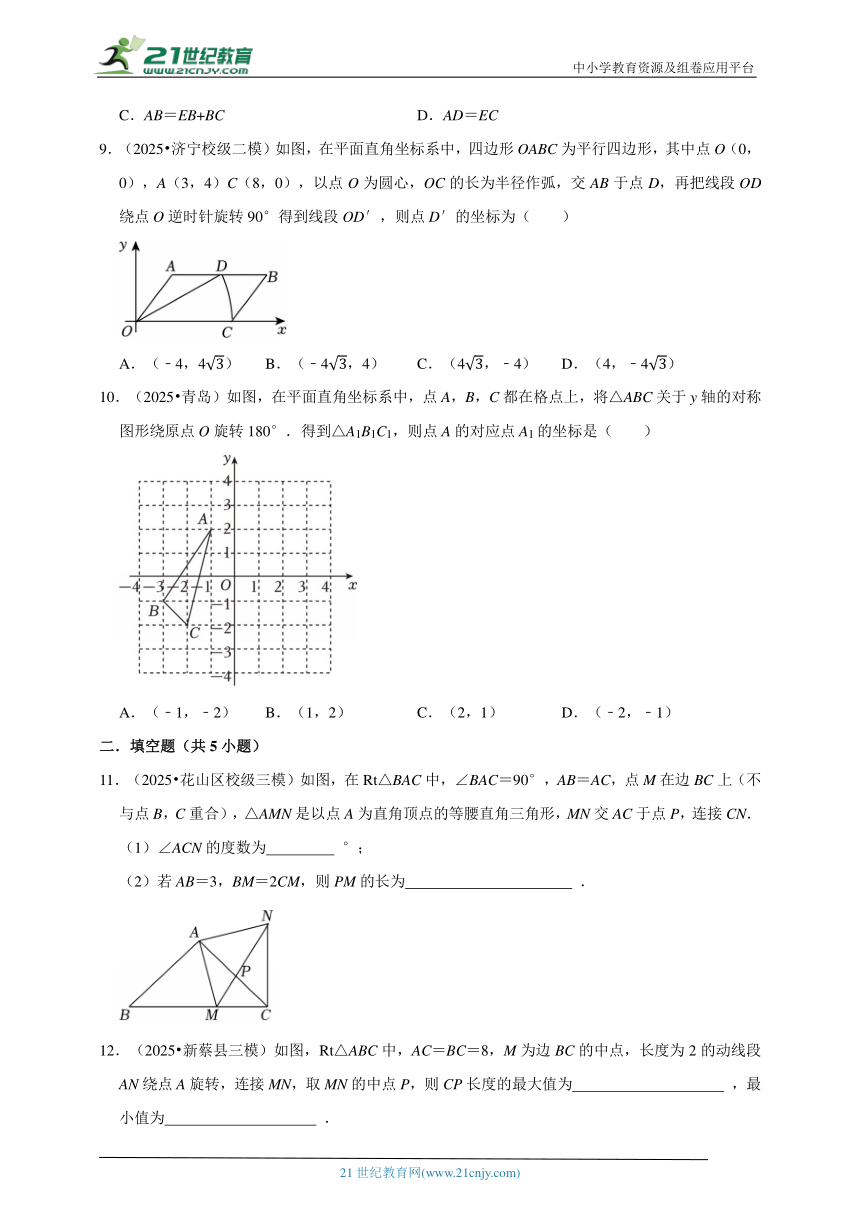
C.AB=EB+BC D.AD=EC
9.(2025 济宁校级二模)如图,在平面直角坐标系中,四边形OABC为平行四边形,其中点O(0,0),A(3,4)C(8,0),以点O为圆心,OC的长为半径作弧,交AB于点D,再把线段OD绕点O逆时针旋转90°得到线段OD′,则点D′的坐标为( )
A.(﹣4,4) B.(﹣4,4) C.(4,﹣4) D.(4,﹣4)
10.(2025 青岛)如图,在平面直角坐标系中,点A,B,C都在格点上,将△ABC关于y轴的对称图形绕原点O旋转180°.得到△A1B1C1,则点A的对应点A1的坐标是( )
A.(﹣1,﹣2) B.(1,2) C.(2,1) D.(﹣2,﹣1)
二.填空题(共5小题)
11.(2025 花山区校级三模)如图,在Rt△BAC中,∠BAC=90°,AB=AC,点M在边BC上(不与点B,C重合),△AMN是以点A为直角顶点的等腰直角三角形,MN交AC于点P,连接CN.
(1)∠ACN的度数为 °;
(2)若AB=3,BM=2CM,则PM的长为 .
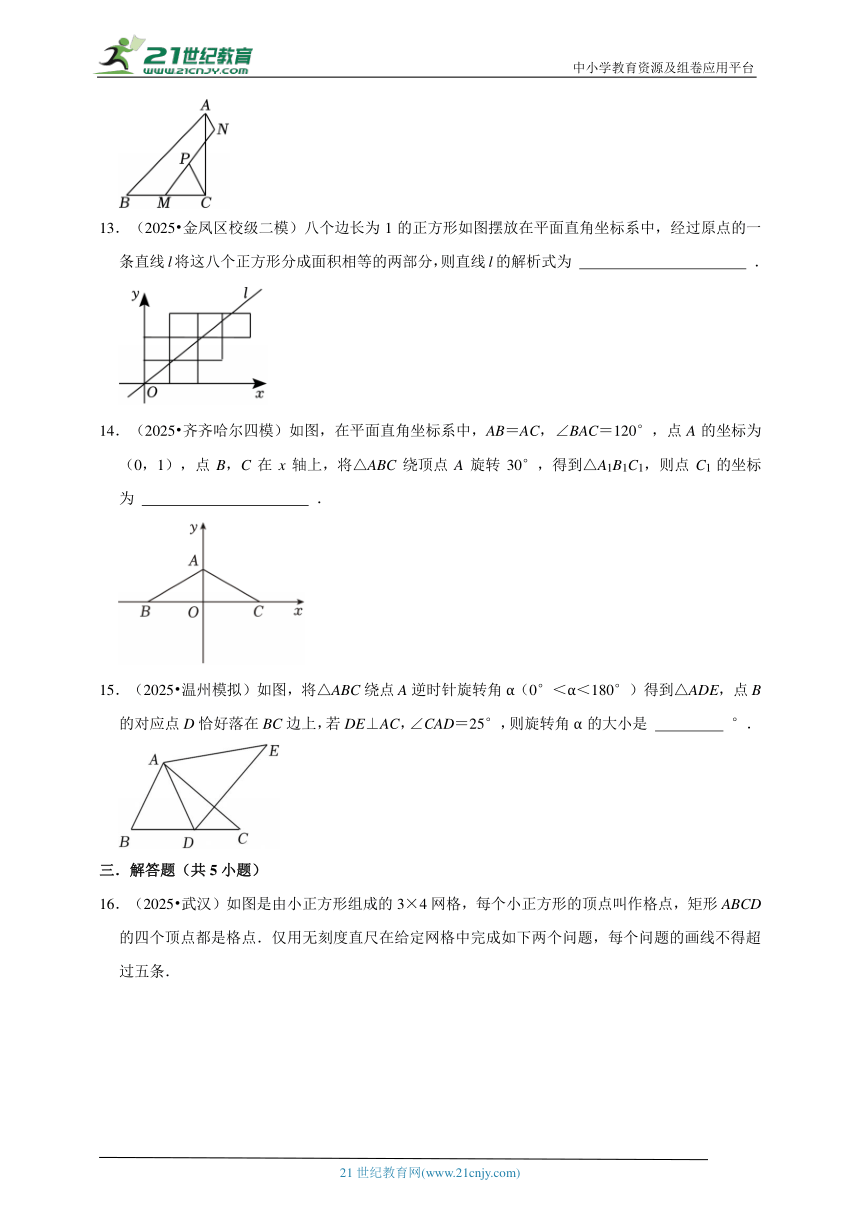
12.(2025 新蔡县三模)如图,Rt△ABC中,AC=BC=8,M为边BC的中点,长度为2的动线段AN绕点A旋转,连接MN,取MN的中点P,则CP长度的最大值为 ,最小值为 .
13.(2025 金凤区校级二模)八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则直线l的解析式为 .
14.(2025 齐齐哈尔四模)如图,在平面直角坐标系中,AB=AC,∠BAC=120°,点A的坐标为(0,1),点B,C在x轴上,将△ABC绕顶点A旋转30°,得到△A1B1C1,则点C1的坐标为 .
15.(2025 温州模拟)如图,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE,点B的对应点D恰好落在BC边上,若DE⊥AC,∠CAD=25°,则旋转角α的大小是 °.
三.解答题(共5小题)
16.(2025 武汉)如图是由小正方形组成的3×4网格,每个小正方形的顶点叫作格点,矩形ABCD的四个顶点都是格点.仅用无刻度直尺在给定网格中完成如下两个问题,每个问题的画线不得超过五条.
(1)如图1,E是格点,先将点E绕点A逆时针旋转90°,画对应点F,再画直线FG交AB于点G,使直线FG平分矩形ABCD的面积.
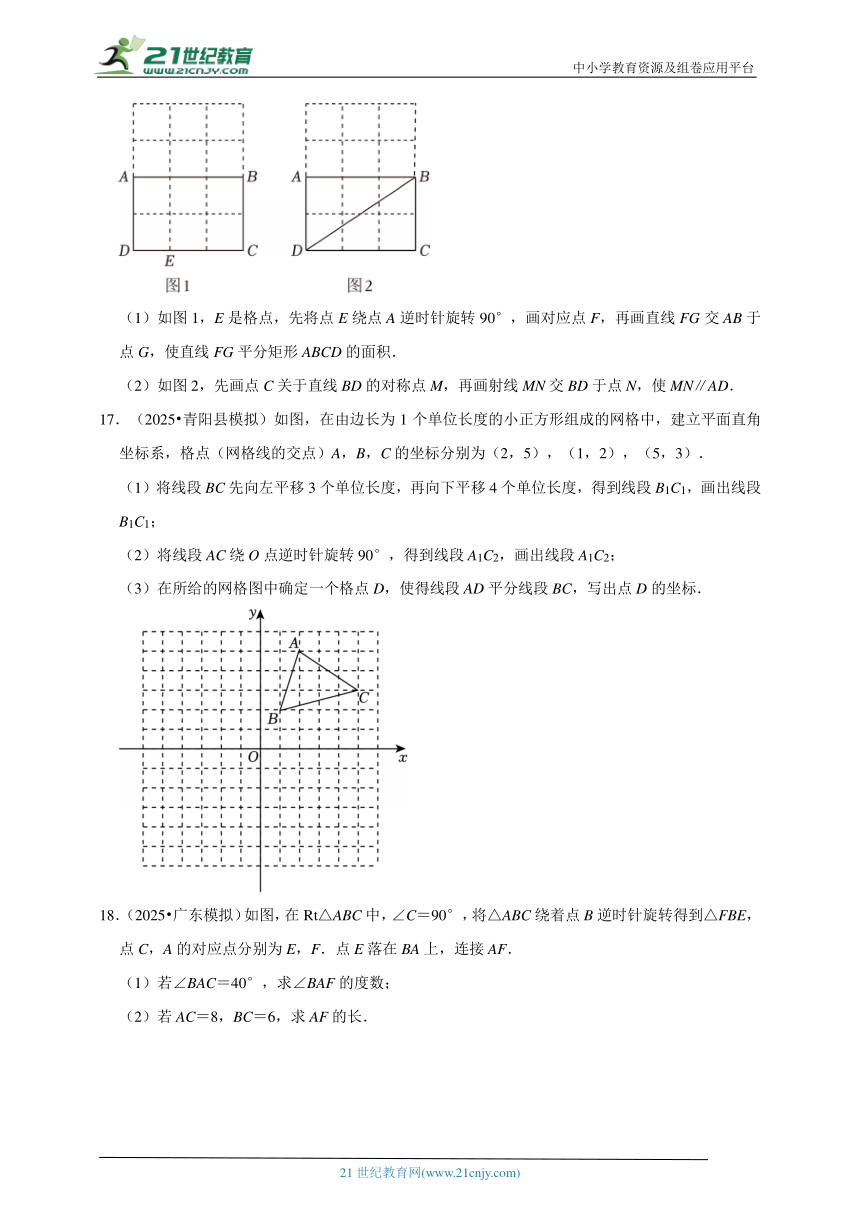
(2)如图2,先画点C关于直线BD的对称点M,再画射线MN交BD于点N,使MN∥AD.
17.(2025 青阳县模拟)如图,在由边长为1个单位长度的小正方形组成的网格中,建立平面直角坐标系,格点(网格线的交点)A,B,C的坐标分别为(2,5),(1,2),(5,3).
(1)将线段BC先向左平移3个单位长度,再向下平移4个单位长度,得到线段B1C1,画出线段B1C1;
(2)将线段AC绕O点逆时针旋转90°,得到线段A1C2,画出线段A1C2;
(3)在所给的网格图中确定一个格点D,使得线段AD平分线段BC,写出点D的坐标.
18.(2025 广东模拟)如图,在Rt△ABC中,∠C=90°,将△ABC绕着点B逆时针旋转得到△FBE,点C,A的对应点分别为E,F.点E落在BA上,连接AF.
(1)若∠BAC=40°,求∠BAF的度数;
(2)若AC=8,BC=6,求AF的长.
19.(2025 朝阳区校级模拟)如图,在矩形ABCD中,AB=5,BC=8,AE=3,点P沿AB﹣BC运动,将点P绕点E逆时针旋转90°得到点Q.
(1)EP平分矩形面积时,求BP的长;
(2)E、Q、C三点共线时,求AP的长;
(3)CQ的最小值为 ,点Q的路径长为 ;
(4)当点Q在四边形内形时,四边形PBCQ面积的最大值为 ,此时线段AP的长为 .
20.(2025 河南模拟)综合与实践:
定义:将三角形沿过顶点的直线折叠,折叠后的另一个顶点恰好落在这个三角形的边上(不含顶点)时,此时折痕被称为“落边折痕”.
特例感知:已知△ABC,D为AC边上一点,将△ABC沿BD折叠,使得点A恰好落在BC边上(不含点C),此时折痕BD称为“落边折痕”.
探究1:如图①,若△ABC是直角三角形,其中∠A=90°,∠ABC=60°,AB=1,若点D为AC边上一点,将△ABC沿着BD折叠后,点A恰好落在BC边上的点E处,求“落边折痕”BD的长;
探究2:如图②,若△ABC是等腰三角形,其中∠A=120°,请求出“落边折痕BD”将其分割后的△ABD与△BCD的面积比;
探究3:如图③,若△ABC是等腰三角形,其中AB=AC=5,BC=6,请求出其“落边折痕”的长度.
2026年中考数学一轮复习 图形的旋转
参考答案与试题解析
一.选择题(共10小题)
1.(2025 永寿县校级模拟)下列图形中,不是轴对称图形,但是中心对称图形的是( )
A. B.
C. D.
【考点】中心对称图形;轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.
【解答】解:A.该三角形既不是轴对称图形,也不是中心对称图形,故本选项不符合题意;
B.正方形是轴对称图形,也是中心对称图形,故本选项不符合题意;
C.正五边形是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.平行四边形不是轴对称图形,是中心对称图形,故本选项符合题意;
故选:D.
【点评】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
2.(2025 大同模拟)科技馆是青少年科普实践的重要基地,通过互动性强的展览和活动,激发青少年的好奇心和探索精神.以下科技馆的标识中,文字上方的图案是中心对称图形的是( )
A.山西省科技馆 B.甘肃省科技馆
C.合肥市科技馆 D.滨州市科技馆
【考点】中心对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】C
【分析】中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形可得答案.
【解答】解:A、选项图形不是中心对称图形,不符合题意;
B、选项图形不是中心对称图形,不符合题意;
C、选项图形是中心对称图形,符合题意;
D、选项图形不是中心对称图形,不符合题意.
故选:C.
【点评】本题主要考查了中心对称图形,掌握中心对称图形的定义是关键.
3.(2025 兴庆区校级一模)大约在两千四百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验,并在《墨经》中做了记载,如图,在实验中,物和像属于以下哪种变换( )
A.平移变换 B.对称变换 C.旋转变换 D.位似变换
【考点】几何变换的类型.
【专题】图形的相似;几何直观.
【答案】D
【分析】根据位似变换的定义判断即可.
【解答】解:小孔成倒像的实验,物和像属于位似变换.
故选:D.
【点评】本题考查几何变换的类型,平移变换,轴对称变换,旋转变换,位似变换等知识,解题的关键是理解各种变换的定义.
4.(2025 大庆模拟)如图,△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交DE于点F,下列结论中不一定正确的是( )
A.∠ACD=∠EFB B.AC∥DE C.AB=DE D.BF⊥CE
【考点】旋转的性质;平行线的判定.
【专题】平移、旋转与对称;几何直观.
【答案】B
【分析】设BF与CE相交于点G,由旋转得可得∠E=∠B=30°,AB=DE,∠BCE=∠ACD=60°,根据∠EGF=∠BGC,可得∠EFB=∠BCG=60°,则∠ACD=∠EFB.根据∠B=30°,∠BCG=60°,可得∠BGC=90°,即BF⊥CE.
【解答】解:设BF与CE相交于点G,
∵△ABC绕点C顺时针旋转60°得到△DEC,
∴∠E=∠B=30°,AB=DE,∠BCE=∠ACD=60°,
∵∠EGF=∠BGC,
∴∠EFB=∠BCG=60°,
∴∠ACD=∠EFB.
故A,C选项正确,不符合题意;
∵∠B=30°,∠BCG=60°,
∴∠BGC=90°,
∴BF⊥CE.
故D选项正确,不符合题意;
根据题意知条件不能得出AC∥DE,
故B选项不正确,符合题意.
故选:B.
【点评】本题考查旋转的性质、平行线的判定,熟练掌握旋转的性质是解答本题的关键.
5.(2025 蓬江区校级三模)如图,在菱形ABCD中,∠ABC=80°,将线段BA绕点B顺时针旋转到对角线BD上得到线段BE,则∠AED=( )
A.120° B.110° C.100° D.90°
【考点】旋转的性质;菱形的性质.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】先由菱形的性质得∠ABE=∠CBE∠ABC=40°,再由等腰三角形的性质和三角形内角和定理即可得出答案.
【解答】解:∵四边形ABCD是菱形,∠ABC=80°,
∴∠ABE=∠CBE∠ABC=40°,
∵BA=BE,
∴∠BAE=∠BEA(180°﹣40°)=70°,
∴∠AED=180°﹣∠AEB=110°,
故选:B.
【点评】本题考查了菱形的性质、等腰三角形的性质以及三角形内角和定理,熟练掌握菱形的性质和等腰三角形的性质是解题的关键.
6.(2025 金凤区模拟)如图,将一副直角三角尺的其中两个顶点重合叠放(∠A=30°,∠ABC=60°,∠D=∠BED=45°)三角尺ABC固定不动,将三角尺DBE绕点B转动.当DE∥BC时,∠ABE的度数为( )
A.75° B.60° C.105° D.75°或105°
【考点】旋转的性质;平行线的性质.
【专题】平移、旋转与对称;几何直观;推理能力.
【答案】D
【分析】分两种情况,运用平行线的性质求解即可.
【解答】解:如图①,
∵DE∥BC,
∴∠CBD=∠D=45°,
∴∠ABD=∠ABC﹣∠CBD=60°﹣45°=15°,
∵∠DBE=90°,
∴∠ABE=∠DBE﹣∠ABD=90°﹣15°=75°,
如图②,当DE∥BC时,
∵DE∥BC,
∴∠CBE=∠E=45°,
∴∠ABE=∠ABC+∠CBE=60°+45°=105°.
综上所述,∠ABE的度数为75°或105°,
故选:D.
【点评】本题主要考查了旋转的性质发,平行线的性质,解答本题的关键是熟练掌握旋转的性质.
7.(2025 新华区校级一模)如图,在Rt△ABC中,∠C=90°,∠ABC=66°,将△ABC绕点B逆时针旋转得到△A'BC',当点C′落在边AB上时,连接AA',则∠AA'C'=( )
A.24° B.33° C.43° D.57°
【考点】旋转的性质.
【专题】等腰三角形与直角三角形;平移、旋转与对称;推理能力.
【答案】B
【分析】由旋转的性质可得AB=A'B,∠ABC=66°=∠A'BC',∠C=90°=∠A'C'B,由等腰三角形的性质可得∠BAA'=57°,即可求解.
【解答】解:∵将△ABC绕点B逆时针旋转得到△A'BC',
∴AB=A'B,∠ABC=66°=∠A'BC',∠C=90°=∠A'C'B,
∴∠BAA'=57°,
∴∠AA'C'=33°,
故选:B.
【点评】本题考查了旋转的性质,等腰三角形的性质,掌握旋转的性质是解题的关键.
8.(2025 滨海新区校级模拟)如图,将△ABC绕点A顺时针旋转α,得到△ADE,点B,C的对应点分别为点D,E,若点B,E,D在一条直线上,连接EC,则下列说法正确的是( )
A.∠AEB+∠ACB=180° B.∠CBE=2α
C.AB=EB+BC D.AD=EC
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】由旋转的性质得到△ADE≌△ABC,推出∠AED=∠ACB,由邻补角的性质得到∠AEB+∠AED=180°,推出∠AEB+∠ACB=180°,由全等三角形的性质推出∠ABC=∠D,AD=AB,由等腰三角形的性质得到∠ABD=∠D,而∠BAD=α,求出∠D+∠ABD=(180°﹣α),得到EBC=180°﹣α,由全等三角形的性质得到DE=BC,因此EB+BC=DB,判定AB不一定等于EB+BC,由△ADE≌△ABC,推出AD=AB,得到AD和CE不一定相等.
【解答】解:由旋转的性质得到:△ADE≌△ABC,
∴∠AED=∠ACB,
∵∠AEB+∠AED=180°,
∴∠AEB+∠ACB=180°,
故A符合题意;
∵△ADE≌△ABC,
∴∠ABC=∠D,AD=AB,
∴∠ABD=∠D,
由旋转的性质得到:∠BAD=α,
∴∠D+∠ABD=(180°﹣α),
∴EBC=∠ABD+∠ABC=∠ABD+∠D=180°﹣α,
故B不符合题意;
∵△ADE≌△ABC,
∴DE=BC,
∴EB+BC=BE+DE=DB,
∵DE不一定等于AB,
∴AB不一定等于EB+BC,
故C不符合题意;
∵△ADE≌△ABC,
∴AD=AB,
∵AB和CE不一定相等,
∴AD和CE不一定相等,
故D不符合题意.
故选:A.
【点评】本题考查旋转的性质,关键是由旋转的性质得到△ADE≌△ABC,∠BAD=α.
9.(2025 济宁校级二模)如图,在平面直角坐标系中,四边形OABC为平行四边形,其中点O(0,0),A(3,4)C(8,0),以点O为圆心,OC的长为半径作弧,交AB于点D,再把线段OD绕点O逆时针旋转90°得到线段OD′,则点D′的坐标为( )
A.(﹣4,4) B.(﹣4,4) C.(4,﹣4) D.(4,﹣4)
【考点】坐标与图形变化﹣旋转;全等三角形的判定与性质;平行四边形的性质;旋转的性质.
【专题】平面直角坐标系;图形的全等;多边形与平行四边形;运算能力.
【答案】A
【分析】如图,延长BA交y轴于点E,过点D′作D′F⊥x轴于点F.证明△ODE≌△OD′F(AAS),推出D′F=DE=4,OF=OE=4可得结论.
【解答】解:如图,延长BA交y轴于点E,过点D′作D′F⊥x轴于点F.
由题意,可知DE⊥y轴,AE=3,OE=4.由旋转的性质,可知OD=OC=8,
∴DE4,
∵OD=OD′,∠DOD′=90°,
∴∠EOD+∠EOD′=90°,
∵∠D′OF+∠EOD′=90°.
∴∠D′OE=∠DOE,
∵∠DEO=∠D′FO=90°,
∴△ODE≌△OD′F(AAS),
∴D′F=DE=4,OF=OE=4.
∴点D′的坐标为(﹣4,4),
故选:A.
【点评】本题考查坐标与图形性质,全等三角形的判定和性质,平行四边形的性质,旋转的性质,解题的关键是学会添加常用辅助线,正确寻找全等三角形解决问题.
10.(2025 青岛)如图,在平面直角坐标系中,点A,B,C都在格点上,将△ABC关于y轴的对称图形绕原点O旋转180°.得到△A1B1C1,则点A的对应点A1的坐标是( )
A.(﹣1,﹣2) B.(1,2) C.(2,1) D.(﹣2,﹣1)
【考点】坐标与图形变化﹣旋转;关于x轴、y轴对称的点的坐标.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】先根据图中△ABC的位置求出点A的坐标,再根据关于y轴的对称可求解点A2,再根据绕原点O旋转180°即可求解点A1的坐标.
【解答】解:在平面直角坐标系中,点A(﹣1,2),
∴点A关于y轴对称的点A2(1,2),
将点A2(1,2)绕原点O旋转180°,
∴如图,点A1(﹣1,﹣2).
故选:A.
【点评】本题考查了平面直角坐标系中点的变换,熟练掌握点的对称与旋转是解决本题的关键.
二.填空题(共5小题)
11.(2025 花山区校级三模)如图,在Rt△BAC中,∠BAC=90°,AB=AC,点M在边BC上(不与点B,C重合),△AMN是以点A为直角顶点的等腰直角三角形,MN交AC于点P,连接CN.
(1)∠ACN的度数为 45 °;
(2)若AB=3,BM=2CM,则PM的长为 .
【考点】旋转的性质;全等三角形的判定与性质;勾股定理;等腰直角三角形.
【专题】图形的全等;等腰三角形与直角三角形;运算能力;推理能力.
【答案】(1)45;
(2).
【分析】(1)由旋转得AM=AN,∠MAN=90°,因为AB=AC,∠BAC=90°,所以∠B=∠ACB=45°,∠BAM=∠CAN=90°﹣∠CAM,可根据“SAS”证明△ABM≌△ACN,得∠B=∠ACN=45°,于是得到问题的答案;
(2)作PF⊥CB于点F,PE⊥CN于点E,由AB=AC=3,求得BC=3,由BM=2CM,求得CM,BM=CN=2,因为∠MCN=90°,所以MN,由角平分线的性质得PF=PE,则S△CPMCM PE,S△CPNCN PE,所以,则PMMN,于是得到问题的答案.
【解答】解:(1)∵△AMN是以点A为直角顶点的等腰直角三角形,
∴AM=AN,∠MAN=90°,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,∠BAM=∠CAN=90°﹣∠CAM,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(SAS),
∴∠B=∠ACN=45°,
故答案为:45.
(2)作PF⊥CB于点F,PE⊥CN于点E,
∵AB=AC=3,∠BAC=90°,
∴BC3,
∵BM=2CM,
∴2CM+CM=3,
∴CM,BM=CN=2,
∵∠ACB=∠ACN=45°,
∴∠MCN=2∠ACN=90°,
∴MN,
∵CA平分∠BCN,PF⊥CB于点F,PE⊥CN于点E,
∴PF=PE,
∴S△CPMCM PFCM PE,S△CPNCN PE,
∵,
∴,
∴PMMNMN,
故答案为:.
【点评】此题重点考查等腰直角三角形的性质、全等三角形的判定与性质、勾股定理、角平分线的性质、根据面积等式推导线段之间的数量关系等知识与方法,证明△ABM≌△ACN是解题的关键.
12.(2025 新蔡县三模)如图,Rt△ABC中,AC=BC=8,M为边BC的中点,长度为2的动线段AN绕点A旋转,连接MN,取MN的中点P,则CP长度的最大值为 21 ,最小值为 21 .
【考点】旋转的性质;等腰直角三角形.
【专题】等腰三角形与直角三角形;平移、旋转与对称;几何直观;应用意识.
【答案】21,21.
【分析】连接AM,取AM的中点Q,连接CQ,求出CMBC=4,AM4,可得CQAM=2,求出PQAN=1,知P在以Q为圆心,1为半径的圆上运动,即可得当P在线段CQ上时,CP最小为21;当P在CQ延长线上时,CP最大为21.
【解答】解:连接AM,取AM的中点Q,连接CQ,如图:
∵Rt△ABC,AC=BC=8,M为边BC的中点,
∴CMBC=4,AM4,
∵Q为AM中点,∠ACM=90°,
∴CQAM=2,
∵P为MN中点,Q为AM中点,
∴PQ是△AMN的中位线,
∴PQAN2=1,
∴P在以Q为圆心,1为半径的圆上运动,
当P在线段CQ上时,CP最小,如图:
此时CP最小为21;
当P在CQ延长线上时,CP最大,如图:
此时CP最大为21;
故答案为:21,21.
【点评】本题考查直角三角形中的旋转问题,解题的关键是求出P的轨迹.
13.(2025 金凤区校级二模)八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则直线l的解析式为 y .
【考点】中心对称;一次函数图象上点的坐标特征;待定系数法求一次函数解析式.
【专题】一次函数及其应用;运算能力.
【答案】y.
【分析】设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标即可得到该直线l的解析式.
【解答】解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC于C,
∵正方形的边长为1,
∴OB=3,
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴两边分别是4,
∴三角形ABO面积是5,
∴OB AB=5,
∴AB,
∴OC,
由此可知直线l经过(,3),
设直线方程为y=kx,
则3k,
k,
∴直线l解析式为yx.
故选:答案为:y.
【点评】此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,此题难度较大,解题的关键是作AB⊥y轴,作AC⊥x轴,根据题意即得到:直角三角形ABO,利用三角形的面积公式求出AB的长.
14.(2025 齐齐哈尔四模)如图,在平面直角坐标系中,AB=AC,∠BAC=120°,点A的坐标为(0,1),点B,C在x轴上,将△ABC绕顶点A旋转30°,得到△A1B1C1,则点C1的坐标为 或(2,1) .
【考点】坐标与图形变化﹣旋转;等腰三角形的性质;含30度角的直角三角形.
【专题】推理能力.
【答案】或(2,1).
【分析】先求出AC的长度,再分顺时针旋转和逆时针旋转两种情况,结合旋转的性质,利用三角函数求出点C1的坐标.
【解答】解:∵A(0,1),AB=AC,∠BAC=120°,AO⊥BC,
∴,AO=1.
在Rt△AOC中,
,即,
∴AC=2.
情况一:顺时针旋转30°,
∴∠CAC1=30°,
∴∠OAC1=∠CAO﹣∠CAC1=60°﹣30°=30°.
过C1作C1D⊥y轴于D点,
在Rt△AC1D中,
AC1=AC=2,,.
∴,.
∴,
∴C1坐标为.
情况二:逆时针旋转30°
过C1作C1D⊥x轴于D点,
则∠OAC1=∠CAO+∠CAC1=60°+30°=90°.
∵AC1=AC=2,A点坐标(0,1),
∴C1的横坐标为2,纵坐标为1,即C1坐标为(2,1).
故答案为:或(2,1).
【点评】本题主要考查旋转的性质,三角函数的计算,熟练掌握旋转的性质是解题的关键.
15.(2025 温州模拟)如图,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE,点B的对应点D恰好落在BC边上,若DE⊥AC,∠CAD=25°,则旋转角α的大小是 50 °.
【考点】旋转的性质.
【专题】平移、旋转与对称;运算能力.
【答案】50.
【分析】证明∠ABD=∠ADB=∠ADE=65°,可得结论.
【解答】解:设AC交DE于点O.
∵DE⊥AC,
∴∠AOD=90°,
∵∠CAD=25°,
∴∠ADE=90°﹣25°=65°,
∵AB=AD,
∴∠ABD=∠ADB=∠ADE=65°,
∴∠BAD=180°﹣65°﹣65°=50°.
故答案为:50.
【点评】本题考查旋转的性质,等腰三角形的性质,三角形内角和定理等知识,解题的关键是掌握旋转变换的性质,属于中考常考题型.
三.解答题(共5小题)
16.(2025 武汉)如图是由小正方形组成的3×4网格,每个小正方形的顶点叫作格点,矩形ABCD的四个顶点都是格点.仅用无刻度直尺在给定网格中完成如下两个问题,每个问题的画线不得超过五条.
(1)如图1,E是格点,先将点E绕点A逆时针旋转90°,画对应点F,再画直线FG交AB于点G,使直线FG平分矩形ABCD的面积.
(2)如图2,先画点C关于直线BD的对称点M,再画射线MN交BD于点N,使MN∥AD.
【考点】作图﹣旋转变换;平行线的判定;作图﹣轴对称变换.
【专题】作图题;几何直观.
【答案】见解析.
【分析】(1)利用旋转变换的性质作出点E的对应点F即可,连接AC交网格线于点O,作直线FO交AB于点G即可;
(2)取格点J,K,连接AK,CJ交于点M,取格点P,L,Q.网格线的中点T,连接PL,QT交于点W,作直线MW交BD于点N,直线MN即为所求.
【解答】解:(1)如图1中,点F,直线FG即为所求;
(2)如图,点M,直线MN即为所求.
【点评】本题考查作图﹣旋转变换,轴对称变换,平行线的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
17.(2025 青阳县模拟)如图,在由边长为1个单位长度的小正方形组成的网格中,建立平面直角坐标系,格点(网格线的交点)A,B,C的坐标分别为(2,5),(1,2),(5,3).
(1)将线段BC先向左平移3个单位长度,再向下平移4个单位长度,得到线段B1C1,画出线段B1C1;
(2)将线段AC绕O点逆时针旋转90°,得到线段A1C2,画出线段A1C2;
(3)在所给的网格图中确定一个格点D,使得线段AD平分线段BC,写出点D的坐标.
【考点】作图﹣旋转变换;作图﹣平移变换.
【专题】作图题;几何直观.
【答案】(1)(2)见解析;(3)见解析,D(4,0)或(6,﹣4).
【分析】(1)利用平移变换的性质分别作出B,C的对应点B1,C1即可;
(2)利用旋转变换的性质分别作出A,C的对应点A2,C2即可;
(3)构造平行四边形ABDC或AD的延长线上的点D′满足条件.
【解答】解:(1)如图所示,线段B1C1即为所求.
(2)如图所示,线段A1C2即为所求;
(3)如图所示,点D,点D′即为所求,D(4,0)或(6,﹣4).
【点评】本题考查作图﹣旋转变换,平移变换,解题的关键是掌握旋转变换,平移变换的性质.
18.(2025 广东模拟)如图,在Rt△ABC中,∠C=90°,将△ABC绕着点B逆时针旋转得到△FBE,点C,A的对应点分别为E,F.点E落在BA上,连接AF.
(1)若∠BAC=40°,求∠BAF的度数;
(2)若AC=8,BC=6,求AF的长.
【考点】旋转的性质;勾股定理.
【专题】平移、旋转与对称;推理能力.
【答案】见试题解答内容
【分析】(1)根据三角形的内角和定理得到∠ABC=50°,根据旋转的性质得到∠EBF=∠ABC=50°,AB=BF,根据三角形的内角和定理即可得到结论;
(2)根据勾股定理得到AB=10,根据旋转的性质得到BE=BC=6,EF=AC=8,根据勾股定理即可得到结论.
【解答】解:(1)在Rt△ABC中,∠C=90°,∠BAC=40°,
∴∠ABC=50°,
∵将△ABC绕着点B逆时针旋转得到△FBE,
∴∠EBF=∠ABC=50°,AB=BF,
∴∠BAF=∠BFA(180°﹣50°)=65°;
(2)∵∠C=90°,AC=8,BC=6,
∴AB=10,
∵将△ABC绕着点B逆时针旋转得到△FBE,
∴BE=BC=6,EF=AC=8,
∴AE=AB﹣BE=10﹣6=4,
∴AF4.
【点评】本题考查了旋转的性质,勾股定理,熟练掌握旋转的性质是解题的关键.
19.(2025 朝阳区校级模拟)如图,在矩形ABCD中,AB=5,BC=8,AE=3,点P沿AB﹣BC运动,将点P绕点E逆时针旋转90°得到点Q.
(1)EP平分矩形面积时,求BP的长;
(2)E、Q、C三点共线时,求AP的长;
(3)CQ的最小值为 2 ,点Q的路径长为 13 ;
(4)当点Q在四边形内形时,四边形PBCQ面积的最大值为 16 ,此时线段AP的长为 1 .
【考点】几何变换综合题.
【专题】配方法;图形的全等;矩形 菱形 正方形;运算能力;推理能力.
【答案】(1)5;
(2)3;
(3)2,13;
(4)16,1.
【分析】(1)连接AC,BD,交于点O,射线EO交BC于P,此时EP平分矩形ABCD的面积,根据对称性得出结果;
(2)可得出DE=CD=5,∠D=90°,从而得出∠QEF=∠DCE=45°,进而得出∠APE=∠AEP=45°,从而AP=AE=3;
(3)当点P在AB上时,作EG⊥AD,作QG⊥EG于G,GQ所在的直线交CD于Q′,可证得△AEP≌△GEQ,从而得出EG=AE=3,从而得出点Q在过点G且与AD的距离是3的线段上运动,当点P在B时,点Q在Q′处,进一步得出结果;当点P在BC上时,作EW⊥BC于W,可得出△EPW≌△EQD,进一步得出结果;
(4)作QV⊥AB于V,作QX⊥AD于X,设AP=x,设四边形PBCQ的面积为S,可得出AV=QX=3,VQ=AX=x+3,BV=2,PV=3﹣x,从而得出S的关系式,配方求得结果.
【解答】解:(1)如图1,
连接AC,BD,交于点O,射线EO交BC于P,
此时EP平分矩形ABCD的面积,
由对称性可得:BP=DE=AD﹣AE=6﹣3=5;
(2)如图2,
∵DE=CD=5,∠D=90°,
∴∠QEF=∠DCE=45°,
∵点P绕点E逆时针旋转90°得到点Q,
∴∠PEQ=90°,
∴∠AEP=90°﹣∠FEQ=45°,
∵∠A=90°,
∴∠APE=∠AEP=45°,
∴AP=AE=3;
(3)如图3﹣1,
当点P在AB上时,
作EG⊥AD,作QG⊥EG于G,GQ所在的直线交CD于Q′,
∴∠A=∠G=∠AEG=90°,
∴∠AEP+∠PEG=90°,∠QEG+∠PEG=90°,
∴∠AEP=∠QEG,
∵PE=EQ,
∴△AEP≌△GEQ(AAS),
∴EG=AE=3,
∴点Q在过点G且与AD的距离是3的线段上运动,
当点P在B时,点Q在Q′处,
此时CQ最小=2,GQ′=DE=5,
如图3﹣2,
当点P在BC上时,
作EW⊥BC于W,
同理可得,
△EPW≌△EQD,
∴点Q在直线CD上运动,
当点P在点C处时,点Q在Q″处,
DQ″=CD=5,
∴当点P从点B运动到C处,Q运动5+3=8,
∴点Q共运动5+8=13,
故答案为:2,13;
(4)如图4,
作QV⊥AB于V,作QX⊥AD于X,
设AP=x,设四边形PBCQ的面积为S,
由上知,
AV=QX=3,VQ=AX=x+3,BV=2,PV=3﹣x,
∴S=S△PQC+S梯形BCQV
,
∴当x=1时,S最大=16,
故答案为:16,1.
【点评】本题考查了矩形性质,全等三角形的判定和性质,配方法等知识,解决问题的关键是熟练掌握有关基础知识.
20.(2025 河南模拟)综合与实践:
定义:将三角形沿过顶点的直线折叠,折叠后的另一个顶点恰好落在这个三角形的边上(不含顶点)时,此时折痕被称为“落边折痕”.
特例感知:已知△ABC,D为AC边上一点,将△ABC沿BD折叠,使得点A恰好落在BC边上(不含点C),此时折痕BD称为“落边折痕”.
探究1:如图①,若△ABC是直角三角形,其中∠A=90°,∠ABC=60°,AB=1,若点D为AC边上一点,将△ABC沿着BD折叠后,点A恰好落在BC边上的点E处,求“落边折痕”BD的长;
探究2:如图②,若△ABC是等腰三角形,其中∠A=120°,请求出“落边折痕BD”将其分割后的△ABD与△BCD的面积比;
探究3:如图③,若△ABC是等腰三角形,其中AB=AC=5,BC=6,请求出其“落边折痕”的长度.
【考点】几何变换综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】探究1:;
探究2:;
探究3:或.
【分析】探究1:根据叠的性质可知,,则∴,即可求解;
探究2:分别过点D作AB、EB的垂线,垂足分别为M,N.根据折叠的性质可知,S△ABD=S△EBD,∠ABD=∠EBD,推出DM=DN,得到,即可求解;
探究3:分情况讨论:当沿BD折叠,点A落在BC边上的点E处时,当沿CH折叠,点A落在BC边上的点I处时,当沿BP折叠,点A落在AC边上的点Q处时,当沿CX折叠,点A落在AB边上的点Y处时,结合相关知识求解即可.
【解答】解:探究1:∵△ABC是直角三角形,∠ABC=60°,将△ABC沿着BD折叠后,点A恰好落在BC边上的点E处,
∴,
又∵∠A=90°,AB=1,
∴;
探究2:如图②,分别过点D作AB、EB的垂线,垂足分别为M,N.
∵△ABC是等腰三角形,其中∠A=120°,将△ABC沿着BD折叠后,点A恰好落在BC边上的点E处,
∴S△ABD=S△EBD,∠ABD=∠EBD,
∴DM=DN,
∴,(将面积比转化为线段比),
在等腰△ABC中,∠BAC=120°,
∴∠ABC=30°,
∴,
即;
探究3:根据题意可知,当三角形存在“落边折痕”时,折叠后的对应点在三角形的边上(不含顶点).
在等腰△ABC中,AB=AC=5,BC=6,BC>AB,
∴只能是点A向下折叠,则分情况讨论(若是其他折叠方式,则对应点落在三角形边的延长线上或顶点处,不满足定义);
①如图③,当沿BD折叠,点A落在BC边上的点E处时,
由探究2可得,,
∴,
过点D作DF⊥BC于点F,过点A作AG⊥BC于点G,(通过面积比,可以推导出对应线段比值,构造等量关系,求解所需线段),
∴,G为BC中点,AG∥DF,
∴CG=3,△AGC∽△DFC,
由勾股定理得:,
∴,
∴,,
∴,
∴,
在Rt△BDF中,;
②如图④,当沿CH折叠,点A落在BC边上的点I处时,同①,则;(此种情况与情况①属于对称状态,折痕相等);
③如图⑤,当沿BP折叠,点A落在AC边上的点Q处时,
BP为AQ的垂直平分线,即BP⊥AC,
由①可知,
∴,
∴;
④如图⑥,当沿CX折叠,点A落在AB边上的点Y处时,CX为AY的垂直平分线,则同情况③,则.(此种情况与情况③属于对称状态,折痕亦相等),
综上所述,“落边折痕”的长度为或.
【点评】本题属于几何变换综合题,主要考查了折叠的性质,解直角三角形,等腰三角形的性质,相似三角形的判定与性质,角平分线的性质,解题的关键是灵活运用相关知识.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年中考数学一轮复习 图形的旋转
一.选择题(共10小题)
1.(2025 永寿县校级模拟)下列图形中,不是轴对称图形,但是中心对称图形的是( )
A. B.
C. D.
2.(2025 大同模拟)科技馆是青少年科普实践的重要基地,通过互动性强的展览和活动,激发青少年的好奇心和探索精神.以下科技馆的标识中,文字上方的图案是中心对称图形的是( )
A.山西省科技馆 B.甘肃省科技馆
C.合肥市科技馆 D.滨州市科技馆
3.(2025 兴庆区校级一模)大约在两千四百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验,并在《墨经》中做了记载,如图,在实验中,物和像属于以下哪种变换( )
A.平移变换 B.对称变换 C.旋转变换 D.位似变换
4.(2025 大庆模拟)如图,△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交DE于点F,下列结论中不一定正确的是( )
A.∠ACD=∠EFB B.AC∥DE C.AB=DE D.BF⊥CE
5.(2025 蓬江区校级三模)如图,在菱形ABCD中,∠ABC=80°,将线段BA绕点B顺时针旋转到对角线BD上得到线段BE,则∠AED=( )
A.120° B.110° C.100° D.90°
6.(2025 金凤区模拟)如图,将一副直角三角尺的其中两个顶点重合叠放(∠A=30°,∠ABC=60°,∠D=∠BED=45°)三角尺ABC固定不动,将三角尺DBE绕点B转动.当DE∥BC时,∠ABE的度数为( )
A.75° B.60° C.105° D.75°或105°
7.(2025 新华区校级一模)如图,在Rt△ABC中,∠C=90°,∠ABC=66°,将△ABC绕点B逆时针旋转得到△A'BC',当点C′落在边AB上时,连接AA',则∠AA'C'=( )
A.24° B.33° C.43° D.57°
8.(2025 滨海新区校级模拟)如图,将△ABC绕点A顺时针旋转α,得到△ADE,点B,C的对应点分别为点D,E,若点B,E,D在一条直线上,连接EC,则下列说法正确的是( )
A.∠AEB+∠ACB=180° B.∠CBE=2α
C.AB=EB+BC D.AD=EC
9.(2025 济宁校级二模)如图,在平面直角坐标系中,四边形OABC为平行四边形,其中点O(0,0),A(3,4)C(8,0),以点O为圆心,OC的长为半径作弧,交AB于点D,再把线段OD绕点O逆时针旋转90°得到线段OD′,则点D′的坐标为( )
A.(﹣4,4) B.(﹣4,4) C.(4,﹣4) D.(4,﹣4)
10.(2025 青岛)如图,在平面直角坐标系中,点A,B,C都在格点上,将△ABC关于y轴的对称图形绕原点O旋转180°.得到△A1B1C1,则点A的对应点A1的坐标是( )
A.(﹣1,﹣2) B.(1,2) C.(2,1) D.(﹣2,﹣1)
二.填空题(共5小题)
11.(2025 花山区校级三模)如图,在Rt△BAC中,∠BAC=90°,AB=AC,点M在边BC上(不与点B,C重合),△AMN是以点A为直角顶点的等腰直角三角形,MN交AC于点P,连接CN.
(1)∠ACN的度数为 °;
(2)若AB=3,BM=2CM,则PM的长为 .
12.(2025 新蔡县三模)如图,Rt△ABC中,AC=BC=8,M为边BC的中点,长度为2的动线段AN绕点A旋转,连接MN,取MN的中点P,则CP长度的最大值为 ,最小值为 .
13.(2025 金凤区校级二模)八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则直线l的解析式为 .
14.(2025 齐齐哈尔四模)如图,在平面直角坐标系中,AB=AC,∠BAC=120°,点A的坐标为(0,1),点B,C在x轴上,将△ABC绕顶点A旋转30°,得到△A1B1C1,则点C1的坐标为 .
15.(2025 温州模拟)如图,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE,点B的对应点D恰好落在BC边上,若DE⊥AC,∠CAD=25°,则旋转角α的大小是 °.
三.解答题(共5小题)
16.(2025 武汉)如图是由小正方形组成的3×4网格,每个小正方形的顶点叫作格点,矩形ABCD的四个顶点都是格点.仅用无刻度直尺在给定网格中完成如下两个问题,每个问题的画线不得超过五条.
(1)如图1,E是格点,先将点E绕点A逆时针旋转90°,画对应点F,再画直线FG交AB于点G,使直线FG平分矩形ABCD的面积.
(2)如图2,先画点C关于直线BD的对称点M,再画射线MN交BD于点N,使MN∥AD.
17.(2025 青阳县模拟)如图,在由边长为1个单位长度的小正方形组成的网格中,建立平面直角坐标系,格点(网格线的交点)A,B,C的坐标分别为(2,5),(1,2),(5,3).
(1)将线段BC先向左平移3个单位长度,再向下平移4个单位长度,得到线段B1C1,画出线段B1C1;
(2)将线段AC绕O点逆时针旋转90°,得到线段A1C2,画出线段A1C2;
(3)在所给的网格图中确定一个格点D,使得线段AD平分线段BC,写出点D的坐标.
18.(2025 广东模拟)如图,在Rt△ABC中,∠C=90°,将△ABC绕着点B逆时针旋转得到△FBE,点C,A的对应点分别为E,F.点E落在BA上,连接AF.
(1)若∠BAC=40°,求∠BAF的度数;
(2)若AC=8,BC=6,求AF的长.
19.(2025 朝阳区校级模拟)如图,在矩形ABCD中,AB=5,BC=8,AE=3,点P沿AB﹣BC运动,将点P绕点E逆时针旋转90°得到点Q.
(1)EP平分矩形面积时,求BP的长;
(2)E、Q、C三点共线时,求AP的长;
(3)CQ的最小值为 ,点Q的路径长为 ;
(4)当点Q在四边形内形时,四边形PBCQ面积的最大值为 ,此时线段AP的长为 .
20.(2025 河南模拟)综合与实践:
定义:将三角形沿过顶点的直线折叠,折叠后的另一个顶点恰好落在这个三角形的边上(不含顶点)时,此时折痕被称为“落边折痕”.
特例感知:已知△ABC,D为AC边上一点,将△ABC沿BD折叠,使得点A恰好落在BC边上(不含点C),此时折痕BD称为“落边折痕”.
探究1:如图①,若△ABC是直角三角形,其中∠A=90°,∠ABC=60°,AB=1,若点D为AC边上一点,将△ABC沿着BD折叠后,点A恰好落在BC边上的点E处,求“落边折痕”BD的长;
探究2:如图②,若△ABC是等腰三角形,其中∠A=120°,请求出“落边折痕BD”将其分割后的△ABD与△BCD的面积比;
探究3:如图③,若△ABC是等腰三角形,其中AB=AC=5,BC=6,请求出其“落边折痕”的长度.
2026年中考数学一轮复习 图形的旋转
参考答案与试题解析
一.选择题(共10小题)
1.(2025 永寿县校级模拟)下列图形中,不是轴对称图形,但是中心对称图形的是( )
A. B.
C. D.
【考点】中心对称图形;轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.
【解答】解:A.该三角形既不是轴对称图形,也不是中心对称图形,故本选项不符合题意;
B.正方形是轴对称图形,也是中心对称图形,故本选项不符合题意;
C.正五边形是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.平行四边形不是轴对称图形,是中心对称图形,故本选项符合题意;
故选:D.
【点评】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
2.(2025 大同模拟)科技馆是青少年科普实践的重要基地,通过互动性强的展览和活动,激发青少年的好奇心和探索精神.以下科技馆的标识中,文字上方的图案是中心对称图形的是( )
A.山西省科技馆 B.甘肃省科技馆
C.合肥市科技馆 D.滨州市科技馆
【考点】中心对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】C
【分析】中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形可得答案.
【解答】解:A、选项图形不是中心对称图形,不符合题意;
B、选项图形不是中心对称图形,不符合题意;
C、选项图形是中心对称图形,符合题意;
D、选项图形不是中心对称图形,不符合题意.
故选:C.
【点评】本题主要考查了中心对称图形,掌握中心对称图形的定义是关键.
3.(2025 兴庆区校级一模)大约在两千四百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验,并在《墨经》中做了记载,如图,在实验中,物和像属于以下哪种变换( )
A.平移变换 B.对称变换 C.旋转变换 D.位似变换
【考点】几何变换的类型.
【专题】图形的相似;几何直观.
【答案】D
【分析】根据位似变换的定义判断即可.
【解答】解:小孔成倒像的实验,物和像属于位似变换.
故选:D.
【点评】本题考查几何变换的类型,平移变换,轴对称变换,旋转变换,位似变换等知识,解题的关键是理解各种变换的定义.
4.(2025 大庆模拟)如图,△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交DE于点F,下列结论中不一定正确的是( )
A.∠ACD=∠EFB B.AC∥DE C.AB=DE D.BF⊥CE
【考点】旋转的性质;平行线的判定.
【专题】平移、旋转与对称;几何直观.
【答案】B
【分析】设BF与CE相交于点G,由旋转得可得∠E=∠B=30°,AB=DE,∠BCE=∠ACD=60°,根据∠EGF=∠BGC,可得∠EFB=∠BCG=60°,则∠ACD=∠EFB.根据∠B=30°,∠BCG=60°,可得∠BGC=90°,即BF⊥CE.
【解答】解:设BF与CE相交于点G,
∵△ABC绕点C顺时针旋转60°得到△DEC,
∴∠E=∠B=30°,AB=DE,∠BCE=∠ACD=60°,
∵∠EGF=∠BGC,
∴∠EFB=∠BCG=60°,
∴∠ACD=∠EFB.
故A,C选项正确,不符合题意;
∵∠B=30°,∠BCG=60°,
∴∠BGC=90°,
∴BF⊥CE.
故D选项正确,不符合题意;
根据题意知条件不能得出AC∥DE,
故B选项不正确,符合题意.
故选:B.
【点评】本题考查旋转的性质、平行线的判定,熟练掌握旋转的性质是解答本题的关键.
5.(2025 蓬江区校级三模)如图,在菱形ABCD中,∠ABC=80°,将线段BA绕点B顺时针旋转到对角线BD上得到线段BE,则∠AED=( )
A.120° B.110° C.100° D.90°
【考点】旋转的性质;菱形的性质.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】先由菱形的性质得∠ABE=∠CBE∠ABC=40°,再由等腰三角形的性质和三角形内角和定理即可得出答案.
【解答】解:∵四边形ABCD是菱形,∠ABC=80°,
∴∠ABE=∠CBE∠ABC=40°,
∵BA=BE,
∴∠BAE=∠BEA(180°﹣40°)=70°,
∴∠AED=180°﹣∠AEB=110°,
故选:B.
【点评】本题考查了菱形的性质、等腰三角形的性质以及三角形内角和定理,熟练掌握菱形的性质和等腰三角形的性质是解题的关键.
6.(2025 金凤区模拟)如图,将一副直角三角尺的其中两个顶点重合叠放(∠A=30°,∠ABC=60°,∠D=∠BED=45°)三角尺ABC固定不动,将三角尺DBE绕点B转动.当DE∥BC时,∠ABE的度数为( )
A.75° B.60° C.105° D.75°或105°
【考点】旋转的性质;平行线的性质.
【专题】平移、旋转与对称;几何直观;推理能力.
【答案】D
【分析】分两种情况,运用平行线的性质求解即可.
【解答】解:如图①,
∵DE∥BC,
∴∠CBD=∠D=45°,
∴∠ABD=∠ABC﹣∠CBD=60°﹣45°=15°,
∵∠DBE=90°,
∴∠ABE=∠DBE﹣∠ABD=90°﹣15°=75°,
如图②,当DE∥BC时,
∵DE∥BC,
∴∠CBE=∠E=45°,
∴∠ABE=∠ABC+∠CBE=60°+45°=105°.
综上所述,∠ABE的度数为75°或105°,
故选:D.
【点评】本题主要考查了旋转的性质发,平行线的性质,解答本题的关键是熟练掌握旋转的性质.
7.(2025 新华区校级一模)如图,在Rt△ABC中,∠C=90°,∠ABC=66°,将△ABC绕点B逆时针旋转得到△A'BC',当点C′落在边AB上时,连接AA',则∠AA'C'=( )
A.24° B.33° C.43° D.57°
【考点】旋转的性质.
【专题】等腰三角形与直角三角形;平移、旋转与对称;推理能力.
【答案】B
【分析】由旋转的性质可得AB=A'B,∠ABC=66°=∠A'BC',∠C=90°=∠A'C'B,由等腰三角形的性质可得∠BAA'=57°,即可求解.
【解答】解:∵将△ABC绕点B逆时针旋转得到△A'BC',
∴AB=A'B,∠ABC=66°=∠A'BC',∠C=90°=∠A'C'B,
∴∠BAA'=57°,
∴∠AA'C'=33°,
故选:B.
【点评】本题考查了旋转的性质,等腰三角形的性质,掌握旋转的性质是解题的关键.
8.(2025 滨海新区校级模拟)如图,将△ABC绕点A顺时针旋转α,得到△ADE,点B,C的对应点分别为点D,E,若点B,E,D在一条直线上,连接EC,则下列说法正确的是( )
A.∠AEB+∠ACB=180° B.∠CBE=2α
C.AB=EB+BC D.AD=EC
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】由旋转的性质得到△ADE≌△ABC,推出∠AED=∠ACB,由邻补角的性质得到∠AEB+∠AED=180°,推出∠AEB+∠ACB=180°,由全等三角形的性质推出∠ABC=∠D,AD=AB,由等腰三角形的性质得到∠ABD=∠D,而∠BAD=α,求出∠D+∠ABD=(180°﹣α),得到EBC=180°﹣α,由全等三角形的性质得到DE=BC,因此EB+BC=DB,判定AB不一定等于EB+BC,由△ADE≌△ABC,推出AD=AB,得到AD和CE不一定相等.
【解答】解:由旋转的性质得到:△ADE≌△ABC,
∴∠AED=∠ACB,
∵∠AEB+∠AED=180°,
∴∠AEB+∠ACB=180°,
故A符合题意;
∵△ADE≌△ABC,
∴∠ABC=∠D,AD=AB,
∴∠ABD=∠D,
由旋转的性质得到:∠BAD=α,
∴∠D+∠ABD=(180°﹣α),
∴EBC=∠ABD+∠ABC=∠ABD+∠D=180°﹣α,
故B不符合题意;
∵△ADE≌△ABC,
∴DE=BC,
∴EB+BC=BE+DE=DB,
∵DE不一定等于AB,
∴AB不一定等于EB+BC,
故C不符合题意;
∵△ADE≌△ABC,
∴AD=AB,
∵AB和CE不一定相等,
∴AD和CE不一定相等,
故D不符合题意.
故选:A.
【点评】本题考查旋转的性质,关键是由旋转的性质得到△ADE≌△ABC,∠BAD=α.
9.(2025 济宁校级二模)如图,在平面直角坐标系中,四边形OABC为平行四边形,其中点O(0,0),A(3,4)C(8,0),以点O为圆心,OC的长为半径作弧,交AB于点D,再把线段OD绕点O逆时针旋转90°得到线段OD′,则点D′的坐标为( )
A.(﹣4,4) B.(﹣4,4) C.(4,﹣4) D.(4,﹣4)
【考点】坐标与图形变化﹣旋转;全等三角形的判定与性质;平行四边形的性质;旋转的性质.
【专题】平面直角坐标系;图形的全等;多边形与平行四边形;运算能力.
【答案】A
【分析】如图,延长BA交y轴于点E,过点D′作D′F⊥x轴于点F.证明△ODE≌△OD′F(AAS),推出D′F=DE=4,OF=OE=4可得结论.
【解答】解:如图,延长BA交y轴于点E,过点D′作D′F⊥x轴于点F.
由题意,可知DE⊥y轴,AE=3,OE=4.由旋转的性质,可知OD=OC=8,
∴DE4,
∵OD=OD′,∠DOD′=90°,
∴∠EOD+∠EOD′=90°,
∵∠D′OF+∠EOD′=90°.
∴∠D′OE=∠DOE,
∵∠DEO=∠D′FO=90°,
∴△ODE≌△OD′F(AAS),
∴D′F=DE=4,OF=OE=4.
∴点D′的坐标为(﹣4,4),
故选:A.
【点评】本题考查坐标与图形性质,全等三角形的判定和性质,平行四边形的性质,旋转的性质,解题的关键是学会添加常用辅助线,正确寻找全等三角形解决问题.
10.(2025 青岛)如图,在平面直角坐标系中,点A,B,C都在格点上,将△ABC关于y轴的对称图形绕原点O旋转180°.得到△A1B1C1,则点A的对应点A1的坐标是( )
A.(﹣1,﹣2) B.(1,2) C.(2,1) D.(﹣2,﹣1)
【考点】坐标与图形变化﹣旋转;关于x轴、y轴对称的点的坐标.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】先根据图中△ABC的位置求出点A的坐标,再根据关于y轴的对称可求解点A2,再根据绕原点O旋转180°即可求解点A1的坐标.
【解答】解:在平面直角坐标系中,点A(﹣1,2),
∴点A关于y轴对称的点A2(1,2),
将点A2(1,2)绕原点O旋转180°,
∴如图,点A1(﹣1,﹣2).
故选:A.
【点评】本题考查了平面直角坐标系中点的变换,熟练掌握点的对称与旋转是解决本题的关键.
二.填空题(共5小题)
11.(2025 花山区校级三模)如图,在Rt△BAC中,∠BAC=90°,AB=AC,点M在边BC上(不与点B,C重合),△AMN是以点A为直角顶点的等腰直角三角形,MN交AC于点P,连接CN.
(1)∠ACN的度数为 45 °;
(2)若AB=3,BM=2CM,则PM的长为 .
【考点】旋转的性质;全等三角形的判定与性质;勾股定理;等腰直角三角形.
【专题】图形的全等;等腰三角形与直角三角形;运算能力;推理能力.
【答案】(1)45;
(2).
【分析】(1)由旋转得AM=AN,∠MAN=90°,因为AB=AC,∠BAC=90°,所以∠B=∠ACB=45°,∠BAM=∠CAN=90°﹣∠CAM,可根据“SAS”证明△ABM≌△ACN,得∠B=∠ACN=45°,于是得到问题的答案;
(2)作PF⊥CB于点F,PE⊥CN于点E,由AB=AC=3,求得BC=3,由BM=2CM,求得CM,BM=CN=2,因为∠MCN=90°,所以MN,由角平分线的性质得PF=PE,则S△CPMCM PE,S△CPNCN PE,所以,则PMMN,于是得到问题的答案.
【解答】解:(1)∵△AMN是以点A为直角顶点的等腰直角三角形,
∴AM=AN,∠MAN=90°,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,∠BAM=∠CAN=90°﹣∠CAM,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(SAS),
∴∠B=∠ACN=45°,
故答案为:45.
(2)作PF⊥CB于点F,PE⊥CN于点E,
∵AB=AC=3,∠BAC=90°,
∴BC3,
∵BM=2CM,
∴2CM+CM=3,
∴CM,BM=CN=2,
∵∠ACB=∠ACN=45°,
∴∠MCN=2∠ACN=90°,
∴MN,
∵CA平分∠BCN,PF⊥CB于点F,PE⊥CN于点E,
∴PF=PE,
∴S△CPMCM PFCM PE,S△CPNCN PE,
∵,
∴,
∴PMMNMN,
故答案为:.
【点评】此题重点考查等腰直角三角形的性质、全等三角形的判定与性质、勾股定理、角平分线的性质、根据面积等式推导线段之间的数量关系等知识与方法,证明△ABM≌△ACN是解题的关键.
12.(2025 新蔡县三模)如图,Rt△ABC中,AC=BC=8,M为边BC的中点,长度为2的动线段AN绕点A旋转,连接MN,取MN的中点P,则CP长度的最大值为 21 ,最小值为 21 .
【考点】旋转的性质;等腰直角三角形.
【专题】等腰三角形与直角三角形;平移、旋转与对称;几何直观;应用意识.
【答案】21,21.
【分析】连接AM,取AM的中点Q,连接CQ,求出CMBC=4,AM4,可得CQAM=2,求出PQAN=1,知P在以Q为圆心,1为半径的圆上运动,即可得当P在线段CQ上时,CP最小为21;当P在CQ延长线上时,CP最大为21.
【解答】解:连接AM,取AM的中点Q,连接CQ,如图:
∵Rt△ABC,AC=BC=8,M为边BC的中点,
∴CMBC=4,AM4,
∵Q为AM中点,∠ACM=90°,
∴CQAM=2,
∵P为MN中点,Q为AM中点,
∴PQ是△AMN的中位线,
∴PQAN2=1,
∴P在以Q为圆心,1为半径的圆上运动,
当P在线段CQ上时,CP最小,如图:
此时CP最小为21;
当P在CQ延长线上时,CP最大,如图:
此时CP最大为21;
故答案为:21,21.
【点评】本题考查直角三角形中的旋转问题,解题的关键是求出P的轨迹.
13.(2025 金凤区校级二模)八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则直线l的解析式为 y .
【考点】中心对称;一次函数图象上点的坐标特征;待定系数法求一次函数解析式.
【专题】一次函数及其应用;运算能力.
【答案】y.
【分析】设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标即可得到该直线l的解析式.
【解答】解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC于C,
∵正方形的边长为1,
∴OB=3,
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴两边分别是4,
∴三角形ABO面积是5,
∴OB AB=5,
∴AB,
∴OC,
由此可知直线l经过(,3),
设直线方程为y=kx,
则3k,
k,
∴直线l解析式为yx.
故选:答案为:y.
【点评】此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,此题难度较大,解题的关键是作AB⊥y轴,作AC⊥x轴,根据题意即得到:直角三角形ABO,利用三角形的面积公式求出AB的长.
14.(2025 齐齐哈尔四模)如图,在平面直角坐标系中,AB=AC,∠BAC=120°,点A的坐标为(0,1),点B,C在x轴上,将△ABC绕顶点A旋转30°,得到△A1B1C1,则点C1的坐标为 或(2,1) .
【考点】坐标与图形变化﹣旋转;等腰三角形的性质;含30度角的直角三角形.
【专题】推理能力.
【答案】或(2,1).
【分析】先求出AC的长度,再分顺时针旋转和逆时针旋转两种情况,结合旋转的性质,利用三角函数求出点C1的坐标.
【解答】解:∵A(0,1),AB=AC,∠BAC=120°,AO⊥BC,
∴,AO=1.
在Rt△AOC中,
,即,
∴AC=2.
情况一:顺时针旋转30°,
∴∠CAC1=30°,
∴∠OAC1=∠CAO﹣∠CAC1=60°﹣30°=30°.
过C1作C1D⊥y轴于D点,
在Rt△AC1D中,
AC1=AC=2,,.
∴,.
∴,
∴C1坐标为.
情况二:逆时针旋转30°
过C1作C1D⊥x轴于D点,
则∠OAC1=∠CAO+∠CAC1=60°+30°=90°.
∵AC1=AC=2,A点坐标(0,1),
∴C1的横坐标为2,纵坐标为1,即C1坐标为(2,1).
故答案为:或(2,1).
【点评】本题主要考查旋转的性质,三角函数的计算,熟练掌握旋转的性质是解题的关键.
15.(2025 温州模拟)如图,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE,点B的对应点D恰好落在BC边上,若DE⊥AC,∠CAD=25°,则旋转角α的大小是 50 °.
【考点】旋转的性质.
【专题】平移、旋转与对称;运算能力.
【答案】50.
【分析】证明∠ABD=∠ADB=∠ADE=65°,可得结论.
【解答】解:设AC交DE于点O.
∵DE⊥AC,
∴∠AOD=90°,
∵∠CAD=25°,
∴∠ADE=90°﹣25°=65°,
∵AB=AD,
∴∠ABD=∠ADB=∠ADE=65°,
∴∠BAD=180°﹣65°﹣65°=50°.
故答案为:50.
【点评】本题考查旋转的性质,等腰三角形的性质,三角形内角和定理等知识,解题的关键是掌握旋转变换的性质,属于中考常考题型.
三.解答题(共5小题)
16.(2025 武汉)如图是由小正方形组成的3×4网格,每个小正方形的顶点叫作格点,矩形ABCD的四个顶点都是格点.仅用无刻度直尺在给定网格中完成如下两个问题,每个问题的画线不得超过五条.
(1)如图1,E是格点,先将点E绕点A逆时针旋转90°,画对应点F,再画直线FG交AB于点G,使直线FG平分矩形ABCD的面积.
(2)如图2,先画点C关于直线BD的对称点M,再画射线MN交BD于点N,使MN∥AD.
【考点】作图﹣旋转变换;平行线的判定;作图﹣轴对称变换.
【专题】作图题;几何直观.
【答案】见解析.
【分析】(1)利用旋转变换的性质作出点E的对应点F即可,连接AC交网格线于点O,作直线FO交AB于点G即可;
(2)取格点J,K,连接AK,CJ交于点M,取格点P,L,Q.网格线的中点T,连接PL,QT交于点W,作直线MW交BD于点N,直线MN即为所求.
【解答】解:(1)如图1中,点F,直线FG即为所求;
(2)如图,点M,直线MN即为所求.
【点评】本题考查作图﹣旋转变换,轴对称变换,平行线的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
17.(2025 青阳县模拟)如图,在由边长为1个单位长度的小正方形组成的网格中,建立平面直角坐标系,格点(网格线的交点)A,B,C的坐标分别为(2,5),(1,2),(5,3).
(1)将线段BC先向左平移3个单位长度,再向下平移4个单位长度,得到线段B1C1,画出线段B1C1;
(2)将线段AC绕O点逆时针旋转90°,得到线段A1C2,画出线段A1C2;
(3)在所给的网格图中确定一个格点D,使得线段AD平分线段BC,写出点D的坐标.
【考点】作图﹣旋转变换;作图﹣平移变换.
【专题】作图题;几何直观.
【答案】(1)(2)见解析;(3)见解析,D(4,0)或(6,﹣4).
【分析】(1)利用平移变换的性质分别作出B,C的对应点B1,C1即可;
(2)利用旋转变换的性质分别作出A,C的对应点A2,C2即可;
(3)构造平行四边形ABDC或AD的延长线上的点D′满足条件.
【解答】解:(1)如图所示,线段B1C1即为所求.
(2)如图所示,线段A1C2即为所求;
(3)如图所示,点D,点D′即为所求,D(4,0)或(6,﹣4).
【点评】本题考查作图﹣旋转变换,平移变换,解题的关键是掌握旋转变换,平移变换的性质.
18.(2025 广东模拟)如图,在Rt△ABC中,∠C=90°,将△ABC绕着点B逆时针旋转得到△FBE,点C,A的对应点分别为E,F.点E落在BA上,连接AF.
(1)若∠BAC=40°,求∠BAF的度数;
(2)若AC=8,BC=6,求AF的长.
【考点】旋转的性质;勾股定理.
【专题】平移、旋转与对称;推理能力.
【答案】见试题解答内容
【分析】(1)根据三角形的内角和定理得到∠ABC=50°,根据旋转的性质得到∠EBF=∠ABC=50°,AB=BF,根据三角形的内角和定理即可得到结论;
(2)根据勾股定理得到AB=10,根据旋转的性质得到BE=BC=6,EF=AC=8,根据勾股定理即可得到结论.
【解答】解:(1)在Rt△ABC中,∠C=90°,∠BAC=40°,
∴∠ABC=50°,
∵将△ABC绕着点B逆时针旋转得到△FBE,
∴∠EBF=∠ABC=50°,AB=BF,
∴∠BAF=∠BFA(180°﹣50°)=65°;
(2)∵∠C=90°,AC=8,BC=6,
∴AB=10,
∵将△ABC绕着点B逆时针旋转得到△FBE,
∴BE=BC=6,EF=AC=8,
∴AE=AB﹣BE=10﹣6=4,
∴AF4.
【点评】本题考查了旋转的性质,勾股定理,熟练掌握旋转的性质是解题的关键.
19.(2025 朝阳区校级模拟)如图,在矩形ABCD中,AB=5,BC=8,AE=3,点P沿AB﹣BC运动,将点P绕点E逆时针旋转90°得到点Q.
(1)EP平分矩形面积时,求BP的长;
(2)E、Q、C三点共线时,求AP的长;
(3)CQ的最小值为 2 ,点Q的路径长为 13 ;
(4)当点Q在四边形内形时,四边形PBCQ面积的最大值为 16 ,此时线段AP的长为 1 .
【考点】几何变换综合题.
【专题】配方法;图形的全等;矩形 菱形 正方形;运算能力;推理能力.
【答案】(1)5;
(2)3;
(3)2,13;
(4)16,1.
【分析】(1)连接AC,BD,交于点O,射线EO交BC于P,此时EP平分矩形ABCD的面积,根据对称性得出结果;
(2)可得出DE=CD=5,∠D=90°,从而得出∠QEF=∠DCE=45°,进而得出∠APE=∠AEP=45°,从而AP=AE=3;
(3)当点P在AB上时,作EG⊥AD,作QG⊥EG于G,GQ所在的直线交CD于Q′,可证得△AEP≌△GEQ,从而得出EG=AE=3,从而得出点Q在过点G且与AD的距离是3的线段上运动,当点P在B时,点Q在Q′处,进一步得出结果;当点P在BC上时,作EW⊥BC于W,可得出△EPW≌△EQD,进一步得出结果;
(4)作QV⊥AB于V,作QX⊥AD于X,设AP=x,设四边形PBCQ的面积为S,可得出AV=QX=3,VQ=AX=x+3,BV=2,PV=3﹣x,从而得出S的关系式,配方求得结果.
【解答】解:(1)如图1,
连接AC,BD,交于点O,射线EO交BC于P,
此时EP平分矩形ABCD的面积,
由对称性可得:BP=DE=AD﹣AE=6﹣3=5;
(2)如图2,
∵DE=CD=5,∠D=90°,
∴∠QEF=∠DCE=45°,
∵点P绕点E逆时针旋转90°得到点Q,
∴∠PEQ=90°,
∴∠AEP=90°﹣∠FEQ=45°,
∵∠A=90°,
∴∠APE=∠AEP=45°,
∴AP=AE=3;
(3)如图3﹣1,
当点P在AB上时,
作EG⊥AD,作QG⊥EG于G,GQ所在的直线交CD于Q′,
∴∠A=∠G=∠AEG=90°,
∴∠AEP+∠PEG=90°,∠QEG+∠PEG=90°,
∴∠AEP=∠QEG,
∵PE=EQ,
∴△AEP≌△GEQ(AAS),
∴EG=AE=3,
∴点Q在过点G且与AD的距离是3的线段上运动,
当点P在B时,点Q在Q′处,
此时CQ最小=2,GQ′=DE=5,
如图3﹣2,
当点P在BC上时,
作EW⊥BC于W,
同理可得,
△EPW≌△EQD,
∴点Q在直线CD上运动,
当点P在点C处时,点Q在Q″处,
DQ″=CD=5,
∴当点P从点B运动到C处,Q运动5+3=8,
∴点Q共运动5+8=13,
故答案为:2,13;
(4)如图4,
作QV⊥AB于V,作QX⊥AD于X,
设AP=x,设四边形PBCQ的面积为S,
由上知,
AV=QX=3,VQ=AX=x+3,BV=2,PV=3﹣x,
∴S=S△PQC+S梯形BCQV
,
∴当x=1时,S最大=16,
故答案为:16,1.
【点评】本题考查了矩形性质,全等三角形的判定和性质,配方法等知识,解决问题的关键是熟练掌握有关基础知识.
20.(2025 河南模拟)综合与实践:
定义:将三角形沿过顶点的直线折叠,折叠后的另一个顶点恰好落在这个三角形的边上(不含顶点)时,此时折痕被称为“落边折痕”.
特例感知:已知△ABC,D为AC边上一点,将△ABC沿BD折叠,使得点A恰好落在BC边上(不含点C),此时折痕BD称为“落边折痕”.
探究1:如图①,若△ABC是直角三角形,其中∠A=90°,∠ABC=60°,AB=1,若点D为AC边上一点,将△ABC沿着BD折叠后,点A恰好落在BC边上的点E处,求“落边折痕”BD的长;
探究2:如图②,若△ABC是等腰三角形,其中∠A=120°,请求出“落边折痕BD”将其分割后的△ABD与△BCD的面积比;
探究3:如图③,若△ABC是等腰三角形,其中AB=AC=5,BC=6,请求出其“落边折痕”的长度.
【考点】几何变换综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】探究1:;
探究2:;
探究3:或.
【分析】探究1:根据叠的性质可知,,则∴,即可求解;
探究2:分别过点D作AB、EB的垂线,垂足分别为M,N.根据折叠的性质可知,S△ABD=S△EBD,∠ABD=∠EBD,推出DM=DN,得到,即可求解;
探究3:分情况讨论:当沿BD折叠,点A落在BC边上的点E处时,当沿CH折叠,点A落在BC边上的点I处时,当沿BP折叠,点A落在AC边上的点Q处时,当沿CX折叠,点A落在AB边上的点Y处时,结合相关知识求解即可.
【解答】解:探究1:∵△ABC是直角三角形,∠ABC=60°,将△ABC沿着BD折叠后,点A恰好落在BC边上的点E处,
∴,
又∵∠A=90°,AB=1,
∴;
探究2:如图②,分别过点D作AB、EB的垂线,垂足分别为M,N.
∵△ABC是等腰三角形,其中∠A=120°,将△ABC沿着BD折叠后,点A恰好落在BC边上的点E处,
∴S△ABD=S△EBD,∠ABD=∠EBD,
∴DM=DN,
∴,(将面积比转化为线段比),
在等腰△ABC中,∠BAC=120°,
∴∠ABC=30°,
∴,
即;
探究3:根据题意可知,当三角形存在“落边折痕”时,折叠后的对应点在三角形的边上(不含顶点).
在等腰△ABC中,AB=AC=5,BC=6,BC>AB,
∴只能是点A向下折叠,则分情况讨论(若是其他折叠方式,则对应点落在三角形边的延长线上或顶点处,不满足定义);
①如图③,当沿BD折叠,点A落在BC边上的点E处时,
由探究2可得,,
∴,
过点D作DF⊥BC于点F,过点A作AG⊥BC于点G,(通过面积比,可以推导出对应线段比值,构造等量关系,求解所需线段),
∴,G为BC中点,AG∥DF,
∴CG=3,△AGC∽△DFC,
由勾股定理得:,
∴,
∴,,
∴,
∴,
在Rt△BDF中,;
②如图④,当沿CH折叠,点A落在BC边上的点I处时,同①,则;(此种情况与情况①属于对称状态,折痕相等);
③如图⑤,当沿BP折叠,点A落在AC边上的点Q处时,
BP为AQ的垂直平分线,即BP⊥AC,
由①可知,
∴,
∴;
④如图⑥,当沿CX折叠,点A落在AB边上的点Y处时,CX为AY的垂直平分线,则同情况③,则.(此种情况与情况③属于对称状态,折痕亦相等),
综上所述,“落边折痕”的长度为或.
【点评】本题属于几何变换综合题,主要考查了折叠的性质,解直角三角形,等腰三角形的性质,相似三角形的判定与性质,角平分线的性质,解题的关键是灵活运用相关知识.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
