辽宁省鞍山市2024-2025学年高一下学期期末考试物理试卷(含答案)
文档属性
| 名称 | 辽宁省鞍山市2024-2025学年高一下学期期末考试物理试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 667.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-10 12:41:53 | ||
图片预览




文档简介
辽宁省鞍山市2024-2025学年高一下学期期末考试物理试卷
一、单选题
1.关于运动和力,下列说法正确的是( )
A.物体受到的力不为恒力,物体一定做曲线运动
B.物体受到变化的合力作用时,它的速度大小一定改变
C.物体在不垂直于速度方向的合力作用下,速度大小可能一直不变
D.当物体受到与初速度方向不在同一条直线的合力作用时,物体一定做曲线运动
2.如图为直升飞机吊装全地形车的情景,飞机水平匀速飞行的同时把全地形车往上提升,让全地形车竖直向上做匀加速直线运动。若以全地形车刚开始向上运动的位置为坐标原点,竖直向上为y轴正方向,飞机飞行方向为x轴正方向,则全地形车的运动轨迹为( )
A.B.C. D.
3.我国北斗卫星导航系统(BDS)可以为全球提供定位、导航、授时、5G传输等服务。A、B为“北斗”系统中的两颗卫星,这两颗卫星均绕地球做匀速圆周运动。A、B两颗卫星在轨运行周期之比为k,则A、B两颗卫星与地心连线在单位时间内扫过的面积之比为( )
A.k B. C. D.
4.2024年第11号台风“摩羯”于9月6日在海南文昌登陆,登陆时中心附近最大风力有17级以上,造成具大破坏.已知11级台风的风速范围为,17级台风的风速范围为.若台风迎面垂直吹向一固定的交通标志牌,则17级台风对该标志牌的作用力大小约为11级台风的( )
A.2倍 B.4倍 C.8倍 D.16倍
5.如图所示,楔形木块固定在水平面上,光滑斜面与水平面的夹角为60°,粗糙斜面与水平面的夹角为30°,与均足够长。长为l、质量为m、粗细均匀、质量分布均匀的软绳放置于上,其上端与B齐平。质量为2m的物块通过一根不计质量的细线与软绳上端相连,并放置于上,物块由静止释放后沿下滑(重力加速度为g),直到软绳刚好离开完全进入,在此过程中( )
A.物块和软绳组成的系统机械能守恒
B.软绳的重力势能减少
C.物块的重力势能减少
D.软绳克服摩擦力做的功等于软绳的机械能减少量
6.2024年9月24日,我国全球首个医学遥感卫星(珞珈四号01星)成功发射,卫星在离地面约的高度绕地球做匀速圆周运动;2022年4月15日,我国新一代地球同步轨道通信卫星(中星卫星)成功发射,卫星在离地面约的高度绕地球做匀速圆周运动;地球赤道上有一物体。关于赤道上物体、珞珈四号01星、中星卫星,下列说法正确的是( )
A.赤道上物体的线速度最大
B.赤道上物体的周期小于中星卫星的周期
C.珞珈四号01星的角速度小于中星6D卫星的角速度
D.珞珈四号01星的向心加速度大于中星卫星的向心加速度
7.如图所示,光滑水平面上甲、乙两球间粘少许炸药,一起以速度0.5 m/s向右做匀速直线运动。已知甲、乙两球质量分别为0.1 kg和0.2 kg。某时刻炸药突然爆炸,分开后两球仍沿原直线运动,从爆炸开始计时经过3.0 s,两球之间的距离为x = 2.7 m,则说法正确的是( )
A.刚分离时,甲、乙两球的速度方向相同
B.刚分离时,甲球的速度大小为0.1 m/s,方向水平向左
C.刚分离时,乙球的速度大小为0.3 m/s
D.爆炸过程中释放的能量为0.27 J
二、多选题
8.水车是中国最古老的农业灌溉工具,是珍贵的历史文化遗产。水车的简易模型如图所示,水流自水平放置的水管流出,水流轨迹与水车车轮的边缘相切,可使车轮持续转动,切点与所在车轮横截面的圆心的连线与水平方向的夹角为。若水管出水口处水流的速度大小为,车轮半径,不计空气阻力,重力加速度大小取0.8,水流到达车轮边缘时的速度与车轮边缘切点的线速度相同,则下列说法正确的是( )
A.水管出水口距轮轴的水平距离为
B.水管出水口距轮轴的竖直距离为
C.车轮的角速度是
D.从出水口到车轮边缘的过程中,水流速度变化量的大小为
9.我国首次火星探测任务已取得圆满成功。着陆器着陆前的模拟轨迹如图所示,先在轨道I上运动,经过点启动变轨发动机切换到圆轨道II上运动,经过一段时间后,再次经过点时启动变轨发动机切换到圆轨道III上运动。轨道上的三点与火星中心位于同一直线上,两点分别是椭圆轨道的远火星点和近火星点,且(R为火星的半径)。着陆器在轨道I、Ⅱ、III上经过点的速度分别为,在轨道Ⅱ上的运行周期为,引力常量为,下列说法正确的是( )
A.
B.火星的密度为
C.着陆器变轨前在轨道I上运动时,经过点的加速度为
D.着陆器在轨道Ⅱ上经过点的机械能小于轨道III上经过点的机械能
10.中国目前拥有世界上最完善的高铁系统,高铁是中国科技发展的一张世界名片。假设有一动车组由四节车厢连接而成,每节车厢的质量均为、阻力均恒为,其中第一节和第四节为动力车厢,功率均恒为P,重力加速度为g。该动车组由静止开始恒定功率启动,下列说法正确的是( )
A.该动车组的最大行驶速度为
B.由静止到最大速度过程的平均速度为
C.该动车组速度达到最大时,第二、三两节车厢之间的作用力大小为
D.当速度为最大值的一半时,动车组运行的加速度大小为
11.某学习小组采用如图所示的装置验证滑块碰撞过程中的动量守恒。
(1)用天平测得滑块A、B(均包括挡光片)的质量分别为、。
(2)接通充气泵电源后,导轨左侧放一滑块并推动滑块,滑块通过两个光电门时,与光电门1、2相连的计时器测得的挡光时间分别为0.07s、0.06s,则应将导轨右端 (选填“调高”或“调低”),直至滑块通过两个光电门的 ,说明气垫导轨已经调节水平。
(3)滑块B放在两个光电门之间,滑块A向左挤压导轨架上的弹片后释放滑块A,碰后滑块A、B均一直向右运动。与光电门1相连的计时器的示数只有一个,为,与光电门2相连的计时器的示数有两个,先后为、。
(4)已知两挡光片的宽度相同,在实验误差允许的范围内,若等式 (用测得的物理量表示)成立,说明滑块A、B碰撞过程中动量守恒;若表达式 (仅用t1、t2和t3表示)成立,说明滑块A、B碰撞过程中机械能和动量均守恒。
四、实验题
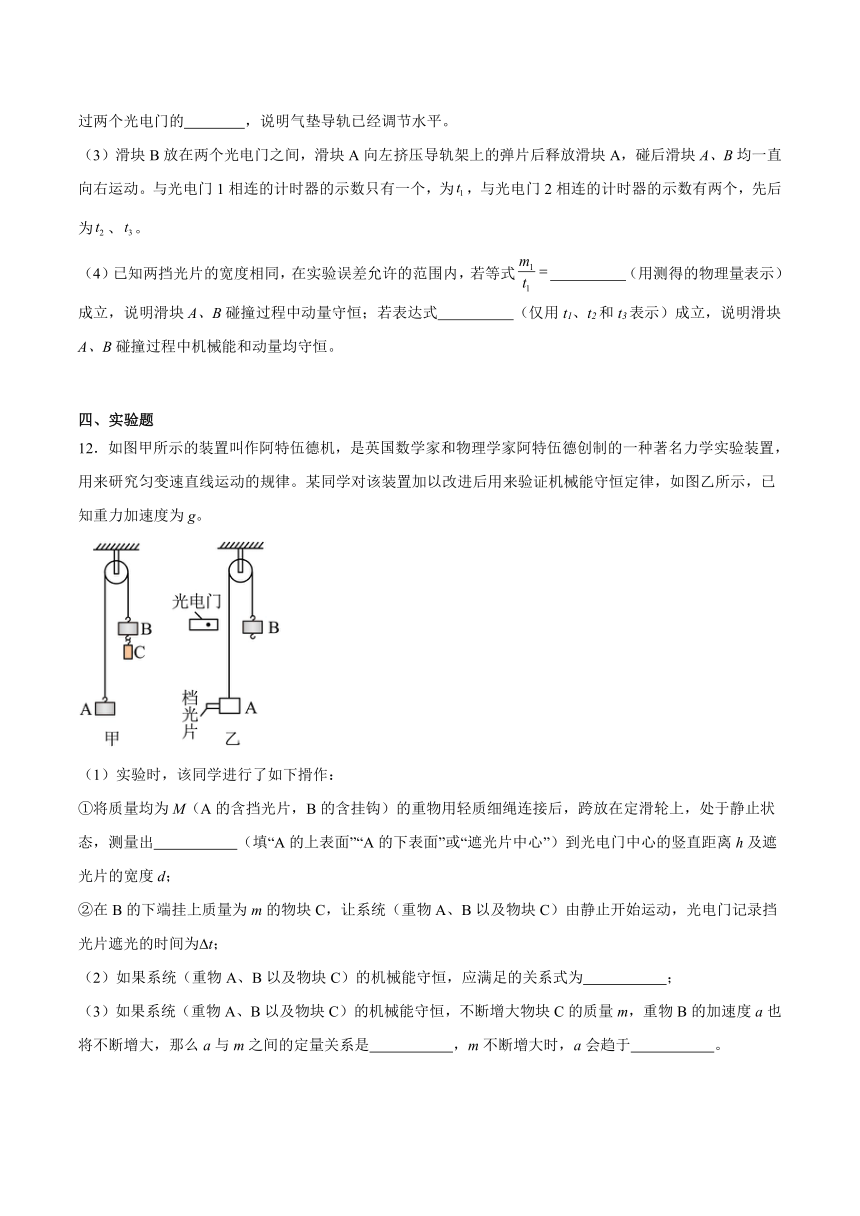
12.如图甲所示的装置叫作阿特伍德机,是英国数学家和物理学家阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律。某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示,已知重力加速度为g。
(1)实验时,该同学进行了如下搰作:
①将质量均为M(A的含挡光片,B的含挂钩)的重物用轻质细绳连接后,跨放在定滑轮上,处于静止状态,测量出 (填“A的上表面”“A的下表面”或“遮光片中心”)到光电门中心的竖直距离h及遮光片的宽度d;
②在B的下端挂上质量为m的物块C,让系统(重物A、B以及物块C)由静止开始运动,光电门记录挡光片遮光的时间为 t;
(2)如果系统(重物A、B以及物块C)的机械能守恒,应满足的关系式为 ;
(3)如果系统(重物A、B以及物块C)的机械能守恒,不断增大物块C的质量m,重物B的加速度a也将不断增大,那么a与m之间的定量关系是 ,m不断增大时,a会趋于 。
五、解答题
13.图甲是传统儿童玩具拨浪鼓,图乙是其结构示意图,在圆形鼓的直径两端系两根轻绳,轻绳下端连着两个相同的小球。鼓的半径为r,轻绳长度为r,小球的质量为m,重力加速度为g,当手柄竖直时,匀速转动手柄,轻绳与竖直方向的夹角为30°。不计空气阻力,求:
(1)轻绳对球的拉力大小。
(2)波浪鼓转动的角速度大小。
14.北京时间2024年7月31日,在巴黎奥运会自由式小轮车女子公园赛决赛中,中国选手邓雅文夺得金牌。这也是中国运动员第一次参加奥运会自由式小轮车项目。其部分场地可以简化为如图所示的模型,平台A左右弧面对称,右侧为半径的部分圆弧面,圆心角满足,平台B为的圆弧面,半径,邓雅文以一定的初速度从平台的左下端冲向平台A,从M点腾空后沿切线从N点进入赛道,再经过一段水平骑行从Q点进入平台B,恰好到达平台B的上端边缘,平台A上端MN间的距离为2.4m,邓雅文和独轮车总质量为75kg,运动过程中可视为质点,整个过程邓雅文只在PQ段进行了骑行做功,不计一切阻力,重力加速度取,求:
(1)邓雅文和独轮车到达Q点时赛道给独轮车的支持力大小;
(2)邓雅文和独轮车在MN段腾空最高处的速度;
(3)邓雅文在PQ段骑行过程中所做的功。
15.足够长的光滑水平面右侧有一固定的竖直挡板。物块A、B用一细线连接,二者之间压缩着一段轻弹簧(弹性限度内),弹簧与物块A拴接,但与物块B不栓接。烧断细线,物块A、B向两侧弹开,当弹簧恢复原长后,物块A、B将在水平面上分别向左、向右做匀速运动,直至物块B撞上右侧的竖直挡板被反弹,每次碰撞挡板后,物块B的动能都变为碰撞前的81%。物块A的质量为4kg,物块B的质量为1kg。弹簧第一次恢复原长时,物块A的速度为5m/s。物块B反弹后追上物块A时,挤压弹簧并再次被弹开。反复几次,直至不再追上物块A,求:
(1)烧断细线前,弹簧的弹性势能;
(2)物块B第一次被反弹后,追上物块A后弹簧弹性势能最大时,物块A的速度大小;
(3)物块B第二次被反弹后,试计算物块B能否追上物块A。
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C B B D B BD ABC AD
11. 调高 时间相等
【详解】(2)同一滑块通过两个光电门,由知,时间长的速度小,可知滑块做加速运动,导轨右端应调高一点,直至两个计时器显示的时间相等,即说明滑块做匀速直线运动,导轨已调成水平。
(4)滑块碰前速度,碰后速度,滑块碰后速度,在实验误差允许的范围内,若碰撞前后动量守恒,即,联立以上可得;若碰撞过程中机械能守恒,需满足,整理得,联立解得,故成立,说明滑块、碰撞过程中机械能和动量均守恒。
12. 遮光片中心
【详解】(1)①[1]实验时,因测量出的速度可视为挡光片中心的速度,所以测量出遮光片中心到光电门中心的竖直距离h。
(2)[2]重物A经过光电门时的速度为
如果系统(重物A、B以及物块C)的机械能守恒,应满足的关系式为
(3)[3][4]根据牛顿第二定律可知
解得a与m之间的定量关系是
当m增大时,式子的分母趋近于1,则a的值会趋于重力加速度g。
13.(1)
(2)
【详解】(1)对球进行受力分析,在竖直方向上
解得绳子的拉力
(2)在水平方向上,根据牛顿第二定律
可得波浪鼓转动的角速度
14.(1)2250N
(2)3m/s
(3)562.5J
【详解】(1)由于运动员恰好到达平台B的上端边缘,根据机械能守恒
根据牛顿第二定律
联立解得支持力大小
(2)运动员从M点做斜抛运动,设初速度为v,则
解得
因此在最高点的速度
(3)从M到Q的过程中,根据动能定理
解得
15.(1);(2);(3)不能,见解析
【详解】(1)烧断细线,物块A、B向两侧弹开,物块A、B动量守恒,则
解得
根据能量守恒,烧断细线前,弹簧的弹性势能
(2)物块B第一次被反弹后,物块B的动能都变为碰撞前的81%,则
解得
物块B第一次被反弹后,追上物块A后弹簧弹性势能最大时,物块A、B共速,根据动量守恒可得
解得物块A的速度大小为
(3)设物块A、B第二次被弹簧向两侧弹开时速度为、,根据动量守恒以及机械能守恒可得
解得
,
由于第二次被弹簧向两侧弹开时物块A的速度大小大于物块B的速度大小,物块B第二次被反弹后,物块B不能追上物块A。
一、单选题
1.关于运动和力,下列说法正确的是( )
A.物体受到的力不为恒力,物体一定做曲线运动
B.物体受到变化的合力作用时,它的速度大小一定改变
C.物体在不垂直于速度方向的合力作用下,速度大小可能一直不变
D.当物体受到与初速度方向不在同一条直线的合力作用时,物体一定做曲线运动
2.如图为直升飞机吊装全地形车的情景,飞机水平匀速飞行的同时把全地形车往上提升,让全地形车竖直向上做匀加速直线运动。若以全地形车刚开始向上运动的位置为坐标原点,竖直向上为y轴正方向,飞机飞行方向为x轴正方向,则全地形车的运动轨迹为( )
A.B.C. D.
3.我国北斗卫星导航系统(BDS)可以为全球提供定位、导航、授时、5G传输等服务。A、B为“北斗”系统中的两颗卫星,这两颗卫星均绕地球做匀速圆周运动。A、B两颗卫星在轨运行周期之比为k,则A、B两颗卫星与地心连线在单位时间内扫过的面积之比为( )
A.k B. C. D.
4.2024年第11号台风“摩羯”于9月6日在海南文昌登陆,登陆时中心附近最大风力有17级以上,造成具大破坏.已知11级台风的风速范围为,17级台风的风速范围为.若台风迎面垂直吹向一固定的交通标志牌,则17级台风对该标志牌的作用力大小约为11级台风的( )
A.2倍 B.4倍 C.8倍 D.16倍
5.如图所示,楔形木块固定在水平面上,光滑斜面与水平面的夹角为60°,粗糙斜面与水平面的夹角为30°,与均足够长。长为l、质量为m、粗细均匀、质量分布均匀的软绳放置于上,其上端与B齐平。质量为2m的物块通过一根不计质量的细线与软绳上端相连,并放置于上,物块由静止释放后沿下滑(重力加速度为g),直到软绳刚好离开完全进入,在此过程中( )
A.物块和软绳组成的系统机械能守恒
B.软绳的重力势能减少
C.物块的重力势能减少
D.软绳克服摩擦力做的功等于软绳的机械能减少量
6.2024年9月24日,我国全球首个医学遥感卫星(珞珈四号01星)成功发射,卫星在离地面约的高度绕地球做匀速圆周运动;2022年4月15日,我国新一代地球同步轨道通信卫星(中星卫星)成功发射,卫星在离地面约的高度绕地球做匀速圆周运动;地球赤道上有一物体。关于赤道上物体、珞珈四号01星、中星卫星,下列说法正确的是( )
A.赤道上物体的线速度最大
B.赤道上物体的周期小于中星卫星的周期
C.珞珈四号01星的角速度小于中星6D卫星的角速度
D.珞珈四号01星的向心加速度大于中星卫星的向心加速度
7.如图所示,光滑水平面上甲、乙两球间粘少许炸药,一起以速度0.5 m/s向右做匀速直线运动。已知甲、乙两球质量分别为0.1 kg和0.2 kg。某时刻炸药突然爆炸,分开后两球仍沿原直线运动,从爆炸开始计时经过3.0 s,两球之间的距离为x = 2.7 m,则说法正确的是( )
A.刚分离时,甲、乙两球的速度方向相同
B.刚分离时,甲球的速度大小为0.1 m/s,方向水平向左
C.刚分离时,乙球的速度大小为0.3 m/s
D.爆炸过程中释放的能量为0.27 J
二、多选题
8.水车是中国最古老的农业灌溉工具,是珍贵的历史文化遗产。水车的简易模型如图所示,水流自水平放置的水管流出,水流轨迹与水车车轮的边缘相切,可使车轮持续转动,切点与所在车轮横截面的圆心的连线与水平方向的夹角为。若水管出水口处水流的速度大小为,车轮半径,不计空气阻力,重力加速度大小取0.8,水流到达车轮边缘时的速度与车轮边缘切点的线速度相同,则下列说法正确的是( )
A.水管出水口距轮轴的水平距离为
B.水管出水口距轮轴的竖直距离为
C.车轮的角速度是
D.从出水口到车轮边缘的过程中,水流速度变化量的大小为
9.我国首次火星探测任务已取得圆满成功。着陆器着陆前的模拟轨迹如图所示,先在轨道I上运动,经过点启动变轨发动机切换到圆轨道II上运动,经过一段时间后,再次经过点时启动变轨发动机切换到圆轨道III上运动。轨道上的三点与火星中心位于同一直线上,两点分别是椭圆轨道的远火星点和近火星点,且(R为火星的半径)。着陆器在轨道I、Ⅱ、III上经过点的速度分别为,在轨道Ⅱ上的运行周期为,引力常量为,下列说法正确的是( )
A.
B.火星的密度为
C.着陆器变轨前在轨道I上运动时,经过点的加速度为
D.着陆器在轨道Ⅱ上经过点的机械能小于轨道III上经过点的机械能
10.中国目前拥有世界上最完善的高铁系统,高铁是中国科技发展的一张世界名片。假设有一动车组由四节车厢连接而成,每节车厢的质量均为、阻力均恒为,其中第一节和第四节为动力车厢,功率均恒为P,重力加速度为g。该动车组由静止开始恒定功率启动,下列说法正确的是( )
A.该动车组的最大行驶速度为
B.由静止到最大速度过程的平均速度为
C.该动车组速度达到最大时,第二、三两节车厢之间的作用力大小为
D.当速度为最大值的一半时,动车组运行的加速度大小为
11.某学习小组采用如图所示的装置验证滑块碰撞过程中的动量守恒。
(1)用天平测得滑块A、B(均包括挡光片)的质量分别为、。
(2)接通充气泵电源后,导轨左侧放一滑块并推动滑块,滑块通过两个光电门时,与光电门1、2相连的计时器测得的挡光时间分别为0.07s、0.06s,则应将导轨右端 (选填“调高”或“调低”),直至滑块通过两个光电门的 ,说明气垫导轨已经调节水平。
(3)滑块B放在两个光电门之间,滑块A向左挤压导轨架上的弹片后释放滑块A,碰后滑块A、B均一直向右运动。与光电门1相连的计时器的示数只有一个,为,与光电门2相连的计时器的示数有两个,先后为、。
(4)已知两挡光片的宽度相同,在实验误差允许的范围内,若等式 (用测得的物理量表示)成立,说明滑块A、B碰撞过程中动量守恒;若表达式 (仅用t1、t2和t3表示)成立,说明滑块A、B碰撞过程中机械能和动量均守恒。
四、实验题
12.如图甲所示的装置叫作阿特伍德机,是英国数学家和物理学家阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律。某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示,已知重力加速度为g。
(1)实验时,该同学进行了如下搰作:
①将质量均为M(A的含挡光片,B的含挂钩)的重物用轻质细绳连接后,跨放在定滑轮上,处于静止状态,测量出 (填“A的上表面”“A的下表面”或“遮光片中心”)到光电门中心的竖直距离h及遮光片的宽度d;
②在B的下端挂上质量为m的物块C,让系统(重物A、B以及物块C)由静止开始运动,光电门记录挡光片遮光的时间为 t;
(2)如果系统(重物A、B以及物块C)的机械能守恒,应满足的关系式为 ;
(3)如果系统(重物A、B以及物块C)的机械能守恒,不断增大物块C的质量m,重物B的加速度a也将不断增大,那么a与m之间的定量关系是 ,m不断增大时,a会趋于 。
五、解答题
13.图甲是传统儿童玩具拨浪鼓,图乙是其结构示意图,在圆形鼓的直径两端系两根轻绳,轻绳下端连着两个相同的小球。鼓的半径为r,轻绳长度为r,小球的质量为m,重力加速度为g,当手柄竖直时,匀速转动手柄,轻绳与竖直方向的夹角为30°。不计空气阻力,求:
(1)轻绳对球的拉力大小。
(2)波浪鼓转动的角速度大小。
14.北京时间2024年7月31日,在巴黎奥运会自由式小轮车女子公园赛决赛中,中国选手邓雅文夺得金牌。这也是中国运动员第一次参加奥运会自由式小轮车项目。其部分场地可以简化为如图所示的模型,平台A左右弧面对称,右侧为半径的部分圆弧面,圆心角满足,平台B为的圆弧面,半径,邓雅文以一定的初速度从平台的左下端冲向平台A,从M点腾空后沿切线从N点进入赛道,再经过一段水平骑行从Q点进入平台B,恰好到达平台B的上端边缘,平台A上端MN间的距离为2.4m,邓雅文和独轮车总质量为75kg,运动过程中可视为质点,整个过程邓雅文只在PQ段进行了骑行做功,不计一切阻力,重力加速度取,求:
(1)邓雅文和独轮车到达Q点时赛道给独轮车的支持力大小;
(2)邓雅文和独轮车在MN段腾空最高处的速度;
(3)邓雅文在PQ段骑行过程中所做的功。
15.足够长的光滑水平面右侧有一固定的竖直挡板。物块A、B用一细线连接,二者之间压缩着一段轻弹簧(弹性限度内),弹簧与物块A拴接,但与物块B不栓接。烧断细线,物块A、B向两侧弹开,当弹簧恢复原长后,物块A、B将在水平面上分别向左、向右做匀速运动,直至物块B撞上右侧的竖直挡板被反弹,每次碰撞挡板后,物块B的动能都变为碰撞前的81%。物块A的质量为4kg,物块B的质量为1kg。弹簧第一次恢复原长时,物块A的速度为5m/s。物块B反弹后追上物块A时,挤压弹簧并再次被弹开。反复几次,直至不再追上物块A,求:
(1)烧断细线前,弹簧的弹性势能;
(2)物块B第一次被反弹后,追上物块A后弹簧弹性势能最大时,物块A的速度大小;
(3)物块B第二次被反弹后,试计算物块B能否追上物块A。
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C B B D B BD ABC AD
11. 调高 时间相等
【详解】(2)同一滑块通过两个光电门,由知,时间长的速度小,可知滑块做加速运动,导轨右端应调高一点,直至两个计时器显示的时间相等,即说明滑块做匀速直线运动,导轨已调成水平。
(4)滑块碰前速度,碰后速度,滑块碰后速度,在实验误差允许的范围内,若碰撞前后动量守恒,即,联立以上可得;若碰撞过程中机械能守恒,需满足,整理得,联立解得,故成立,说明滑块、碰撞过程中机械能和动量均守恒。
12. 遮光片中心
【详解】(1)①[1]实验时,因测量出的速度可视为挡光片中心的速度,所以测量出遮光片中心到光电门中心的竖直距离h。
(2)[2]重物A经过光电门时的速度为
如果系统(重物A、B以及物块C)的机械能守恒,应满足的关系式为
(3)[3][4]根据牛顿第二定律可知
解得a与m之间的定量关系是
当m增大时,式子的分母趋近于1,则a的值会趋于重力加速度g。
13.(1)
(2)
【详解】(1)对球进行受力分析,在竖直方向上
解得绳子的拉力
(2)在水平方向上,根据牛顿第二定律
可得波浪鼓转动的角速度
14.(1)2250N
(2)3m/s
(3)562.5J
【详解】(1)由于运动员恰好到达平台B的上端边缘,根据机械能守恒
根据牛顿第二定律
联立解得支持力大小
(2)运动员从M点做斜抛运动,设初速度为v,则
解得
因此在最高点的速度
(3)从M到Q的过程中,根据动能定理
解得
15.(1);(2);(3)不能,见解析
【详解】(1)烧断细线,物块A、B向两侧弹开,物块A、B动量守恒,则
解得
根据能量守恒,烧断细线前,弹簧的弹性势能
(2)物块B第一次被反弹后,物块B的动能都变为碰撞前的81%,则
解得
物块B第一次被反弹后,追上物块A后弹簧弹性势能最大时,物块A、B共速,根据动量守恒可得
解得物块A的速度大小为
(3)设物块A、B第二次被弹簧向两侧弹开时速度为、,根据动量守恒以及机械能守恒可得
解得
,
由于第二次被弹簧向两侧弹开时物块A的速度大小大于物块B的速度大小,物块B第二次被反弹后,物块B不能追上物块A。
同课章节目录
