6.1.2 向量的加法(教学课件)__高中数学人教B版(2019)必修第二册(共25张PPT)
文档属性
| 名称 | 6.1.2 向量的加法(教学课件)__高中数学人教B版(2019)必修第二册(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 30.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 05:22:06 | ||
图片预览






文档简介
(共25张PPT)
6.1.2 向量的加法
人教B版(2019)必修第一册
第六章 平面向量初步
学习目标
掌握向量的加法运算
01
理解向量加法的三角形法则和平行四边形
02
理解向量的加法交换律和结合律
03
情境与问题
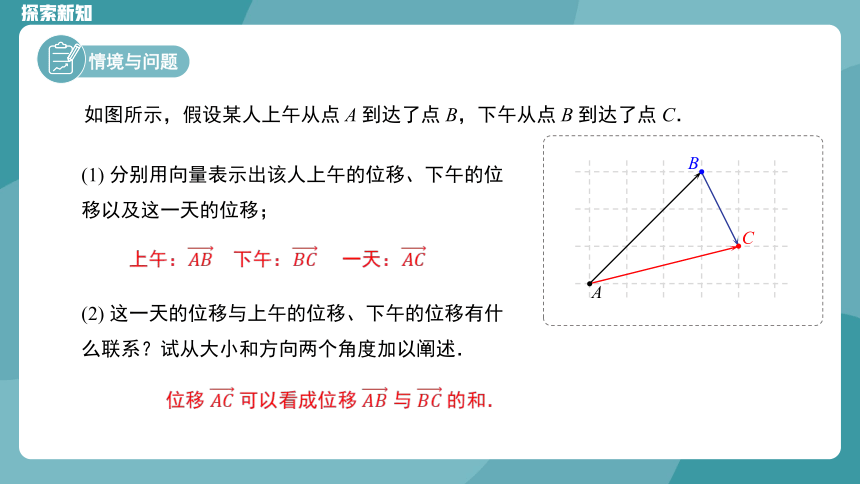
如图所示,假设某人上午从点 A 到达了点 B,下午从点 B 到达了点 C.
探索新知
(1) 分别用向量表示出该人上午的位移、下午的位移以及这一天的位移;
(2) 这一天的位移与上午的位移、下午的位移有什么联系?试从大小和方向两个角度加以阐述.
A
B
C
上午:
下午:
一天:
位移 可以看成位移 与 的和.
探索新知
向量加法的三角形法则
向量的和:一般地,平面上任意给定两个向量 a,b,在该平面内任取一点A,作 =a, =b,作出向量 ,则向量 称为向量 (也称 为向量 a 与 b 的和向量).
a 与 b 的和
a+b
向量 a 与 b 的和向量记作 ,因此
探索新知
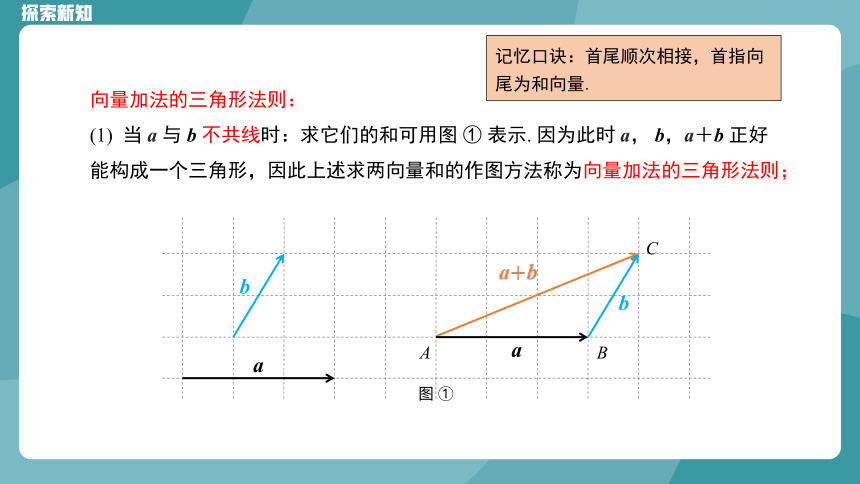
向量加法的三角形法则:
(1) 当 a 与 b 不共线时:求它们的和可用图 ① 表示. 因为此时 a, b,a+b 正好能构成一个三角形,因此上述求两向量和的作图方法称为向量加法的三角形法则;
a
b
a
b
ab
图 ①
A
B
C
记忆口诀:首尾顺次相接,首指向尾为和向量.
探索新知
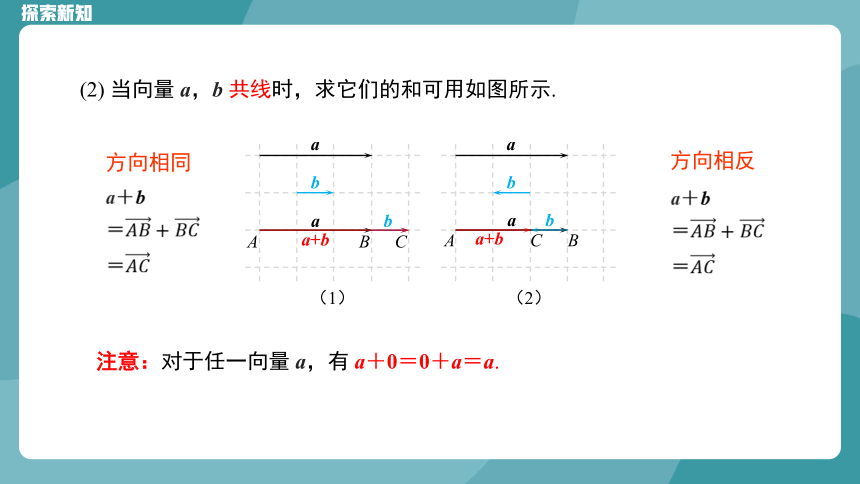
(2) 当向量 a,b 共线时,求它们的和可用如图所示.
A
B
C
a
b
a+b
b
a
a+b
b
a
A
B
C
a
b
(1)
(2)
方向相同
方向相反
a+b
=
=
a+b
=
=
注意:对于任一向量 a,有 a+0=0+a=a.
探索新知
向量和的三角表示
(1) 因为三角形中两边之和大于第三边,两边之差小于第三边,由向量加法的三角形法则知,当 不共线时,恒有 |
(2) 当 同向共线时, 同向,
综上,有向量和的三角不等式 .
(3) 当 反向共线时,
若 则 与 同向,
若 则 与 同向,
典型例题
例 1 已知 |a|=3,|b|=4,求 | a+b | 的最大值和最小值,并说明取得最大值和最小值时 a 与 b 的关系.
解:由 | a+b |≤|a|+|b| 可知,| a+b |的最大值为
|a|+|b|=3 4 =7,
当且仅当 a 与 b 方向相同时取得最大值.
由 | a+b |≥| |a|-|b| | 可知,| a+b | 的最小值为
| |a|-|b| |=4-3=1,
当且仅当 a 与 b 方向相反时取得最小值.
情境与问题
从物理学中我们已经知道,力既有大小也有方向,因此力是向量.
探索新知
A
B
C
当在光滑的水平面上沿两个不同的方向拉动一个静止的物体时,如图所示,物体会沿着力 或 所在的方向运动吗?如果不会,物体的运动方向将是怎样的?
我们知道,物理学中力的合成遵循平行四边形法则. 因此,情境中的物体不会沿着 或 所在的方向运动;其会沿着以 AB,AC 为邻边的平行四边形的对角线运动.
探索新知
如图所示,平面上任意给定两个不共线的向量 a,b,在该平面内任取一点 A,作 =a,=b,以 AB、AC 为邻边作一个平行四边形 ABDC,作出向量 ,因为 = ,所以 = + = + .
a
b
a
ab
b
A
B
C
D
一般地,向量的加法也满足类似的法则,这就是说,当两个向量不共线时,可以通过作平行四边形的方法来得到它们的和:
这种求两向量和的作图方法称为向量加法的平行四边形法则.
探索新知
思考:数的加法满足交换律,向量的加法是否也满足交换律呢?
满足交换律
A
O
B
C
探索新知
从前面已经知道,两个向量的和还是一个向量,因此我们可以用得到和向量与另外一个向量相加.而且我们也已经知道,如同数与数的加法一样,向量相加满足交换律,那么向量相加是否满足结合律呢?也就是说,三个向量相加时,最后的结果是否与求和的顺序有关呢?
满足结合律.
三个向量相加时,最后的结果与求和的顺序无关.因为向量的加法运算满足交换律和结合律,所以有限个向量相加的结果是唯一的,我们可以任意调换其中向量的位置,也可以任意决定相加的顺序.
探索新知
如图所示,(1) 中给出了三个向量 a、b、c;(2) 中先作出了向量 a+b,然后作出了向量 (a+b)+c;(3) 中首先作出了向量 b+c,然后作出了向量 a+(b+c).
a
a
b
b
c
c
a+b
b+c
(a+b)+c
a+(b+c)
(2)
(3)
a
b
c
(1)
不难看出, (a+b)+c=a+(b+c)
即向量的加法运算满足结合律.
探索新知
因为向量的加法运算满足交换律和结合律,所以有限个向量相加的结果是唯一的,我们可以任意调换其中向量的位置,也可以任意决定相加的顺序.例如
(a+b)+(c+b)=a+[(b+c)+d]
=[(d+c)+a]+b
因此,以上运算我们都可用 a+b+c+b 表示.
探索新知
为了得到有限个向量的和,只需将这些向量依次首尾相接,那么以第一个向量的始点为始点,最后一个向量的终点为终点的向量,就是这些向量的和,如下所示.
a
b
c
d
e
a+b+c+d+e
a
b
e
c
d
问题 图中向量的和,与向量相加的顺序有关吗?为什么?
无关.
原因在于向量的加法运算满足交换律,因此可以任意调整有关顺序.事实上,由于向量的加法满足交换律和结合律,所以有限个向量相加的结果是唯一的.
典型例题
例 2 化简下列各式:
(1) + + ;(2) + + + + .
解:(1) + + = (+ ) + + ;
+ + + + = + +( + + )
= + +
= (+ ) +
= +
= = 0.
探索新知
探索与研究
在求作两个向量的和时,可以选择不同的始点. 想一想,选择不同的始点作出的向量和都相等吗?你可能认识,作出的向量和显然都是相等的. 当然,这里你的“显然”是对的,你能根据右图说明这个结论的正确性吗?
如图所示,∵ ,∴ 四边形 为平行四边形,
∴ AA′ BB′,同理 BB′ CC′,∴ AA′ CC′,
∴ 四边形 AA′C′C 为平行四边形,∴ AC A′C′.
又 与 方向相同,∴ =,即结论成立.
当堂检测
当堂检测
C
当堂检测
ABCD
当堂检测
C
当堂检测
km
当堂检测
本节课学习了哪些知识点呢?
1. 向量加法的三角形法则;
2. 向量加法的平行四边形法则;
3. 向量的交换律、结合律.
感谢观看
祝同学新学期新气象
6.1.2 向量的加法
人教B版(2019)必修第一册
第六章 平面向量初步
学习目标
掌握向量的加法运算
01
理解向量加法的三角形法则和平行四边形
02
理解向量的加法交换律和结合律
03
情境与问题
如图所示,假设某人上午从点 A 到达了点 B,下午从点 B 到达了点 C.
探索新知
(1) 分别用向量表示出该人上午的位移、下午的位移以及这一天的位移;
(2) 这一天的位移与上午的位移、下午的位移有什么联系?试从大小和方向两个角度加以阐述.
A
B
C
上午:
下午:
一天:
位移 可以看成位移 与 的和.
探索新知
向量加法的三角形法则
向量的和:一般地,平面上任意给定两个向量 a,b,在该平面内任取一点A,作 =a, =b,作出向量 ,则向量 称为向量 (也称 为向量 a 与 b 的和向量).
a 与 b 的和
a+b
向量 a 与 b 的和向量记作 ,因此
探索新知
向量加法的三角形法则:
(1) 当 a 与 b 不共线时:求它们的和可用图 ① 表示. 因为此时 a, b,a+b 正好能构成一个三角形,因此上述求两向量和的作图方法称为向量加法的三角形法则;
a
b
a
b
ab
图 ①
A
B
C
记忆口诀:首尾顺次相接,首指向尾为和向量.
探索新知
(2) 当向量 a,b 共线时,求它们的和可用如图所示.
A
B
C
a
b
a+b
b
a
a+b
b
a
A
B
C
a
b
(1)
(2)
方向相同
方向相反
a+b
=
=
a+b
=
=
注意:对于任一向量 a,有 a+0=0+a=a.
探索新知
向量和的三角表示
(1) 因为三角形中两边之和大于第三边,两边之差小于第三边,由向量加法的三角形法则知,当 不共线时,恒有 |
(2) 当 同向共线时, 同向,
综上,有向量和的三角不等式 .
(3) 当 反向共线时,
若 则 与 同向,
若 则 与 同向,
典型例题
例 1 已知 |a|=3,|b|=4,求 | a+b | 的最大值和最小值,并说明取得最大值和最小值时 a 与 b 的关系.
解:由 | a+b |≤|a|+|b| 可知,| a+b |的最大值为
|a|+|b|=3 4 =7,
当且仅当 a 与 b 方向相同时取得最大值.
由 | a+b |≥| |a|-|b| | 可知,| a+b | 的最小值为
| |a|-|b| |=4-3=1,
当且仅当 a 与 b 方向相反时取得最小值.
情境与问题
从物理学中我们已经知道,力既有大小也有方向,因此力是向量.
探索新知
A
B
C
当在光滑的水平面上沿两个不同的方向拉动一个静止的物体时,如图所示,物体会沿着力 或 所在的方向运动吗?如果不会,物体的运动方向将是怎样的?
我们知道,物理学中力的合成遵循平行四边形法则. 因此,情境中的物体不会沿着 或 所在的方向运动;其会沿着以 AB,AC 为邻边的平行四边形的对角线运动.
探索新知
如图所示,平面上任意给定两个不共线的向量 a,b,在该平面内任取一点 A,作 =a,=b,以 AB、AC 为邻边作一个平行四边形 ABDC,作出向量 ,因为 = ,所以 = + = + .
a
b
a
ab
b
A
B
C
D
一般地,向量的加法也满足类似的法则,这就是说,当两个向量不共线时,可以通过作平行四边形的方法来得到它们的和:
这种求两向量和的作图方法称为向量加法的平行四边形法则.
探索新知
思考:数的加法满足交换律,向量的加法是否也满足交换律呢?
满足交换律
A
O
B
C
探索新知
从前面已经知道,两个向量的和还是一个向量,因此我们可以用得到和向量与另外一个向量相加.而且我们也已经知道,如同数与数的加法一样,向量相加满足交换律,那么向量相加是否满足结合律呢?也就是说,三个向量相加时,最后的结果是否与求和的顺序有关呢?
满足结合律.
三个向量相加时,最后的结果与求和的顺序无关.因为向量的加法运算满足交换律和结合律,所以有限个向量相加的结果是唯一的,我们可以任意调换其中向量的位置,也可以任意决定相加的顺序.
探索新知
如图所示,(1) 中给出了三个向量 a、b、c;(2) 中先作出了向量 a+b,然后作出了向量 (a+b)+c;(3) 中首先作出了向量 b+c,然后作出了向量 a+(b+c).
a
a
b
b
c
c
a+b
b+c
(a+b)+c
a+(b+c)
(2)
(3)
a
b
c
(1)
不难看出, (a+b)+c=a+(b+c)
即向量的加法运算满足结合律.
探索新知
因为向量的加法运算满足交换律和结合律,所以有限个向量相加的结果是唯一的,我们可以任意调换其中向量的位置,也可以任意决定相加的顺序.例如
(a+b)+(c+b)=a+[(b+c)+d]
=[(d+c)+a]+b
因此,以上运算我们都可用 a+b+c+b 表示.
探索新知
为了得到有限个向量的和,只需将这些向量依次首尾相接,那么以第一个向量的始点为始点,最后一个向量的终点为终点的向量,就是这些向量的和,如下所示.
a
b
c
d
e
a+b+c+d+e
a
b
e
c
d
问题 图中向量的和,与向量相加的顺序有关吗?为什么?
无关.
原因在于向量的加法运算满足交换律,因此可以任意调整有关顺序.事实上,由于向量的加法满足交换律和结合律,所以有限个向量相加的结果是唯一的.
典型例题
例 2 化简下列各式:
(1) + + ;(2) + + + + .
解:(1) + + = (+ ) + + ;
+ + + + = + +( + + )
= + +
= (+ ) +
= +
= = 0.
探索新知
探索与研究
在求作两个向量的和时,可以选择不同的始点. 想一想,选择不同的始点作出的向量和都相等吗?你可能认识,作出的向量和显然都是相等的. 当然,这里你的“显然”是对的,你能根据右图说明这个结论的正确性吗?
如图所示,∵ ,∴ 四边形 为平行四边形,
∴ AA′ BB′,同理 BB′ CC′,∴ AA′ CC′,
∴ 四边形 AA′C′C 为平行四边形,∴ AC A′C′.
又 与 方向相同,∴ =,即结论成立.
当堂检测
当堂检测
C
当堂检测
ABCD
当堂检测
C
当堂检测
km
当堂检测
本节课学习了哪些知识点呢?
1. 向量加法的三角形法则;
2. 向量加法的平行四边形法则;
3. 向量的交换律、结合律.
感谢观看
祝同学新学期新气象
