6.1.1 向量的概念(教学课件)__高中数学人教B版(2019)必修第二册(共27张PPT)
文档属性
| 名称 | 6.1.1 向量的概念(教学课件)__高中数学人教B版(2019)必修第二册(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 41.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 05:22:51 | ||
图片预览






文档简介
(共27张PPT)
6.1.1 向量的概念
人教B版(2019)必修第一册
第六章 平面向量初步
学习目标
了解向量的概念及实际背景
01
了解零向量、单位向量、向量的模等概念
02
理解相等向量
03
理解共线向量(平行向量)、位置向量
04
情境与问题
我们在物理学中已经学过位移的有关知识,知道位移是表示物体位置变化的物理量. 如图所示,当物体从 A 运动到 B 时,不管沿着什么轨迹,它的位移都是一样的,即 “向北 300 m”.
探索新知
100 m
A
B
C
D
北
(1) 图中,从 B 到 A 的位移是“__________________”,
它与从 A 到 B 的位移有什么关系?
(2) 怎样直观地表示位移?用你的方法表示出图中从 A 到 B,从 A 到 C,从 A 到 D 的位移,说出这三个位移之间的关系.
向南 300 m
二者方向相反
AB,与 AC、AD 的位移方向不同,AC 的位移与 AD 的位移方向相同
探索新知
位移与向量
向量:既有 又有 的量称为向量 (也称为矢量).
位移被“方向”和“距离”唯一确定,其中“距离”也称为位移的大小.
向量与标量的区别
向量有方向,而标量没有方向;标量与标量之间可以比较大小,而向量与向量之间不能比较大小.
大小
方向
模:向量的大小也称为向量的模 (或长度);只有大小的量称为标量,长度、面积等都是标量.
探索新知
位移与向量
向量的表示:用 来直观地表示向量.
通常将有向线段不带箭头的端点称为向量的始点 (或起点),带箭头的端点称为向量的 . 有向线段始点和终点的相对位置确定向量的大小与方向. 始点为 A 终点为 B 的有向线段表示的向量,可以用符号简记为 ,此时向量的大小用 表示.
我们知道,位移可以用带箭头的线段 (即有向线段) 来直观地表示.
有向线段
向量的大小:有向线段的 表示向量的大小.
长度
向量的方向:有向线段箭头所指的方向表示向量的方向.
终点
.
探索新知
A
B
C
D
E
F
G
H
a
b
c
d
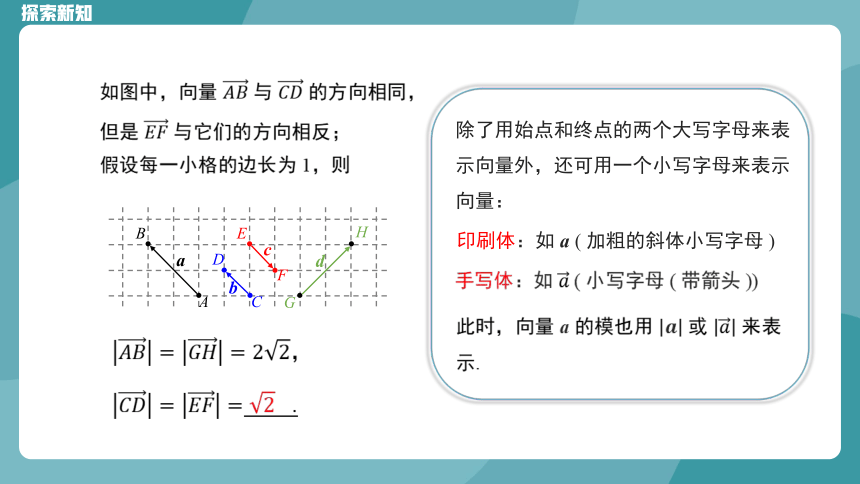
如图中,向量 与 的方向相同,
但是 与它们的方向相反;
假设每一小格的边长为 1,则
,
除了用始点和终点的两个大写字母来表示向量外,还可用一个小写字母来表示向量:
印刷体:如 a ( 加粗的斜体小写字母 )
手写体:如 ( 小写字母 ( 带箭头 ))
此时,向量 a 的模也用 或 来表示.
探索新知
零向量与单位向量
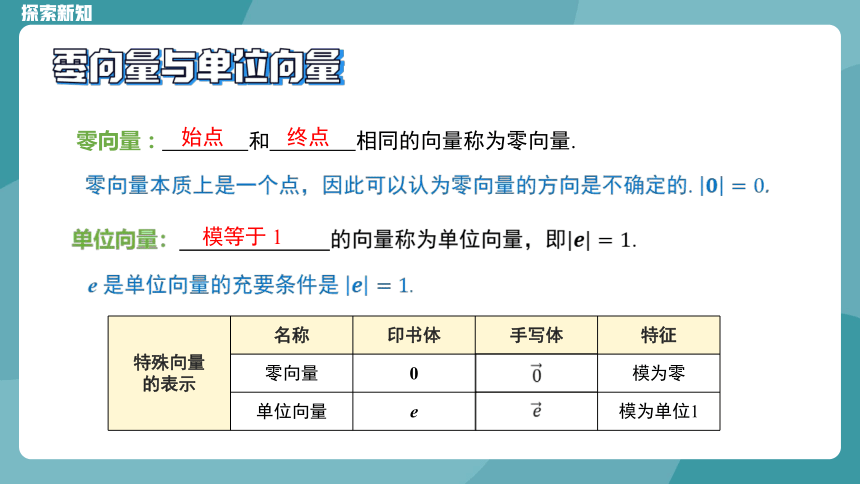
零向量: 和 相同的向量称为零向量.
单位向量: 的向量称为单位向量,即.
始点
终点
零向量本质上是一个点,因此可以认为零向量的方向是不确定的. .
模等于 1
特殊向量 的表示 名称 印书体 手写体 特征
零向量 0 模为零
单位向量 e 模为单位1
e 是单位向量的充要条件是 .
探索新知
零向量与单位向量
对0、单位向量的理解:
(1) 若用有向线段表示零向量,则其终点与始点重合,其本质是一个点. 零向量的方向不确定,不能说零向量没有方向.
(2) 要注意 0 与 0 的区别与联系:0 是一个实数,0 是一个向量,且有 |0|=0;书写时表示零向量,一定不能漏掉 0 上的箭头.
(3)单位向量有无数个,它们大小相等,但方向不一定相同.
典型例题
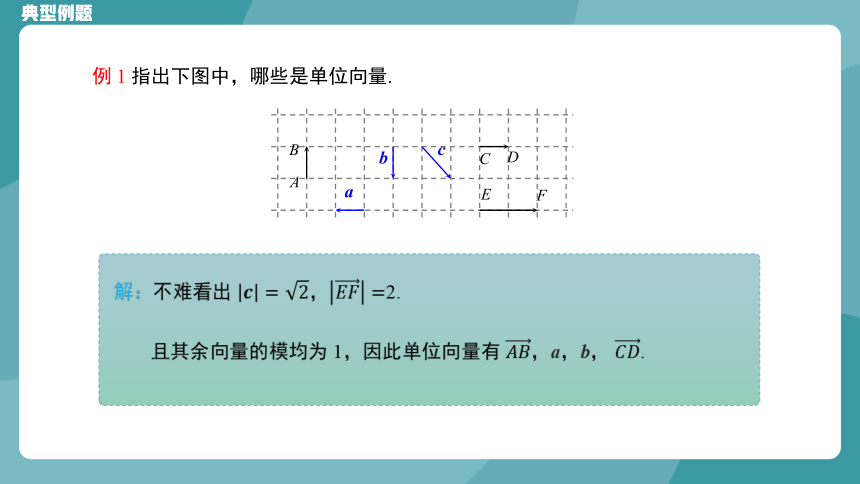
例 1 指出下图中,哪些是单位向量.
解:不难看出 ,2.
且其余向量的模均为 1,因此单位向量有 ,a,b, .
a
b
c
A
B
C
D
E
F
情境与问题
上体育课时,当某一排同学整理好队形,并执行完老师的口令 “向前三步走,向右看齐” 之后,同学们位移的方向是否相同?位移的大小是否相等?能否认为同学们的位移是相同的?
探索新知
可以认为,情境中同学们位移的方向和大小都相等,即位移相同.
相等向量: 的向量称为相等的向量.
大小相等、方向相同
向量 a 和 b 相等,记作:a=b .
探索新知
尝试与发现
下图中,相等的向量有
a=, .
a
b
B
A
D
C
d
c
F
E
典型例题
例 2 如图,已知四边形 ABCD,则“”
是“四边形 ABCD 为平行四边形”的什么条件?
解:如果 ,那就表示这两个向量的方向相同且大小相等;
由图可知 ABDC 且 AB∥DC,因此四边形 ABCD 为平行四边形.
反之,如果四边形 ABCD 为平行四边形,
则 ABDC 且 AB∥DC,则 .
综上,“”是“四边形 ABCD 为平行四边形”的充要条件.
典型例题
例 3 如图所示,O 是正六边形 ABCDEF 的中心,以图中字母为始点或终点,分别写出与向量 ,, 相等的向量.
解:因为两个向量相等,只要方向相同大小相等即可,因此
A
B
C
D
E
F
O
探索新知
共线向量
向量的平行:如果两个非零向量的方向 ,则称这两个向量平行,两个向量平行也称两个向量共线 .
对向量平行的理解
(1) 向量平行 (共线) 时,表示向量的有向线段所在的直线平行或重合.
(2) 向量共线中的“共线”的含义不是平面几何中的“共线”的含义.共线向量有四种情况:方向相同模相等;方向相同模不等;方向相反模相等;方向相反模不等.
(3) 任一向量 a 都与它本身平行.
相同或者相反
平行
规定:零向量与任意向量 .
记作:a ∥b .
典型例题
例 4 如图所示,找出其中共线的向量,并写出共线向量模之间的关系
解:不难看出
a
b
d
e
f
c
a∥c 且
b∥d 且
e∥f 且
当堂检测
当堂检测
B
当堂检测
D
当堂检测
BD
当堂检测
D
当堂检测
D
当堂检测
B
当堂检测
当堂检测
A
当堂检测
D
本节课学习了哪些知识点呢?
1. 向量的定义:方向、大小;
2. 向量的表示;
3. 特殊向量:单位向量、零向量;
4. 特殊关系:相等向量、共线向量.
感谢观看
祝同学新学期新气象
6.1.1 向量的概念
人教B版(2019)必修第一册
第六章 平面向量初步
学习目标
了解向量的概念及实际背景
01
了解零向量、单位向量、向量的模等概念
02
理解相等向量
03
理解共线向量(平行向量)、位置向量
04
情境与问题
我们在物理学中已经学过位移的有关知识,知道位移是表示物体位置变化的物理量. 如图所示,当物体从 A 运动到 B 时,不管沿着什么轨迹,它的位移都是一样的,即 “向北 300 m”.
探索新知
100 m
A
B
C
D
北
(1) 图中,从 B 到 A 的位移是“__________________”,
它与从 A 到 B 的位移有什么关系?
(2) 怎样直观地表示位移?用你的方法表示出图中从 A 到 B,从 A 到 C,从 A 到 D 的位移,说出这三个位移之间的关系.
向南 300 m
二者方向相反
AB,与 AC、AD 的位移方向不同,AC 的位移与 AD 的位移方向相同
探索新知
位移与向量
向量:既有 又有 的量称为向量 (也称为矢量).
位移被“方向”和“距离”唯一确定,其中“距离”也称为位移的大小.
向量与标量的区别
向量有方向,而标量没有方向;标量与标量之间可以比较大小,而向量与向量之间不能比较大小.
大小
方向
模:向量的大小也称为向量的模 (或长度);只有大小的量称为标量,长度、面积等都是标量.
探索新知
位移与向量
向量的表示:用 来直观地表示向量.
通常将有向线段不带箭头的端点称为向量的始点 (或起点),带箭头的端点称为向量的 . 有向线段始点和终点的相对位置确定向量的大小与方向. 始点为 A 终点为 B 的有向线段表示的向量,可以用符号简记为 ,此时向量的大小用 表示.
我们知道,位移可以用带箭头的线段 (即有向线段) 来直观地表示.
有向线段
向量的大小:有向线段的 表示向量的大小.
长度
向量的方向:有向线段箭头所指的方向表示向量的方向.
终点
.
探索新知
A
B
C
D
E
F
G
H
a
b
c
d
如图中,向量 与 的方向相同,
但是 与它们的方向相反;
假设每一小格的边长为 1,则
,
除了用始点和终点的两个大写字母来表示向量外,还可用一个小写字母来表示向量:
印刷体:如 a ( 加粗的斜体小写字母 )
手写体:如 ( 小写字母 ( 带箭头 ))
此时,向量 a 的模也用 或 来表示.
探索新知
零向量与单位向量
零向量: 和 相同的向量称为零向量.
单位向量: 的向量称为单位向量,即.
始点
终点
零向量本质上是一个点,因此可以认为零向量的方向是不确定的. .
模等于 1
特殊向量 的表示 名称 印书体 手写体 特征
零向量 0 模为零
单位向量 e 模为单位1
e 是单位向量的充要条件是 .
探索新知
零向量与单位向量
对0、单位向量的理解:
(1) 若用有向线段表示零向量,则其终点与始点重合,其本质是一个点. 零向量的方向不确定,不能说零向量没有方向.
(2) 要注意 0 与 0 的区别与联系:0 是一个实数,0 是一个向量,且有 |0|=0;书写时表示零向量,一定不能漏掉 0 上的箭头.
(3)单位向量有无数个,它们大小相等,但方向不一定相同.
典型例题
例 1 指出下图中,哪些是单位向量.
解:不难看出 ,2.
且其余向量的模均为 1,因此单位向量有 ,a,b, .
a
b
c
A
B
C
D
E
F
情境与问题
上体育课时,当某一排同学整理好队形,并执行完老师的口令 “向前三步走,向右看齐” 之后,同学们位移的方向是否相同?位移的大小是否相等?能否认为同学们的位移是相同的?
探索新知
可以认为,情境中同学们位移的方向和大小都相等,即位移相同.
相等向量: 的向量称为相等的向量.
大小相等、方向相同
向量 a 和 b 相等,记作:a=b .
探索新知
尝试与发现
下图中,相等的向量有
a=, .
a
b
B
A
D
C
d
c
F
E
典型例题
例 2 如图,已知四边形 ABCD,则“”
是“四边形 ABCD 为平行四边形”的什么条件?
解:如果 ,那就表示这两个向量的方向相同且大小相等;
由图可知 ABDC 且 AB∥DC,因此四边形 ABCD 为平行四边形.
反之,如果四边形 ABCD 为平行四边形,
则 ABDC 且 AB∥DC,则 .
综上,“”是“四边形 ABCD 为平行四边形”的充要条件.
典型例题
例 3 如图所示,O 是正六边形 ABCDEF 的中心,以图中字母为始点或终点,分别写出与向量 ,, 相等的向量.
解:因为两个向量相等,只要方向相同大小相等即可,因此
A
B
C
D
E
F
O
探索新知
共线向量
向量的平行:如果两个非零向量的方向 ,则称这两个向量平行,两个向量平行也称两个向量共线 .
对向量平行的理解
(1) 向量平行 (共线) 时,表示向量的有向线段所在的直线平行或重合.
(2) 向量共线中的“共线”的含义不是平面几何中的“共线”的含义.共线向量有四种情况:方向相同模相等;方向相同模不等;方向相反模相等;方向相反模不等.
(3) 任一向量 a 都与它本身平行.
相同或者相反
平行
规定:零向量与任意向量 .
记作:a ∥b .
典型例题
例 4 如图所示,找出其中共线的向量,并写出共线向量模之间的关系
解:不难看出
a
b
d
e
f
c
a∥c 且
b∥d 且
e∥f 且
当堂检测
当堂检测
B
当堂检测
D
当堂检测
BD
当堂检测
D
当堂检测
D
当堂检测
B
当堂检测
当堂检测
A
当堂检测
D
本节课学习了哪些知识点呢?
1. 向量的定义:方向、大小;
2. 向量的表示;
3. 特殊向量:单位向量、零向量;
4. 特殊关系:相等向量、共线向量.
感谢观看
祝同学新学期新气象
