2026年高考物理一轮复习 机械振动(含解析)
文档属性
| 名称 | 2026年高考物理一轮复习 机械振动(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-09 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
高考物理一轮复习 机械振动
一.选择题(共8小题)
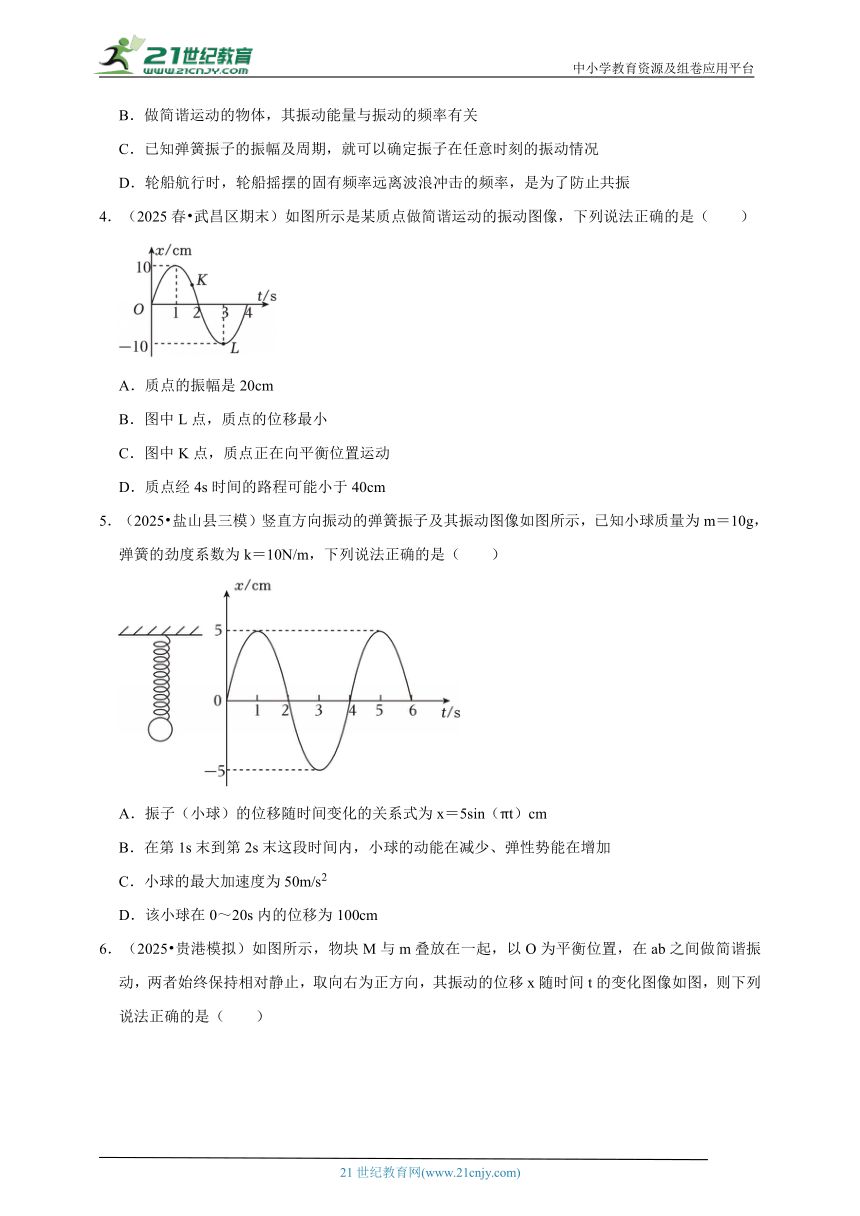
1.(2025春 武汉期末)如图甲所示,把一个得筛子用四根弹簧支撑起来,筛子上装一个电动偏心轮,它每转一周,给筛子一个驱动力,这就做成了一个共振筛,该共振筛的共振曲线如图乙所示。已知增大电压,可使偏心轮转速提高;增加筛子质量,可增大筛子的固有周期。现在,在某电压下偏心轮的转速是54r/min。下列说法正确的是( )
A.共振筛现在的振动频率为0.8Hz
B.仅增加筛子质量,可以使筛子的振幅增大
C.仅减小电压,可以使筛子的振幅增大
D.现在关闭电源直到共振筛静止前,共振筛振动的周期逐渐增大
2.(2025 临汾模拟)如图甲所示,质量M=5.0kg的箱子P放在水平地面上,两根相同的轻质弹簧连着质量m=1.0kg的小球Q,两弹簧另一端与箱子P连接,弹簧均处于竖直状态。取竖直向上为正方向,小球在竖直方向振动过程中相对平衡位置的位移y随时间t的变化如图乙所示,箱子P始终保持静止。已知两弹簧的劲度系数k=50N/m,重力加速度g=10m/s2,则( )
A.t1=0.05πs时,小球的加速度为零
B.t=0.1πs时.小球的速度为零
C.t2=0.15πs时,箱子P对地面的压力大小为64N
D.t2=0.15πs时.箱子P对地面的压力大小为56N
3.(2025春 武汉期末)下列关于机械振动的有关说法正确的是( )
A.单摆做简谐运动的回复力是由重力和摆线拉力的合力提供
B.做简谐运动的物体,其振动能量与振动的频率有关
C.已知弹簧振子的振幅及周期,就可以确定振子在任意时刻的振动情况
D.轮船航行时,轮船摇摆的固有频率远离波浪冲击的频率,是为了防止共振
4.(2025春 武昌区期末)如图所示是某质点做简谐运动的振动图像,下列说法正确的是( )
A.质点的振幅是20cm
B.图中L点,质点的位移最小
C.图中K点,质点正在向平衡位置运动
D.质点经4s时间的路程可能小于40cm
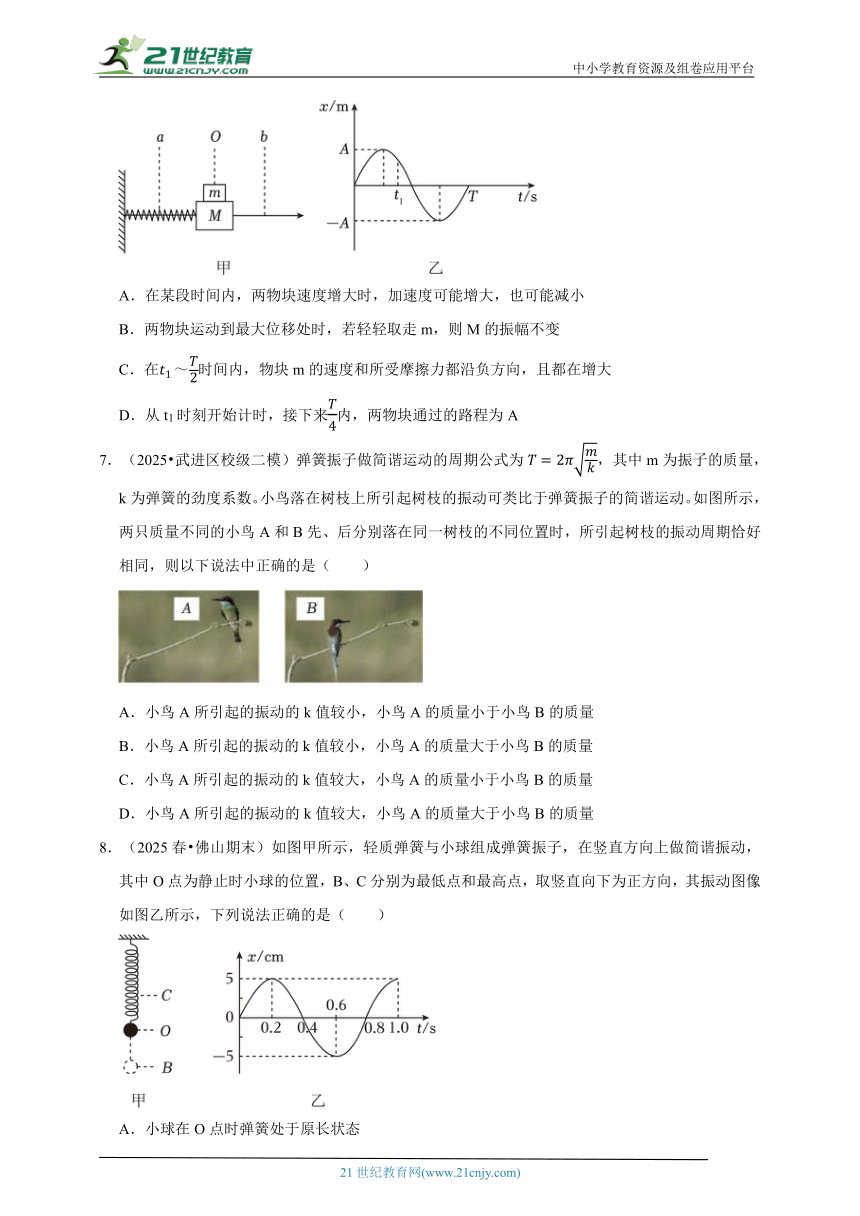
5.(2025 盐山县三模)竖直方向振动的弹簧振子及其振动图像如图所示,已知小球质量为m=10g,弹簧的劲度系数为k=10N/m,下列说法正确的是( )
A.振子(小球)的位移随时间变化的关系式为x=5sin(πt)cm
B.在第1s末到第2s末这段时间内,小球的动能在减少、弹性势能在增加
C.小球的最大加速度为50m/s2
D.该小球在0~20s内的位移为100cm
6.(2025 贵港模拟)如图所示,物块M与m叠放在一起,以O为平衡位置,在ab之间做简谐振动,两者始终保持相对静止,取向右为正方向,其振动的位移x随时间t的变化图像如图,则下列说法正确的是( )
A.在某段时间内,两物块速度增大时,加速度可能增大,也可能减小
B.两物块运动到最大位移处时,若轻轻取走m,则M的振幅不变
C.在时间内,物块m的速度和所受摩擦力都沿负方向,且都在增大
D.从t1时刻开始计时,接下来内,两物块通过的路程为A
7.(2025 武进区校级二模)弹簧振子做简谐运动的周期公式为,其中m为振子的质量,k为弹簧的劲度系数。小鸟落在树枝上所引起树枝的振动可类比于弹簧振子的简谐运动。如图所示,两只质量不同的小鸟A和B先、后分别落在同一树枝的不同位置时,所引起树枝的振动周期恰好相同,则以下说法中正确的是( )
A.小鸟A所引起的振动的k值较小,小鸟A的质量小于小鸟B的质量
B.小鸟A所引起的振动的k值较小,小鸟A的质量大于小鸟B的质量
C.小鸟A所引起的振动的k值较大,小鸟A的质量小于小鸟B的质量
D.小鸟A所引起的振动的k值较大,小鸟A的质量大于小鸟B的质量
8.(2025春 佛山期末)如图甲所示,轻质弹簧与小球组成弹簧振子,在竖直方向上做简谐振动,其中O点为静止时小球的位置,B、C分别为最低点和最高点,取竖直向下为正方向,其振动图像如图乙所示,下列说法正确的是( )
A.小球在O点时弹簧处于原长状态
B.t=0.2s时,弹簧振子的加速度为正向最大
C.t=0.2s到t=0.4s内,弹簧振子做加速度减小的变加速直线运动
D.在t=0.1s与t=0.7s时,弹簧振子的速度大小相等、方向相反
二.多选题(共4小题)
(多选)9.(2025春 武汉期末)手机是与他人联系时使用较多的工具。手机正在充电时,闹钟响起手机振动,充电线也跟着振动,若手机振动的频率为f1,振动的充电线上某点的频率为f2,如图所示。下列说法正确的是( )
A.充电线将做受迫振动,f1=f2
B.充电线上离手机充电口近的点先振动
C.手机振动的频率越大,充电线抖动幅度越大
D.同一手机,更换不同长度充电线,振动时的频率不同
(多选)10.(2025春 天津期中)图甲为竖直方向做简谐运动的弹簧振子,小物块的质量为m,弹簧振子的振动图像如图乙所示,以向上方向为x的正方向。下列说法正确的是( )
A.t1时刻物块的速度为0
B.t2时刻弹簧的弹力为0
C.t2﹣t3时间内,物块的加速度变小
D.t3﹣t4时间内,物块的速度方向向上
(多选)11.(2025 宝丰县三模)关于做简谐运动物体的平衡位置,下列叙述正确的是( )
A.是回复力为0的位置
B.是速度为0的位置
C.是势能最大的位置
D.是回复力产生的加速度改变方向的位置
(多选)12.(2025 山东模拟)如图所示,水平地面上固定光滑斜面的倾角为30°且长度足够长,一劲度系数为k且与斜面平行的轻质弹簧下端固定在斜面底端,上端与质量为m1的小球甲相连。一条不可伸长的轻绳绕过斜面顶端的轻质光滑定滑轮,一端连接小球甲,另一端连接一轻质挂钩。开始时轻绳处于恰好伸直状态,小球甲静止在A点。现在挂钩上挂质量为m的小球乙,并将其由静止释放,当弹簧第一次恢复原长时小球甲运动到B点(图中未画出),一段时间后,小球甲到达最高点C(图中未画出)。不计一切摩擦,弹簧始终在弹性限度内,小球甲不会和定滑轮相碰,小球乙不会和地面相碰,重力加速度大小为g,小球甲、乙均可视为质点,已知弹簧弹性势能满足Epkx2(x为弹簧形变量)。下列说法正确的是( )
A.若m1=m,则BC=3AB
B.若m1=2m,则BC=2AB
C.若m1=2m,则小球甲从A点运动到C点的过程中,最大速度为
D.若m1=m,则小球甲从A点运动到C点,弹簧弹性势能的变化量为
三.填空题(共4小题)
13.(2025 福建模拟)如图甲所示,将手机挂在轻弹簧下面,并将手机向下拉一小段距离后由静止释放,手机在竖直方向做简谐运动,手机软件记录其加速度变化情况如图乙所示,以竖直向上为正方向,则在0~0.2s内,手机运动的速度 (选填“增大”或“减小”);弹簧弹力在 s(选填“0.4”或“0.8”)时刻达到最大值。
14.(2025春 泉州期中)如图所示,一质点做简谐运动,O点为平衡位置,质点从M点以速度v0向右出发,然后以v0的速度第一次通过N点,历时2s,质点通过N点后再经过1s后,第2次通过N点,在这3s内质点通过的总路程为20cm。则质点做简谐运动的振幅为 cm,周期为 s。若质点从平衡位置O点出发,则经过0.5s,通过的路程为 cm。
15.(2025春 龙岩期中)如图所示,一质点做简谐运动,先后以相同的速度依次通过M、N两点,历时1s,质点通过N点后再经过1s又再次通过N点,在这2s内质点通过的总路程为12cm。则:质点从平衡位置O到N点的时间是 s,该质点的振动周期是 s,振幅是 cm。
16.(2024秋 思明区校级期末)上课时老师将一蜂鸣器系在轻绳的一端,然后使蜂鸣器迅速水平旋转,蜂鸣器的音调竟然发生忽高忽低的变化,则旋转时蜂鸣器发声的频率 (选填“不变”或“改变”),蜂鸣器音调变低时,蜂鸣器是向 (选填“靠近”或“远离”)同学们的方向运动。
四.解答题(共4小题)
17.(2025 浦口区校级模拟)如图所示,细线上端固定于O点,下端系质量为m小球构成单摆。小球在竖直平面内做简谐运动时动能Ek随时间t的变化关系如图所示,图中坐标为已知量,重力加速度为g,求:
(1)单摆的摆长;
(2)小球最大向心加速度。
18.(2025春 佛山期末)如图所示,劲度系数k=50N/m的轻弹簧左端固定,右端与静止在光滑水平面上的小球相连,将小球向右缓慢拉至C点后由静止释放,振子(小球)在水平面上的B、C两点之间做简谐运动,O点为平衡位置,P点为OC的中点。某次振子从左向右经过OC间的P点时开始计时,t=6.0s后振子第四次返回到P点,期间通过的路程s=48cm。求:
(1)该简谐运动的周期T和振幅A;
(2)振子经过P点时回复力的大小F。
19.(2025 泗阳县校级模拟)如图所示,劲度系数为k的轻弹簧一端固定在地面,另一端与质量为m的物体P连接,跨过定滑轮的轻绳一端与物体P连接,另一端与质量为2m的物体Q连接,重力加速度为g,用手托着物体Q使轻绳刚好伸直无张力,释放后物体P做简谐运动,经过时间t物体P的速度第一次达到最大。求:
(1)物体P做简谐运动的周期和振幅(周期用含t的式子表示);
(2)物体P的最大速度;
(3)在时间t内轻绳对物体Q拉力的冲量大小。
20.(2025 盐都区校级三模)某兴趣小组研究弹簧振子,设计了如图所示的装置,一个轻弹簧竖直放置,一端固定于地面,另一端与质量为m的物体B固连在一起,整个装置被一个口径略大且足够长的光滑圆套约束(图中未画出),现将质量也为m的物体A由B的正上方某一高度处自由释放,A和B发生碰撞后两者一起以相同的速度向下运动(但不粘连),AB在以后的振动过程中恰好不会分离,弹簧的劲度系数为k,整个振动过程弹簧处于弹性限度内,忽略A、B的体积,不计空气阻力,m、k、g为已知量,求:
(1)AB一起振动过程中最大加速度的大小;
(2)小组中的甲同学通过研究弹簧弹力做功,得出了弹簧的弹性势能表达式(x为弹簧形变量),求A释放前距B的高度;
(3)已知AB一起振动的周期为T,以A与B碰撞为计时起点,求AB振动到最高点的时刻。
高考物理一轮复习 机械振动
参考答案与试题解析
一.选择题(共8小题)
1.(2025春 武汉期末)如图甲所示,把一个得筛子用四根弹簧支撑起来,筛子上装一个电动偏心轮,它每转一周,给筛子一个驱动力,这就做成了一个共振筛,该共振筛的共振曲线如图乙所示。已知增大电压,可使偏心轮转速提高;增加筛子质量,可增大筛子的固有周期。现在,在某电压下偏心轮的转速是54r/min。下列说法正确的是( )
A.共振筛现在的振动频率为0.8Hz
B.仅增加筛子质量,可以使筛子的振幅增大
C.仅减小电压,可以使筛子的振幅增大
D.现在关闭电源直到共振筛静止前,共振筛振动的周期逐渐增大
【考点】共振及其应用;阻尼振动和受迫振动.
【专题】定性思想;推理法;简谐运动专题;推理论证能力.
【答案】C
【分析】根据振动周期和频率关系列式,结合共振曲线进行分析解答。
【解答】解:A.共振筛现在的振动周期为Ts≈1.11s,则振动频率为f,解得f=0.9Hz,故A错误;
BC.由图乙可知,筛子固有频率为0.8Hz,减小电压会降低偏心轮转速,偏心轮的频率减小,则筛子固有频率和驱动力频率的差值变小,筛子振幅增大,增加筛子质量,筛子的固有周期增大,则固有频率减小,则固有频率和驱动力频率的差值变大,筛子振幅减小,故B错误,C正确;
D.关闭电源后共振筛自由振动,直到共振筛静止前,共振筛振动的周期不变,故D错误。
故选:C。
【点评】考查振动周期和频率关系列式,共振曲线的理解,会根据题意进行准确分析解答。
2.(2025 临汾模拟)如图甲所示,质量M=5.0kg的箱子P放在水平地面上,两根相同的轻质弹簧连着质量m=1.0kg的小球Q,两弹簧另一端与箱子P连接,弹簧均处于竖直状态。取竖直向上为正方向,小球在竖直方向振动过程中相对平衡位置的位移y随时间t的变化如图乙所示,箱子P始终保持静止。已知两弹簧的劲度系数k=50N/m,重力加速度g=10m/s2,则( )
A.t1=0.05πs时,小球的加速度为零
B.t=0.1πs时.小球的速度为零
C.t2=0.15πs时,箱子P对地面的压力大小为64N
D.t2=0.15πs时.箱子P对地面的压力大小为56N
【考点】简谐运动的图像问题.
【专题】定量思想;推理法;振动图象与波动图象专题;推理论证能力.
【答案】C
【分析】回复力最大,加速度为最大;
平衡位置处,速度为最大;
根据平衡条件列式,求x,t2=0.15πs时刻,偏离平衡位置的位移为A,根据平衡条件结合牛顿第三定律,求箱子对地面的压力。
【解答】解:A.t1=0.05πs时刻小球在正向最大位移处,回复力最大,由牛顿第二定律,加速度为最大,故A错误;
B.t=0.1πs时刻小球在平衡位置处,速度为最大,故B错误;
CD.两弹簧相同,Q静止时,上方弹簧伸长,下方弹簧压缩,设弹簧形变量为x,根据平衡条件有2kx=m2g
解得x=0.1m
由图乙知t2=0.15πs时刻小球在最低点,偏离平衡位置的位移为A,此时上方弹簧拉伸到更长,下方弹簧压缩到更短,根据平衡条件,对箱子有FN=Mg+2k(A+x),代入数据解得FN=64N
由牛顿第三定律知箱子对地面的压力为64N,故C正确,D错误。
故选:C。
【点评】本题解题关键要掌握不同位置的速度加速度位移特征,位移为零时,加速度最小速度最大,位移最大时加速度最大速度最小。
3.(2025春 武汉期末)下列关于机械振动的有关说法正确的是( )
A.单摆做简谐运动的回复力是由重力和摆线拉力的合力提供
B.做简谐运动的物体,其振动能量与振动的频率有关
C.已知弹簧振子的振幅及周期,就可以确定振子在任意时刻的振动情况
D.轮船航行时,轮船摇摆的固有频率远离波浪冲击的频率,是为了防止共振
【考点】共振及其应用;简谐运动的定义、运动特点与判断;单摆及单摆的条件.
【专题】定性思想;推理法;单摆问题;推理论证能力.
【答案】D
【分析】根据回复力、振幅以及振动方程和共振的防止和利用进行分析解答。
【解答】解:A.单摆做简谐运动的回复力是由重力沿切线方向的分力提供,故A错误;
B.做简谐运动的物体,其振动能量与振动的振幅有关,故B错误;
C.已知弹簧振子的振幅及周期,并不能确定振子在任意时刻的振动情况,必须利用振动方程才能确定,故C错误;
D.轮船航行时,轮船摇摆的固有频率远离波浪冲击的频率,是为了防止共振,故D正确。
故选:D。
【点评】考查回复力、振幅以及振动方程和共振的防止和利用,会根据题意进行准确分析解答。
4.(2025春 武昌区期末)如图所示是某质点做简谐运动的振动图像,下列说法正确的是( )
A.质点的振幅是20cm
B.图中L点,质点的位移最小
C.图中K点,质点正在向平衡位置运动
D.质点经4s时间的路程可能小于40cm
【考点】简谐运动的图像问题.
【专题】定性思想;推理法;振动图象与波动图象专题;理解能力.
【答案】C
【分析】根据图像可知振幅、L的位置和M的振动方向;质点经一个周期通过的路程为4A。
【解答】解:A、根据图像可知,质点的振幅是10cm,故A错误;
B、图中L点处于波谷,质点的位移最大,故B错误;
C、有图可知,图中K点,质点正在向平衡位置运动,故C正确;
D、质点经4s时间(即一个周期)通过的路程为:s=4A=4×10cm=40cm,故D错误。
故选:C。
【点评】本题主要是考查了振动的图像;解答此类问题的关键是要理解振动图像的物理意义,能够根据图像直接读出振幅和质点的振动方向。
5.(2025 盐山县三模)竖直方向振动的弹簧振子及其振动图像如图所示,已知小球质量为m=10g,弹簧的劲度系数为k=10N/m,下列说法正确的是( )
A.振子(小球)的位移随时间变化的关系式为x=5sin(πt)cm
B.在第1s末到第2s末这段时间内,小球的动能在减少、弹性势能在增加
C.小球的最大加速度为50m/s2
D.该小球在0~20s内的位移为100cm
【考点】简谐运动的回复力;简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定量思想;归纳法;简谐运动专题;分析综合能力.
【答案】C
【分析】根据图像得到振幅和周期,然后求出角速度,便可得到位移随时间变化的关系式;简谐运动过程中动能和势能相互转化,可根据图像确定转化情况;根据F=kA求出最大弹力,根据牛顿第二定律可求出小球的最大加速度;首先求出20s为多少周期,再求位移。
【解答】解:A.由图可知,小球振动的周期T为4s,振幅A为5cm,则小球的位移随时间变化的关系式为
故A错误;
B.小球在最大位移处速度为零,弹簧弹性势能最大,所以在第1s末到第2s末这段时间内,小球从最大位移运动到平衡位置,则小球的动能在增加、弹性势能在减小,故B错误;
C.小球在最大位移处时受到的弹力最大为
F=kA=10N/m×5×10﹣2m=0.5N
则根据牛顿第二定律可得,小球的最大加速度为
故C正确;
D.由图可知,小球周期为4s,20s即为4个周期,所以该小球在0~20s内的位移为零,故D错误。
故选:C。
【点评】本题关键是可以从简谐运动图像中获取基本信息,然后结合简谐运动的周期性及牛顿第二定律求解即可。
6.(2025 贵港模拟)如图所示,物块M与m叠放在一起,以O为平衡位置,在ab之间做简谐振动,两者始终保持相对静止,取向右为正方向,其振动的位移x随时间t的变化图像如图,则下列说法正确的是( )
A.在某段时间内,两物块速度增大时,加速度可能增大,也可能减小
B.两物块运动到最大位移处时,若轻轻取走m,则M的振幅不变
C.在时间内,物块m的速度和所受摩擦力都沿负方向,且都在增大
D.从t1时刻开始计时,接下来内,两物块通过的路程为A
【考点】简谐运动过程中速度、加速度(回复力)与位移的变化问题;简谐运动的某一时刻或某段时间内质点的运动情况;简谐运动的图像问题.
【专题】定性思想;推理法;振动图象与波动图象专题;推理论证能力.
【答案】B
【分析】在最大位移处,加速度最大,静摩擦力最大。由图像可读出振子振动的周期和振幅,振子向平衡位置运动的过程中,速度增大,加速度减小。通过分析振子位移的变化,即可判断其速度和加速度的变化。
【解答】解:A.物块速度增大时,物块向平衡位置运动,则物块的位移减小,据简谐振动的受力特点F=﹣kx,加速度减小,故A错误;
B.简谐运动是一种无能量损失的振动,它只是动能和势能间的转化,总机械能守恒。其能量只有振幅决定,即振幅不变,振动系统能量不变。当将m在最大位移处轻轻取走,说明m取走时动能为零,m取走前后M振幅没有改变,振动系统机械能总量不变,故B正确。
C.由物体振动的位移x随时间t的变化图像可知在时间内,由图像的斜率为负且增大可知,物块m的速度沿负方向在增大,受摩擦力方向沿负方向,据F=﹣kx可知,位移x在减小,回复力减小,加速度在减小,所以摩擦力在减小,故C错误;
D.由振动的位移x随时间t的变化图像知,两物块在平衡位置速度最大,因此两物块从b→O的平均速率要小于从t1开始经时间内的平均速率,所以从t1开始经通过的路程大于A,故D错误。
故选:B。
【点评】解答该题的关键是弄清m的恢复力的来源以及注意最大位移处将一质量为m的物块轻轻地拿走表示的是小物块拿走时水平方向的速度为0,此时无机械能损失。
7.(2025 武进区校级二模)弹簧振子做简谐运动的周期公式为,其中m为振子的质量,k为弹簧的劲度系数。小鸟落在树枝上所引起树枝的振动可类比于弹簧振子的简谐运动。如图所示,两只质量不同的小鸟A和B先、后分别落在同一树枝的不同位置时,所引起树枝的振动周期恰好相同,则以下说法中正确的是( )
A.小鸟A所引起的振动的k值较小,小鸟A的质量小于小鸟B的质量
B.小鸟A所引起的振动的k值较小,小鸟A的质量大于小鸟B的质量
C.小鸟A所引起的振动的k值较大,小鸟A的质量小于小鸟B的质量
D.小鸟A所引起的振动的k值较大,小鸟A的质量大于小鸟B的质量
【考点】简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定性思想;归纳法;简谐运动专题;理解能力.
【答案】A
【分析】根据弹簧振子做简谐运动的周期公式分析即可。
【解答】解:两小鸟引起振动的周期相同,但枝头处的k相对较小,根据简谐运动的周期公式可知,枝头处小鸟的质量较小,故A正确,BCD错误。
故选:A。
【点评】知道枝头处的k相对较小是解题的关键。
8.(2025春 佛山期末)如图甲所示,轻质弹簧与小球组成弹簧振子,在竖直方向上做简谐振动,其中O点为静止时小球的位置,B、C分别为最低点和最高点,取竖直向下为正方向,其振动图像如图乙所示,下列说法正确的是( )
A.小球在O点时弹簧处于原长状态
B.t=0.2s时,弹簧振子的加速度为正向最大
C.t=0.2s到t=0.4s内,弹簧振子做加速度减小的变加速直线运动
D.在t=0.1s与t=0.7s时,弹簧振子的速度大小相等、方向相反
【考点】简谐运动的图像问题;简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定性思想;推理法;简谐运动专题;理解能力.
【答案】C
【分析】根据弹簧振子振动特点结合振动图像进行逐项分析。
【解答】解:A、O点为静止时小球的位置,小球在O点时弹簧处于伸长状态,故A错误;
B、t=0.2s时,弹簧振子处于下方振幅处,根据a可知,加速度为负向最大,故B错误;
C、t=0.2s到t=0.4s内,弹簧振子的位移减小、速度最大、加速度减小,所以,振子做加速度减小的变加速直线运动,故C正确;
D、根据图乙可知,在t=0.1s与t=0.7s时,弹簧振子的速度大小相等、方向相同,故D错误。
故选:C。
【点评】本题主要是考查了简谐运动的知识;知道简谐运动的平衡位置是物体静止时受力平衡的位置;振动的质点在振动过程中各物理量的变化情况可以这样分析:位移增大→回复力增大→加速度增大→速度减小→动能减小→势能增大。
二.多选题(共4小题)
(多选)9.(2025春 武汉期末)手机是与他人联系时使用较多的工具。手机正在充电时,闹钟响起手机振动,充电线也跟着振动,若手机振动的频率为f1,振动的充电线上某点的频率为f2,如图所示。下列说法正确的是( )
A.充电线将做受迫振动,f1=f2
B.充电线上离手机充电口近的点先振动
C.手机振动的频率越大,充电线抖动幅度越大
D.同一手机,更换不同长度充电线,振动时的频率不同
【考点】共振及其应用.
【专题】定性思想;推理法;简谐运动专题;推理论证能力.
【答案】AB
【分析】根据受迫振动和共振的特点进行分析解答。
【解答】解:AD.共振闹钟响起手机振动,充电线也跟着振动,可知充电线做受迫振动,则有f1=f2,由于受迫振动的频率取决于驱动力的频率,所以同一手机,更换不同长度充电线,振动时的频率相同,故A正确,D错误。
B.充电线上越靠近振源位置的点越先振动,所以充电线上离手机充电口近的点先振动,故B正确;
C.当手机振动的频率等于充电线振动的固有频率时,充电线抖动幅度最大,所以手机振动的频率越大,充电线抖动幅度不一定越大,故C错误。
故选:AB。
【点评】考查受迫振动和共振的特点,会根据题意进行准确分析解答。
(多选)10.(2025春 天津期中)图甲为竖直方向做简谐运动的弹簧振子,小物块的质量为m,弹簧振子的振动图像如图乙所示,以向上方向为x的正方向。下列说法正确的是( )
A.t1时刻物块的速度为0
B.t2时刻弹簧的弹力为0
C.t2﹣t3时间内,物块的加速度变小
D.t3﹣t4时间内,物块的速度方向向上
【考点】简谐运动的表达式及振幅、周期、频率、相位等参数;简谐运动的回复力.
【专题】定性思想;推理法;简谐运动专题;推理论证能力.
【答案】AD
【分析】根据位移图像的斜率等于速度,分析速度的大小和方向;根据图像读出位移,进而分析振子的加速度大小及方向。
【解答】解:A、由图像可知,t1时刻物块处于最大位移处,则速度为零,故A正确;
B、t2时刻物块在平衡位置处,回复力等于零,所以此时弹簧的弹力等于物块的重力,故B错误;
C、由图可知t3时刻物块处于负向的最大位移处,所以在t2﹣t3时间内,物块由平衡位置向下运动到负向的最大位移处,位移逐渐增大,则加速度逐渐增大,故C错误;
D、t3时刻物块处于负向的最大位移处,所以在t3﹣t4时间内,物块由负向的最大位移处运动到平衡位置处,速度向上,故D正确。
故选:AD。
【点评】解决该题需熟练掌握简谐运动的运动过程,会根据振动图像判断位移和速度的变化情况。
(多选)11.(2025 宝丰县三模)关于做简谐运动物体的平衡位置,下列叙述正确的是( )
A.是回复力为0的位置
B.是速度为0的位置
C.是势能最大的位置
D.是回复力产生的加速度改变方向的位置
【考点】简谐运动的回复力;简谐运动的定义、运动特点与判断.
【专题】定性思想;推理法;简谐运动专题;理解能力;推理论证能力.
【答案】AD
【分析】做简谐运动物体的回复力F=﹣kx,x表示物体偏离平衡位置的距离,平衡位置处物体的加速度为零,速度最大,势能最小。
【解答】解:A、做简谐运动物体的回复力F=﹣kx,x表示物体偏离平衡位置的距离,物体在平衡位置时,x=0,所以平衡位置是回复力为零的位置,故A正确,
BC、平衡位置物体的加速度为零,速度最大,势能最小,故BC错误,
D、平衡位置处物体的加速度为零,该位置为回复力产生加速度方向改变的位置,故D正确,
故选:AD。
【点评】本题考查平衡位置的理解,注意概念的学习。
(多选)12.(2025 山东模拟)如图所示,水平地面上固定光滑斜面的倾角为30°且长度足够长,一劲度系数为k且与斜面平行的轻质弹簧下端固定在斜面底端,上端与质量为m1的小球甲相连。一条不可伸长的轻绳绕过斜面顶端的轻质光滑定滑轮,一端连接小球甲,另一端连接一轻质挂钩。开始时轻绳处于恰好伸直状态,小球甲静止在A点。现在挂钩上挂质量为m的小球乙,并将其由静止释放,当弹簧第一次恢复原长时小球甲运动到B点(图中未画出),一段时间后,小球甲到达最高点C(图中未画出)。不计一切摩擦,弹簧始终在弹性限度内,小球甲不会和定滑轮相碰,小球乙不会和地面相碰,重力加速度大小为g,小球甲、乙均可视为质点,已知弹簧弹性势能满足Epkx2(x为弹簧形变量)。下列说法正确的是( )
A.若m1=m,则BC=3AB
B.若m1=2m,则BC=2AB
C.若m1=2m,则小球甲从A点运动到C点的过程中,最大速度为
D.若m1=m,则小球甲从A点运动到C点,弹簧弹性势能的变化量为
【考点】简谐运动的能量问题;简谐运动过程中速度、加速度(回复力)与位移的变化问题;简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定量思想;方程法;简谐运动专题;机械能守恒定律应用专题;推理论证能力.
【答案】AC
【分析】根据受力平衡求出开始时弹簧的压缩量和平衡位置处弹簧的压缩量,然后结合简谐振动的对称性分析BC与AB的关系;当小球受到的合外力等于零时,小球的速度最大,由此结合弹簧弹性势能的公式求出;根据机械能守恒求出。
【解答】解:甲、乙两球与弹簧构成的系统机械能守恒,可知甲、乙两球的运动是简谐运动,没有悬挂小球乙时,弹簧处于压缩状态,对小球甲有m1gsin 30°=kx1
解得x1
根据简谐运动的特征,小球甲运动到平衡位置O点时所受合力为零,有mg=m1gsin 30°+kx2
解得x2
A、若m1=m,则小球甲运动到平衡位置O点时有x2=x1,弹簧处于拉伸状态,可知平衡位置O点在弹簧原长B位置的上方,根据简谐运动的对称性规律可知AO=AB+BO=x1+x2=OC,如图
则BC=BO+OC=x1+2x23AB,故A正确;
B、若m1=2m,小球甲运动到平衡位置O点时x'2=0,弹簧处于原长,可知平衡位置O点在弹簧原长B位置处,根据简谐运动的对称性规律可知 AO=AB=OC,则BC=AB,故B错误;
C、若m1=2m,小球甲从A 点运动到C点的过程中,小球甲运动到平衡位置O点时速度最大,小球甲从A点运动到O点弹簧的形变量从x1变为x'2=0,弹性势能减小,根据能量守恒定律有ΔE'p+mgx1(2m+m)2mgx1sin 30°
其中ΔE'pk
解得vm,故C正确。
D、若m1=m,小球甲从A点运动到C点,根据能量守恒定律有ΔEp=mg 2(x1+x2)﹣mg 2(x1+x2)sin 30°
解得ΔEp,故D错误;
故选:AC。
【点评】对于简谐振动的问题,抓住简谐振动的对称性,以及正确判断平衡位置是关键。
三.填空题(共4小题)
13.(2025 福建模拟)如图甲所示,将手机挂在轻弹簧下面,并将手机向下拉一小段距离后由静止释放,手机在竖直方向做简谐运动,手机软件记录其加速度变化情况如图乙所示,以竖直向上为正方向,则在0~0.2s内,手机运动的速度 增大 (选填“增大”或“减小”);弹簧弹力在 0.8 s(选填“0.4”或“0.8”)时刻达到最大值。
【考点】简谐运动过程中速度、加速度(回复力)与位移的变化问题;简谐运动的回复力.
【专题】定量思想;方程法;简谐运动专题;推理论证能力.
【答案】增大;0.8。
【分析】根据做简谐运动的物体远离平衡位置,加速度越大,速度越小分析;由受力分析和牛顿第二定律可知弹簧弹力大小。
【解答】解:从t=0至t=0.2s过程,手机的加速度减小,可知手机从最大位移处向平衡位置运动,手机的速度增大。
根据a,结合以竖直向上为正方向可知,在t=0.8s时刻手机位于最高点,弹簧的弹力与重力的和提供向心力,即kA=mg+kx;而t=0.8s时刻手机位于最低点,弹簧弹力减去重力的差提供向心力,即kA=kx′﹣mg,对比可知在t=0.8s时刻弹簧的弹力达到最大。
故答案为:增大;0.8。
【点评】本题考查了简谐运动的图像问题、简谐运动的特点,解题的关键是知道简谐运动加速度方向始终指向平衡位置,加速度方向与相对平衡位置的位移的方向始终相反。
14.(2025春 泉州期中)如图所示,一质点做简谐运动,O点为平衡位置,质点从M点以速度v0向右出发,然后以v0的速度第一次通过N点,历时2s,质点通过N点后再经过1s后,第2次通过N点,在这3s内质点通过的总路程为20cm。则质点做简谐运动的振幅为 10 cm,周期为 6 s。若质点从平衡位置O点出发,则经过0.5s,通过的路程为 5 cm。
【考点】简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定量思想;方程法;简谐运动专题;推理论证能力.
【答案】10;6;5。
【分析】简谐运动的质点,先后以同样大小的速度通过M、N两点,则可判定这两点关于平衡位置对称,根据对称性可求解;根据振动方程求解。
【解答】解:质点先后以相同的速度依次通过M、N两点,可知M、N两点关于平衡位置O点对称,所以质点由M到O时间与由O到N的时间相等,则质点从平衡位置O到N点的时间t1=1s
因过N点后再经过1s质点以方向相反、大小相同的速度再次通过N点,则有从N点到最大位置的时间t2=0.5s
因此,质点振动的周期是T=4×(t1+t2)
代入数据得T=6s
3s为半个周期,质点在半个周期内总路程等于2倍振幅,所以振幅Acm=10cm
质点从平衡位置O点出发,则经过0.5s,则质点的位移x=Asin()=10×sin()cm=5cm
可知在这0.5s时间内质点的路程也是5cm
故答案为:质点从平衡位置O点出发,则经过0.5s,
【点评】本题考查简谐运动的相关问题,考查知识点针对性强,难度较小,考查了学生掌握知识与应用知识的能力。
15.(2025春 龙岩期中)如图所示,一质点做简谐运动,先后以相同的速度依次通过M、N两点,历时1s,质点通过N点后再经过1s又再次通过N点,在这2s内质点通过的总路程为12cm。则:质点从平衡位置O到N点的时间是 0.5 s,该质点的振动周期是 4 s,振幅是 6 cm。
【考点】简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定量思想;方程法;简谐运动专题;推理论证能力.
【答案】0.5,4,6。
【分析】简谐运动的质点,先后以同样大小的速度通过M、N两点,则可判定这两点关于平衡位置对称,根据对称性可求解。
【解答】解:质点做简谐运动,先后以相同的速度依次通过M、N两点,历时1s,过N点后再经过t=1s质点以方向相反、大小相同的速度再次通过N点,可知开始时质点运动的方向向右;质点先后以相同的速度依次通过M、N两点,可知M、N两点关于平衡位置O点对称,所以质点由M到O点的时间与由O到N的时间相等,那么平衡位置O到N点的时间t1=0.5s。因过N点后再经过t=1s质点以方向相反、大小相同的速度再次通过N点,则质点从N点到最大位置的时间t2=0.5s;因此质点振动的周期是T=4×(t1+t2),代入数据得T=4s;
结合以上的分析,可知质点从M到N,然后以相反的方向再到N恰好经过了半个周期,则质点总路程的一半,即为振幅,所以振幅Acm=6cm。
故答案为:0.5,4,6。
【点评】本题考查简谐运动的相关问题,考查知识点针对性强,难度较小,考查了学生掌握知识与应用知识的能力。
16.(2024秋 思明区校级期末)上课时老师将一蜂鸣器系在轻绳的一端,然后使蜂鸣器迅速水平旋转,蜂鸣器的音调竟然发生忽高忽低的变化,则旋转时蜂鸣器发声的频率 不变 (选填“不变”或“改变”),蜂鸣器音调变低时,蜂鸣器是向 远离 (选填“靠近”或“远离”)同学们的方向运动。
【考点】共振及其应用.
【专题】定性思想;推理法;波的多解性;推理论证能力.
【答案】不变;远离。
【分析】振源与观察者之间存在着相对运动,使观察者听到的声音频率不同于振源频率的现象,这就是频移现象。因为,声源相对于观测者在运动时,观测者所听到的声音会发生变化,当声源离观测者而去时,声波的波长增加,音调变得低沉,当声源接近观测者时,声波的波长减小,音调就变高。
【解答】解:旋转时蜂鸣器发声的频率不变。根据多普勒效应,当蜂鸣器向远离同学们的方向运动时,同学们听到声音的频率变小,即音调变低。
故答案为:不变;远离。
【点评】本题考查多普勒效应,知道在波源与观察者靠近时,观察者接收到的波的频率变高,而在波源与观察者远离时接收的频率变低,即高亢表示远离,低沉表示靠近。
四.解答题(共4小题)
17.(2025 浦口区校级模拟)如图所示,细线上端固定于O点,下端系质量为m小球构成单摆。小球在竖直平面内做简谐运动时动能Ek随时间t的变化关系如图所示,图中坐标为已知量,重力加速度为g,求:
(1)单摆的摆长;
(2)小球最大向心加速度。
【考点】单摆的能量转化;向心加速度的表达式及影响向心加速度大小的因素.
【专题】计算题;学科综合题;定量思想;方程法;单摆问题;推理论证能力.
【答案】(1)单摆的摆长为;
(2)小球最大向心加速度为。
【分析】(1)根据题图解得周期,结合周期公式解得摆长;
(2)根据向心加速度的公式解答。
【解答】解:(1)摆球一个周期内两次经过最低点,则一个周期内两次动能最大,由图可知,单摆的周期T=4t0
根据单摆周期公式
解得
(2)摆球到最低点的动能
速度最大时对应向心加速度的最大值
得
答:(1)单摆的摆长为;
(2)小球最大向心加速度为。
【点评】本题考查单摆周期公式的应用,解题关键掌握单摆的周期公式的运用。
18.(2025春 佛山期末)如图所示,劲度系数k=50N/m的轻弹簧左端固定,右端与静止在光滑水平面上的小球相连,将小球向右缓慢拉至C点后由静止释放,振子(小球)在水平面上的B、C两点之间做简谐运动,O点为平衡位置,P点为OC的中点。某次振子从左向右经过OC间的P点时开始计时,t=6.0s后振子第四次返回到P点,期间通过的路程s=48cm。求:
(1)该简谐运动的周期T和振幅A;
(2)振子经过P点时回复力的大小F。
【考点】简谐运动的回复力;简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定量思想;方程法;简谐运动专题;理解能力.
【答案】(1)该简谐运动的周期为3s和振幅6cm;
(2)振子经过P点时回复力的大小1.5N。
【分析】通过给定的时间和振子返回特定点的次数来确定简谐运动的周期。
利用振子在特定时间内通过的总路程来计算振幅。
根据振子在P点的位置,利用回复力的定义计算回复力的大小。
【解答】解:(1)根据题意有
t=2T
解得
T=3s
根据题意有
s=8A
解得
A=6cm
(2)振子经过P点时偏离平衡位置O的位移大小
根据回复力公式有
F=kx
解得
F=1.5N
答:(1)该简谐运动的周期为3s和振幅6cm;
(2)振子经过P点时回复力的大小1.5N。
【点评】此题考查了简谐运动的基本概念,包括周期、振幅的计算以及回复力的计算。
19.(2025 泗阳县校级模拟)如图所示,劲度系数为k的轻弹簧一端固定在地面,另一端与质量为m的物体P连接,跨过定滑轮的轻绳一端与物体P连接,另一端与质量为2m的物体Q连接,重力加速度为g,用手托着物体Q使轻绳刚好伸直无张力,释放后物体P做简谐运动,经过时间t物体P的速度第一次达到最大。求:
(1)物体P做简谐运动的周期和振幅(周期用含t的式子表示);
(2)物体P的最大速度;
(3)在时间t内轻绳对物体Q拉力的冲量大小。
【考点】简谐运动的表达式及振幅、周期、频率、相位等参数;弹簧类问题中的机械能守恒;动量定理的内容和应用.
【专题】定量思想;推理法;机械能守恒定律应用专题;动量定理应用专题;推理论证能力.
【答案】(1)物体P做简谐运动的周期为4t,振幅为;
(2)物体P的最大速度为;
(3)在时间t内轻绳对物体Q拉力的冲量大小为。
【分析】(1)从速度为0到第一次达到最大经过的时间是,求周期,根据弹力和重力平衡列式,求压缩量x1,当物体P的速度最大时加速度为0,合力为零,根据平衡列式,求伸长量x2,确定振幅;
(2)根据系统的机械能守恒列式,求速度;
(3)根据动量定理,求在时间t内轻绳对物体Q拉力的冲量大小。
【解答】解:(1)对物体P分析,从速度为0到第一次达到最大经过的时间是,则有
解得
T=4t
物体P从速度为0到第一次达到最大走过的位移大小是A,A是振幅,设刚释放时弹簧的压缩量为x1,弹力和重力平衡,则有
kx1=mg
解得
当物体P的速度最大时加速度为0,合力为零,设此时弹簧的伸长量为x2,根据平衡列式则有
kx2+mg=2mg
解得
振幅
(2)从释放到物体P速度首次达到最大,弹簧开始的压缩量和最后的伸长量相等,弹簧弹性势能相等,设最大速度为v,根据系统的机械能守恒得
代入得
(3)设在时间t内轻绳对物体Q拉力的冲量大小为I,以向下为正方向,根据动量定理得
2mgt﹣I=2mv
代入得
答:(1)物体P做简谐运动的周期为4t,振幅为;
(2)物体P的最大速度为;
(3)在时间t内轻绳对物体Q拉力的冲量大小为。
【点评】本题解题关键是掌握系统的机械能守恒定律、动量定理等,具有一定综合性,难度中等。
20.(2025 盐都区校级三模)某兴趣小组研究弹簧振子,设计了如图所示的装置,一个轻弹簧竖直放置,一端固定于地面,另一端与质量为m的物体B固连在一起,整个装置被一个口径略大且足够长的光滑圆套约束(图中未画出),现将质量也为m的物体A由B的正上方某一高度处自由释放,A和B发生碰撞后两者一起以相同的速度向下运动(但不粘连),AB在以后的振动过程中恰好不会分离,弹簧的劲度系数为k,整个振动过程弹簧处于弹性限度内,忽略A、B的体积,不计空气阻力,m、k、g为已知量,求:
(1)AB一起振动过程中最大加速度的大小;
(2)小组中的甲同学通过研究弹簧弹力做功,得出了弹簧的弹性势能表达式(x为弹簧形变量),求A释放前距B的高度;
(3)已知AB一起振动的周期为T,以A与B碰撞为计时起点,求AB振动到最高点的时刻。
【考点】简谐运动的某一时刻或某段时间内质点的运动情况;牛顿第二定律的简单应用;动量守恒与能量守恒共同解决实际问题.
【专题】定量思想;推理法;振动图象与波动图象专题;机械能守恒定律应用专题;推理论证能力.
【答案】(1)AB一起振动过程中最大加速度的大小为g;
(2)A释放前距B的高度为;
(3)AB振动到最高点的时刻为。
【分析】(1)根据牛顿第二定律,求加速度最大值;
(2)根据受力平衡列式,结合机械能守恒和碰撞过程的动量守恒,求h。
(3)确定振幅,写振动方程,根据AB碰撞位置,求时间,确定AB振动到最高点的时刻。
【解答】解:(1)AB在以后的振动过程中恰好不会分离,所以振动最高点为弹簧原长位置,此时加速度最大.根据牛顿第二定律有2mg=2ma
解得a=g
(2)B静止时,根据受力平衡有kx0=mg
物体A自由下落的过程,由机械能守恒得
物体A、B碰撞过程,根据动量守恒有mv0=2mv
碰后AB在以后振动过程中到达最高点时弹簧刚好处于原长状态,相对于原来向上运动得距离
对物体A、B和弹簧组成的系统,由能量守恒得
联立解得
(3)在振动过程中,设平衡位置弹簧的压缩量为x,有2mg=kx
振幅
以第一次向下经过平衡位置为0时刻,取向下为正方向,则振动方程为y=Asinωt
AB碰撞时y1=Asinωt1=x﹣x0
解得
因此以A与B碰撞为时起点,求AB振动到最高点的时刻
答:(1)AB一起振动过程中最大加速度的大小为g;
(2)A释放前距B的高度为;
(3)AB振动到最高点的时刻为。
【点评】本题解题关键是掌握受力平衡、碰撞中的动量守恒,系统的能量转化和守恒规律,能够正确书写振动方程,根据位置,确定时刻,难度中等。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
高考物理一轮复习 机械振动
一.选择题(共8小题)
1.(2025春 武汉期末)如图甲所示,把一个得筛子用四根弹簧支撑起来,筛子上装一个电动偏心轮,它每转一周,给筛子一个驱动力,这就做成了一个共振筛,该共振筛的共振曲线如图乙所示。已知增大电压,可使偏心轮转速提高;增加筛子质量,可增大筛子的固有周期。现在,在某电压下偏心轮的转速是54r/min。下列说法正确的是( )
A.共振筛现在的振动频率为0.8Hz
B.仅增加筛子质量,可以使筛子的振幅增大
C.仅减小电压,可以使筛子的振幅增大
D.现在关闭电源直到共振筛静止前,共振筛振动的周期逐渐增大
2.(2025 临汾模拟)如图甲所示,质量M=5.0kg的箱子P放在水平地面上,两根相同的轻质弹簧连着质量m=1.0kg的小球Q,两弹簧另一端与箱子P连接,弹簧均处于竖直状态。取竖直向上为正方向,小球在竖直方向振动过程中相对平衡位置的位移y随时间t的变化如图乙所示,箱子P始终保持静止。已知两弹簧的劲度系数k=50N/m,重力加速度g=10m/s2,则( )
A.t1=0.05πs时,小球的加速度为零
B.t=0.1πs时.小球的速度为零
C.t2=0.15πs时,箱子P对地面的压力大小为64N
D.t2=0.15πs时.箱子P对地面的压力大小为56N
3.(2025春 武汉期末)下列关于机械振动的有关说法正确的是( )
A.单摆做简谐运动的回复力是由重力和摆线拉力的合力提供
B.做简谐运动的物体,其振动能量与振动的频率有关
C.已知弹簧振子的振幅及周期,就可以确定振子在任意时刻的振动情况
D.轮船航行时,轮船摇摆的固有频率远离波浪冲击的频率,是为了防止共振
4.(2025春 武昌区期末)如图所示是某质点做简谐运动的振动图像,下列说法正确的是( )
A.质点的振幅是20cm
B.图中L点,质点的位移最小
C.图中K点,质点正在向平衡位置运动
D.质点经4s时间的路程可能小于40cm
5.(2025 盐山县三模)竖直方向振动的弹簧振子及其振动图像如图所示,已知小球质量为m=10g,弹簧的劲度系数为k=10N/m,下列说法正确的是( )
A.振子(小球)的位移随时间变化的关系式为x=5sin(πt)cm
B.在第1s末到第2s末这段时间内,小球的动能在减少、弹性势能在增加
C.小球的最大加速度为50m/s2
D.该小球在0~20s内的位移为100cm
6.(2025 贵港模拟)如图所示,物块M与m叠放在一起,以O为平衡位置,在ab之间做简谐振动,两者始终保持相对静止,取向右为正方向,其振动的位移x随时间t的变化图像如图,则下列说法正确的是( )
A.在某段时间内,两物块速度增大时,加速度可能增大,也可能减小
B.两物块运动到最大位移处时,若轻轻取走m,则M的振幅不变
C.在时间内,物块m的速度和所受摩擦力都沿负方向,且都在增大
D.从t1时刻开始计时,接下来内,两物块通过的路程为A
7.(2025 武进区校级二模)弹簧振子做简谐运动的周期公式为,其中m为振子的质量,k为弹簧的劲度系数。小鸟落在树枝上所引起树枝的振动可类比于弹簧振子的简谐运动。如图所示,两只质量不同的小鸟A和B先、后分别落在同一树枝的不同位置时,所引起树枝的振动周期恰好相同,则以下说法中正确的是( )
A.小鸟A所引起的振动的k值较小,小鸟A的质量小于小鸟B的质量
B.小鸟A所引起的振动的k值较小,小鸟A的质量大于小鸟B的质量
C.小鸟A所引起的振动的k值较大,小鸟A的质量小于小鸟B的质量
D.小鸟A所引起的振动的k值较大,小鸟A的质量大于小鸟B的质量
8.(2025春 佛山期末)如图甲所示,轻质弹簧与小球组成弹簧振子,在竖直方向上做简谐振动,其中O点为静止时小球的位置,B、C分别为最低点和最高点,取竖直向下为正方向,其振动图像如图乙所示,下列说法正确的是( )
A.小球在O点时弹簧处于原长状态
B.t=0.2s时,弹簧振子的加速度为正向最大
C.t=0.2s到t=0.4s内,弹簧振子做加速度减小的变加速直线运动
D.在t=0.1s与t=0.7s时,弹簧振子的速度大小相等、方向相反
二.多选题(共4小题)
(多选)9.(2025春 武汉期末)手机是与他人联系时使用较多的工具。手机正在充电时,闹钟响起手机振动,充电线也跟着振动,若手机振动的频率为f1,振动的充电线上某点的频率为f2,如图所示。下列说法正确的是( )
A.充电线将做受迫振动,f1=f2
B.充电线上离手机充电口近的点先振动
C.手机振动的频率越大,充电线抖动幅度越大
D.同一手机,更换不同长度充电线,振动时的频率不同
(多选)10.(2025春 天津期中)图甲为竖直方向做简谐运动的弹簧振子,小物块的质量为m,弹簧振子的振动图像如图乙所示,以向上方向为x的正方向。下列说法正确的是( )
A.t1时刻物块的速度为0
B.t2时刻弹簧的弹力为0
C.t2﹣t3时间内,物块的加速度变小
D.t3﹣t4时间内,物块的速度方向向上
(多选)11.(2025 宝丰县三模)关于做简谐运动物体的平衡位置,下列叙述正确的是( )
A.是回复力为0的位置
B.是速度为0的位置
C.是势能最大的位置
D.是回复力产生的加速度改变方向的位置
(多选)12.(2025 山东模拟)如图所示,水平地面上固定光滑斜面的倾角为30°且长度足够长,一劲度系数为k且与斜面平行的轻质弹簧下端固定在斜面底端,上端与质量为m1的小球甲相连。一条不可伸长的轻绳绕过斜面顶端的轻质光滑定滑轮,一端连接小球甲,另一端连接一轻质挂钩。开始时轻绳处于恰好伸直状态,小球甲静止在A点。现在挂钩上挂质量为m的小球乙,并将其由静止释放,当弹簧第一次恢复原长时小球甲运动到B点(图中未画出),一段时间后,小球甲到达最高点C(图中未画出)。不计一切摩擦,弹簧始终在弹性限度内,小球甲不会和定滑轮相碰,小球乙不会和地面相碰,重力加速度大小为g,小球甲、乙均可视为质点,已知弹簧弹性势能满足Epkx2(x为弹簧形变量)。下列说法正确的是( )
A.若m1=m,则BC=3AB
B.若m1=2m,则BC=2AB
C.若m1=2m,则小球甲从A点运动到C点的过程中,最大速度为
D.若m1=m,则小球甲从A点运动到C点,弹簧弹性势能的变化量为
三.填空题(共4小题)
13.(2025 福建模拟)如图甲所示,将手机挂在轻弹簧下面,并将手机向下拉一小段距离后由静止释放,手机在竖直方向做简谐运动,手机软件记录其加速度变化情况如图乙所示,以竖直向上为正方向,则在0~0.2s内,手机运动的速度 (选填“增大”或“减小”);弹簧弹力在 s(选填“0.4”或“0.8”)时刻达到最大值。
14.(2025春 泉州期中)如图所示,一质点做简谐运动,O点为平衡位置,质点从M点以速度v0向右出发,然后以v0的速度第一次通过N点,历时2s,质点通过N点后再经过1s后,第2次通过N点,在这3s内质点通过的总路程为20cm。则质点做简谐运动的振幅为 cm,周期为 s。若质点从平衡位置O点出发,则经过0.5s,通过的路程为 cm。
15.(2025春 龙岩期中)如图所示,一质点做简谐运动,先后以相同的速度依次通过M、N两点,历时1s,质点通过N点后再经过1s又再次通过N点,在这2s内质点通过的总路程为12cm。则:质点从平衡位置O到N点的时间是 s,该质点的振动周期是 s,振幅是 cm。
16.(2024秋 思明区校级期末)上课时老师将一蜂鸣器系在轻绳的一端,然后使蜂鸣器迅速水平旋转,蜂鸣器的音调竟然发生忽高忽低的变化,则旋转时蜂鸣器发声的频率 (选填“不变”或“改变”),蜂鸣器音调变低时,蜂鸣器是向 (选填“靠近”或“远离”)同学们的方向运动。
四.解答题(共4小题)
17.(2025 浦口区校级模拟)如图所示,细线上端固定于O点,下端系质量为m小球构成单摆。小球在竖直平面内做简谐运动时动能Ek随时间t的变化关系如图所示,图中坐标为已知量,重力加速度为g,求:
(1)单摆的摆长;
(2)小球最大向心加速度。
18.(2025春 佛山期末)如图所示,劲度系数k=50N/m的轻弹簧左端固定,右端与静止在光滑水平面上的小球相连,将小球向右缓慢拉至C点后由静止释放,振子(小球)在水平面上的B、C两点之间做简谐运动,O点为平衡位置,P点为OC的中点。某次振子从左向右经过OC间的P点时开始计时,t=6.0s后振子第四次返回到P点,期间通过的路程s=48cm。求:
(1)该简谐运动的周期T和振幅A;
(2)振子经过P点时回复力的大小F。
19.(2025 泗阳县校级模拟)如图所示,劲度系数为k的轻弹簧一端固定在地面,另一端与质量为m的物体P连接,跨过定滑轮的轻绳一端与物体P连接,另一端与质量为2m的物体Q连接,重力加速度为g,用手托着物体Q使轻绳刚好伸直无张力,释放后物体P做简谐运动,经过时间t物体P的速度第一次达到最大。求:
(1)物体P做简谐运动的周期和振幅(周期用含t的式子表示);
(2)物体P的最大速度;
(3)在时间t内轻绳对物体Q拉力的冲量大小。
20.(2025 盐都区校级三模)某兴趣小组研究弹簧振子,设计了如图所示的装置,一个轻弹簧竖直放置,一端固定于地面,另一端与质量为m的物体B固连在一起,整个装置被一个口径略大且足够长的光滑圆套约束(图中未画出),现将质量也为m的物体A由B的正上方某一高度处自由释放,A和B发生碰撞后两者一起以相同的速度向下运动(但不粘连),AB在以后的振动过程中恰好不会分离,弹簧的劲度系数为k,整个振动过程弹簧处于弹性限度内,忽略A、B的体积,不计空气阻力,m、k、g为已知量,求:
(1)AB一起振动过程中最大加速度的大小;
(2)小组中的甲同学通过研究弹簧弹力做功,得出了弹簧的弹性势能表达式(x为弹簧形变量),求A释放前距B的高度;
(3)已知AB一起振动的周期为T,以A与B碰撞为计时起点,求AB振动到最高点的时刻。
高考物理一轮复习 机械振动
参考答案与试题解析
一.选择题(共8小题)
1.(2025春 武汉期末)如图甲所示,把一个得筛子用四根弹簧支撑起来,筛子上装一个电动偏心轮,它每转一周,给筛子一个驱动力,这就做成了一个共振筛,该共振筛的共振曲线如图乙所示。已知增大电压,可使偏心轮转速提高;增加筛子质量,可增大筛子的固有周期。现在,在某电压下偏心轮的转速是54r/min。下列说法正确的是( )
A.共振筛现在的振动频率为0.8Hz
B.仅增加筛子质量,可以使筛子的振幅增大
C.仅减小电压,可以使筛子的振幅增大
D.现在关闭电源直到共振筛静止前,共振筛振动的周期逐渐增大
【考点】共振及其应用;阻尼振动和受迫振动.
【专题】定性思想;推理法;简谐运动专题;推理论证能力.
【答案】C
【分析】根据振动周期和频率关系列式,结合共振曲线进行分析解答。
【解答】解:A.共振筛现在的振动周期为Ts≈1.11s,则振动频率为f,解得f=0.9Hz,故A错误;
BC.由图乙可知,筛子固有频率为0.8Hz,减小电压会降低偏心轮转速,偏心轮的频率减小,则筛子固有频率和驱动力频率的差值变小,筛子振幅增大,增加筛子质量,筛子的固有周期增大,则固有频率减小,则固有频率和驱动力频率的差值变大,筛子振幅减小,故B错误,C正确;
D.关闭电源后共振筛自由振动,直到共振筛静止前,共振筛振动的周期不变,故D错误。
故选:C。
【点评】考查振动周期和频率关系列式,共振曲线的理解,会根据题意进行准确分析解答。
2.(2025 临汾模拟)如图甲所示,质量M=5.0kg的箱子P放在水平地面上,两根相同的轻质弹簧连着质量m=1.0kg的小球Q,两弹簧另一端与箱子P连接,弹簧均处于竖直状态。取竖直向上为正方向,小球在竖直方向振动过程中相对平衡位置的位移y随时间t的变化如图乙所示,箱子P始终保持静止。已知两弹簧的劲度系数k=50N/m,重力加速度g=10m/s2,则( )
A.t1=0.05πs时,小球的加速度为零
B.t=0.1πs时.小球的速度为零
C.t2=0.15πs时,箱子P对地面的压力大小为64N
D.t2=0.15πs时.箱子P对地面的压力大小为56N
【考点】简谐运动的图像问题.
【专题】定量思想;推理法;振动图象与波动图象专题;推理论证能力.
【答案】C
【分析】回复力最大,加速度为最大;
平衡位置处,速度为最大;
根据平衡条件列式,求x,t2=0.15πs时刻,偏离平衡位置的位移为A,根据平衡条件结合牛顿第三定律,求箱子对地面的压力。
【解答】解:A.t1=0.05πs时刻小球在正向最大位移处,回复力最大,由牛顿第二定律,加速度为最大,故A错误;
B.t=0.1πs时刻小球在平衡位置处,速度为最大,故B错误;
CD.两弹簧相同,Q静止时,上方弹簧伸长,下方弹簧压缩,设弹簧形变量为x,根据平衡条件有2kx=m2g
解得x=0.1m
由图乙知t2=0.15πs时刻小球在最低点,偏离平衡位置的位移为A,此时上方弹簧拉伸到更长,下方弹簧压缩到更短,根据平衡条件,对箱子有FN=Mg+2k(A+x),代入数据解得FN=64N
由牛顿第三定律知箱子对地面的压力为64N,故C正确,D错误。
故选:C。
【点评】本题解题关键要掌握不同位置的速度加速度位移特征,位移为零时,加速度最小速度最大,位移最大时加速度最大速度最小。
3.(2025春 武汉期末)下列关于机械振动的有关说法正确的是( )
A.单摆做简谐运动的回复力是由重力和摆线拉力的合力提供
B.做简谐运动的物体,其振动能量与振动的频率有关
C.已知弹簧振子的振幅及周期,就可以确定振子在任意时刻的振动情况
D.轮船航行时,轮船摇摆的固有频率远离波浪冲击的频率,是为了防止共振
【考点】共振及其应用;简谐运动的定义、运动特点与判断;单摆及单摆的条件.
【专题】定性思想;推理法;单摆问题;推理论证能力.
【答案】D
【分析】根据回复力、振幅以及振动方程和共振的防止和利用进行分析解答。
【解答】解:A.单摆做简谐运动的回复力是由重力沿切线方向的分力提供,故A错误;
B.做简谐运动的物体,其振动能量与振动的振幅有关,故B错误;
C.已知弹簧振子的振幅及周期,并不能确定振子在任意时刻的振动情况,必须利用振动方程才能确定,故C错误;
D.轮船航行时,轮船摇摆的固有频率远离波浪冲击的频率,是为了防止共振,故D正确。
故选:D。
【点评】考查回复力、振幅以及振动方程和共振的防止和利用,会根据题意进行准确分析解答。
4.(2025春 武昌区期末)如图所示是某质点做简谐运动的振动图像,下列说法正确的是( )
A.质点的振幅是20cm
B.图中L点,质点的位移最小
C.图中K点,质点正在向平衡位置运动
D.质点经4s时间的路程可能小于40cm
【考点】简谐运动的图像问题.
【专题】定性思想;推理法;振动图象与波动图象专题;理解能力.
【答案】C
【分析】根据图像可知振幅、L的位置和M的振动方向;质点经一个周期通过的路程为4A。
【解答】解:A、根据图像可知,质点的振幅是10cm,故A错误;
B、图中L点处于波谷,质点的位移最大,故B错误;
C、有图可知,图中K点,质点正在向平衡位置运动,故C正确;
D、质点经4s时间(即一个周期)通过的路程为:s=4A=4×10cm=40cm,故D错误。
故选:C。
【点评】本题主要是考查了振动的图像;解答此类问题的关键是要理解振动图像的物理意义,能够根据图像直接读出振幅和质点的振动方向。
5.(2025 盐山县三模)竖直方向振动的弹簧振子及其振动图像如图所示,已知小球质量为m=10g,弹簧的劲度系数为k=10N/m,下列说法正确的是( )
A.振子(小球)的位移随时间变化的关系式为x=5sin(πt)cm
B.在第1s末到第2s末这段时间内,小球的动能在减少、弹性势能在增加
C.小球的最大加速度为50m/s2
D.该小球在0~20s内的位移为100cm
【考点】简谐运动的回复力;简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定量思想;归纳法;简谐运动专题;分析综合能力.
【答案】C
【分析】根据图像得到振幅和周期,然后求出角速度,便可得到位移随时间变化的关系式;简谐运动过程中动能和势能相互转化,可根据图像确定转化情况;根据F=kA求出最大弹力,根据牛顿第二定律可求出小球的最大加速度;首先求出20s为多少周期,再求位移。
【解答】解:A.由图可知,小球振动的周期T为4s,振幅A为5cm,则小球的位移随时间变化的关系式为
故A错误;
B.小球在最大位移处速度为零,弹簧弹性势能最大,所以在第1s末到第2s末这段时间内,小球从最大位移运动到平衡位置,则小球的动能在增加、弹性势能在减小,故B错误;
C.小球在最大位移处时受到的弹力最大为
F=kA=10N/m×5×10﹣2m=0.5N
则根据牛顿第二定律可得,小球的最大加速度为
故C正确;
D.由图可知,小球周期为4s,20s即为4个周期,所以该小球在0~20s内的位移为零,故D错误。
故选:C。
【点评】本题关键是可以从简谐运动图像中获取基本信息,然后结合简谐运动的周期性及牛顿第二定律求解即可。
6.(2025 贵港模拟)如图所示,物块M与m叠放在一起,以O为平衡位置,在ab之间做简谐振动,两者始终保持相对静止,取向右为正方向,其振动的位移x随时间t的变化图像如图,则下列说法正确的是( )
A.在某段时间内,两物块速度增大时,加速度可能增大,也可能减小
B.两物块运动到最大位移处时,若轻轻取走m,则M的振幅不变
C.在时间内,物块m的速度和所受摩擦力都沿负方向,且都在增大
D.从t1时刻开始计时,接下来内,两物块通过的路程为A
【考点】简谐运动过程中速度、加速度(回复力)与位移的变化问题;简谐运动的某一时刻或某段时间内质点的运动情况;简谐运动的图像问题.
【专题】定性思想;推理法;振动图象与波动图象专题;推理论证能力.
【答案】B
【分析】在最大位移处,加速度最大,静摩擦力最大。由图像可读出振子振动的周期和振幅,振子向平衡位置运动的过程中,速度增大,加速度减小。通过分析振子位移的变化,即可判断其速度和加速度的变化。
【解答】解:A.物块速度增大时,物块向平衡位置运动,则物块的位移减小,据简谐振动的受力特点F=﹣kx,加速度减小,故A错误;
B.简谐运动是一种无能量损失的振动,它只是动能和势能间的转化,总机械能守恒。其能量只有振幅决定,即振幅不变,振动系统能量不变。当将m在最大位移处轻轻取走,说明m取走时动能为零,m取走前后M振幅没有改变,振动系统机械能总量不变,故B正确。
C.由物体振动的位移x随时间t的变化图像可知在时间内,由图像的斜率为负且增大可知,物块m的速度沿负方向在增大,受摩擦力方向沿负方向,据F=﹣kx可知,位移x在减小,回复力减小,加速度在减小,所以摩擦力在减小,故C错误;
D.由振动的位移x随时间t的变化图像知,两物块在平衡位置速度最大,因此两物块从b→O的平均速率要小于从t1开始经时间内的平均速率,所以从t1开始经通过的路程大于A,故D错误。
故选:B。
【点评】解答该题的关键是弄清m的恢复力的来源以及注意最大位移处将一质量为m的物块轻轻地拿走表示的是小物块拿走时水平方向的速度为0,此时无机械能损失。
7.(2025 武进区校级二模)弹簧振子做简谐运动的周期公式为,其中m为振子的质量,k为弹簧的劲度系数。小鸟落在树枝上所引起树枝的振动可类比于弹簧振子的简谐运动。如图所示,两只质量不同的小鸟A和B先、后分别落在同一树枝的不同位置时,所引起树枝的振动周期恰好相同,则以下说法中正确的是( )
A.小鸟A所引起的振动的k值较小,小鸟A的质量小于小鸟B的质量
B.小鸟A所引起的振动的k值较小,小鸟A的质量大于小鸟B的质量
C.小鸟A所引起的振动的k值较大,小鸟A的质量小于小鸟B的质量
D.小鸟A所引起的振动的k值较大,小鸟A的质量大于小鸟B的质量
【考点】简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定性思想;归纳法;简谐运动专题;理解能力.
【答案】A
【分析】根据弹簧振子做简谐运动的周期公式分析即可。
【解答】解:两小鸟引起振动的周期相同,但枝头处的k相对较小,根据简谐运动的周期公式可知,枝头处小鸟的质量较小,故A正确,BCD错误。
故选:A。
【点评】知道枝头处的k相对较小是解题的关键。
8.(2025春 佛山期末)如图甲所示,轻质弹簧与小球组成弹簧振子,在竖直方向上做简谐振动,其中O点为静止时小球的位置,B、C分别为最低点和最高点,取竖直向下为正方向,其振动图像如图乙所示,下列说法正确的是( )
A.小球在O点时弹簧处于原长状态
B.t=0.2s时,弹簧振子的加速度为正向最大
C.t=0.2s到t=0.4s内,弹簧振子做加速度减小的变加速直线运动
D.在t=0.1s与t=0.7s时,弹簧振子的速度大小相等、方向相反
【考点】简谐运动的图像问题;简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定性思想;推理法;简谐运动专题;理解能力.
【答案】C
【分析】根据弹簧振子振动特点结合振动图像进行逐项分析。
【解答】解:A、O点为静止时小球的位置,小球在O点时弹簧处于伸长状态,故A错误;
B、t=0.2s时,弹簧振子处于下方振幅处,根据a可知,加速度为负向最大,故B错误;
C、t=0.2s到t=0.4s内,弹簧振子的位移减小、速度最大、加速度减小,所以,振子做加速度减小的变加速直线运动,故C正确;
D、根据图乙可知,在t=0.1s与t=0.7s时,弹簧振子的速度大小相等、方向相同,故D错误。
故选:C。
【点评】本题主要是考查了简谐运动的知识;知道简谐运动的平衡位置是物体静止时受力平衡的位置;振动的质点在振动过程中各物理量的变化情况可以这样分析:位移增大→回复力增大→加速度增大→速度减小→动能减小→势能增大。
二.多选题(共4小题)
(多选)9.(2025春 武汉期末)手机是与他人联系时使用较多的工具。手机正在充电时,闹钟响起手机振动,充电线也跟着振动,若手机振动的频率为f1,振动的充电线上某点的频率为f2,如图所示。下列说法正确的是( )
A.充电线将做受迫振动,f1=f2
B.充电线上离手机充电口近的点先振动
C.手机振动的频率越大,充电线抖动幅度越大
D.同一手机,更换不同长度充电线,振动时的频率不同
【考点】共振及其应用.
【专题】定性思想;推理法;简谐运动专题;推理论证能力.
【答案】AB
【分析】根据受迫振动和共振的特点进行分析解答。
【解答】解:AD.共振闹钟响起手机振动,充电线也跟着振动,可知充电线做受迫振动,则有f1=f2,由于受迫振动的频率取决于驱动力的频率,所以同一手机,更换不同长度充电线,振动时的频率相同,故A正确,D错误。
B.充电线上越靠近振源位置的点越先振动,所以充电线上离手机充电口近的点先振动,故B正确;
C.当手机振动的频率等于充电线振动的固有频率时,充电线抖动幅度最大,所以手机振动的频率越大,充电线抖动幅度不一定越大,故C错误。
故选:AB。
【点评】考查受迫振动和共振的特点,会根据题意进行准确分析解答。
(多选)10.(2025春 天津期中)图甲为竖直方向做简谐运动的弹簧振子,小物块的质量为m,弹簧振子的振动图像如图乙所示,以向上方向为x的正方向。下列说法正确的是( )
A.t1时刻物块的速度为0
B.t2时刻弹簧的弹力为0
C.t2﹣t3时间内,物块的加速度变小
D.t3﹣t4时间内,物块的速度方向向上
【考点】简谐运动的表达式及振幅、周期、频率、相位等参数;简谐运动的回复力.
【专题】定性思想;推理法;简谐运动专题;推理论证能力.
【答案】AD
【分析】根据位移图像的斜率等于速度,分析速度的大小和方向;根据图像读出位移,进而分析振子的加速度大小及方向。
【解答】解:A、由图像可知,t1时刻物块处于最大位移处,则速度为零,故A正确;
B、t2时刻物块在平衡位置处,回复力等于零,所以此时弹簧的弹力等于物块的重力,故B错误;
C、由图可知t3时刻物块处于负向的最大位移处,所以在t2﹣t3时间内,物块由平衡位置向下运动到负向的最大位移处,位移逐渐增大,则加速度逐渐增大,故C错误;
D、t3时刻物块处于负向的最大位移处,所以在t3﹣t4时间内,物块由负向的最大位移处运动到平衡位置处,速度向上,故D正确。
故选:AD。
【点评】解决该题需熟练掌握简谐运动的运动过程,会根据振动图像判断位移和速度的变化情况。
(多选)11.(2025 宝丰县三模)关于做简谐运动物体的平衡位置,下列叙述正确的是( )
A.是回复力为0的位置
B.是速度为0的位置
C.是势能最大的位置
D.是回复力产生的加速度改变方向的位置
【考点】简谐运动的回复力;简谐运动的定义、运动特点与判断.
【专题】定性思想;推理法;简谐运动专题;理解能力;推理论证能力.
【答案】AD
【分析】做简谐运动物体的回复力F=﹣kx,x表示物体偏离平衡位置的距离,平衡位置处物体的加速度为零,速度最大,势能最小。
【解答】解:A、做简谐运动物体的回复力F=﹣kx,x表示物体偏离平衡位置的距离,物体在平衡位置时,x=0,所以平衡位置是回复力为零的位置,故A正确,
BC、平衡位置物体的加速度为零,速度最大,势能最小,故BC错误,
D、平衡位置处物体的加速度为零,该位置为回复力产生加速度方向改变的位置,故D正确,
故选:AD。
【点评】本题考查平衡位置的理解,注意概念的学习。
(多选)12.(2025 山东模拟)如图所示,水平地面上固定光滑斜面的倾角为30°且长度足够长,一劲度系数为k且与斜面平行的轻质弹簧下端固定在斜面底端,上端与质量为m1的小球甲相连。一条不可伸长的轻绳绕过斜面顶端的轻质光滑定滑轮,一端连接小球甲,另一端连接一轻质挂钩。开始时轻绳处于恰好伸直状态,小球甲静止在A点。现在挂钩上挂质量为m的小球乙,并将其由静止释放,当弹簧第一次恢复原长时小球甲运动到B点(图中未画出),一段时间后,小球甲到达最高点C(图中未画出)。不计一切摩擦,弹簧始终在弹性限度内,小球甲不会和定滑轮相碰,小球乙不会和地面相碰,重力加速度大小为g,小球甲、乙均可视为质点,已知弹簧弹性势能满足Epkx2(x为弹簧形变量)。下列说法正确的是( )
A.若m1=m,则BC=3AB
B.若m1=2m,则BC=2AB
C.若m1=2m,则小球甲从A点运动到C点的过程中,最大速度为
D.若m1=m,则小球甲从A点运动到C点,弹簧弹性势能的变化量为
【考点】简谐运动的能量问题;简谐运动过程中速度、加速度(回复力)与位移的变化问题;简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定量思想;方程法;简谐运动专题;机械能守恒定律应用专题;推理论证能力.
【答案】AC
【分析】根据受力平衡求出开始时弹簧的压缩量和平衡位置处弹簧的压缩量,然后结合简谐振动的对称性分析BC与AB的关系;当小球受到的合外力等于零时,小球的速度最大,由此结合弹簧弹性势能的公式求出;根据机械能守恒求出。
【解答】解:甲、乙两球与弹簧构成的系统机械能守恒,可知甲、乙两球的运动是简谐运动,没有悬挂小球乙时,弹簧处于压缩状态,对小球甲有m1gsin 30°=kx1
解得x1
根据简谐运动的特征,小球甲运动到平衡位置O点时所受合力为零,有mg=m1gsin 30°+kx2
解得x2
A、若m1=m,则小球甲运动到平衡位置O点时有x2=x1,弹簧处于拉伸状态,可知平衡位置O点在弹簧原长B位置的上方,根据简谐运动的对称性规律可知AO=AB+BO=x1+x2=OC,如图
则BC=BO+OC=x1+2x23AB,故A正确;
B、若m1=2m,小球甲运动到平衡位置O点时x'2=0,弹簧处于原长,可知平衡位置O点在弹簧原长B位置处,根据简谐运动的对称性规律可知 AO=AB=OC,则BC=AB,故B错误;
C、若m1=2m,小球甲从A 点运动到C点的过程中,小球甲运动到平衡位置O点时速度最大,小球甲从A点运动到O点弹簧的形变量从x1变为x'2=0,弹性势能减小,根据能量守恒定律有ΔE'p+mgx1(2m+m)2mgx1sin 30°
其中ΔE'pk
解得vm,故C正确。
D、若m1=m,小球甲从A点运动到C点,根据能量守恒定律有ΔEp=mg 2(x1+x2)﹣mg 2(x1+x2)sin 30°
解得ΔEp,故D错误;
故选:AC。
【点评】对于简谐振动的问题,抓住简谐振动的对称性,以及正确判断平衡位置是关键。
三.填空题(共4小题)
13.(2025 福建模拟)如图甲所示,将手机挂在轻弹簧下面,并将手机向下拉一小段距离后由静止释放,手机在竖直方向做简谐运动,手机软件记录其加速度变化情况如图乙所示,以竖直向上为正方向,则在0~0.2s内,手机运动的速度 增大 (选填“增大”或“减小”);弹簧弹力在 0.8 s(选填“0.4”或“0.8”)时刻达到最大值。
【考点】简谐运动过程中速度、加速度(回复力)与位移的变化问题;简谐运动的回复力.
【专题】定量思想;方程法;简谐运动专题;推理论证能力.
【答案】增大;0.8。
【分析】根据做简谐运动的物体远离平衡位置,加速度越大,速度越小分析;由受力分析和牛顿第二定律可知弹簧弹力大小。
【解答】解:从t=0至t=0.2s过程,手机的加速度减小,可知手机从最大位移处向平衡位置运动,手机的速度增大。
根据a,结合以竖直向上为正方向可知,在t=0.8s时刻手机位于最高点,弹簧的弹力与重力的和提供向心力,即kA=mg+kx;而t=0.8s时刻手机位于最低点,弹簧弹力减去重力的差提供向心力,即kA=kx′﹣mg,对比可知在t=0.8s时刻弹簧的弹力达到最大。
故答案为:增大;0.8。
【点评】本题考查了简谐运动的图像问题、简谐运动的特点,解题的关键是知道简谐运动加速度方向始终指向平衡位置,加速度方向与相对平衡位置的位移的方向始终相反。
14.(2025春 泉州期中)如图所示,一质点做简谐运动,O点为平衡位置,质点从M点以速度v0向右出发,然后以v0的速度第一次通过N点,历时2s,质点通过N点后再经过1s后,第2次通过N点,在这3s内质点通过的总路程为20cm。则质点做简谐运动的振幅为 10 cm,周期为 6 s。若质点从平衡位置O点出发,则经过0.5s,通过的路程为 5 cm。
【考点】简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定量思想;方程法;简谐运动专题;推理论证能力.
【答案】10;6;5。
【分析】简谐运动的质点,先后以同样大小的速度通过M、N两点,则可判定这两点关于平衡位置对称,根据对称性可求解;根据振动方程求解。
【解答】解:质点先后以相同的速度依次通过M、N两点,可知M、N两点关于平衡位置O点对称,所以质点由M到O时间与由O到N的时间相等,则质点从平衡位置O到N点的时间t1=1s
因过N点后再经过1s质点以方向相反、大小相同的速度再次通过N点,则有从N点到最大位置的时间t2=0.5s
因此,质点振动的周期是T=4×(t1+t2)
代入数据得T=6s
3s为半个周期,质点在半个周期内总路程等于2倍振幅,所以振幅Acm=10cm
质点从平衡位置O点出发,则经过0.5s,则质点的位移x=Asin()=10×sin()cm=5cm
可知在这0.5s时间内质点的路程也是5cm
故答案为:质点从平衡位置O点出发,则经过0.5s,
【点评】本题考查简谐运动的相关问题,考查知识点针对性强,难度较小,考查了学生掌握知识与应用知识的能力。
15.(2025春 龙岩期中)如图所示,一质点做简谐运动,先后以相同的速度依次通过M、N两点,历时1s,质点通过N点后再经过1s又再次通过N点,在这2s内质点通过的总路程为12cm。则:质点从平衡位置O到N点的时间是 0.5 s,该质点的振动周期是 4 s,振幅是 6 cm。
【考点】简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定量思想;方程法;简谐运动专题;推理论证能力.
【答案】0.5,4,6。
【分析】简谐运动的质点,先后以同样大小的速度通过M、N两点,则可判定这两点关于平衡位置对称,根据对称性可求解。
【解答】解:质点做简谐运动,先后以相同的速度依次通过M、N两点,历时1s,过N点后再经过t=1s质点以方向相反、大小相同的速度再次通过N点,可知开始时质点运动的方向向右;质点先后以相同的速度依次通过M、N两点,可知M、N两点关于平衡位置O点对称,所以质点由M到O点的时间与由O到N的时间相等,那么平衡位置O到N点的时间t1=0.5s。因过N点后再经过t=1s质点以方向相反、大小相同的速度再次通过N点,则质点从N点到最大位置的时间t2=0.5s;因此质点振动的周期是T=4×(t1+t2),代入数据得T=4s;
结合以上的分析,可知质点从M到N,然后以相反的方向再到N恰好经过了半个周期,则质点总路程的一半,即为振幅,所以振幅Acm=6cm。
故答案为:0.5,4,6。
【点评】本题考查简谐运动的相关问题,考查知识点针对性强,难度较小,考查了学生掌握知识与应用知识的能力。
16.(2024秋 思明区校级期末)上课时老师将一蜂鸣器系在轻绳的一端,然后使蜂鸣器迅速水平旋转,蜂鸣器的音调竟然发生忽高忽低的变化,则旋转时蜂鸣器发声的频率 不变 (选填“不变”或“改变”),蜂鸣器音调变低时,蜂鸣器是向 远离 (选填“靠近”或“远离”)同学们的方向运动。
【考点】共振及其应用.
【专题】定性思想;推理法;波的多解性;推理论证能力.
【答案】不变;远离。
【分析】振源与观察者之间存在着相对运动,使观察者听到的声音频率不同于振源频率的现象,这就是频移现象。因为,声源相对于观测者在运动时,观测者所听到的声音会发生变化,当声源离观测者而去时,声波的波长增加,音调变得低沉,当声源接近观测者时,声波的波长减小,音调就变高。
【解答】解:旋转时蜂鸣器发声的频率不变。根据多普勒效应,当蜂鸣器向远离同学们的方向运动时,同学们听到声音的频率变小,即音调变低。
故答案为:不变;远离。
【点评】本题考查多普勒效应,知道在波源与观察者靠近时,观察者接收到的波的频率变高,而在波源与观察者远离时接收的频率变低,即高亢表示远离,低沉表示靠近。
四.解答题(共4小题)
17.(2025 浦口区校级模拟)如图所示,细线上端固定于O点,下端系质量为m小球构成单摆。小球在竖直平面内做简谐运动时动能Ek随时间t的变化关系如图所示,图中坐标为已知量,重力加速度为g,求:
(1)单摆的摆长;
(2)小球最大向心加速度。
【考点】单摆的能量转化;向心加速度的表达式及影响向心加速度大小的因素.
【专题】计算题;学科综合题;定量思想;方程法;单摆问题;推理论证能力.
【答案】(1)单摆的摆长为;
(2)小球最大向心加速度为。
【分析】(1)根据题图解得周期,结合周期公式解得摆长;
(2)根据向心加速度的公式解答。
【解答】解:(1)摆球一个周期内两次经过最低点,则一个周期内两次动能最大,由图可知,单摆的周期T=4t0
根据单摆周期公式
解得
(2)摆球到最低点的动能
速度最大时对应向心加速度的最大值
得
答:(1)单摆的摆长为;
(2)小球最大向心加速度为。
【点评】本题考查单摆周期公式的应用,解题关键掌握单摆的周期公式的运用。
18.(2025春 佛山期末)如图所示,劲度系数k=50N/m的轻弹簧左端固定,右端与静止在光滑水平面上的小球相连,将小球向右缓慢拉至C点后由静止释放,振子(小球)在水平面上的B、C两点之间做简谐运动,O点为平衡位置,P点为OC的中点。某次振子从左向右经过OC间的P点时开始计时,t=6.0s后振子第四次返回到P点,期间通过的路程s=48cm。求:
(1)该简谐运动的周期T和振幅A;
(2)振子经过P点时回复力的大小F。
【考点】简谐运动的回复力;简谐运动的表达式及振幅、周期、频率、相位等参数.
【专题】定量思想;方程法;简谐运动专题;理解能力.
【答案】(1)该简谐运动的周期为3s和振幅6cm;
(2)振子经过P点时回复力的大小1.5N。
【分析】通过给定的时间和振子返回特定点的次数来确定简谐运动的周期。
利用振子在特定时间内通过的总路程来计算振幅。
根据振子在P点的位置,利用回复力的定义计算回复力的大小。
【解答】解:(1)根据题意有
t=2T
解得
T=3s
根据题意有
s=8A
解得
A=6cm
(2)振子经过P点时偏离平衡位置O的位移大小
根据回复力公式有
F=kx
解得
F=1.5N
答:(1)该简谐运动的周期为3s和振幅6cm;
(2)振子经过P点时回复力的大小1.5N。
【点评】此题考查了简谐运动的基本概念,包括周期、振幅的计算以及回复力的计算。
19.(2025 泗阳县校级模拟)如图所示,劲度系数为k的轻弹簧一端固定在地面,另一端与质量为m的物体P连接,跨过定滑轮的轻绳一端与物体P连接,另一端与质量为2m的物体Q连接,重力加速度为g,用手托着物体Q使轻绳刚好伸直无张力,释放后物体P做简谐运动,经过时间t物体P的速度第一次达到最大。求:
(1)物体P做简谐运动的周期和振幅(周期用含t的式子表示);
(2)物体P的最大速度;
(3)在时间t内轻绳对物体Q拉力的冲量大小。
【考点】简谐运动的表达式及振幅、周期、频率、相位等参数;弹簧类问题中的机械能守恒;动量定理的内容和应用.
【专题】定量思想;推理法;机械能守恒定律应用专题;动量定理应用专题;推理论证能力.
【答案】(1)物体P做简谐运动的周期为4t,振幅为;
(2)物体P的最大速度为;
(3)在时间t内轻绳对物体Q拉力的冲量大小为。
【分析】(1)从速度为0到第一次达到最大经过的时间是,求周期,根据弹力和重力平衡列式,求压缩量x1,当物体P的速度最大时加速度为0,合力为零,根据平衡列式,求伸长量x2,确定振幅;
(2)根据系统的机械能守恒列式,求速度;
(3)根据动量定理,求在时间t内轻绳对物体Q拉力的冲量大小。
【解答】解:(1)对物体P分析,从速度为0到第一次达到最大经过的时间是,则有
解得
T=4t
物体P从速度为0到第一次达到最大走过的位移大小是A,A是振幅,设刚释放时弹簧的压缩量为x1,弹力和重力平衡,则有
kx1=mg
解得
当物体P的速度最大时加速度为0,合力为零,设此时弹簧的伸长量为x2,根据平衡列式则有
kx2+mg=2mg
解得
振幅
(2)从释放到物体P速度首次达到最大,弹簧开始的压缩量和最后的伸长量相等,弹簧弹性势能相等,设最大速度为v,根据系统的机械能守恒得
代入得
(3)设在时间t内轻绳对物体Q拉力的冲量大小为I,以向下为正方向,根据动量定理得
2mgt﹣I=2mv
代入得
答:(1)物体P做简谐运动的周期为4t,振幅为;
(2)物体P的最大速度为;
(3)在时间t内轻绳对物体Q拉力的冲量大小为。
【点评】本题解题关键是掌握系统的机械能守恒定律、动量定理等,具有一定综合性,难度中等。
20.(2025 盐都区校级三模)某兴趣小组研究弹簧振子,设计了如图所示的装置,一个轻弹簧竖直放置,一端固定于地面,另一端与质量为m的物体B固连在一起,整个装置被一个口径略大且足够长的光滑圆套约束(图中未画出),现将质量也为m的物体A由B的正上方某一高度处自由释放,A和B发生碰撞后两者一起以相同的速度向下运动(但不粘连),AB在以后的振动过程中恰好不会分离,弹簧的劲度系数为k,整个振动过程弹簧处于弹性限度内,忽略A、B的体积,不计空气阻力,m、k、g为已知量,求:
(1)AB一起振动过程中最大加速度的大小;
(2)小组中的甲同学通过研究弹簧弹力做功,得出了弹簧的弹性势能表达式(x为弹簧形变量),求A释放前距B的高度;
(3)已知AB一起振动的周期为T,以A与B碰撞为计时起点,求AB振动到最高点的时刻。
【考点】简谐运动的某一时刻或某段时间内质点的运动情况;牛顿第二定律的简单应用;动量守恒与能量守恒共同解决实际问题.
【专题】定量思想;推理法;振动图象与波动图象专题;机械能守恒定律应用专题;推理论证能力.
【答案】(1)AB一起振动过程中最大加速度的大小为g;
(2)A释放前距B的高度为;
(3)AB振动到最高点的时刻为。
【分析】(1)根据牛顿第二定律,求加速度最大值;
(2)根据受力平衡列式,结合机械能守恒和碰撞过程的动量守恒,求h。
(3)确定振幅,写振动方程,根据AB碰撞位置,求时间,确定AB振动到最高点的时刻。
【解答】解:(1)AB在以后的振动过程中恰好不会分离,所以振动最高点为弹簧原长位置,此时加速度最大.根据牛顿第二定律有2mg=2ma
解得a=g
(2)B静止时,根据受力平衡有kx0=mg
物体A自由下落的过程,由机械能守恒得
物体A、B碰撞过程,根据动量守恒有mv0=2mv
碰后AB在以后振动过程中到达最高点时弹簧刚好处于原长状态,相对于原来向上运动得距离
对物体A、B和弹簧组成的系统,由能量守恒得
联立解得
(3)在振动过程中,设平衡位置弹簧的压缩量为x,有2mg=kx
振幅
以第一次向下经过平衡位置为0时刻,取向下为正方向,则振动方程为y=Asinωt
AB碰撞时y1=Asinωt1=x﹣x0
解得
因此以A与B碰撞为时起点,求AB振动到最高点的时刻
答:(1)AB一起振动过程中最大加速度的大小为g;
(2)A释放前距B的高度为;
(3)AB振动到最高点的时刻为。
【点评】本题解题关键是掌握受力平衡、碰撞中的动量守恒,系统的能量转化和守恒规律,能够正确书写振动方程,根据位置,确定时刻,难度中等。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
