通用版四年级奥数培优测试卷(含答案)
文档属性
| 名称 | 通用版四年级奥数培优测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 196.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 08:42:30 | ||
图片预览



文档简介
四年级奥数培优测试卷
1. 计算:1 2+3 4+ 98+99=( )。
A.50 B.49 C.48 D.45
2.计算:2024÷(20+24)-2025÷(20+25)=( )。
A.1 B.2 C.3 D.4
3.1949年,我国一年全国用电总量仅43亿千瓦时,人口总量约5.42亿人。而75年后的今天,我国全年用电总量达到了92241亿千瓦时,人口总量约14.1亿人,发电量增长超2000倍。在今天,我国每人每天平均用电量大约是75年前每人约( )天的用电量。
A. 640 B. 800 C. 1200 D. 1800
4.计算 =( )。
A. 1234567891011121314151617181716151413121110987654321
B. 12345679012345678987654320987654321
C. 123456789012345678987654320987654321
D. 123456790123456789876543210987654321
5.小可午饭时选择了一份可自行搭配的套餐,其中主菜有6种,可任选其中一种;配菜有4种,可任选其中一种;甜品有2种,可任选其中一种也可不选。小可的午饭共有( )种搭配方案。
A. 72 B.60 C. 48 D. 36
6.下图是A,B,C,D 四个货场之间的道路示意图,□中的数是各货场储存的货物重量(单位:吨),道路上标注的数表示两货场之间的距离(单位:千米)。现在要把全部的货物集中到其中的一个货场中,如果每吨货物运输1千米需要付5元运输费,那么总运输费最少是( )元。
A.3264 B.4464 C.16320 D.22320
7.阿呆和阿瓜各有一些藏书,如果阿瓜送给阿呆20本书,那么阿呆的藏书数量就是阿瓜的7倍;如果阿呆送给阿瓜20本书,那么阿呆的藏书数量就是阿瓜的3倍。原来阿呆的藏书有( )本。
A.220 B. 240 C. 260 D.280
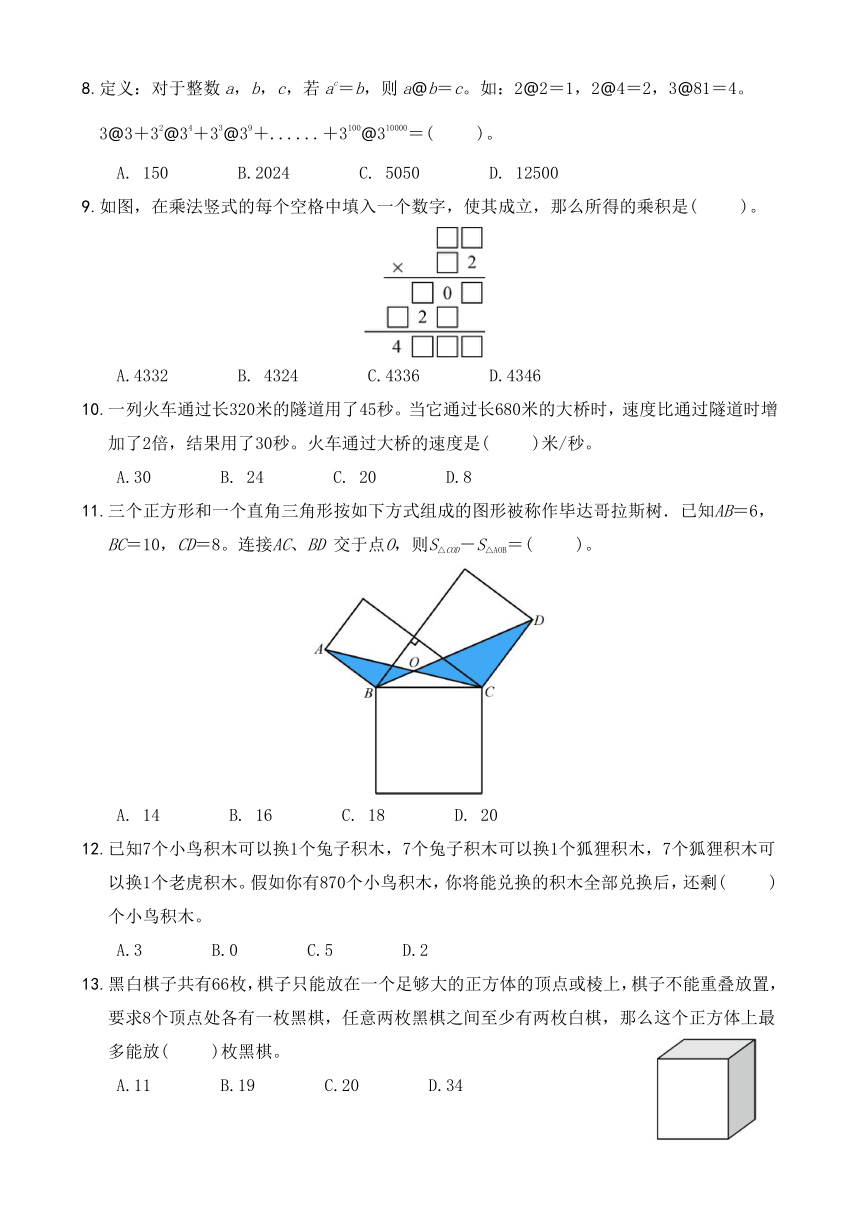
8.定义:对于整数a,b,c,若ac=b,则a@b=c。如:2@2=1,2@4=2,3@81=4。
3@3+32@34+33@39+......+3100@310000=( )。
A. 150 B.2024 C. 5050 D. 12500
9.如图,在乘法竖式的每个空格中填入一个数字,使其成立,那么所得的乘积是( )。
A.4332 B. 4324 C.4336 D.4346
10.一列火车通过长320米的隧道用了45秒。当它通过长680米的大桥时,速度比通过隧道时增加了2倍,结果用了30秒。火车通过大桥的速度是( )米/秒。
A.30 B. 24 C. 20 D.8
11.三个正方形和一个直角三角形按如下方式组成的图形被称作毕达哥拉斯树.已知AB=6,BC=10,CD=8。连接AC、BD 交于点O,则S△COD-S△AOB=( )。
A. 14 B. 16 C. 18 D. 20
12.已知7个小鸟积木可以换1个兔子积木,7个兔子积木可以换1个狐狸积木,7个狐狸积木可以换1个老虎积木。假如你有870个小鸟积木,你将能兑换的积木全部兑换后,还剩( )个小鸟积木。
A.3 B.0 C.5 D.2
13.黑白棋子共有66枚,棋子只能放在一个足够大的正方体的顶点或棱上,棋子不能重叠放置,要求8个顶点处各有一枚黑棋,任意两枚黑棋之间至少有两枚白棋,那么这个正方体上最多能放( )枚黑棋。
A.11 B.19 C.20 D.34
14.近些年电竞比赛中有一个非常流行的赛制叫瑞士轮,它指的是随机公平地编排第一轮比赛(一般由抽签决定),接着开始比赛。当某一轮比赛结束后,可以得到所有比赛选手的总积分(常见表达为胜场数—负场数,例如某个队伍2胜1负可以表示为2—1)。根据这个总积分的高低,把比赛选手由高到低排序(总积分相同则并列随机排序),接着是第1名对第2名,第3名对第4名,…,任何两队不重复对抗(若有两队之前比赛过,则微调排序使他们的对手都是之前没有比赛过的),如此循环,直到所有轮次结束。现在有16个队伍参加比赛,资格赛阶段采用单场定胜负的瑞士轮赛制,规定先达到3 胜场晋级,先达到3 负场淘汰,那么资格赛阶段共( )场比赛。
A.36 B.32 C.20 D.33
15.唐僧师徒四人来到一片桃园摘桃充饥,唐僧吃了2个桃子,猪八戒吃的桃子数量是沙和尚的5 倍,沙和尚吃的桃子数量是孙悟空的一半。这时突然遭遇妖怪,降妖除魔后,每人又吃了一些桃子补充体力,这次他们吃的都一样多。最终发现四人前前后后一共在桃园吃了42个桃子,其中孙悟空吃了( )个桃子。
A.6 B.8 C.9 D.10
16.有一些数字饼干按照如下规律排列成一个多位数:199019911992…2025,贪吃虫吃掉其中的100 块饼干后(不能改变饼干的顺序),剩下的多位数最小,那么这个多位数的数字之和是( )。
A.4 B.6 C.8 D.10
17.MathClub举办800米接力赛,有两个队参加比赛,每个队各有6人。各个队按照自己的打算将全程分成6段(每一段的长度不一定相等),每个队员以恒定的速度跑一段,但各人的速度不一定相同。两个队第一棒的队员同时同地开跑。那么,全程中最多可能发生( )次超越。(段的分界处的超越不计在内)
A.6 B.10 C.12 D.16
18.若十位数是39的整数倍,这样的十位数有( )个。
A.1 B.2 C.3 D.6
19.有6 个箱子,编号分别为1,2,3,…,6,各配一把钥匙,6把钥匙各不相同,每个箱子装入一把钥匙并锁好。先撬开1、2 号箱子,取出钥匙去开别的箱子,如果最终能把箱子都打开,则称为一种“好”的放钥匙的方法。“好”的放钥匙方法的总数是( )。
A.120 B.240 C.432 D.252
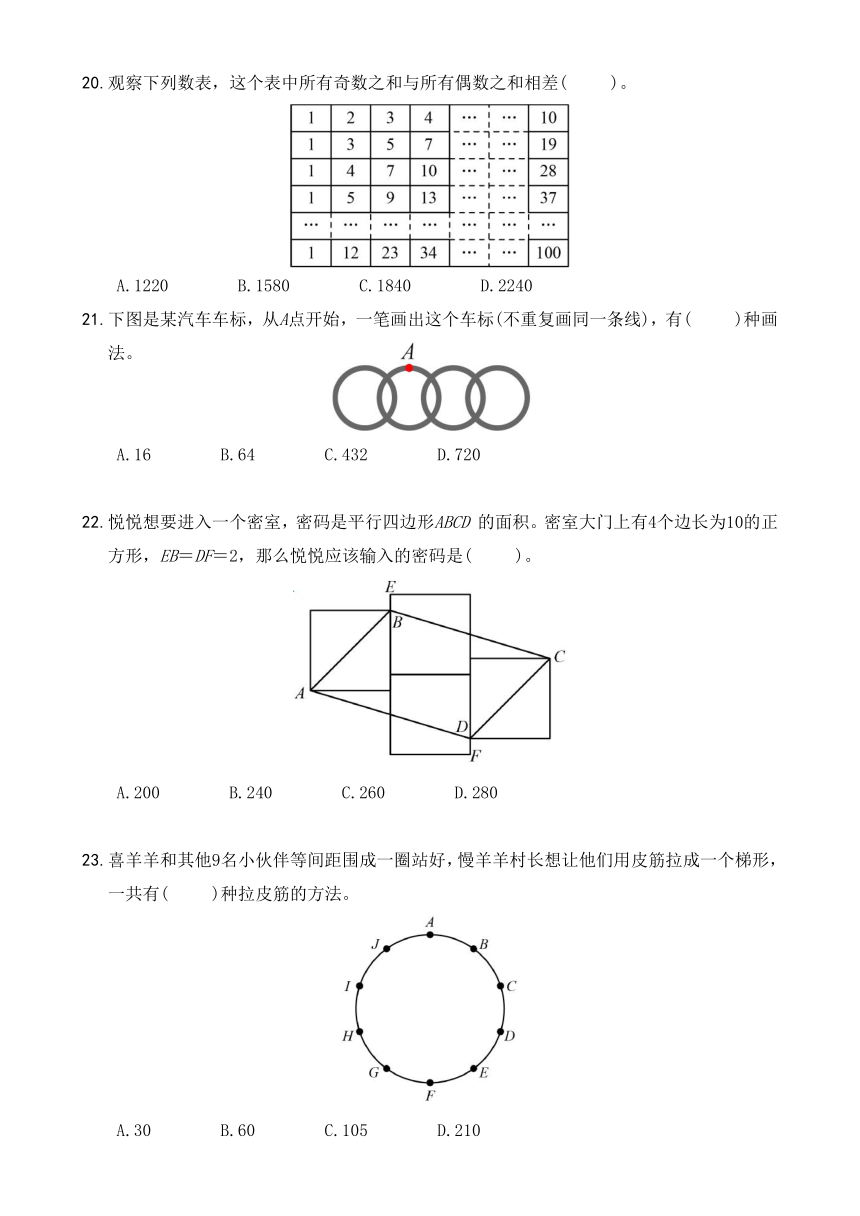
20.观察下列数表,这个表中所有奇数之和与所有偶数之和相差( )。
A.1220 B.1580 C.1840 D.2240
21.下图是某汽车车标,从A点开始,一笔画出这个车标(不重复画同一条线),有( )种画法。
A.16 B.64 C.432 D.720
22.悦悦想要进入一个密室,密码是平行四边形ABCD 的面积。密室大门上有4个边长为10的正方形,EB=DF=2,那么悦悦应该输入的密码是( )。
A.200 B.240 C.260 D.280
23.喜羊羊和其他9名小伙伴等间距围成一圈站好,慢羊羊村长想让他们用皮筋拉成一个梯形,一共有( )种拉皮筋的方法。
A.30 B.60 C.105 D.210
24.如图所示,将两个正四面体P-ABC 与Q-ABC 的一个面对接,组合成一个六面体。现用3种不同颜色对这个六面体的表面涂色,要求每个面只涂一种颜色,相邻的面均不同色,则不同的染色方案有( )种。
A.12 B.18 C.24 D.36
25.公路上,从前往后依次有一辆油罐车、一辆投石车和一辆救援车在向前行驶。油罐车边行驶边漏油,其他车辆如果接触到漏出的油,速度就会变成原来的一半。而救援车如果追上投石车,就会立刻被投石车发射出去,在空中向前瞬间移动出(时间忽略不计)投石车与救援车1秒所能前进的路程之和,并在落地后恢复到自己被发射前的速度。已知刚开始的时候,油罐车与投石车之间的距离是500米,投石车与救援车之间的距离是4000米,救援车的速度是投石车的3倍。如果救援车将被投石车扔出去时,二者距离油罐车刚好200米,而救援车落地瞬间刚好追上油罐车,那么油罐车的行驶速度是( )米/秒。
A.25 B.47.5 C.70 D.97.5
四年级奥数培优测试卷答案
1. 计算:1 2+3 4+ 98+99=( A )。
A.50 B.49 C.48 D.45
2.计算:2024÷(20+24)-2025÷(20+25)=( A )。
A.1 B.2 C.3 D.4
3.1949年,我国一年全国用电总量仅43亿千瓦时,人口总量约5.42亿人。而75年后的今天,我国全年用电总量达到了92241亿千瓦时,人口总量约14.1亿人,发电量增长超2000倍。在今天,我国每人每天平均用电量大约是75年前每人约( B )天的用电量。
A. 640 B. 800 C. 1200 D. 1800
4.计算 =( B )。
A. 1234567891011121314151617181716151413121110987654321
B. 12345679012345678987654320987654321
C. 123456789012345678987654320987654321
D. 123456790123456789876543210987654321
5.小可午饭时选择了一份可自行搭配的套餐,其中主菜有6种,可任选其中一种;配菜有4种,可任选其中一种;甜品有2种,可任选其中一种也可不选。小可的午饭共有( A )种搭配方案。
A. 72 B.60 C. 48 D. 36
6.下图是A,B,C,D 四个货场之间的道路示意图,□中的数是各货场储存的货物重量(单位:吨),道路上标注的数表示两货场之间的距离(单位:千米)。现在要把全部的货物集中到其中的一个货场中,如果每吨货物运输1千米需要付5元运输费,那么总运输费最少是( C )元。
A.3264 B.4464 C.16320 D.22320
7.阿呆和阿瓜各有一些藏书,如果阿瓜送给阿呆20本书,那么阿呆的藏书数量就是阿瓜的7倍;如果阿呆送给阿瓜20本书,那么阿呆的藏书数量就是阿瓜的3倍。原来阿呆的藏书有( C )本。
A.220 B. 240 C. 260 D.280
8.定义:对于整数a,b,c,若ac=b,则a@b=c。如:2@2=1,2@4=2,3@81=4。
3@3+32@34+33@39+......+3100@310000=( C )。
A. 150 B.2024 C. 5050 D. 12500
9.如图,在乘法竖式的每个空格中填入一个数字,使其成立,那么所得的乘积是( D )。
A.4332 B. 4324 C.4336 D.4346
10.一列火车通过长320米的隧道用了45秒。当它通过长680米的大桥时,速度比通过隧道时增加了2倍,结果用了30秒。火车通过大桥的速度是( B )米/秒。
A.30 B. 24 C. 20 D.8
11.三个正方形和一个直角三角形按如下方式组成的图形被称作毕达哥拉斯树。已知AB=6,BC=10,CD=8。连接AC、BD 交于点O,则S△COD-S△AOB=( A )。
A. 14 B. 16 C. 18 D. 20
12.已知7个小鸟积木可以换1个兔子积木,7个兔子积木可以换1个狐狸积木,7个狐狸积木可以换1个老虎积木。假如你有870个小鸟积木,你将能兑换的积木全部兑换后,还剩( D )个小鸟积木。
A.3 B.0 C.5 D.2
13.黑白棋子共有66枚,棋子只能放在一个足够大的正方体的顶点或棱上,棋子不能重叠放置,要求8个顶点处各有一枚黑棋,任意两枚黑棋之间至少有两枚白棋,那么这个正方体上最多能放( B )枚黑棋。
A.11 B.19 C.20 D.34
14.近些年电竞比赛中有一个非常流行的赛制叫瑞士轮,它指的是随机公平地编排第一轮比赛(一般由抽签决定),接着开始比赛。当某一轮比赛结束后,可以得到所有比赛选手的总积分(常见表达为胜场数—负场数,例如某个队伍2胜1负可以表示为2—1)。根据这个总积分的高低,把比赛选手由高到低排序(总积分相同则并列随机排序),接着是第1名对第2名,第3名对第4名,…,任何两队不重复对抗(若有两队之前比赛过,则微调排序使他们的对手都是之前没有比赛过的),如此循环,直到所有轮次结束。现在有16个队伍参加比赛,资格赛阶段采用单场定胜负的瑞士轮赛制,规定先达到3 胜场晋级,先达到3 负场淘汰,那么资格赛阶段共( D )场比赛。
A.36 B.32 C.20 D.33
15.唐僧师徒四人来到一片桃园摘桃充饥,唐僧吃了2个桃子,猪八戒吃的桃子数量是沙和尚的5 倍,沙和尚吃的桃子数量是孙悟空的一半。这时突然遭遇妖怪,降妖除魔后,每人又吃了一些桃子补充体力,这次他们吃的都一样多。最终发现四人前前后后一共在桃园吃了42个桃子,其中孙悟空吃了( D )个桃子。
A.6 B.8 C.9 D.10
16.有一些数字饼干按照如下规律排列成一个多位数:199019911992…2025,贪吃虫吃掉其中的100 块饼干后(不能改变饼干的顺序),剩下的多位数最小,那么这个多位数的数字之和是( D )。
A.4 B.6 C.8 D.10
17.MathClub举办800米接力赛,有两个队参加比赛,每个队各有6人。各个队按照自己的打算将全程分成6段(每一段的长度不一定相等),每个队员以恒定的速度跑一段,但各人的速度不一定相同。两个队第一棒的队员同时同地开跑。那么,全程中最多可能发生( B )次超越。(段的分界处的超越不计在内)
A.6 B.10 C.12 D.16
18.若十位数是39的整数倍,这样的十位数有( B )个。
A.1 B.2 C.3 D.6
19.有6 个箱子,编号分别为1,2,3,…,6,各配一把钥匙,6把钥匙各不相同,每个箱子装入一把钥匙并锁好。先撬开1、2 号箱子,取出钥匙去开别的箱子,如果最终能把箱子都打开,则称为一种“好”的放钥匙的方法。“好”的放钥匙方法的总数是( B )。
A.120 B.240 C.432 D.252
20.观察下列数表,这个表中所有奇数之和与所有偶数之和相差( A )。
A.1220 B.1580 C.1840 D.2240
21.下图是某汽车车标,从A点开始,一笔画出这个车标(不重复画同一条线),有( C )种画法。
A.16 B.64 C.432 D.720
22.悦悦想要进入一个密室,密码是平行四边形ABCD 的面积。密室大门上有4个边长为10的正方形,EB=DF=2,那么悦悦应该输入的密码是( C )。
A.200 B.240 C.260 D.280
23.喜羊羊和其他9名小伙伴等间距围成一圈站好,慢羊羊村长想让他们用皮筋拉成一个梯形,一共有( B )种拉皮筋的方法。
A.30 B.60 C.105 D.210
24.如图所示,将两个正四面体P-ABC 与Q-ABC 的一个面对接,组合成一个六面体。现用3种不同颜色对这个六面体的表面涂色,要求每个面只涂一种颜色,相邻的面均不同色,则不同的染色方案有( A )种。
A.12 B.18 C.24 D.36
25.公路上,从前往后依次有一辆油罐车、一辆投石车和一辆救援车在向前行驶。油罐车边行驶边漏油,其他车辆如果接触到漏出的油,速度就会变成原来的一半。而救援车如果追上投石车,就会立刻被投石车发射出去,在空中向前瞬间移动出(时间忽略不计)投石车与救援车1秒所能前进的路程之和,并在落地后恢复到自己被发射前的速度。已知刚开始的时候,油罐车与投石车之间的距离是500米,投石车与救援车之间的距离是4000米,救援车的速度是投石车的3倍。如果救援车将被投石车扔出去时,二者距离油罐车刚好200米,而救援车落地瞬间刚好追上油罐车,那么油罐车的行驶速度是( B )米/秒。
A.25 B.47.5 C.70 D.97.5
1. 计算:1 2+3 4+ 98+99=( )。
A.50 B.49 C.48 D.45
2.计算:2024÷(20+24)-2025÷(20+25)=( )。
A.1 B.2 C.3 D.4
3.1949年,我国一年全国用电总量仅43亿千瓦时,人口总量约5.42亿人。而75年后的今天,我国全年用电总量达到了92241亿千瓦时,人口总量约14.1亿人,发电量增长超2000倍。在今天,我国每人每天平均用电量大约是75年前每人约( )天的用电量。
A. 640 B. 800 C. 1200 D. 1800
4.计算 =( )。
A. 1234567891011121314151617181716151413121110987654321
B. 12345679012345678987654320987654321
C. 123456789012345678987654320987654321
D. 123456790123456789876543210987654321
5.小可午饭时选择了一份可自行搭配的套餐,其中主菜有6种,可任选其中一种;配菜有4种,可任选其中一种;甜品有2种,可任选其中一种也可不选。小可的午饭共有( )种搭配方案。
A. 72 B.60 C. 48 D. 36
6.下图是A,B,C,D 四个货场之间的道路示意图,□中的数是各货场储存的货物重量(单位:吨),道路上标注的数表示两货场之间的距离(单位:千米)。现在要把全部的货物集中到其中的一个货场中,如果每吨货物运输1千米需要付5元运输费,那么总运输费最少是( )元。
A.3264 B.4464 C.16320 D.22320
7.阿呆和阿瓜各有一些藏书,如果阿瓜送给阿呆20本书,那么阿呆的藏书数量就是阿瓜的7倍;如果阿呆送给阿瓜20本书,那么阿呆的藏书数量就是阿瓜的3倍。原来阿呆的藏书有( )本。
A.220 B. 240 C. 260 D.280
8.定义:对于整数a,b,c,若ac=b,则a@b=c。如:2@2=1,2@4=2,3@81=4。
3@3+32@34+33@39+......+3100@310000=( )。
A. 150 B.2024 C. 5050 D. 12500
9.如图,在乘法竖式的每个空格中填入一个数字,使其成立,那么所得的乘积是( )。
A.4332 B. 4324 C.4336 D.4346
10.一列火车通过长320米的隧道用了45秒。当它通过长680米的大桥时,速度比通过隧道时增加了2倍,结果用了30秒。火车通过大桥的速度是( )米/秒。
A.30 B. 24 C. 20 D.8
11.三个正方形和一个直角三角形按如下方式组成的图形被称作毕达哥拉斯树.已知AB=6,BC=10,CD=8。连接AC、BD 交于点O,则S△COD-S△AOB=( )。
A. 14 B. 16 C. 18 D. 20
12.已知7个小鸟积木可以换1个兔子积木,7个兔子积木可以换1个狐狸积木,7个狐狸积木可以换1个老虎积木。假如你有870个小鸟积木,你将能兑换的积木全部兑换后,还剩( )个小鸟积木。
A.3 B.0 C.5 D.2
13.黑白棋子共有66枚,棋子只能放在一个足够大的正方体的顶点或棱上,棋子不能重叠放置,要求8个顶点处各有一枚黑棋,任意两枚黑棋之间至少有两枚白棋,那么这个正方体上最多能放( )枚黑棋。
A.11 B.19 C.20 D.34
14.近些年电竞比赛中有一个非常流行的赛制叫瑞士轮,它指的是随机公平地编排第一轮比赛(一般由抽签决定),接着开始比赛。当某一轮比赛结束后,可以得到所有比赛选手的总积分(常见表达为胜场数—负场数,例如某个队伍2胜1负可以表示为2—1)。根据这个总积分的高低,把比赛选手由高到低排序(总积分相同则并列随机排序),接着是第1名对第2名,第3名对第4名,…,任何两队不重复对抗(若有两队之前比赛过,则微调排序使他们的对手都是之前没有比赛过的),如此循环,直到所有轮次结束。现在有16个队伍参加比赛,资格赛阶段采用单场定胜负的瑞士轮赛制,规定先达到3 胜场晋级,先达到3 负场淘汰,那么资格赛阶段共( )场比赛。
A.36 B.32 C.20 D.33
15.唐僧师徒四人来到一片桃园摘桃充饥,唐僧吃了2个桃子,猪八戒吃的桃子数量是沙和尚的5 倍,沙和尚吃的桃子数量是孙悟空的一半。这时突然遭遇妖怪,降妖除魔后,每人又吃了一些桃子补充体力,这次他们吃的都一样多。最终发现四人前前后后一共在桃园吃了42个桃子,其中孙悟空吃了( )个桃子。
A.6 B.8 C.9 D.10
16.有一些数字饼干按照如下规律排列成一个多位数:199019911992…2025,贪吃虫吃掉其中的100 块饼干后(不能改变饼干的顺序),剩下的多位数最小,那么这个多位数的数字之和是( )。
A.4 B.6 C.8 D.10
17.MathClub举办800米接力赛,有两个队参加比赛,每个队各有6人。各个队按照自己的打算将全程分成6段(每一段的长度不一定相等),每个队员以恒定的速度跑一段,但各人的速度不一定相同。两个队第一棒的队员同时同地开跑。那么,全程中最多可能发生( )次超越。(段的分界处的超越不计在内)
A.6 B.10 C.12 D.16
18.若十位数是39的整数倍,这样的十位数有( )个。
A.1 B.2 C.3 D.6
19.有6 个箱子,编号分别为1,2,3,…,6,各配一把钥匙,6把钥匙各不相同,每个箱子装入一把钥匙并锁好。先撬开1、2 号箱子,取出钥匙去开别的箱子,如果最终能把箱子都打开,则称为一种“好”的放钥匙的方法。“好”的放钥匙方法的总数是( )。
A.120 B.240 C.432 D.252
20.观察下列数表,这个表中所有奇数之和与所有偶数之和相差( )。
A.1220 B.1580 C.1840 D.2240
21.下图是某汽车车标,从A点开始,一笔画出这个车标(不重复画同一条线),有( )种画法。
A.16 B.64 C.432 D.720
22.悦悦想要进入一个密室,密码是平行四边形ABCD 的面积。密室大门上有4个边长为10的正方形,EB=DF=2,那么悦悦应该输入的密码是( )。
A.200 B.240 C.260 D.280
23.喜羊羊和其他9名小伙伴等间距围成一圈站好,慢羊羊村长想让他们用皮筋拉成一个梯形,一共有( )种拉皮筋的方法。
A.30 B.60 C.105 D.210
24.如图所示,将两个正四面体P-ABC 与Q-ABC 的一个面对接,组合成一个六面体。现用3种不同颜色对这个六面体的表面涂色,要求每个面只涂一种颜色,相邻的面均不同色,则不同的染色方案有( )种。
A.12 B.18 C.24 D.36
25.公路上,从前往后依次有一辆油罐车、一辆投石车和一辆救援车在向前行驶。油罐车边行驶边漏油,其他车辆如果接触到漏出的油,速度就会变成原来的一半。而救援车如果追上投石车,就会立刻被投石车发射出去,在空中向前瞬间移动出(时间忽略不计)投石车与救援车1秒所能前进的路程之和,并在落地后恢复到自己被发射前的速度。已知刚开始的时候,油罐车与投石车之间的距离是500米,投石车与救援车之间的距离是4000米,救援车的速度是投石车的3倍。如果救援车将被投石车扔出去时,二者距离油罐车刚好200米,而救援车落地瞬间刚好追上油罐车,那么油罐车的行驶速度是( )米/秒。
A.25 B.47.5 C.70 D.97.5
四年级奥数培优测试卷答案
1. 计算:1 2+3 4+ 98+99=( A )。
A.50 B.49 C.48 D.45
2.计算:2024÷(20+24)-2025÷(20+25)=( A )。
A.1 B.2 C.3 D.4
3.1949年,我国一年全国用电总量仅43亿千瓦时,人口总量约5.42亿人。而75年后的今天,我国全年用电总量达到了92241亿千瓦时,人口总量约14.1亿人,发电量增长超2000倍。在今天,我国每人每天平均用电量大约是75年前每人约( B )天的用电量。
A. 640 B. 800 C. 1200 D. 1800
4.计算 =( B )。
A. 1234567891011121314151617181716151413121110987654321
B. 12345679012345678987654320987654321
C. 123456789012345678987654320987654321
D. 123456790123456789876543210987654321
5.小可午饭时选择了一份可自行搭配的套餐,其中主菜有6种,可任选其中一种;配菜有4种,可任选其中一种;甜品有2种,可任选其中一种也可不选。小可的午饭共有( A )种搭配方案。
A. 72 B.60 C. 48 D. 36
6.下图是A,B,C,D 四个货场之间的道路示意图,□中的数是各货场储存的货物重量(单位:吨),道路上标注的数表示两货场之间的距离(单位:千米)。现在要把全部的货物集中到其中的一个货场中,如果每吨货物运输1千米需要付5元运输费,那么总运输费最少是( C )元。
A.3264 B.4464 C.16320 D.22320
7.阿呆和阿瓜各有一些藏书,如果阿瓜送给阿呆20本书,那么阿呆的藏书数量就是阿瓜的7倍;如果阿呆送给阿瓜20本书,那么阿呆的藏书数量就是阿瓜的3倍。原来阿呆的藏书有( C )本。
A.220 B. 240 C. 260 D.280
8.定义:对于整数a,b,c,若ac=b,则a@b=c。如:2@2=1,2@4=2,3@81=4。
3@3+32@34+33@39+......+3100@310000=( C )。
A. 150 B.2024 C. 5050 D. 12500
9.如图,在乘法竖式的每个空格中填入一个数字,使其成立,那么所得的乘积是( D )。
A.4332 B. 4324 C.4336 D.4346
10.一列火车通过长320米的隧道用了45秒。当它通过长680米的大桥时,速度比通过隧道时增加了2倍,结果用了30秒。火车通过大桥的速度是( B )米/秒。
A.30 B. 24 C. 20 D.8
11.三个正方形和一个直角三角形按如下方式组成的图形被称作毕达哥拉斯树。已知AB=6,BC=10,CD=8。连接AC、BD 交于点O,则S△COD-S△AOB=( A )。
A. 14 B. 16 C. 18 D. 20
12.已知7个小鸟积木可以换1个兔子积木,7个兔子积木可以换1个狐狸积木,7个狐狸积木可以换1个老虎积木。假如你有870个小鸟积木,你将能兑换的积木全部兑换后,还剩( D )个小鸟积木。
A.3 B.0 C.5 D.2
13.黑白棋子共有66枚,棋子只能放在一个足够大的正方体的顶点或棱上,棋子不能重叠放置,要求8个顶点处各有一枚黑棋,任意两枚黑棋之间至少有两枚白棋,那么这个正方体上最多能放( B )枚黑棋。
A.11 B.19 C.20 D.34
14.近些年电竞比赛中有一个非常流行的赛制叫瑞士轮,它指的是随机公平地编排第一轮比赛(一般由抽签决定),接着开始比赛。当某一轮比赛结束后,可以得到所有比赛选手的总积分(常见表达为胜场数—负场数,例如某个队伍2胜1负可以表示为2—1)。根据这个总积分的高低,把比赛选手由高到低排序(总积分相同则并列随机排序),接着是第1名对第2名,第3名对第4名,…,任何两队不重复对抗(若有两队之前比赛过,则微调排序使他们的对手都是之前没有比赛过的),如此循环,直到所有轮次结束。现在有16个队伍参加比赛,资格赛阶段采用单场定胜负的瑞士轮赛制,规定先达到3 胜场晋级,先达到3 负场淘汰,那么资格赛阶段共( D )场比赛。
A.36 B.32 C.20 D.33
15.唐僧师徒四人来到一片桃园摘桃充饥,唐僧吃了2个桃子,猪八戒吃的桃子数量是沙和尚的5 倍,沙和尚吃的桃子数量是孙悟空的一半。这时突然遭遇妖怪,降妖除魔后,每人又吃了一些桃子补充体力,这次他们吃的都一样多。最终发现四人前前后后一共在桃园吃了42个桃子,其中孙悟空吃了( D )个桃子。
A.6 B.8 C.9 D.10
16.有一些数字饼干按照如下规律排列成一个多位数:199019911992…2025,贪吃虫吃掉其中的100 块饼干后(不能改变饼干的顺序),剩下的多位数最小,那么这个多位数的数字之和是( D )。
A.4 B.6 C.8 D.10
17.MathClub举办800米接力赛,有两个队参加比赛,每个队各有6人。各个队按照自己的打算将全程分成6段(每一段的长度不一定相等),每个队员以恒定的速度跑一段,但各人的速度不一定相同。两个队第一棒的队员同时同地开跑。那么,全程中最多可能发生( B )次超越。(段的分界处的超越不计在内)
A.6 B.10 C.12 D.16
18.若十位数是39的整数倍,这样的十位数有( B )个。
A.1 B.2 C.3 D.6
19.有6 个箱子,编号分别为1,2,3,…,6,各配一把钥匙,6把钥匙各不相同,每个箱子装入一把钥匙并锁好。先撬开1、2 号箱子,取出钥匙去开别的箱子,如果最终能把箱子都打开,则称为一种“好”的放钥匙的方法。“好”的放钥匙方法的总数是( B )。
A.120 B.240 C.432 D.252
20.观察下列数表,这个表中所有奇数之和与所有偶数之和相差( A )。
A.1220 B.1580 C.1840 D.2240
21.下图是某汽车车标,从A点开始,一笔画出这个车标(不重复画同一条线),有( C )种画法。
A.16 B.64 C.432 D.720
22.悦悦想要进入一个密室,密码是平行四边形ABCD 的面积。密室大门上有4个边长为10的正方形,EB=DF=2,那么悦悦应该输入的密码是( C )。
A.200 B.240 C.260 D.280
23.喜羊羊和其他9名小伙伴等间距围成一圈站好,慢羊羊村长想让他们用皮筋拉成一个梯形,一共有( B )种拉皮筋的方法。
A.30 B.60 C.105 D.210
24.如图所示,将两个正四面体P-ABC 与Q-ABC 的一个面对接,组合成一个六面体。现用3种不同颜色对这个六面体的表面涂色,要求每个面只涂一种颜色,相邻的面均不同色,则不同的染色方案有( A )种。
A.12 B.18 C.24 D.36
25.公路上,从前往后依次有一辆油罐车、一辆投石车和一辆救援车在向前行驶。油罐车边行驶边漏油,其他车辆如果接触到漏出的油,速度就会变成原来的一半。而救援车如果追上投石车,就会立刻被投石车发射出去,在空中向前瞬间移动出(时间忽略不计)投石车与救援车1秒所能前进的路程之和,并在落地后恢复到自己被发射前的速度。已知刚开始的时候,油罐车与投石车之间的距离是500米,投石车与救援车之间的距离是4000米,救援车的速度是投石车的3倍。如果救援车将被投石车扔出去时,二者距离油罐车刚好200米,而救援车落地瞬间刚好追上油罐车,那么油罐车的行驶速度是( B )米/秒。
A.25 B.47.5 C.70 D.97.5
同课章节目录
