第一单元 第04课时 立体图形的展开和折叠(教学课件)(共33张PPT) 人教版 三年级上册数学
文档属性
| 名称 | 第一单元 第04课时 立体图形的展开和折叠(教学课件)(共33张PPT) 人教版 三年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 13:22:39 | ||
图片预览







文档简介
(共33张PPT)
第一单元 观察物体
第4课时 立体图形的展开和折叠
小学数学·三年级(上)·RJ
通过剪、折操作,建立立体图形与平面展开图的转化能力。
经历长方体展开图的形成过程,能正确识别展开图中的6个面及其相对关系。
掌握“相对的面形状相同且不相邻”的规律,判断简单展开图能否折成长方体。
理解长方体展开图中面的对应关系(相对面位置规律)。
想象不同剪法得到的展开图形状,理解“剪开边数固定但图形可变”。
通过剪、折操作,建立立体图形与平面展开图的转化能力。学会用数学语言描述剪开策略和发现的特征。
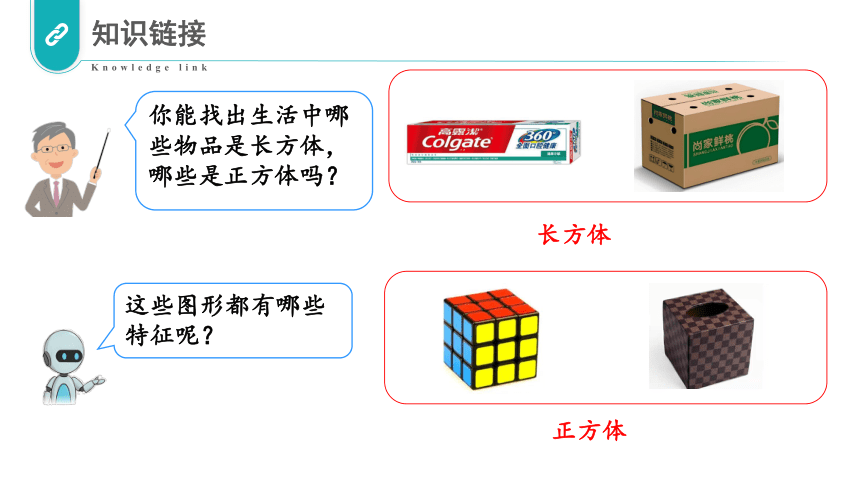
正方体
长方体
你能找出生活中哪些物品是长方体,哪些是正方体吗?
这些图形都有哪些特征呢?
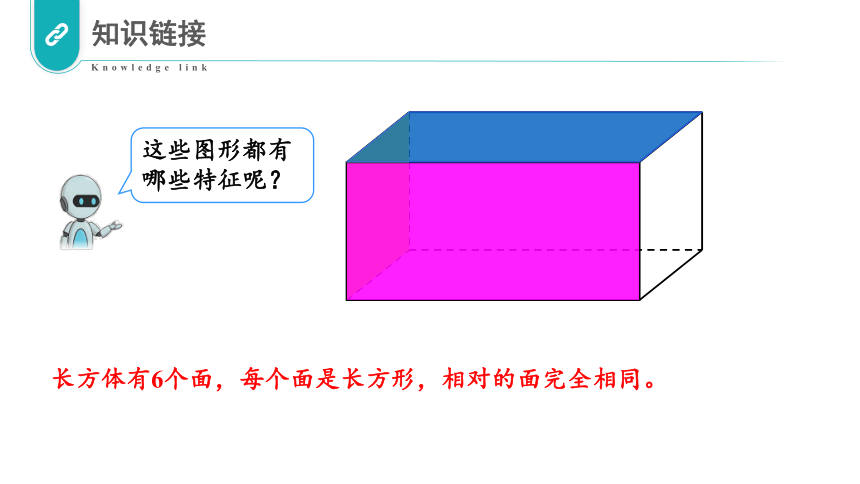
长方体有6个面,每个面是长方形,相对的面完全相同。
这些图形都有哪些特征呢?
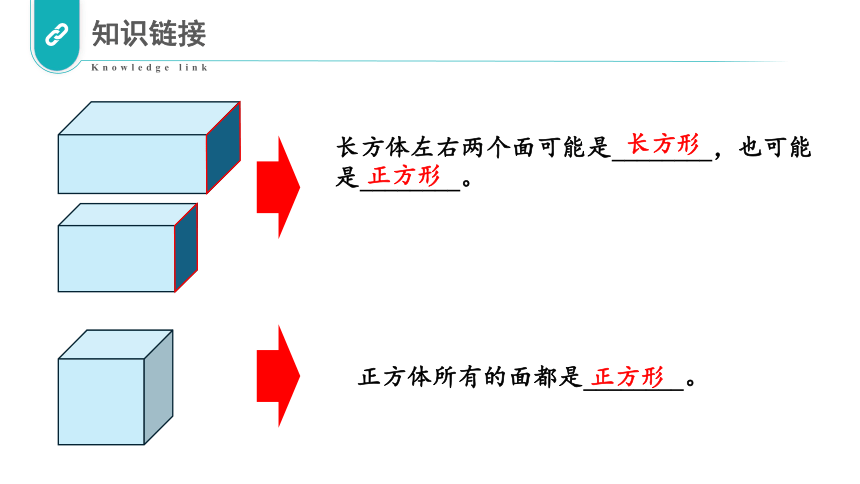
长方体左右两个面可能是________,也可能是________。
长方形
正方形
正方体所有的面都是________。
正方形
实物操作,要剪开几条边?
分析题意
把长方体纸盒剪开,平铺在桌面上。
注意:每个面都至少有一条边和其他的面相连。
(1)下面的几个纸盒都需要剪开几条边?想一想,描一描。
动手试一试!
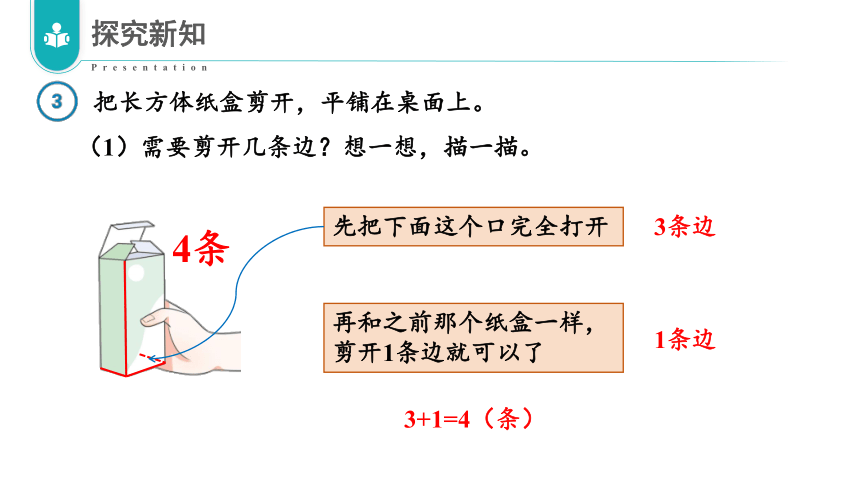
(1)需要剪开几条边?想一想,描一描。
1条
把长方体纸盒剪开,平铺在桌面上。
上下两个面开着,前、后、左、右4个面围在一起,剪开其中的1条边即可。
研究展开图时把这些接缝处多余的部分剪掉。
动手试一试!
(1)需要剪开几条边?想一想,描一描。
把长方体纸盒剪开,平铺在桌面上。
4条
先把下面这个口完全打开
再和之前那个纸盒一样,剪开1条边就可以了
3条边
1条边
3+1=4(条)
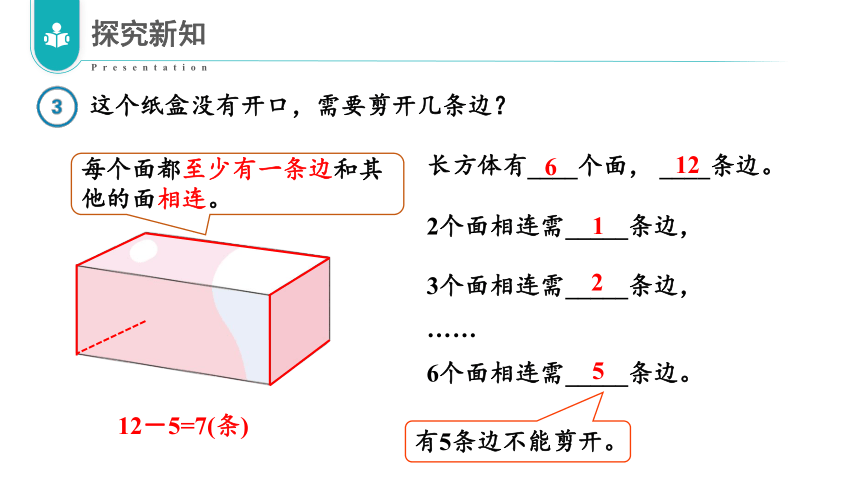
这个纸盒没有开口,需要剪开几条边?
每个面都至少有一条边和其他的面相连。
长方体有____个面, ____条边。
6
12
2个面相连需_____条边,
1
3个面相连需_____条边,
2
……
6个面相连需_____条边。
5
有5条边不能剪开。
12-5=7(条)
长方体的不同展开方式。
分析题意
(2)剪一剪,说一说。
要把接缝处多余的部分减掉哦!
观察剪开后的图形,说一说有什么特点?
(2)剪一剪,说一说。
这两个同样的纸盒,剪开的边不同,得到的展开图形也不同。
(2)剪一剪,说一说。
都有三组相同的面,每组中两个面都不相连。
(3)你能在剪开后的图形上找到原来纸盒上的6个面吗?想一想,说一说。
小组合作:
①看一看,折一折剪开后的长方体展开图。
②在展开图中标出上、下、前、后、左、右这6个面。
③小组选代表说一说你们是怎样找的。
方法一:折一折
前
前
我先确定从“前面”看到的那个面,再围起来看一看……
从而确定其他五个面
方法二:找对立面
前
前
后
后
上
下
左
右
与“前”形状相同的另一个长方形上
总结:“前”与“后”相对,,“上”和“下”相对,相对的面形状相同。
“后”与“前”相对,应该写在……
问题拓展:正方体可以怎样展开,你能想到多少种不同的展开方法?
“141”型:中间四个面,两边各一面。
“231”型:中间三个面,一、二隔河见。
“222”型:中间两个面,楼梯天天见。
“33”型:中间没有面,三、三连一线。
“Z”字头两端的两个面相对。
教材第4页“做一做”。
用附页1的图做一个长方体纸盒。先在图中标出从其他几个方向看到的面,再把它剪下来,围一围,看看标得对不对。
前
教材第5页“练习一第四题”
1.下面的图形能折成正方体吗?把附页2的图形剪下来折一折、试一试。
√
√
2.下面哪些图形沿虚线折叠后能围成一个正方体或长方体?能的在下面画“√”,不能的在下面画“×”。
√
×
√
×
√
√
3.将一个长方体形状的可动公仔盲盒沿着边拆开,图形如下,这个盲盒各个面相对的面是什么 填一填。
( )-( )
( )-( )
( )-( )
A
F
B
D
C
E
×
√
4.下面图形是沿着正方体纸盒的边剪开的吗 是的打“√”,不是的打“×”。
×
√
√
“田” 字型
围不成
5.用左边的铁皮能围成右边哪个立体图形?连一连。
上面是正方形
围不成
6.有一个正方体,六个面上分别写着数字1~6。从不同的角度观察,情况如下。那么数字1对面是数字( ),数字2对面是数字( ),数字3对面是数字( )。
5
4
6
1.对于开口不同的长方体纸盒,需要剪开的边的条数不同。
上下两端开口→剪1条边 只有一端开口→剪4条边 没有开口→剪7条边
2.长方体剪开后的图形中,相对的面完全相同且不相连。
上
下
前
后
左
右
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
第一单元 观察物体
第4课时 立体图形的展开和折叠
小学数学·三年级(上)·RJ
通过剪、折操作,建立立体图形与平面展开图的转化能力。
经历长方体展开图的形成过程,能正确识别展开图中的6个面及其相对关系。
掌握“相对的面形状相同且不相邻”的规律,判断简单展开图能否折成长方体。
理解长方体展开图中面的对应关系(相对面位置规律)。
想象不同剪法得到的展开图形状,理解“剪开边数固定但图形可变”。
通过剪、折操作,建立立体图形与平面展开图的转化能力。学会用数学语言描述剪开策略和发现的特征。
正方体
长方体
你能找出生活中哪些物品是长方体,哪些是正方体吗?
这些图形都有哪些特征呢?
长方体有6个面,每个面是长方形,相对的面完全相同。
这些图形都有哪些特征呢?
长方体左右两个面可能是________,也可能是________。
长方形
正方形
正方体所有的面都是________。
正方形
实物操作,要剪开几条边?
分析题意
把长方体纸盒剪开,平铺在桌面上。
注意:每个面都至少有一条边和其他的面相连。
(1)下面的几个纸盒都需要剪开几条边?想一想,描一描。
动手试一试!
(1)需要剪开几条边?想一想,描一描。
1条
把长方体纸盒剪开,平铺在桌面上。
上下两个面开着,前、后、左、右4个面围在一起,剪开其中的1条边即可。
研究展开图时把这些接缝处多余的部分剪掉。
动手试一试!
(1)需要剪开几条边?想一想,描一描。
把长方体纸盒剪开,平铺在桌面上。
4条
先把下面这个口完全打开
再和之前那个纸盒一样,剪开1条边就可以了
3条边
1条边
3+1=4(条)
这个纸盒没有开口,需要剪开几条边?
每个面都至少有一条边和其他的面相连。
长方体有____个面, ____条边。
6
12
2个面相连需_____条边,
1
3个面相连需_____条边,
2
……
6个面相连需_____条边。
5
有5条边不能剪开。
12-5=7(条)
长方体的不同展开方式。
分析题意
(2)剪一剪,说一说。
要把接缝处多余的部分减掉哦!
观察剪开后的图形,说一说有什么特点?
(2)剪一剪,说一说。
这两个同样的纸盒,剪开的边不同,得到的展开图形也不同。
(2)剪一剪,说一说。
都有三组相同的面,每组中两个面都不相连。
(3)你能在剪开后的图形上找到原来纸盒上的6个面吗?想一想,说一说。
小组合作:
①看一看,折一折剪开后的长方体展开图。
②在展开图中标出上、下、前、后、左、右这6个面。
③小组选代表说一说你们是怎样找的。
方法一:折一折
前
前
我先确定从“前面”看到的那个面,再围起来看一看……
从而确定其他五个面
方法二:找对立面
前
前
后
后
上
下
左
右
与“前”形状相同的另一个长方形上
总结:“前”与“后”相对,,“上”和“下”相对,相对的面形状相同。
“后”与“前”相对,应该写在……
问题拓展:正方体可以怎样展开,你能想到多少种不同的展开方法?
“141”型:中间四个面,两边各一面。
“231”型:中间三个面,一、二隔河见。
“222”型:中间两个面,楼梯天天见。
“33”型:中间没有面,三、三连一线。
“Z”字头两端的两个面相对。
教材第4页“做一做”。
用附页1的图做一个长方体纸盒。先在图中标出从其他几个方向看到的面,再把它剪下来,围一围,看看标得对不对。
前
教材第5页“练习一第四题”
1.下面的图形能折成正方体吗?把附页2的图形剪下来折一折、试一试。
√
√
2.下面哪些图形沿虚线折叠后能围成一个正方体或长方体?能的在下面画“√”,不能的在下面画“×”。
√
×
√
×
√
√
3.将一个长方体形状的可动公仔盲盒沿着边拆开,图形如下,这个盲盒各个面相对的面是什么 填一填。
( )-( )
( )-( )
( )-( )
A
F
B
D
C
E
×
√
4.下面图形是沿着正方体纸盒的边剪开的吗 是的打“√”,不是的打“×”。
×
√
√
“田” 字型
围不成
5.用左边的铁皮能围成右边哪个立体图形?连一连。
上面是正方形
围不成
6.有一个正方体,六个面上分别写着数字1~6。从不同的角度观察,情况如下。那么数字1对面是数字( ),数字2对面是数字( ),数字3对面是数字( )。
5
4
6
1.对于开口不同的长方体纸盒,需要剪开的边的条数不同。
上下两端开口→剪1条边 只有一端开口→剪4条边 没有开口→剪7条边
2.长方体剪开后的图形中,相对的面完全相同且不相连。
上
下
前
后
左
右
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
同课章节目录
