五年级奥数培优测试卷(含答案)
图片预览



文档简介
五年级奥数培优测试卷
1. 计算:2012+2012-2012×2012×2÷2012=( )。
A.0 B.1 C.2 D.2022
2.计算:×5÷2=( )。
A. B. C. D.
3.计算: 2026÷2024=( )。
4.计算:(1+)×(1+) ×(1+) ×……×(1+)=( )。
A. B. C. D.
5.如图,正六边形面积为18,那么阴影部分面积为( )。
A.9 B.8 C.7 D.6
6.甲、乙两个仓库各存粮若干,先将甲仓库中粮食的运到乙仓库,再将乙仓库此时粮食的运到甲仓库,这时甲仓库有粮食720吨,乙仓库有粮食600吨。那么原来甲仓库存粮( )吨,乙仓库存粮( )吨。
A.670;650 B.650;670 C.800;520 D.520;800
7.如图,把四边形ABCD各边都延长1倍,得到一个新四边形EFGH。如果四边形ABCD的面积是5平方厘米,则四边形EFGH的面积是( )平方厘米。
A.10 B.20 C.25 D.30
8.甲、乙、丙、丁、戊、己6人排成一排照相,若甲、乙两人不能相邻,丙、丁两人也不能相邻,那么一共有( )种不同的排法。
A.224 B.316 C.328 D.336
9.黑板上写着1~2024共2024个自然数,汤姆每次擦去两个奇偶性相同的数,再写上它们的平均数,直到黑板上只剩下一个自然数为止。最后剩下的这个自然数最大可能是( )。
A. 2024 B. 2023 C. 2022 D. 2021
10.有一类有趣的数,它的因数个数也是自身的一个因数。例如9有3个因数,而3恰好也是9的因数,那么9就属于这一类有趣的数。1000以内共有( )个奇数是有趣的数。
A.101 B. 53 C.25 D.5
11.用8个1×2的小长方形去覆盖2×8的方格网,一共有( )种不同的覆盖方法。
A.21 B.19 C.55 D. 34
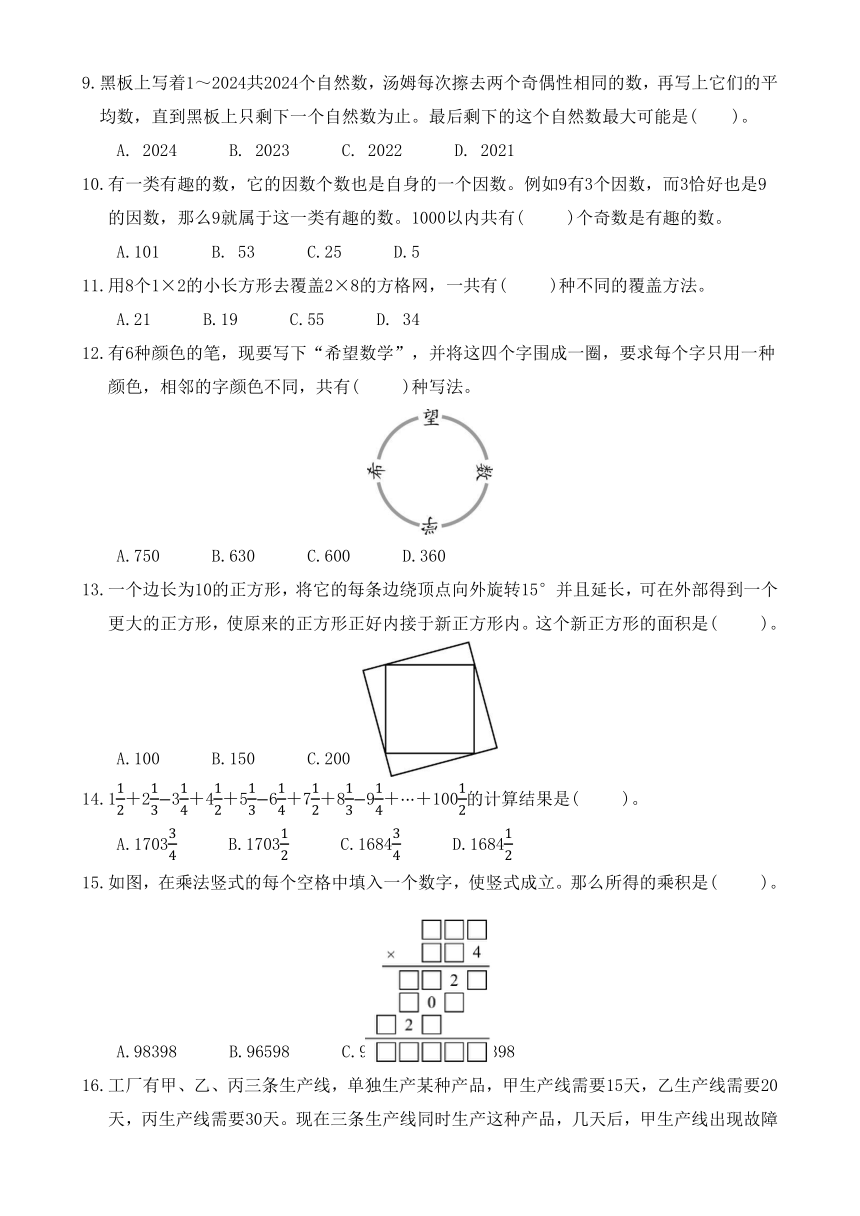
12.有6种颜色的笔,现要写下“希望数学”,并将这四个字围成一圈,要求每个字只用一种颜色,相邻的字颜色不同,共有( )种写法。
A.750 B.630 C.600 D.360
13.一个边长为10的正方形,将它的每条边绕顶点向外旋转15°并且延长,可在外部得到一个更大的正方形,使原来的正方形正好内接于新正方形内。这个新正方形的面积是( )。
A.100 B.150 C.200 D.250
14.1+2 3+4+5 6+7+8 9+ +100的计算结果是( )。
A.1703 B.1703 C.1684 D.1684
15.如图,在乘法竖式的每个空格中填入一个数字,使竖式成立。那么所得的乘积是( )。
A.98398 B.96598 C.97698 D.96398
16.工厂有甲、乙、丙三条生产线,单独生产某种产品,甲生产线需要15天,乙生产线需要20天,丙生产线需要30天。现在三条生产线同时生产这种产品,几天后,甲生产线出现故障停产,乙、丙两条生产线继续生产,又过了3天完成任务。那么甲生产线生产了( )天。
A.3 B.4 C.5 D.6
17.我们把恰好含有两个0的自然数称为“希望数”,例如100,2008,2020,...等。那么共有( )个四位“希望数”。
A.243 B.270 C.216 D.486
18.有红、黄、蓝、绿四种颜色的球各若干个,放在一个袋子里。每次从袋子里取出两个球,记录下它们的颜色组合后放回袋子里。经过多次取球后,发现取出的颜色组合有红和黄、红和蓝、红和绿、黄和蓝、黄和绿、蓝和绿这六种情况,且每种情况出现的次数分别为10次、12次、8次、9次、11次、7次。那么,在以上取球过程中,哪种颜色的球被取出的次数最少?( )
A.红色 B.黄色 C.蓝色 D.绿色
19.已知多位数 能同时被7和13整除,则方框内的数字分别是( )。
A.0;9 B.6;9 C.7;4 D.7;3
20.甲、乙、丙三人同时从A地出发前往B地,甲骑自行车,速度是每小时15千米;乙步行,速度是每小时5千米;丙开汽车,速度是每小时45千米。丙先带甲行驶一段路程后,再让甲自己骑车前往B地,然后返回接乙前往B地,最后三人同时到达B地。已知A、B两地的距离是90千米,则丙从出发到B地一共用了( )小时。
A. B. C. D.
21.一个圆上有9个不同的点,以它们为顶点连接3个三角形,这3个三角形的边在圆内都不相交,共有( )种不同的连法。
A.8 B.6 C.12 D.3
22.如图,在平行四边形ABCD中,E和H是AD和BC的中点,F和G是AB的三等分点。已知平行四边形ABCD的面积是160,那么四边形FGKI的面积是( )。
A. 16 B. 18
C. 20 D. 22
23.从1~2001这2001个数中最多选出( )个数,保证取出的数中任何两个数的差既不等于2也不等于5。
A.855 B.856 C.857 D.858
24.一层楼有8个房间,标有1~8的序号,每个房间最多住1人,房间序号为质数的人总说假话,房间序号为合数的人总说真话,其余的人可能说真话也可能说假话。目前有6人入住这层楼,这6人的对话如下:
A:我住在2号房间。
B:我住在5号房间。
C:我住在8号房间。
D:我的房间序号是一个质数。
E:序号为偶数的房间已经住满了。
F:我的房间序号是六人里面最大的。
若无人入住的是p号房间和q号房间,那么p+q=( )。
A.8 B.9 C.10 D.11
25.已知p、q、r、s都是100以内互不相同的质数,且p+q2+r3+s4=1123,则p+q+r+s= ( )。
A.107 B.109 C.111 D.113
五年级奥数培优测试卷答案
1. 计算:2012+2012-2012×2012×2÷2012=( A )。
A.0 B.1 C.2 D.2022
2.计算:×5÷2=( A )。
A. B. C. D.
3.计算: 2026÷2024=( A )。
4.计算:(1+)×(1+) ×(1+) ×……×(1+)=( C )。
A. B. C. D.
5.如图,正六边形面积为18,那么阴影部分面积为( B )。
A.9 B.8 C.7 D.6
6.甲、乙两个仓库各存粮若干,先将甲仓库中粮食的运到乙仓库,再将乙仓库此时粮食的运到甲仓库,这时甲仓库有粮食720吨,乙仓库有粮食600吨。那么原来甲仓库存粮( B )吨,乙仓库存粮( )吨。
A.670;650 B.650;670 C.800;520 D.520;800
7.如图,把四边形ABCD各边都延长1倍,得到一个新四边形EFGH。如果四边形ABCD的面积是5平方厘米,则四边形EFGH的面积是( C )平方厘米。
A.10 B.20 C.25 D.30
8.甲、乙、丙、丁、戊、己6人排成一排照相,若甲、乙两人不能相邻,丙、丁两人也不能相邻,那么一共有( D )种不同的排法。
A.224 B.316 C.328 D.336
9.黑板上写着1~2024共2024个自然数,汤姆每次擦去两个奇偶性相同的数,再写上它们的平均数,直到黑板上只剩下一个自然数为止。最后剩下的这个自然数最大可能是( B )。
A. 2024 B. 2023 C. 2022 D. 2021
10.有一类有趣的数,它的因数个数也是自身的一个因数。例如9有3个因数,而3恰好也是9的因数,那么9就属于这一类有趣的数。1000以内共有( D )个奇数是有趣的数。
A.101 B. 53 C.25 D.5
11.用8个1×2的小长方形去覆盖2×8的方格网,一共有( D )种不同的覆盖方法。
A.21 B.19 C.55 D. 34
12.有6种颜色的笔,现要写下“希望数学”,并将这四个字围成一圈,要求每个字只用一种颜色,相邻的字颜色不同,共有( B )种写法。
A.750 B.630 C.600 D.360
13.一个边长为10的正方形,将它的每条边绕顶点向外旋转15°并且延长,可在外部得到一个更大的正方形,使原来的正方形正好内接于新正方形内。这个新正方形的面积是( B )。
A.100 B.150 C.200 D.250
14.1+2 3+4+5 6+7+8 9+ +100的计算结果是( A )。
A.1703 B.1703 C.1684 D.1684
15.如图,在乘法竖式的每个空格中填入一个数字,使竖式成立。那么所得的乘积是( D )。
A.98398 B.96598 C.97698 D.96398
16.工厂有甲、乙、丙三条生产线,单独生产某种产品,甲生产线需要15天,乙生产线需要20天,丙生产线需要30天。现在三条生产线同时生产这种产品,几天后,甲生产线出现故障停产,乙、丙两条生产线继续生产,又过了3天完成任务。那么甲生产线生产了( C )天。
A.3 B.4 C.5 D.6
17.我们把恰好含有两个0的自然数称为“希望数”,例如100,2008,2020,...等。那么共有( A )个四位“希望数”。
A.243 B.270 C.216 D.486
18.有红、黄、蓝、绿四种颜色的球各若干个,放在一个袋子里。每次从袋子里取出两个球,记录下它们的颜色组合后放回袋子里。经过多次取球后,发现取出的颜色组合有红和黄、红和蓝、红和绿、黄和蓝、黄和绿、蓝和绿这六种情况,且每种情况出现的次数分别为10次、12次、8次、9次、11次、7次。那么,在以上取球过程中,哪种颜色的球被取出的次数最少?( C )
A.红色 B.黄色 C.蓝色 D.绿色
19.已知多位数 能同时被7和13整除,则方框内的数字分别是( B )。
A.0;9 B.6;9 C.7;4 D.7;3
20.甲、乙、丙三人同时从A地出发前往B地,甲骑自行车,速度是每小时15千米;乙步行,速度是每小时5千米;丙开汽车,速度是每小时45千米。丙先带甲行驶一段路程后,再让甲自己骑车前往B地,然后返回接乙前往B地,最后三人同时到达B地。已知A、B两地的距离是90千米,则丙从出发到B地一共用了( C )小时。
A. B. C. D.
21.一个圆上有9个不同的点,以它们为顶点连接3个三角形,这3个三角形的边在圆内都不相交,共有( B )种不同的连法。
A.8 B.6 C.12 D.3
22.如图,在平行四边形ABCD中,E和H是AD和BC的中点,F和G是AB的三等分点。已知平行四边形ABCD的面积是160,那么四边形FGKI的面积是( D )。
A. 16 B. 18
C. 20 D. 22
23.从1~2001这2001个数中最多选出( D )个数,保证取出的数中任何两个数的差既不等于2也不等于5。
A.855 B.856 C.857 D.858
24.一层楼有8个房间,标有1~8的序号,每个房间最多住1人,房间序号为质数的人总说假话,房间序号为合数的人总说真话,其余的人可能说真话也可能说假话。目前有6人入住这层楼,这6人的对话如下:
A:我住在2号房间。
B:我住在5号房间。
C:我住在8号房间。
D:我的房间序号是一个质数。
E:序号为偶数的房间已经住满了。
F:我的房间序号是六人里面最大的。
若无人入住的是p号房间和q号房间,那么p+q=( C )。
A.8 B.9 C.10 D.11
25.已知p、q、r、s都是100以内互不相同的质数,且p+q2+r3+s4=1123,则p+q+r+s= ( B )。
A.107 B.109 C.111 D.113
1. 计算:2012+2012-2012×2012×2÷2012=( )。
A.0 B.1 C.2 D.2022
2.计算:×5÷2=( )。
A. B. C. D.
3.计算: 2026÷2024=( )。
4.计算:(1+)×(1+) ×(1+) ×……×(1+)=( )。
A. B. C. D.
5.如图,正六边形面积为18,那么阴影部分面积为( )。
A.9 B.8 C.7 D.6
6.甲、乙两个仓库各存粮若干,先将甲仓库中粮食的运到乙仓库,再将乙仓库此时粮食的运到甲仓库,这时甲仓库有粮食720吨,乙仓库有粮食600吨。那么原来甲仓库存粮( )吨,乙仓库存粮( )吨。
A.670;650 B.650;670 C.800;520 D.520;800
7.如图,把四边形ABCD各边都延长1倍,得到一个新四边形EFGH。如果四边形ABCD的面积是5平方厘米,则四边形EFGH的面积是( )平方厘米。
A.10 B.20 C.25 D.30
8.甲、乙、丙、丁、戊、己6人排成一排照相,若甲、乙两人不能相邻,丙、丁两人也不能相邻,那么一共有( )种不同的排法。
A.224 B.316 C.328 D.336
9.黑板上写着1~2024共2024个自然数,汤姆每次擦去两个奇偶性相同的数,再写上它们的平均数,直到黑板上只剩下一个自然数为止。最后剩下的这个自然数最大可能是( )。
A. 2024 B. 2023 C. 2022 D. 2021
10.有一类有趣的数,它的因数个数也是自身的一个因数。例如9有3个因数,而3恰好也是9的因数,那么9就属于这一类有趣的数。1000以内共有( )个奇数是有趣的数。
A.101 B. 53 C.25 D.5
11.用8个1×2的小长方形去覆盖2×8的方格网,一共有( )种不同的覆盖方法。
A.21 B.19 C.55 D. 34
12.有6种颜色的笔,现要写下“希望数学”,并将这四个字围成一圈,要求每个字只用一种颜色,相邻的字颜色不同,共有( )种写法。
A.750 B.630 C.600 D.360
13.一个边长为10的正方形,将它的每条边绕顶点向外旋转15°并且延长,可在外部得到一个更大的正方形,使原来的正方形正好内接于新正方形内。这个新正方形的面积是( )。
A.100 B.150 C.200 D.250
14.1+2 3+4+5 6+7+8 9+ +100的计算结果是( )。
A.1703 B.1703 C.1684 D.1684
15.如图,在乘法竖式的每个空格中填入一个数字,使竖式成立。那么所得的乘积是( )。
A.98398 B.96598 C.97698 D.96398
16.工厂有甲、乙、丙三条生产线,单独生产某种产品,甲生产线需要15天,乙生产线需要20天,丙生产线需要30天。现在三条生产线同时生产这种产品,几天后,甲生产线出现故障停产,乙、丙两条生产线继续生产,又过了3天完成任务。那么甲生产线生产了( )天。
A.3 B.4 C.5 D.6
17.我们把恰好含有两个0的自然数称为“希望数”,例如100,2008,2020,...等。那么共有( )个四位“希望数”。
A.243 B.270 C.216 D.486
18.有红、黄、蓝、绿四种颜色的球各若干个,放在一个袋子里。每次从袋子里取出两个球,记录下它们的颜色组合后放回袋子里。经过多次取球后,发现取出的颜色组合有红和黄、红和蓝、红和绿、黄和蓝、黄和绿、蓝和绿这六种情况,且每种情况出现的次数分别为10次、12次、8次、9次、11次、7次。那么,在以上取球过程中,哪种颜色的球被取出的次数最少?( )
A.红色 B.黄色 C.蓝色 D.绿色
19.已知多位数 能同时被7和13整除,则方框内的数字分别是( )。
A.0;9 B.6;9 C.7;4 D.7;3
20.甲、乙、丙三人同时从A地出发前往B地,甲骑自行车,速度是每小时15千米;乙步行,速度是每小时5千米;丙开汽车,速度是每小时45千米。丙先带甲行驶一段路程后,再让甲自己骑车前往B地,然后返回接乙前往B地,最后三人同时到达B地。已知A、B两地的距离是90千米,则丙从出发到B地一共用了( )小时。
A. B. C. D.
21.一个圆上有9个不同的点,以它们为顶点连接3个三角形,这3个三角形的边在圆内都不相交,共有( )种不同的连法。
A.8 B.6 C.12 D.3
22.如图,在平行四边形ABCD中,E和H是AD和BC的中点,F和G是AB的三等分点。已知平行四边形ABCD的面积是160,那么四边形FGKI的面积是( )。
A. 16 B. 18
C. 20 D. 22
23.从1~2001这2001个数中最多选出( )个数,保证取出的数中任何两个数的差既不等于2也不等于5。
A.855 B.856 C.857 D.858
24.一层楼有8个房间,标有1~8的序号,每个房间最多住1人,房间序号为质数的人总说假话,房间序号为合数的人总说真话,其余的人可能说真话也可能说假话。目前有6人入住这层楼,这6人的对话如下:
A:我住在2号房间。
B:我住在5号房间。
C:我住在8号房间。
D:我的房间序号是一个质数。
E:序号为偶数的房间已经住满了。
F:我的房间序号是六人里面最大的。
若无人入住的是p号房间和q号房间,那么p+q=( )。
A.8 B.9 C.10 D.11
25.已知p、q、r、s都是100以内互不相同的质数,且p+q2+r3+s4=1123,则p+q+r+s= ( )。
A.107 B.109 C.111 D.113
五年级奥数培优测试卷答案
1. 计算:2012+2012-2012×2012×2÷2012=( A )。
A.0 B.1 C.2 D.2022
2.计算:×5÷2=( A )。
A. B. C. D.
3.计算: 2026÷2024=( A )。
4.计算:(1+)×(1+) ×(1+) ×……×(1+)=( C )。
A. B. C. D.
5.如图,正六边形面积为18,那么阴影部分面积为( B )。
A.9 B.8 C.7 D.6
6.甲、乙两个仓库各存粮若干,先将甲仓库中粮食的运到乙仓库,再将乙仓库此时粮食的运到甲仓库,这时甲仓库有粮食720吨,乙仓库有粮食600吨。那么原来甲仓库存粮( B )吨,乙仓库存粮( )吨。
A.670;650 B.650;670 C.800;520 D.520;800
7.如图,把四边形ABCD各边都延长1倍,得到一个新四边形EFGH。如果四边形ABCD的面积是5平方厘米,则四边形EFGH的面积是( C )平方厘米。
A.10 B.20 C.25 D.30
8.甲、乙、丙、丁、戊、己6人排成一排照相,若甲、乙两人不能相邻,丙、丁两人也不能相邻,那么一共有( D )种不同的排法。
A.224 B.316 C.328 D.336
9.黑板上写着1~2024共2024个自然数,汤姆每次擦去两个奇偶性相同的数,再写上它们的平均数,直到黑板上只剩下一个自然数为止。最后剩下的这个自然数最大可能是( B )。
A. 2024 B. 2023 C. 2022 D. 2021
10.有一类有趣的数,它的因数个数也是自身的一个因数。例如9有3个因数,而3恰好也是9的因数,那么9就属于这一类有趣的数。1000以内共有( D )个奇数是有趣的数。
A.101 B. 53 C.25 D.5
11.用8个1×2的小长方形去覆盖2×8的方格网,一共有( D )种不同的覆盖方法。
A.21 B.19 C.55 D. 34
12.有6种颜色的笔,现要写下“希望数学”,并将这四个字围成一圈,要求每个字只用一种颜色,相邻的字颜色不同,共有( B )种写法。
A.750 B.630 C.600 D.360
13.一个边长为10的正方形,将它的每条边绕顶点向外旋转15°并且延长,可在外部得到一个更大的正方形,使原来的正方形正好内接于新正方形内。这个新正方形的面积是( B )。
A.100 B.150 C.200 D.250
14.1+2 3+4+5 6+7+8 9+ +100的计算结果是( A )。
A.1703 B.1703 C.1684 D.1684
15.如图,在乘法竖式的每个空格中填入一个数字,使竖式成立。那么所得的乘积是( D )。
A.98398 B.96598 C.97698 D.96398
16.工厂有甲、乙、丙三条生产线,单独生产某种产品,甲生产线需要15天,乙生产线需要20天,丙生产线需要30天。现在三条生产线同时生产这种产品,几天后,甲生产线出现故障停产,乙、丙两条生产线继续生产,又过了3天完成任务。那么甲生产线生产了( C )天。
A.3 B.4 C.5 D.6
17.我们把恰好含有两个0的自然数称为“希望数”,例如100,2008,2020,...等。那么共有( A )个四位“希望数”。
A.243 B.270 C.216 D.486
18.有红、黄、蓝、绿四种颜色的球各若干个,放在一个袋子里。每次从袋子里取出两个球,记录下它们的颜色组合后放回袋子里。经过多次取球后,发现取出的颜色组合有红和黄、红和蓝、红和绿、黄和蓝、黄和绿、蓝和绿这六种情况,且每种情况出现的次数分别为10次、12次、8次、9次、11次、7次。那么,在以上取球过程中,哪种颜色的球被取出的次数最少?( C )
A.红色 B.黄色 C.蓝色 D.绿色
19.已知多位数 能同时被7和13整除,则方框内的数字分别是( B )。
A.0;9 B.6;9 C.7;4 D.7;3
20.甲、乙、丙三人同时从A地出发前往B地,甲骑自行车,速度是每小时15千米;乙步行,速度是每小时5千米;丙开汽车,速度是每小时45千米。丙先带甲行驶一段路程后,再让甲自己骑车前往B地,然后返回接乙前往B地,最后三人同时到达B地。已知A、B两地的距离是90千米,则丙从出发到B地一共用了( C )小时。
A. B. C. D.
21.一个圆上有9个不同的点,以它们为顶点连接3个三角形,这3个三角形的边在圆内都不相交,共有( B )种不同的连法。
A.8 B.6 C.12 D.3
22.如图,在平行四边形ABCD中,E和H是AD和BC的中点,F和G是AB的三等分点。已知平行四边形ABCD的面积是160,那么四边形FGKI的面积是( D )。
A. 16 B. 18
C. 20 D. 22
23.从1~2001这2001个数中最多选出( D )个数,保证取出的数中任何两个数的差既不等于2也不等于5。
A.855 B.856 C.857 D.858
24.一层楼有8个房间,标有1~8的序号,每个房间最多住1人,房间序号为质数的人总说假话,房间序号为合数的人总说真话,其余的人可能说真话也可能说假话。目前有6人入住这层楼,这6人的对话如下:
A:我住在2号房间。
B:我住在5号房间。
C:我住在8号房间。
D:我的房间序号是一个质数。
E:序号为偶数的房间已经住满了。
F:我的房间序号是六人里面最大的。
若无人入住的是p号房间和q号房间,那么p+q=( C )。
A.8 B.9 C.10 D.11
25.已知p、q、r、s都是100以内互不相同的质数,且p+q2+r3+s4=1123,则p+q+r+s= ( B )。
A.107 B.109 C.111 D.113
同课章节目录
