24.1 圆的有关性质 提能集训(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 24.1 圆的有关性质 提能集训(含答案) 2025-2026学年数学人教版九年级上册 | 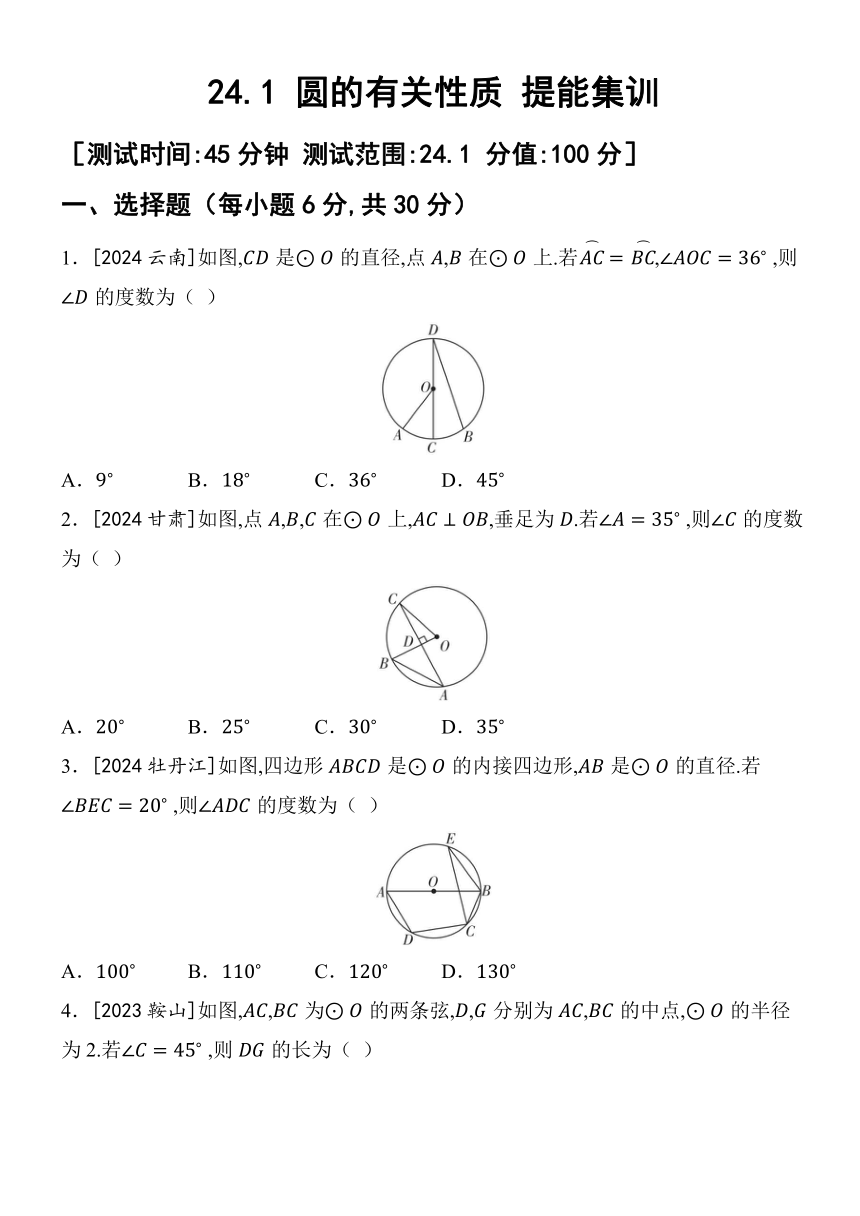 | |
| 格式 | docx | ||
| 文件大小 | 139.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 13:56:55 | ||
图片预览


文档简介
24.1 圆的有关性质 提能集训
[测试时间:45分钟 测试范围:24.1 分值:100分]
一、选择题(每小题6分,共30分)
1.[2024云南]如图,是的直径,点,在上.若, ,则的度数为( )
A. B. C. D.
2.[2024甘肃]如图,点,,在上,,垂足为.若 ,则的度数为( )
A. B. C. D.
3.[2024牡丹江]如图,四边形是的内接四边形,是的直径.若 ,则的度数为( )
A. B. C. D.
4.[2023鞍山]如图,,为的两条弦,,分别为,的中点,的半径为2.若 ,则的长为( )
A.2 B. C. D.
5.如图,,,是上的三点,且四边形是平行四边形,交于点,则的度数为( )
A. B. C. D.
二、填空题(每小题6分,共30分)
6.[2024枣庄]如图,是的内接三角形.若, ,则_ _ _ _ _ _ .
7.[2023南充]如图,是的直径,,分别是弦和的中点,若,,则的长是_ _ .
8.如图,,,,四点均在上, ,,则_ _ _ _ _ _ _ _ _ _ _ _ .
9.如图,经过五边形的四个顶点.若 , , ,则_ _ _ _ _ _ _ _ .
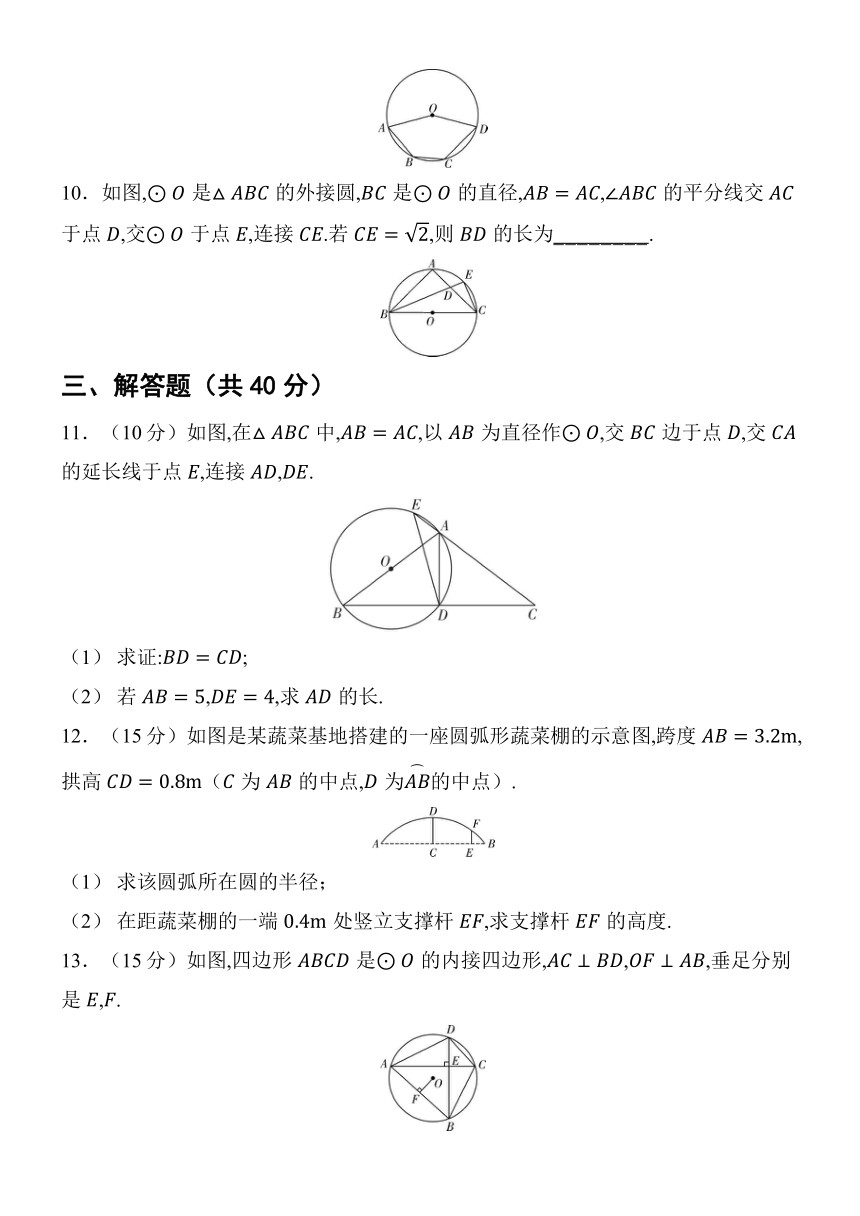
10.如图,是的外接圆,是的直径,,的平分线交于点,交于点,连接.若,则的长为_ _ _ _ _ _ _ _ .
三、解答题(共40分)
11.(10分)如图,在中,,以为直径作,交边于点,交的延长线于点,连接,.
(1) 求证:;
(2) 若,,求的长.
12.(15分)如图是某蔬菜基地搭建的一座圆弧形蔬菜棚的示意图,跨度,拱高(为的中点,为的中点).
(1) 求该圆弧所在圆的半径;
(2) 在距蔬菜棚的一端处竖立支撑杆,求支撑杆的高度.
13.(15分)如图,四边形是的内接四边形,,,垂足分别是,.
(1) 写出与的数量关系,并证明你的结论;
(2) 若,,求的半径.
一、选择题(每小题6分,共30分)
1.B 2.A 3.B 4.D 5.B
二、填空题(每小题6分,共30分)
6.
7.4
8.
9.
10.
三、解答题(共40分)
11.(1) 证明:是的直径,
,.
又,.
(2) 解:,,
,.
,,
.
是的直径, ,
,
.
12.(1) 解:为的中点,于点,
.
设所在的圆心为点,延长经过点,如答图.
第12题答图
设的半径为.
在中,,
,解得,
即该圆弧所在圆的半径为.
(2) 如答图,连接,过点作,交的延长线于点,
则.
在中,.
,
.
13.(1) 解:结论:.
证明:如答图,连接并延长交于点,连接.
,.
,
是的中位线,
.
是的直径, ,
.
, ,
.
,,
所对弧上的圆心角等于所对弧上的圆心角,
,.
第13题答图
(2) 由(1),得.
在中,,
,
的半径为.
[测试时间:45分钟 测试范围:24.1 分值:100分]
一、选择题(每小题6分,共30分)
1.[2024云南]如图,是的直径,点,在上.若, ,则的度数为( )
A. B. C. D.
2.[2024甘肃]如图,点,,在上,,垂足为.若 ,则的度数为( )
A. B. C. D.
3.[2024牡丹江]如图,四边形是的内接四边形,是的直径.若 ,则的度数为( )
A. B. C. D.
4.[2023鞍山]如图,,为的两条弦,,分别为,的中点,的半径为2.若 ,则的长为( )
A.2 B. C. D.
5.如图,,,是上的三点,且四边形是平行四边形,交于点,则的度数为( )
A. B. C. D.
二、填空题(每小题6分,共30分)
6.[2024枣庄]如图,是的内接三角形.若, ,则_ _ _ _ _ _ .
7.[2023南充]如图,是的直径,,分别是弦和的中点,若,,则的长是_ _ .
8.如图,,,,四点均在上, ,,则_ _ _ _ _ _ _ _ _ _ _ _ .
9.如图,经过五边形的四个顶点.若 , , ,则_ _ _ _ _ _ _ _ .
10.如图,是的外接圆,是的直径,,的平分线交于点,交于点,连接.若,则的长为_ _ _ _ _ _ _ _ .
三、解答题(共40分)
11.(10分)如图,在中,,以为直径作,交边于点,交的延长线于点,连接,.
(1) 求证:;
(2) 若,,求的长.
12.(15分)如图是某蔬菜基地搭建的一座圆弧形蔬菜棚的示意图,跨度,拱高(为的中点,为的中点).
(1) 求该圆弧所在圆的半径;
(2) 在距蔬菜棚的一端处竖立支撑杆,求支撑杆的高度.
13.(15分)如图,四边形是的内接四边形,,,垂足分别是,.
(1) 写出与的数量关系,并证明你的结论;
(2) 若,,求的半径.
一、选择题(每小题6分,共30分)
1.B 2.A 3.B 4.D 5.B
二、填空题(每小题6分,共30分)
6.
7.4
8.
9.
10.
三、解答题(共40分)
11.(1) 证明:是的直径,
,.
又,.
(2) 解:,,
,.
,,
.
是的直径, ,
,
.
12.(1) 解:为的中点,于点,
.
设所在的圆心为点,延长经过点,如答图.
第12题答图
设的半径为.
在中,,
,解得,
即该圆弧所在圆的半径为.
(2) 如答图,连接,过点作,交的延长线于点,
则.
在中,.
,
.
13.(1) 解:结论:.
证明:如答图,连接并延长交于点,连接.
,.
,
是的中位线,
.
是的直径, ,
.
, ,
.
,,
所对弧上的圆心角等于所对弧上的圆心角,
,.
第13题答图
(2) 由(1),得.
在中,,
,
的半径为.
同课章节目录
