24.1.3 弧、弦、圆心角 分层训练(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 24.1.3 弧、弦、圆心角 分层训练(含答案) 2025-2026学年数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 125.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 14:02:27 | ||
图片预览

文档简介
24.1.3 弧、弦、圆心角
A组·基础达标 逐点击破
知识点1 圆心角的概念及其计算
1.如图,已知为的直径,为半圆周上的一点,且所对圆心角的度数是所对圆心角度数的2倍,则圆心角 .
2.已知的半径为,弦的长为,则弦所对的圆心角 .
知识点2 弧、弦、圆心角之间的关系
3.下列说法正确的是( )
A.相等的圆心角所对的弦相等
B.相等的圆心角所对的弧相等
C.在同一个圆中,相等的弧所对的弦相等
D.相等的弦所对的圆心角相等
4.如图,在中,是的中点, ,则的度数是( )
第4题图
A. B. C. D.
5.[2022金华模拟]如图,,,,是上的四个点,且,,,垂足分别为,,则下列结论错误的是( )
第5题图
A. B.
C. D.
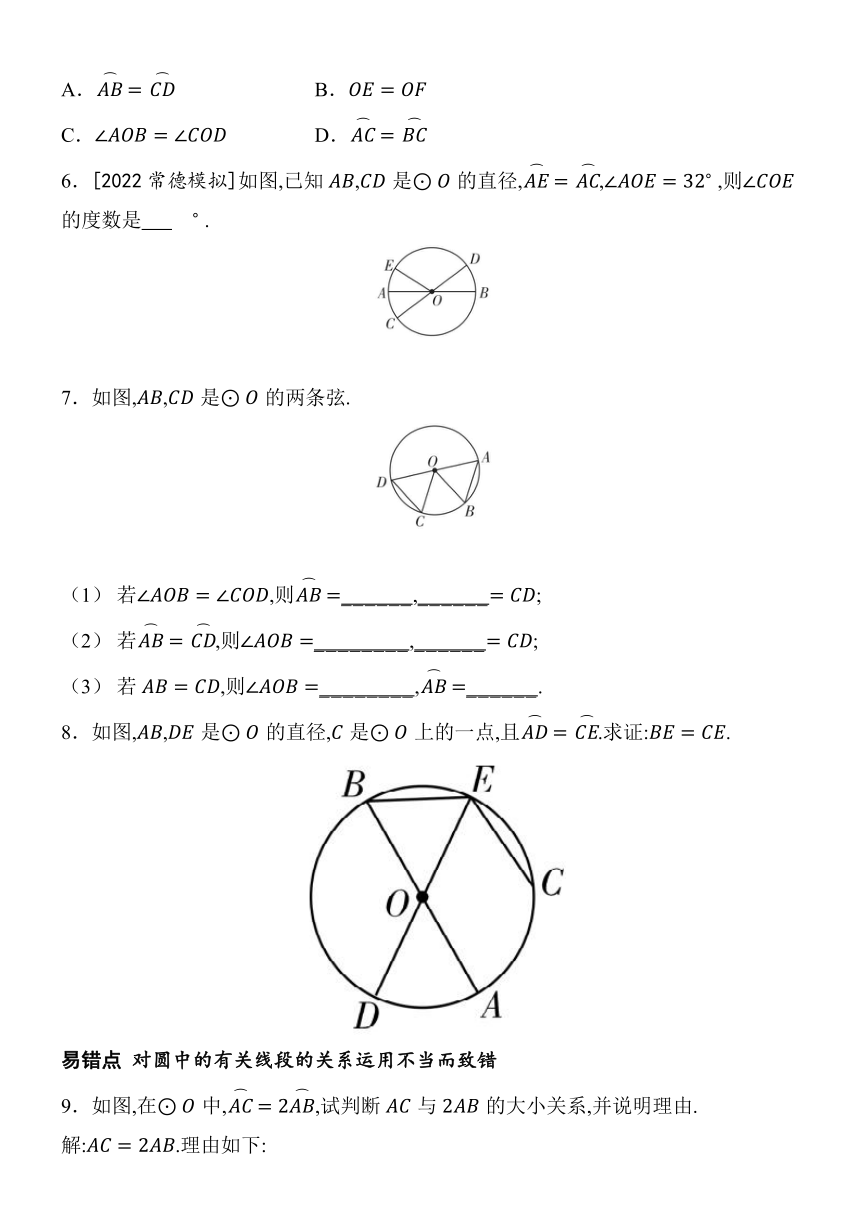
6.[2022常德模拟]如图,已知,是的直径,, ,则的度数是 .
7.如图,,是的两条弦.
(1) 若,则_ _ _ _ _ _ ,_ _ _ _ _ _ ;
(2) 若,则_ _ _ _ _ _ _ _ ,_ _ _ _ _ _ ;
(3) 若,则_ _ _ _ _ _ _ _ ,_ _ _ _ _ _ .
8.如图,,是的直径,是上的一点,且.求证:.
易错点 对圆中的有关线段的关系运用不当而致错
9.如图,在中,,试判断与的大小关系,并说明理由.
解:.理由如下:
在同圆或等圆中,同弧或等弧所对的弦相等,
当时,.
以上解答是否正确?若不正确,请改正.
B组·能力提升 强化突破
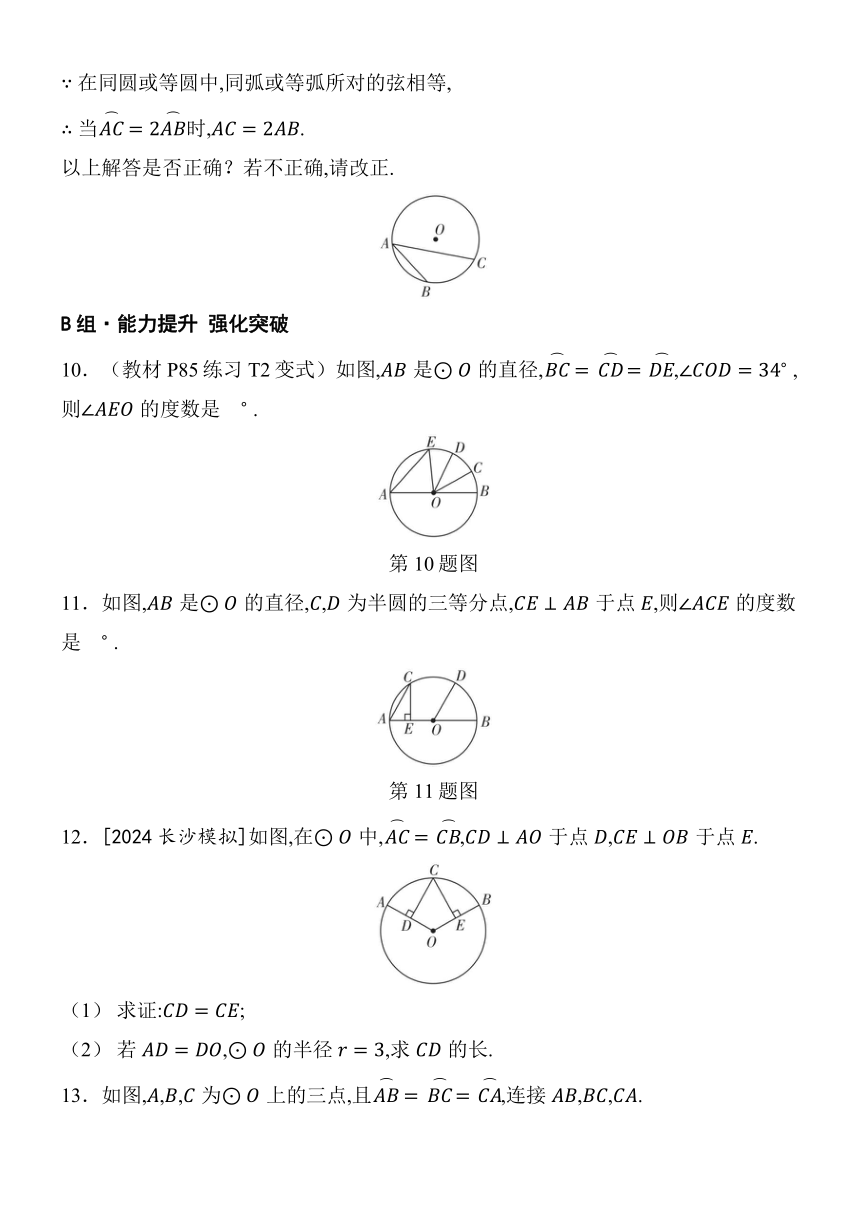
10.(教材P85练习T2变式)如图,是的直径,, ,则的度数是 .
第10题图
11.如图,是的直径,,为半圆的三等分点,于点,则的度数是 .
第11题图
12.[2024长沙模拟]如图,在中,,于点,于点.
(1) 求证:;
(2) 若,的半径,求的长.
13.如图,,,为上的三点,且,连接,,.
(1) 试确定的形状;
(2) 若,求的半径(结果用含的代数式表示).
C组·核心素养拓展 素养渗透
14.【推理能力】如图,是半圆上的一个三等分点,是的中点,是直径上的一动点,的半径为1,则的最小值为_ _ _ _ .
24.1.3 弧、弦、圆心角
A组·基础达标 逐点击破
知识点1 圆心角的概念及其计算
1.60
2.60
知识点2 弧、弦、圆心角之间的关系
3.C 4.A 5.D
6.64
7.(1) ;
(2) ;
(3) ;
8.证明:,是的直径,
,.
,,
.
易错点 对圆中的有关线段的关系运用不当而致错
9.解:不正确.
.理由如下:
如答图,连接.
第9题答图
,,
.
,.
B组·能力提升 强化突破
10.51
11.30
12.(1) 证明:如答图,连接.
第12题答图
,
.
又,,
.
(2) 解:,,
.
,
.
13.(1) 解:,
,
为等边三角形.
(2) 如答图,连接,,,过点作,垂足为.
第13题答图
,
.
又,,
,
,
,
.
由勾股定理,得,
,
解得(负值已舍).
即的半径为.
C组·核心素养拓展 素养渗透
14.
A组·基础达标 逐点击破
知识点1 圆心角的概念及其计算
1.如图,已知为的直径,为半圆周上的一点,且所对圆心角的度数是所对圆心角度数的2倍,则圆心角 .
2.已知的半径为,弦的长为,则弦所对的圆心角 .
知识点2 弧、弦、圆心角之间的关系
3.下列说法正确的是( )
A.相等的圆心角所对的弦相等
B.相等的圆心角所对的弧相等
C.在同一个圆中,相等的弧所对的弦相等
D.相等的弦所对的圆心角相等
4.如图,在中,是的中点, ,则的度数是( )
第4题图
A. B. C. D.
5.[2022金华模拟]如图,,,,是上的四个点,且,,,垂足分别为,,则下列结论错误的是( )
第5题图
A. B.
C. D.
6.[2022常德模拟]如图,已知,是的直径,, ,则的度数是 .
7.如图,,是的两条弦.
(1) 若,则_ _ _ _ _ _ ,_ _ _ _ _ _ ;
(2) 若,则_ _ _ _ _ _ _ _ ,_ _ _ _ _ _ ;
(3) 若,则_ _ _ _ _ _ _ _ ,_ _ _ _ _ _ .
8.如图,,是的直径,是上的一点,且.求证:.
易错点 对圆中的有关线段的关系运用不当而致错
9.如图,在中,,试判断与的大小关系,并说明理由.
解:.理由如下:
在同圆或等圆中,同弧或等弧所对的弦相等,
当时,.
以上解答是否正确?若不正确,请改正.
B组·能力提升 强化突破
10.(教材P85练习T2变式)如图,是的直径,, ,则的度数是 .
第10题图
11.如图,是的直径,,为半圆的三等分点,于点,则的度数是 .
第11题图
12.[2024长沙模拟]如图,在中,,于点,于点.
(1) 求证:;
(2) 若,的半径,求的长.
13.如图,,,为上的三点,且,连接,,.
(1) 试确定的形状;
(2) 若,求的半径(结果用含的代数式表示).
C组·核心素养拓展 素养渗透
14.【推理能力】如图,是半圆上的一个三等分点,是的中点,是直径上的一动点,的半径为1,则的最小值为_ _ _ _ .
24.1.3 弧、弦、圆心角
A组·基础达标 逐点击破
知识点1 圆心角的概念及其计算
1.60
2.60
知识点2 弧、弦、圆心角之间的关系
3.C 4.A 5.D
6.64
7.(1) ;
(2) ;
(3) ;
8.证明:,是的直径,
,.
,,
.
易错点 对圆中的有关线段的关系运用不当而致错
9.解:不正确.
.理由如下:
如答图,连接.
第9题答图
,,
.
,.
B组·能力提升 强化突破
10.51
11.30
12.(1) 证明:如答图,连接.
第12题答图
,
.
又,,
.
(2) 解:,,
.
,
.
13.(1) 解:,
,
为等边三角形.
(2) 如答图,连接,,,过点作,垂足为.
第13题答图
,
.
又,,
,
,
,
.
由勾股定理,得,
,
解得(负值已舍).
即的半径为.
C组·核心素养拓展 素养渗透
14.
同课章节目录
