24.3 正多边形和圆 分层训练(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 24.3 正多边形和圆 分层训练(含答案) 2025-2026学年数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 152.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 14:27:28 | ||
图片预览


文档简介
24.3 正多边形和圆
A组·基础达标 逐点击破
知识点1 正多边形与圆的关系
1.线段以点为旋转中心,逆时针旋转 ,得到,再将以点为旋转中心逆时针旋转 得到,依次操作直到点与点重合为止,顺次连接点,, ,,形成的多边形是( )
A.正四边形 B.正五边形 C.正六边形 D.正七边形
知识点2 与正多边形有关的计算
2.如果一个多边形的中心角为 ,那么这个正多边形的边数是( )
A.4 B.5 C.6 D.7
3.[2024长沙模拟]如图,正六边形内接于,若的面积等于 ,则正六边形的边长为( )
A. B.3 C.6 D.9
4.[2023衡阳]如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是.
5.如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度,则螺帽边长_ _ _ _ .
6.如图,正五边形和正三角形都是的内接多边形,则 .
知识点3 画正多边形
7.如图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图②,是的直径,请用直尺和圆规作的内接正八边形(不写作法,保留作图痕迹).
易错点 考虑问题不全面导致漏解
8.若是内接正五边形的一边,是的内接正六边形的一边,则的度数是_ _ _ _ _ _ .
B组·能力提升 强化突破
9.[2024盐城模拟]刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若的半径为2,则这个圆内接正十二边形的面积为( )
A.3 B.12 C. D.
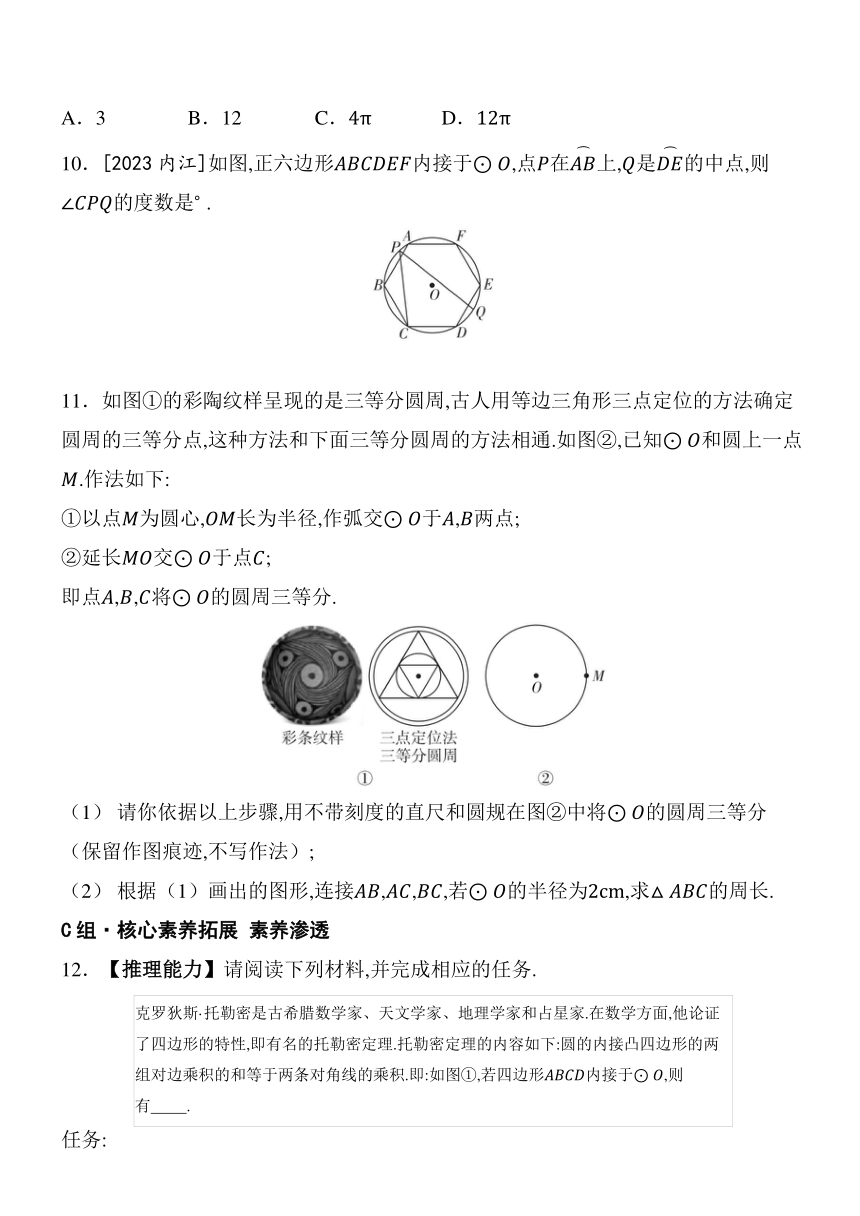
10.[2023内江]如图,正六边形内接于,点在上,是的中点,则的度数是 .
11.如图①的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图②,已知和圆上一点.作法如下:
①以点为圆心,长为半径,作弧交于,两点;
②延长交于点;
即点,,将的圆周三等分.
(1) 请你依据以上步骤,用不带刻度的直尺和圆规在图②中将的圆周三等分(保留作图痕迹,不写作法);
(2) 根据(1)画出的图形,连接,,,若的半径为,求的周长.
C组·核心素养拓展 素养渗透
12.【推理能力】请阅读下列材料,并完成相应的任务.
克罗狄斯·托勒密是古希腊数学家、天文学家、地理学家和占星家.在数学方面,他论证了四边形的特性,即有名的托勒密定理.托勒密定理的内容如下:圆的内接凸四边形的两组对边乘积的和等于两条对角线的乘积.即:如图①,若四边形内接于,则有 .
任务:
(1) 材料中划横线部分应填写的内容为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ;
(2) 如图②,正五边形内接于,,求对角线的长.
②
24.3 正多边形和圆
A组·基础达标 逐点击破
知识点1 正多边形与圆的关系
1.C
知识点2 与正多边形有关的计算
2.B 3.B
4.10
5.
6.48
知识点3 画正多边形
7.解:作图如答图.
第7题答图
易错点 考虑问题不全面导致漏解
8.6或114
B组·能力提升 强化突破
9.B
10.45
11.(1) 解:如答图,点,,即为所求作.
第11题答图
(2) 如答图,设交于点.
,
, .
,
.
, .
,,
,
,
的周长为.
C组·核心素养拓展 素养渗透
12.(1)
(2) 解:如答图,连接,.
第12题答图
五边形是正五边形,
,
设.
在圆内接四边形中,
由托勒密定理,
得,
即,
解得,(舍去).
对角线的长为.
A组·基础达标 逐点击破
知识点1 正多边形与圆的关系
1.线段以点为旋转中心,逆时针旋转 ,得到,再将以点为旋转中心逆时针旋转 得到,依次操作直到点与点重合为止,顺次连接点,, ,,形成的多边形是( )
A.正四边形 B.正五边形 C.正六边形 D.正七边形
知识点2 与正多边形有关的计算
2.如果一个多边形的中心角为 ,那么这个正多边形的边数是( )
A.4 B.5 C.6 D.7
3.[2024长沙模拟]如图,正六边形内接于,若的面积等于 ,则正六边形的边长为( )
A. B.3 C.6 D.9
4.[2023衡阳]如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是.
5.如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度,则螺帽边长_ _ _ _ .
6.如图,正五边形和正三角形都是的内接多边形,则 .
知识点3 画正多边形
7.如图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图②,是的直径,请用直尺和圆规作的内接正八边形(不写作法,保留作图痕迹).
易错点 考虑问题不全面导致漏解
8.若是内接正五边形的一边,是的内接正六边形的一边,则的度数是_ _ _ _ _ _ .
B组·能力提升 强化突破
9.[2024盐城模拟]刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若的半径为2,则这个圆内接正十二边形的面积为( )
A.3 B.12 C. D.
10.[2023内江]如图,正六边形内接于,点在上,是的中点,则的度数是 .
11.如图①的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图②,已知和圆上一点.作法如下:
①以点为圆心,长为半径,作弧交于,两点;
②延长交于点;
即点,,将的圆周三等分.
(1) 请你依据以上步骤,用不带刻度的直尺和圆规在图②中将的圆周三等分(保留作图痕迹,不写作法);
(2) 根据(1)画出的图形,连接,,,若的半径为,求的周长.
C组·核心素养拓展 素养渗透
12.【推理能力】请阅读下列材料,并完成相应的任务.
克罗狄斯·托勒密是古希腊数学家、天文学家、地理学家和占星家.在数学方面,他论证了四边形的特性,即有名的托勒密定理.托勒密定理的内容如下:圆的内接凸四边形的两组对边乘积的和等于两条对角线的乘积.即:如图①,若四边形内接于,则有 .
任务:
(1) 材料中划横线部分应填写的内容为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ;
(2) 如图②,正五边形内接于,,求对角线的长.
②
24.3 正多边形和圆
A组·基础达标 逐点击破
知识点1 正多边形与圆的关系
1.C
知识点2 与正多边形有关的计算
2.B 3.B
4.10
5.
6.48
知识点3 画正多边形
7.解:作图如答图.
第7题答图
易错点 考虑问题不全面导致漏解
8.6或114
B组·能力提升 强化突破
9.B
10.45
11.(1) 解:如答图,点,,即为所求作.
第11题答图
(2) 如答图,设交于点.
,
, .
,
.
, .
,,
,
,
的周长为.
C组·核心素养拓展 素养渗透
12.(1)
(2) 解:如答图,连接,.
第12题答图
五边形是正五边形,
,
设.
在圆内接四边形中,
由托勒密定理,
得,
即,
解得,(舍去).
对角线的长为.
同课章节目录
