第二十三章 旋转 本章复习课(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 第二十三章 旋转 本章复习课(含答案) 2025-2026学年数学人教版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 178.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 00:00:00 | ||
图片预览



文档简介
第二十三章 旋转 本章复习课
整合提升 练就四能
类型之1 中心对称图形与轴对称图形
1.随着我国航天领域的快速发展,从“天宫一号”发射升空,到天和核心舱归位,我国正式迈入了“空间站时代”.下面有关我国航天领域的图标中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.数学世界奇妙无穷,其中曲线是微分几何的研究对象之一.下列数学曲线是中心对称图形的是( )
A. B.
C. D.
类型之2 旋转的性质
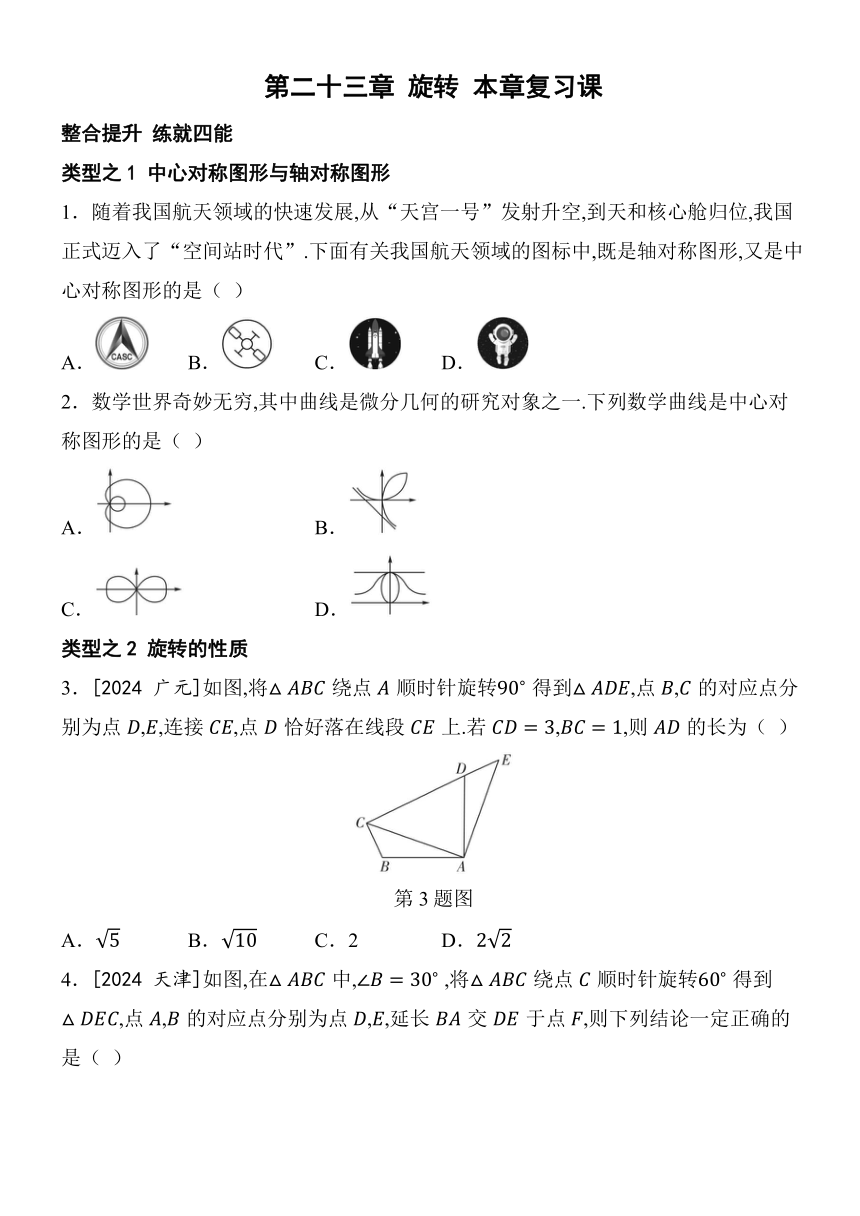
3.[2024 广元]如图,将绕点顺时针旋转 得到,点,的对应点分别为点,,连接,点恰好落在线段上.若,,则的长为( )
第3题图
A. B. C.2 D.
4.[2024 天津]如图,在中, ,将绕点顺时针旋转 得到,点,的对应点分别为点,,延长交于点,则下列结论一定正确的是( )
第4题图
A. B.
C. D.
类型之3 关于原点对称的点的坐标
5.[2024 长沙模拟]点与点关于原点对称,则_ _ _ _ _ _ .
类型之4 坐标系中的旋转及旋转作图
6.[2024 长沙模拟]按照要求画图:
(1) 如图①,在平面直角坐标系中,将绕原点顺时针旋转 得到,点,,的对应点分别为点,,.画出旋转后的.
(2) 如图②,下列网格都是由9个相同小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形(画出两种即可).
类型之5 旋转证明
7.如图,将矩形绕点顺时针旋转,得到矩形,点的对应点恰好落在的延长线上,边交边于点.
(1) 求证:;
(2) 若,,求的长.
素养专练 培养三会
8.【创新意识】数学课上,老师提出了这样一个问题:如图①,是正方形内一点,,,,你能求出的度数吗?小明通过观察、分析、思考,形成了如下思路:将绕点逆时针旋转 ,得到,连接,求出的度数.
①
(1) 请参考小明的思路,写出完整的解答过程.
(2) 如图②,若是正方形外一点,,,,求的度数.
②
本章复习课
整合提升 练就四能
类型之1 中心对称图形与轴对称图形
1.B 2.C
类型之2 旋转的性质
3.A 4.D
类型之3 关于原点对称的点的坐标
5.
类型之4 坐标系中的旋转及旋转作图
6.(1) 解:如答图①所示.
(2) (答案不唯一)如答图②所示.
类型之5 旋转证明
7.(1) 证明:如答图,连接,.
第7题答图
将矩形绕点顺时针旋转,得到矩形,
.
四边形为矩形,
,即.
.
(2) 解:将矩形绕点顺时针旋转,得到矩形,
, .
,
,
.
设,则.
由勾股定理,得,
,
解得,
的长为.
素养专练 培养三会
8.(1) 解:如答图①,将绕点逆时针旋转 ,得到,连接.
第8题答图①
, ,
, .
又,,
,
是直角三角形,且 ,
.
(2) 如答图②,将绕点逆时针旋转 ,得到,连接.
第8题答图②
, ,
, .
又,,
,
是直角三角形,且 ,
.
整合提升 练就四能
类型之1 中心对称图形与轴对称图形
1.随着我国航天领域的快速发展,从“天宫一号”发射升空,到天和核心舱归位,我国正式迈入了“空间站时代”.下面有关我国航天领域的图标中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.数学世界奇妙无穷,其中曲线是微分几何的研究对象之一.下列数学曲线是中心对称图形的是( )
A. B.
C. D.
类型之2 旋转的性质
3.[2024 广元]如图,将绕点顺时针旋转 得到,点,的对应点分别为点,,连接,点恰好落在线段上.若,,则的长为( )
第3题图
A. B. C.2 D.
4.[2024 天津]如图,在中, ,将绕点顺时针旋转 得到,点,的对应点分别为点,,延长交于点,则下列结论一定正确的是( )
第4题图
A. B.
C. D.
类型之3 关于原点对称的点的坐标
5.[2024 长沙模拟]点与点关于原点对称,则_ _ _ _ _ _ .
类型之4 坐标系中的旋转及旋转作图
6.[2024 长沙模拟]按照要求画图:
(1) 如图①,在平面直角坐标系中,将绕原点顺时针旋转 得到,点,,的对应点分别为点,,.画出旋转后的.
(2) 如图②,下列网格都是由9个相同小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形(画出两种即可).
类型之5 旋转证明
7.如图,将矩形绕点顺时针旋转,得到矩形,点的对应点恰好落在的延长线上,边交边于点.
(1) 求证:;
(2) 若,,求的长.
素养专练 培养三会
8.【创新意识】数学课上,老师提出了这样一个问题:如图①,是正方形内一点,,,,你能求出的度数吗?小明通过观察、分析、思考,形成了如下思路:将绕点逆时针旋转 ,得到,连接,求出的度数.
①
(1) 请参考小明的思路,写出完整的解答过程.
(2) 如图②,若是正方形外一点,,,,求的度数.
②
本章复习课
整合提升 练就四能
类型之1 中心对称图形与轴对称图形
1.B 2.C
类型之2 旋转的性质
3.A 4.D
类型之3 关于原点对称的点的坐标
5.
类型之4 坐标系中的旋转及旋转作图
6.(1) 解:如答图①所示.
(2) (答案不唯一)如答图②所示.
类型之5 旋转证明
7.(1) 证明:如答图,连接,.
第7题答图
将矩形绕点顺时针旋转,得到矩形,
.
四边形为矩形,
,即.
.
(2) 解:将矩形绕点顺时针旋转,得到矩形,
, .
,
,
.
设,则.
由勾股定理,得,
,
解得,
的长为.
素养专练 培养三会
8.(1) 解:如答图①,将绕点逆时针旋转 ,得到,连接.
第8题答图①
, ,
, .
又,,
,
是直角三角形,且 ,
.
(2) 如答图②,将绕点逆时针旋转 ,得到,连接.
第8题答图②
, ,
, .
又,,
,
是直角三角形,且 ,
.
同课章节目录
