第二十二章 二次函数 质量评估(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 第二十二章 二次函数 质量评估(含答案) 2025-2026学年数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 14:32:57 | ||
图片预览




文档简介
第二十二章 二次函数 质量评估
[时间:120分钟 分值:120分]
一、选择题(共10个小题,每小题3分,共30分)
1.下列函数中,是关于的二次函数的是( )
A. B.
C. D.
2.抛物线的顶点坐标是( )
A. B. C. D.
3.把抛物线向左平移2个单位长度,再向上平移5个单位长度,得到的抛物线的解析式为( )
A. B.
C. D.
4.已知点,是抛物线上关于对称轴对称的两点,若点的横坐标为,则点的横坐标为( )
A.5 B.4 C.3 D.2
5.关于二次函数的图象与性质的说法中,正确的是( )
A.图象的开口向下 B.图象的对称轴为直线
C.函数的最小值为1 D.当时,随的增大而增大
6.关于的一元二次方程有两个相等的实数根,则二次函数的图象与轴的交点情况是( )
A.没有交点 B.有一个交点
C.有两个交点 D.不能确定
7.已知二次函数,当时,的取值范围是( )
A. B.
C. D.
8.二次函数的图象如图所示,则一次函数在直角坐标系中的大致图象是( )
A. B.
C. D.
9.将进货价格为每个35元的商品按每个40元售出时,能卖出200个.已知该商品单价每上涨1元,其销售量就减少5个.设这种商品的售价上涨元时,获得的利润为元,则下列关系式正确的是( )
A. B.
C. D.
10.已知二次函数的图象与轴的一个交点坐标为,对称轴为直线,有下列结论:;②若点,,均在该二次函数图象上,则;③若为任意实数,则;④方程的两实数根为,,且,则,.其中正确结论的序号为( )
A.①②③ B.①③④ C.②③④ D.①④
二、填空题(共6个小题,每小题3分,共18分)
11.请写出一个函数解析式,使其图象的对称轴为轴:_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
12.抛物线与轴的交点坐标是_ _ _ _ _ _ _ _ .
13.二次函数的最大值是_ _ _ _ _ _ .
14.二次函数的图象与轴有两个不同的交点,则的值可以为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
15.已知点,,都在二次函数的图象上,则,,的大小关系是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ (用“ ”连接).
16.如图,抛物线与轴相交于点,,与轴相交于点,点在抛物线上,当轴时,_ _ _ _ _ _ _ _ .
三、解答题(共9个题,共72分)
17.(6分)通过配方,写出下列抛物线的开口方向、对称轴和顶点坐标.
(1) ;
(2) .
18.(6分)已知函数是关于的二次函数.
(1) 求满足条件的的值;
(2) 判断点是否在该二次函数的图象上.
19.(6分)如下表给出一个二次函数的一些取值情况:
… 0 1 2 …
… 3 0 0 3 …
(1) 请在所给的直角坐标系中画出这个二次函数的图象;
(2) 根据图象说明:当取何值时,的值小于0?
20.(8分)已知二次函数.
(1) 求证:无论为何实数,此二次函数的图象与轴都有两个不同的交点;
(2) 若此二次函数有最小值,求此二次函数的解析式.
21.(8分)如图,已知抛物线与轴交于点,,与轴交于点.
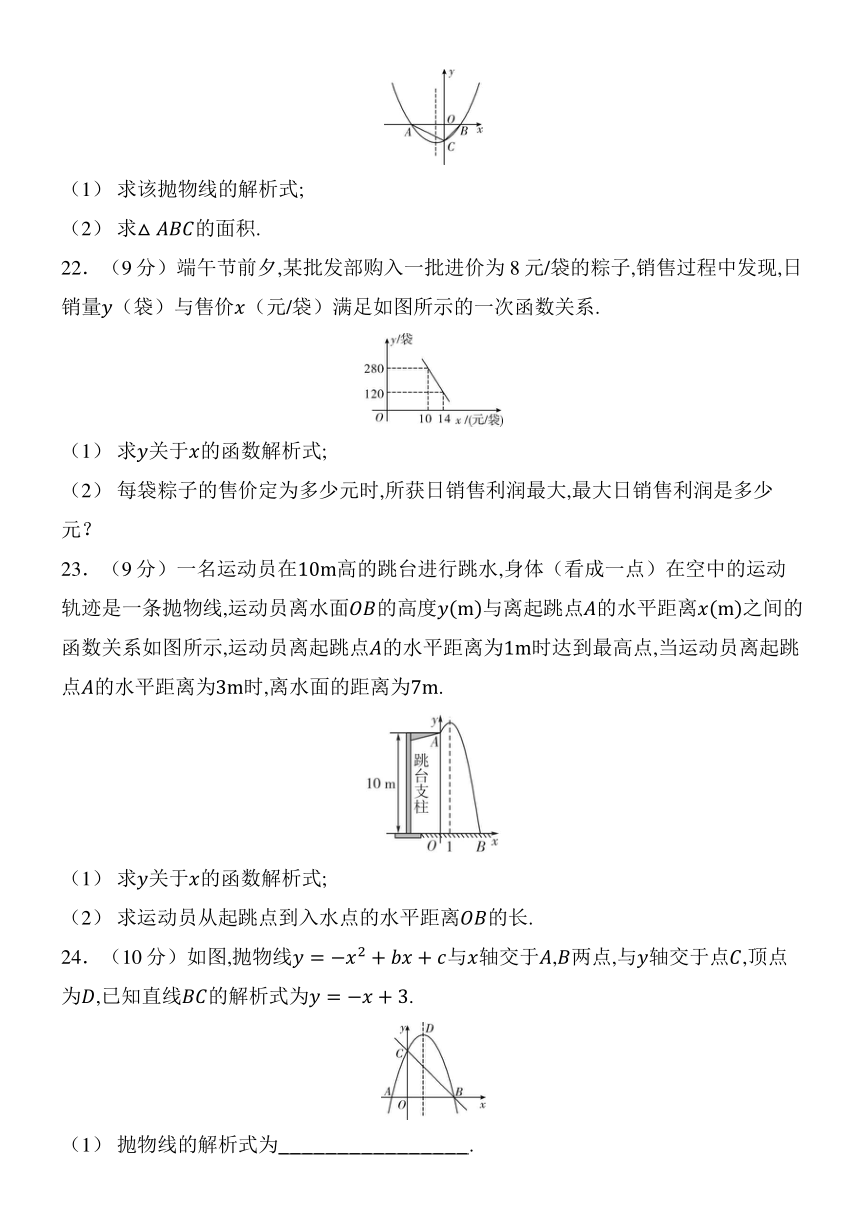
(1) 求该抛物线的解析式;
(2) 求的面积.
22.(9分)端午节前夕,某批发部购入一批进价为8元/袋的粽子,销售过程中发现,日销量(袋)与售价(元/袋)满足如图所示的一次函数关系.
(1) 求关于的函数解析式;
(2) 每袋粽子的售价定为多少元时,所获日销售利润最大,最大日销售利润是多少元?
23.(9分)一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点的水平距离之间的函数关系如图所示,运动员离起跳点的水平距离为时达到最高点,当运动员离起跳点的水平距离为时,离水面的距离为.
(1) 求关于的函数解析式;
(2) 求运动员从起跳点到入水点的水平距离的长.
24.(10分)如图,抛物线与轴交于,两点,与轴交于点,顶点为,已知直线的解析式为.
(1) 抛物线的解析式为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
(2) 求点到直线的距离.
(3) 在抛物线的对称轴上是否存在一点,使得是等腰三角形?若存在,求出点的坐标;若不存在,请说明理由.
25.(10分)定义:函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“阶方点”.例如,点,是函数图象的“阶方点”;点是函数图象的“1阶方点”.
(1) 在;;,三点中,是正比例函数图象的“1阶方点”的有(填序号);
(2) 若关于的一次函数图象的“2阶方点”有且只有一个,求的值;
(3) 若函数图象恰好经过“阶方点”中的点,则点称为此函数图象的“不动阶方点”,若关于的二次函数的图象上存在唯一的一个“不动阶方点”,且当时,的最小值为,求的值.
第二十二章质量评估
一、选择题(共10个小题,每小题3分,共30分)
1.B 2.B 3.C 4.D 5.C 6.B 7.A 8.D 9.C 10.B
二、填空题(共6个小题,每小题3分,共18分)
11.(答案不唯一)
12.
13.
14.(答案不唯一)
15.
16.
三、解答题(共9个题,共72分)
17.(1) 解:,
抛物线的开口向上,对称轴为直线,
顶点坐标为.
(2) ,
抛物线的开口向下,对称轴为直线,
顶点坐标为,.
18.(1) 解:由题意,得
解得.
(2) 由(1)知函数解析式为.
当时,,
点不在该二次函数的图象上.
19.(1) 解:画出图象如答图所示.
第19题答图
(2) 由函数图象可知,当时,.
20.(1) 证明:.
,,
无论为何实数,此二次函数的图象与轴都有两个不同的交点.
(2) 解:由题意,得,
整理,得,解得,
此二次函数的解析式为.
21.(1) 解: 抛物线过点,,
解得
该抛物线的解析式为.
(2) 令,则,,.
,,,,
.
.
22.(1) 解:设关于的函数解析式为.
把点,分别代入,
得解得
关于的函数解析式为.
(2) 设日销售利润为元.
则.
,抛物线的开口向下,
当时,有最大值,最大值为810.
答:当粽子的售价定为12.5元/袋时,日销售利润最大,最大日销售利润是810元.
23.(1) 解:由题意,得抛物线过和,对称轴为直线.
设关于的函数解析式为,
解得
关于的函数解析式为,
即.
(2) 在中,
令,得,
解得或(舍去),
运动员从起跳点到入水点的水平距离的长为.
24.(1)
(2) 解:,.
易知,,
,,.
,是直角三角形, ,
点到直线的距离为线段的长,
即点到直线的距离为.
(3) 存在点,使得是等腰三角形.理由如下:
,
抛物线的对称轴为直线.
设,,,
,,.
当时,,解得,
;
当时,,解得或(舍去),
;
当时,,解得或,
或.
综上所述,点的坐标为或或或.
25.(1) ②③
(2) 解:,
函数经过定点.
如答图①②,在以点为中心,边长为4的正方形中,当直线与正方形区域只有唯一交点时,图象的“2阶方点”有且只有一个.
第25题答图① 第25题答图②
由答图可知,,.
一次函数图象的“2阶方点”有且只有一个,
当直线经过点时,,
解得,此时图象的“2阶方点”有且只有一个;
当直线经过点时,,
解得,此时图象的“2阶方点”有且只有一个.
综上所述,的值为3或.
(3) 点在直线上,
当的图象上存在唯一的一个“不动阶方点”时,方程有两个相等的实数根,
,
,
当时,的最小值为,
当时,,取得最小值,则,
解得,不符合题意.
当时,此时,取最小值,即,
解得(舍去)或.
当时,此时,取最小值,即,
解得(舍去)或,
综上所述,或.
[时间:120分钟 分值:120分]
一、选择题(共10个小题,每小题3分,共30分)
1.下列函数中,是关于的二次函数的是( )
A. B.
C. D.
2.抛物线的顶点坐标是( )
A. B. C. D.
3.把抛物线向左平移2个单位长度,再向上平移5个单位长度,得到的抛物线的解析式为( )
A. B.
C. D.
4.已知点,是抛物线上关于对称轴对称的两点,若点的横坐标为,则点的横坐标为( )
A.5 B.4 C.3 D.2
5.关于二次函数的图象与性质的说法中,正确的是( )
A.图象的开口向下 B.图象的对称轴为直线
C.函数的最小值为1 D.当时,随的增大而增大
6.关于的一元二次方程有两个相等的实数根,则二次函数的图象与轴的交点情况是( )
A.没有交点 B.有一个交点
C.有两个交点 D.不能确定
7.已知二次函数,当时,的取值范围是( )
A. B.
C. D.
8.二次函数的图象如图所示,则一次函数在直角坐标系中的大致图象是( )
A. B.
C. D.
9.将进货价格为每个35元的商品按每个40元售出时,能卖出200个.已知该商品单价每上涨1元,其销售量就减少5个.设这种商品的售价上涨元时,获得的利润为元,则下列关系式正确的是( )
A. B.
C. D.
10.已知二次函数的图象与轴的一个交点坐标为,对称轴为直线,有下列结论:;②若点,,均在该二次函数图象上,则;③若为任意实数,则;④方程的两实数根为,,且,则,.其中正确结论的序号为( )
A.①②③ B.①③④ C.②③④ D.①④
二、填空题(共6个小题,每小题3分,共18分)
11.请写出一个函数解析式,使其图象的对称轴为轴:_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
12.抛物线与轴的交点坐标是_ _ _ _ _ _ _ _ .
13.二次函数的最大值是_ _ _ _ _ _ .
14.二次函数的图象与轴有两个不同的交点,则的值可以为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
15.已知点,,都在二次函数的图象上,则,,的大小关系是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ (用“ ”连接).
16.如图,抛物线与轴相交于点,,与轴相交于点,点在抛物线上,当轴时,_ _ _ _ _ _ _ _ .
三、解答题(共9个题,共72分)
17.(6分)通过配方,写出下列抛物线的开口方向、对称轴和顶点坐标.
(1) ;
(2) .
18.(6分)已知函数是关于的二次函数.
(1) 求满足条件的的值;
(2) 判断点是否在该二次函数的图象上.
19.(6分)如下表给出一个二次函数的一些取值情况:
… 0 1 2 …
… 3 0 0 3 …
(1) 请在所给的直角坐标系中画出这个二次函数的图象;
(2) 根据图象说明:当取何值时,的值小于0?
20.(8分)已知二次函数.
(1) 求证:无论为何实数,此二次函数的图象与轴都有两个不同的交点;
(2) 若此二次函数有最小值,求此二次函数的解析式.
21.(8分)如图,已知抛物线与轴交于点,,与轴交于点.
(1) 求该抛物线的解析式;
(2) 求的面积.
22.(9分)端午节前夕,某批发部购入一批进价为8元/袋的粽子,销售过程中发现,日销量(袋)与售价(元/袋)满足如图所示的一次函数关系.
(1) 求关于的函数解析式;
(2) 每袋粽子的售价定为多少元时,所获日销售利润最大,最大日销售利润是多少元?
23.(9分)一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点的水平距离之间的函数关系如图所示,运动员离起跳点的水平距离为时达到最高点,当运动员离起跳点的水平距离为时,离水面的距离为.
(1) 求关于的函数解析式;
(2) 求运动员从起跳点到入水点的水平距离的长.
24.(10分)如图,抛物线与轴交于,两点,与轴交于点,顶点为,已知直线的解析式为.
(1) 抛物线的解析式为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
(2) 求点到直线的距离.
(3) 在抛物线的对称轴上是否存在一点,使得是等腰三角形?若存在,求出点的坐标;若不存在,请说明理由.
25.(10分)定义:函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“阶方点”.例如,点,是函数图象的“阶方点”;点是函数图象的“1阶方点”.
(1) 在;;,三点中,是正比例函数图象的“1阶方点”的有(填序号);
(2) 若关于的一次函数图象的“2阶方点”有且只有一个,求的值;
(3) 若函数图象恰好经过“阶方点”中的点,则点称为此函数图象的“不动阶方点”,若关于的二次函数的图象上存在唯一的一个“不动阶方点”,且当时,的最小值为,求的值.
第二十二章质量评估
一、选择题(共10个小题,每小题3分,共30分)
1.B 2.B 3.C 4.D 5.C 6.B 7.A 8.D 9.C 10.B
二、填空题(共6个小题,每小题3分,共18分)
11.(答案不唯一)
12.
13.
14.(答案不唯一)
15.
16.
三、解答题(共9个题,共72分)
17.(1) 解:,
抛物线的开口向上,对称轴为直线,
顶点坐标为.
(2) ,
抛物线的开口向下,对称轴为直线,
顶点坐标为,.
18.(1) 解:由题意,得
解得.
(2) 由(1)知函数解析式为.
当时,,
点不在该二次函数的图象上.
19.(1) 解:画出图象如答图所示.
第19题答图
(2) 由函数图象可知,当时,.
20.(1) 证明:.
,,
无论为何实数,此二次函数的图象与轴都有两个不同的交点.
(2) 解:由题意,得,
整理,得,解得,
此二次函数的解析式为.
21.(1) 解: 抛物线过点,,
解得
该抛物线的解析式为.
(2) 令,则,,.
,,,,
.
.
22.(1) 解:设关于的函数解析式为.
把点,分别代入,
得解得
关于的函数解析式为.
(2) 设日销售利润为元.
则.
,抛物线的开口向下,
当时,有最大值,最大值为810.
答:当粽子的售价定为12.5元/袋时,日销售利润最大,最大日销售利润是810元.
23.(1) 解:由题意,得抛物线过和,对称轴为直线.
设关于的函数解析式为,
解得
关于的函数解析式为,
即.
(2) 在中,
令,得,
解得或(舍去),
运动员从起跳点到入水点的水平距离的长为.
24.(1)
(2) 解:,.
易知,,
,,.
,是直角三角形, ,
点到直线的距离为线段的长,
即点到直线的距离为.
(3) 存在点,使得是等腰三角形.理由如下:
,
抛物线的对称轴为直线.
设,,,
,,.
当时,,解得,
;
当时,,解得或(舍去),
;
当时,,解得或,
或.
综上所述,点的坐标为或或或.
25.(1) ②③
(2) 解:,
函数经过定点.
如答图①②,在以点为中心,边长为4的正方形中,当直线与正方形区域只有唯一交点时,图象的“2阶方点”有且只有一个.
第25题答图① 第25题答图②
由答图可知,,.
一次函数图象的“2阶方点”有且只有一个,
当直线经过点时,,
解得,此时图象的“2阶方点”有且只有一个;
当直线经过点时,,
解得,此时图象的“2阶方点”有且只有一个.
综上所述,的值为3或.
(3) 点在直线上,
当的图象上存在唯一的一个“不动阶方点”时,方程有两个相等的实数根,
,
,
当时,的最小值为,
当时,,取得最小值,则,
解得,不符合题意.
当时,此时,取最小值,即,
解得(舍去)或.
当时,此时,取最小值,即,
解得(舍去)或,
综上所述,或.
同课章节目录
