第二十四章 圆 本章复习课(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 第二十四章 圆 本章复习课(含答案) 2025-2026学年数学人教版九年级上册 | 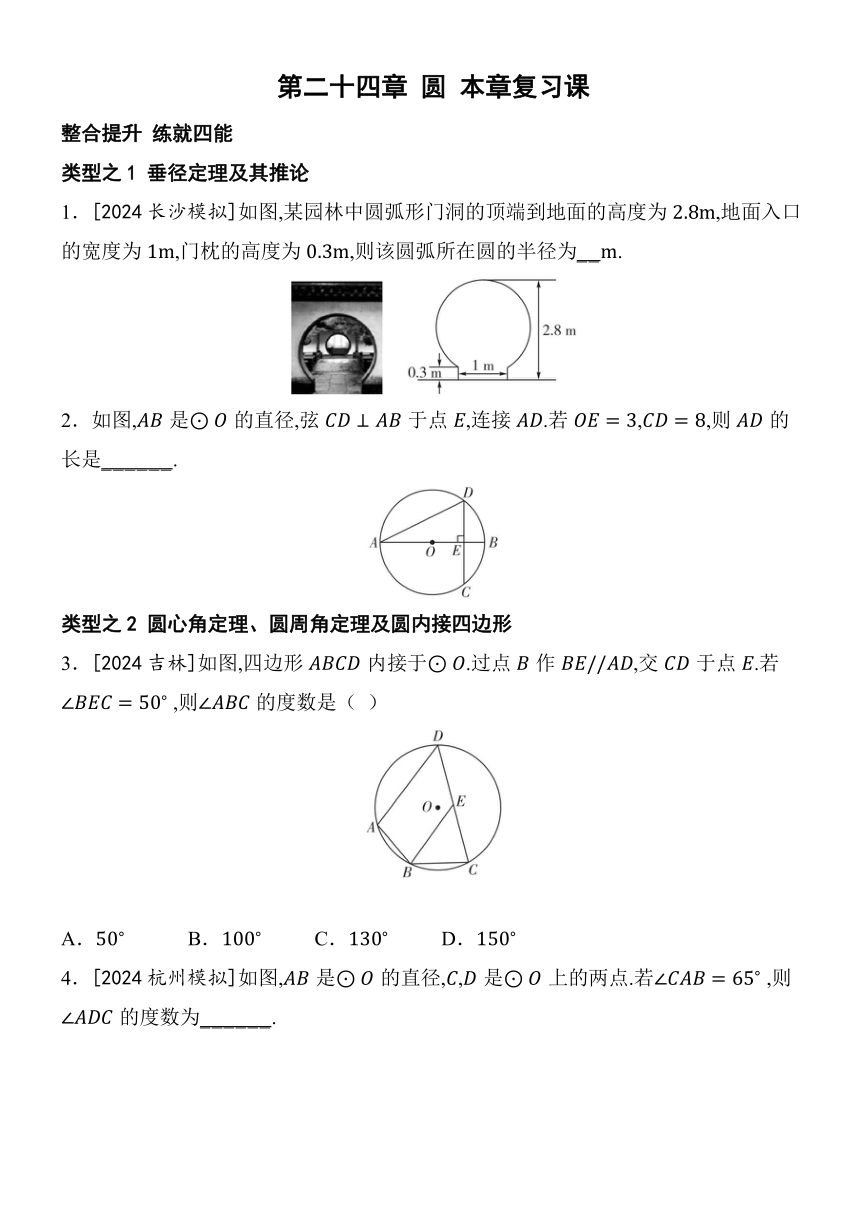 | |
| 格式 | docx | ||
| 文件大小 | 141.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 14:39:36 | ||
图片预览


文档简介
第二十四章 圆 本章复习课
整合提升 练就四能
类型之1 垂径定理及其推论
1.[2024长沙模拟]如图,某园林中圆弧形门洞的顶端到地面的高度为,地面入口的宽度为,门枕的高度为,则该圆弧所在圆的半径为_ _ .
2.如图,是的直径,弦于点,连接.若,,则的长是_ _ _ _ _ _ .
类型之2 圆心角定理、圆周角定理及圆内接四边形
3.[2024吉林]如图,四边形内接于.过点作,交于点.若 ,则的度数是( )
A. B. C. D.
4.[2024杭州模拟]如图,是的直径,,是上的两点.若 ,则的度数为_ _ _ _ _ _ .
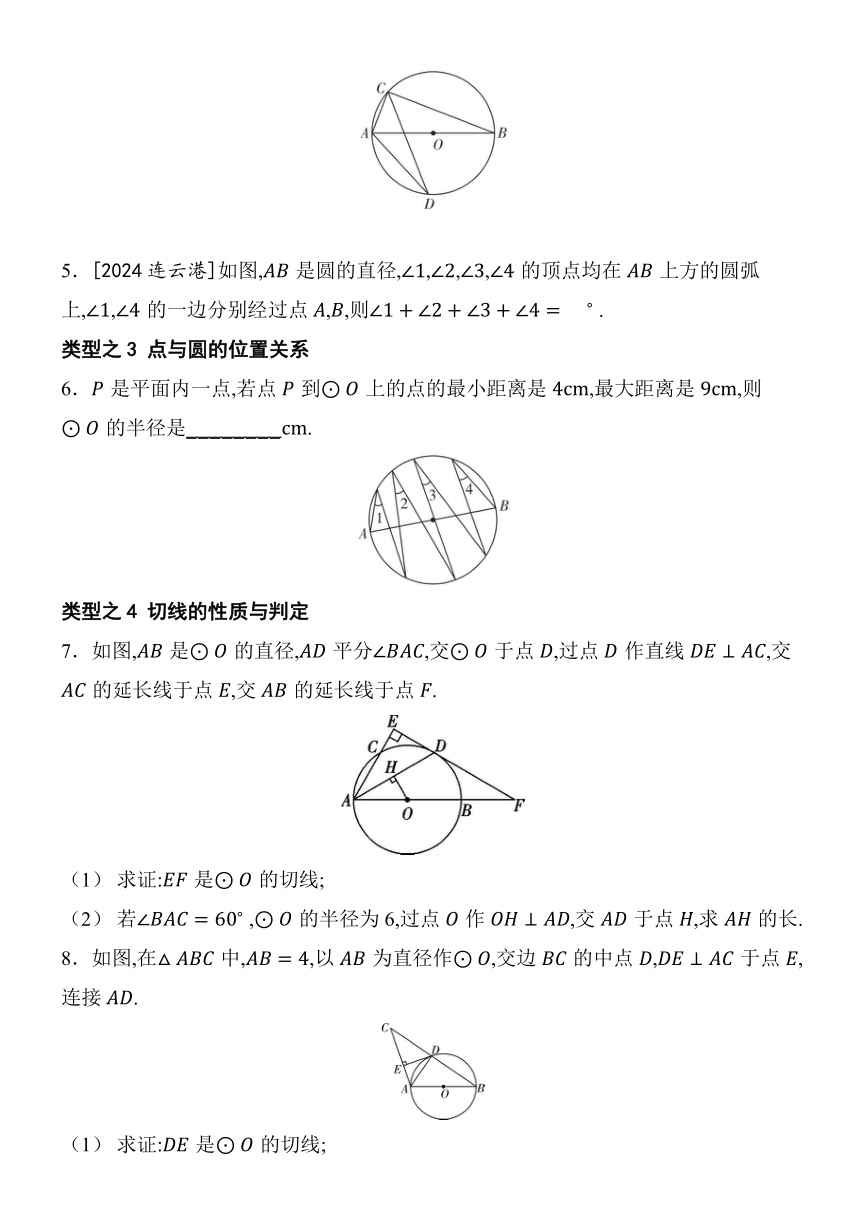
5.[2024连云港]如图,是圆的直径,,,,的顶点均在上方的圆弧上,,的一边分别经过点,,则 .
类型之3 点与圆的位置关系
6.是平面内一点,若点到上的点的最小距离是,最大距离是,则的半径是_ _ _ _ _ _ _ _ .
类型之4 切线的性质与判定
7.如图,是的直径,平分,交于点,过点作直线,交的延长线于点,交的延长线于点.
(1) 求证:是的切线;
(2) 若 ,的半径为6,过点作,交于点,求的长.
8.如图,在中,,以为直径作,交边的中点,于点,连接.
(1) 求证:是的切线;
(2) 请你给添加一个条件,并求的长.
类型之5 切线长定理与三角形的内切圆
9.[2024滨州]刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式.如图,在中, ,,,的长分别为,,,则可以用含,,的式子表示出的内切圆直径.下列表达式错误的是( )
A. B.
C. D.
类型之6 正多边形与圆
10.[2024苏州]铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点,所在圆的圆心恰好是的内心.若,则花窗的周长(图中实线部分的长度)为_ _ _ _ .(结果保留)
类型之7 弧长与扇形的面积、圆锥的侧面积和全面积
11.[2024遂宁]工人师傅在检查排污管道时发现淤泥堆积.如图,排污管道的横截面是直径为的圆,为预估淤泥量,测得淤泥横截面(图中阴影部分)宽为,请计算出淤泥横截面的面积为( )
A.()m2 B.()m2
C.()m2 D.()m2
素养专练 培养三会
12.[2023常德]【模型观念】沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,是以点为圆心,长为半径的圆弧,是弦的中点,点在上,.“会圆术”给出长的近似值的计算公式:.当, 时,_ _ _ _ _ _ _ _ _ _ .(结果保留一位小数)
本章复习课
整合提升 练就四能
类型之1 垂径定理及其推论
1.1.3
2.
类型之2 圆心角定理、圆周角定理及圆内接四边形
3.C
4.
5.90
[解析]是圆的直径,所对的弧是半圆,所对圆心角的度数为 .,,,所对的弧的和为半圆, .
类型之3 点与圆的位置关系
6.6.5或2.5
类型之4 切线的性质与判定
7.(1) 证明:如答图,连接,则,
.
平分,
,
,.
,
.
经过的半径的外端,且,
是的切线.
第7题答图
(2) 解:,平分,
.
于点, .
,,
.
8.(1) 证明:连接,如答图.
为的中点,为的中点,
为的中位线,
.
,
.
为的半径,
是的切线.
第8题答图
(2) 解:添加: .
,
,
.
的长为 .
类型之5 切线长定理与三角形的内切圆
9.D
类型之6 正多边形与圆
10.
类型之7 弧长与扇形的面积、圆锥的侧面积和全面积
11.A
素养专练 培养三会
12.
整合提升 练就四能
类型之1 垂径定理及其推论
1.[2024长沙模拟]如图,某园林中圆弧形门洞的顶端到地面的高度为,地面入口的宽度为,门枕的高度为,则该圆弧所在圆的半径为_ _ .
2.如图,是的直径,弦于点,连接.若,,则的长是_ _ _ _ _ _ .
类型之2 圆心角定理、圆周角定理及圆内接四边形
3.[2024吉林]如图,四边形内接于.过点作,交于点.若 ,则的度数是( )
A. B. C. D.
4.[2024杭州模拟]如图,是的直径,,是上的两点.若 ,则的度数为_ _ _ _ _ _ .
5.[2024连云港]如图,是圆的直径,,,,的顶点均在上方的圆弧上,,的一边分别经过点,,则 .
类型之3 点与圆的位置关系
6.是平面内一点,若点到上的点的最小距离是,最大距离是,则的半径是_ _ _ _ _ _ _ _ .
类型之4 切线的性质与判定
7.如图,是的直径,平分,交于点,过点作直线,交的延长线于点,交的延长线于点.
(1) 求证:是的切线;
(2) 若 ,的半径为6,过点作,交于点,求的长.
8.如图,在中,,以为直径作,交边的中点,于点,连接.
(1) 求证:是的切线;
(2) 请你给添加一个条件,并求的长.
类型之5 切线长定理与三角形的内切圆
9.[2024滨州]刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式.如图,在中, ,,,的长分别为,,,则可以用含,,的式子表示出的内切圆直径.下列表达式错误的是( )
A. B.
C. D.
类型之6 正多边形与圆
10.[2024苏州]铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点,所在圆的圆心恰好是的内心.若,则花窗的周长(图中实线部分的长度)为_ _ _ _ .(结果保留)
类型之7 弧长与扇形的面积、圆锥的侧面积和全面积
11.[2024遂宁]工人师傅在检查排污管道时发现淤泥堆积.如图,排污管道的横截面是直径为的圆,为预估淤泥量,测得淤泥横截面(图中阴影部分)宽为,请计算出淤泥横截面的面积为( )
A.()m2 B.()m2
C.()m2 D.()m2
素养专练 培养三会
12.[2023常德]【模型观念】沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,是以点为圆心,长为半径的圆弧,是弦的中点,点在上,.“会圆术”给出长的近似值的计算公式:.当, 时,_ _ _ _ _ _ _ _ _ _ .(结果保留一位小数)
本章复习课
整合提升 练就四能
类型之1 垂径定理及其推论
1.1.3
2.
类型之2 圆心角定理、圆周角定理及圆内接四边形
3.C
4.
5.90
[解析]是圆的直径,所对的弧是半圆,所对圆心角的度数为 .,,,所对的弧的和为半圆, .
类型之3 点与圆的位置关系
6.6.5或2.5
类型之4 切线的性质与判定
7.(1) 证明:如答图,连接,则,
.
平分,
,
,.
,
.
经过的半径的外端,且,
是的切线.
第7题答图
(2) 解:,平分,
.
于点, .
,,
.
8.(1) 证明:连接,如答图.
为的中点,为的中点,
为的中位线,
.
,
.
为的半径,
是的切线.
第8题答图
(2) 解:添加: .
,
,
.
的长为 .
类型之5 切线长定理与三角形的内切圆
9.D
类型之6 正多边形与圆
10.
类型之7 弧长与扇形的面积、圆锥的侧面积和全面积
11.A
素养专练 培养三会
12.
同课章节目录
