第二十四章 圆 质量评估(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 第二十四章 圆 质量评估(含答案) 2025-2026学年数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 229.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 14:38:30 | ||
图片预览

文档简介
第二十四章 圆 质量评估
[时间:120分钟 分值:120分]
一、选择题(共10个小题,每小题3分,共30分)
1.已知点在外,,那么的半径可能为( )
A. B. C. D.
2.如图,点,,在上,连接,,,.若 ,则的度数为( )
A. B. C. D.
3.如图,是的弦,若的半径,圆心到弦的距离,则弦的长为( )
A.4 B.6 C.8 D.10
4.如图,,是的切线,,为切点,是的直径, ,则的度数为( )
A. B. C. D.
5.如图,是的直径,,是上的两点.若 ,则的度数为( )
A. B. C. D.
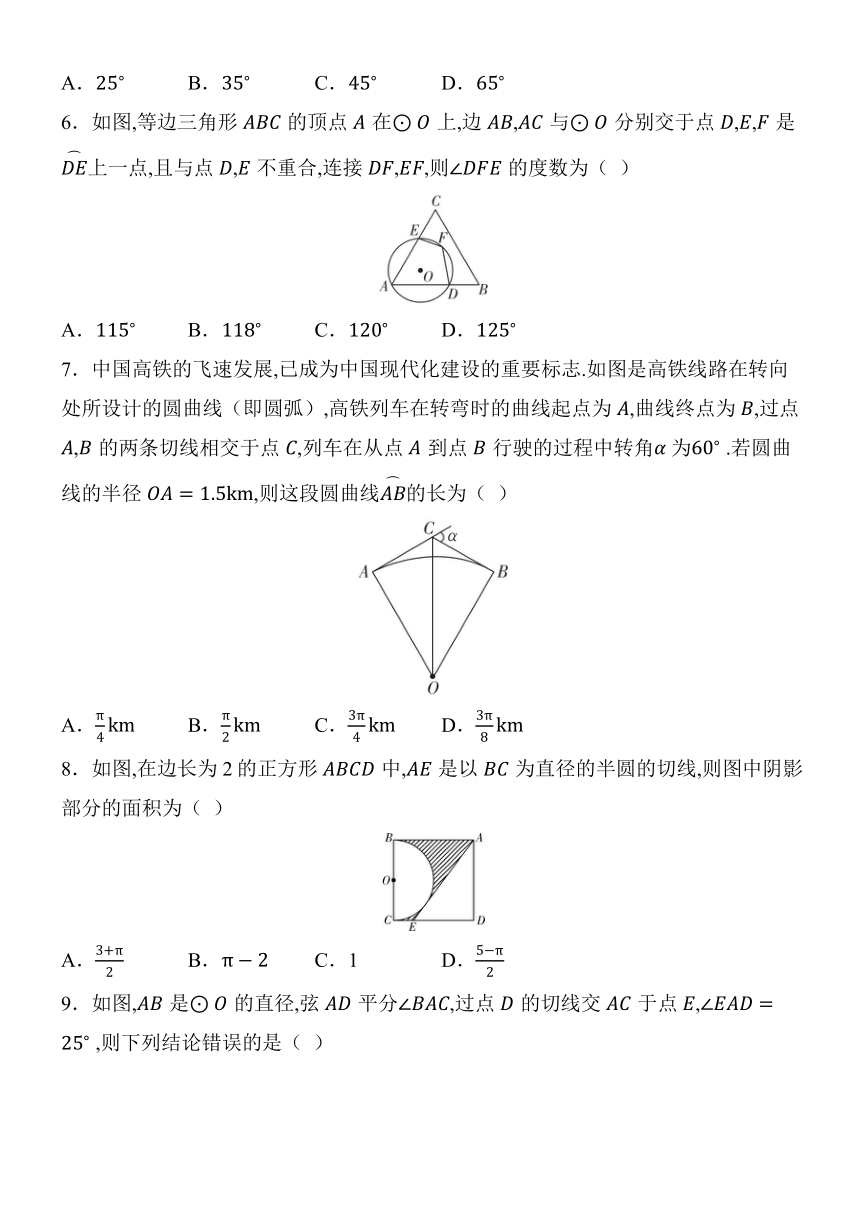
6.如图,等边三角形的顶点在上,边,与分别交于点,,是上一点,且与点,不重合,连接,,则的度数为( )
A. B. C. D.
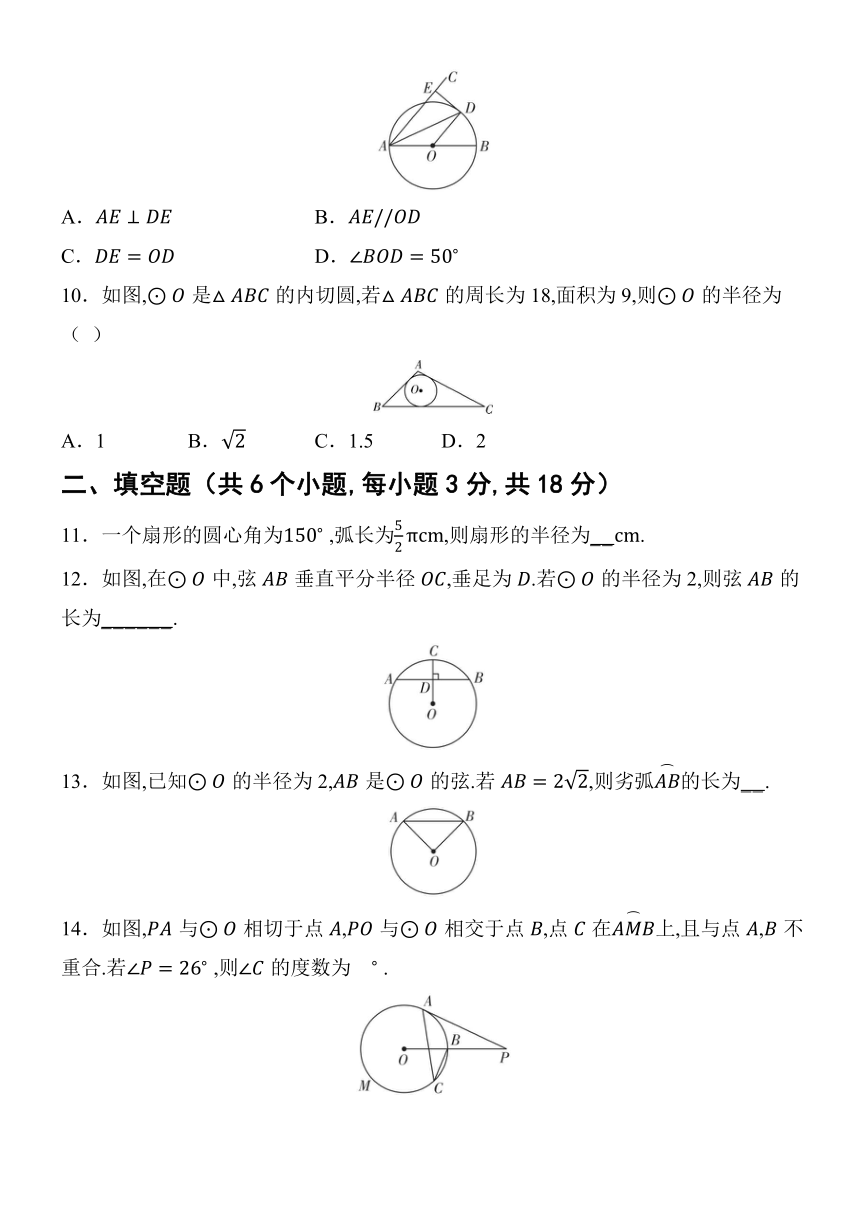
7.中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为,曲线终点为,过点,的两条切线相交于点,列车在从点到点行驶的过程中转角 为 .若圆曲线的半径,则这段圆曲线的长为( )
A. B. C. D.
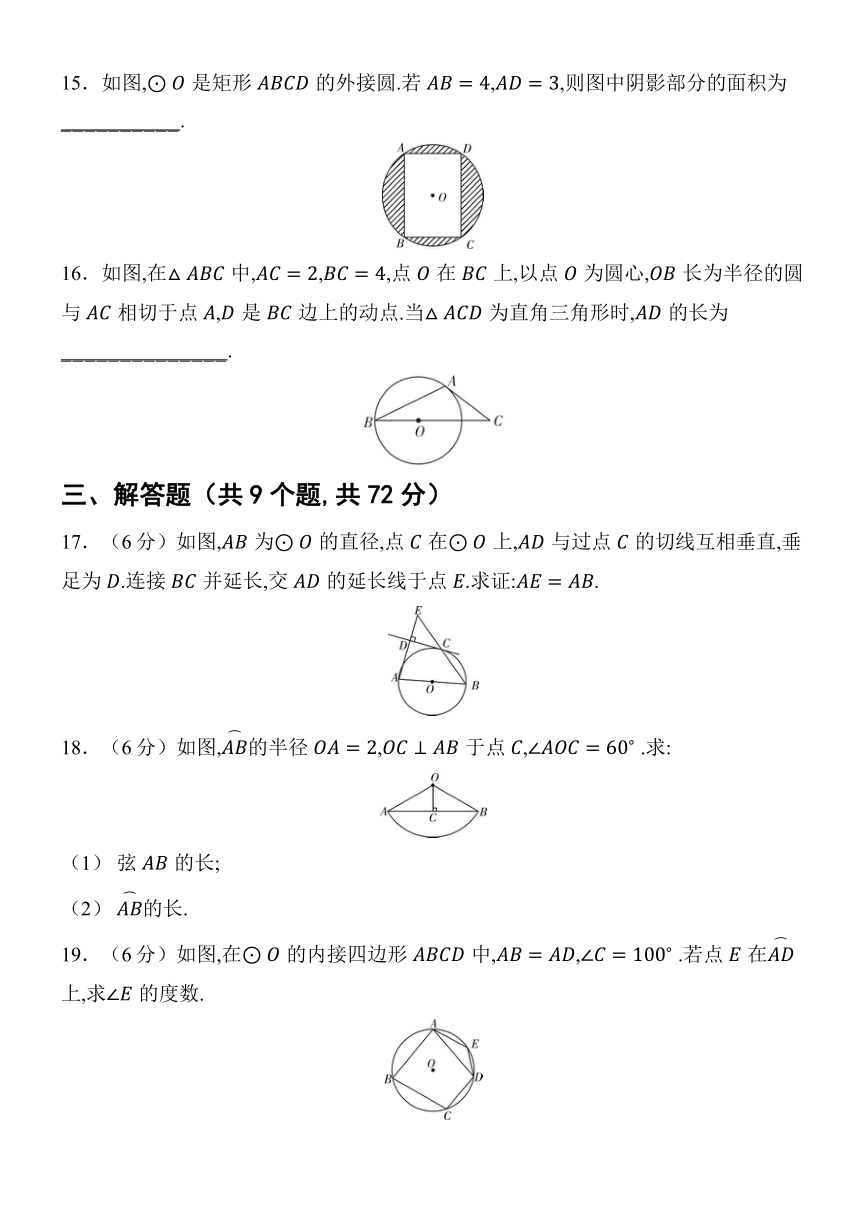
8.如图,在边长为2的正方形中,是以为直径的半圆的切线,则图中阴影部分的面积为( )
A. B. C.1 D.
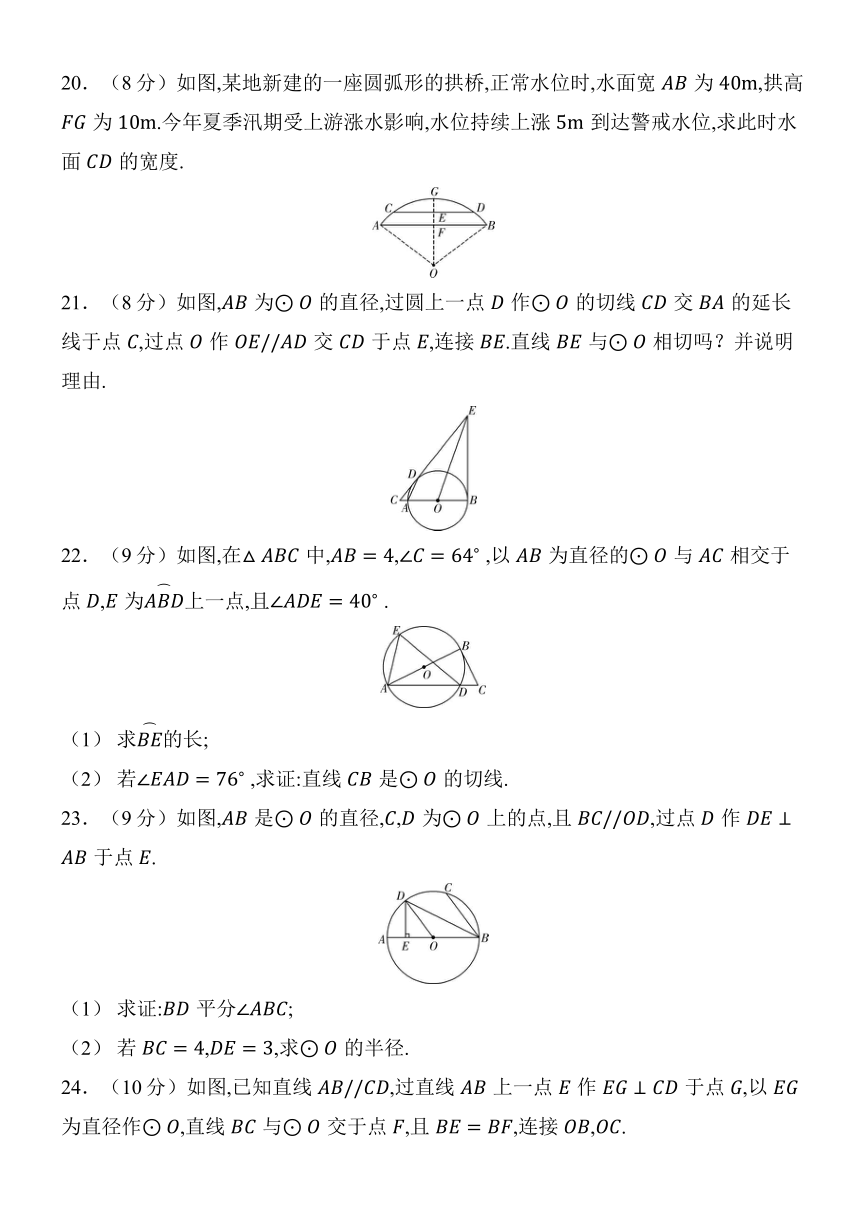
9.如图,是的直径,弦平分,过点的切线交于点, ,则下列结论错误的是( )
A. B.
C. D.
10.如图,是的内切圆,若的周长为18,面积为9,则的半径为( )
A.1 B. C.1.5 D.2
二、填空题(共6个小题,每小题3分,共18分)
11.一个扇形的圆心角为 ,弧长为,则扇形的半径为_ _ .
12.如图,在中,弦垂直平分半径,垂足为.若的半径为2,则弦的长为_ _ _ _ _ _ .
13.如图,已知的半径为2,是的弦.若,则劣弧的长为_ _ .
14.如图,与相切于点,与相交于点,点在上,且与点,不重合.若 ,则的度数为 .
15.如图,是矩形的外接圆.若,,则图中阴影部分的面积为_ _ _ _ _ _ _ _ _ _ .
16.如图,在中,,,点在上,以点为圆心,长为半径的圆与相切于点,是边上的动点.当为直角三角形时,的长为_ _ _ _ _ _ _ _ _ _ _ _ _ _ .
三、解答题(共9个题,共72分)
17.(6分)如图,为的直径,点在上,与过点的切线互相垂直,垂足为.连接并延长,交的延长线于点.求证:.
18.(6分)如图,的半径,于点, .求:
(1) 弦的长;
(2) 的长.
19.(6分)如图,在的内接四边形中,, .若点在上,求的度数.
20.(8分)如图,某地新建的一座圆弧形的拱桥,正常水位时,水面宽为,拱高为.今年夏季汛期受上游涨水影响,水位持续上涨到达警戒水位,求此时水面的宽度.
21.(8分)如图,为的直径,过圆上一点作的切线交的延长线于点,过点作交于点,连接.直线与相切吗?并说明理由.
22.(9分)如图,在中,, ,以为直径的与相交于点,为上一点,且 .
(1) 求的长;
(2) 若 ,求证:直线是的切线.
23.(9分)如图,是的直径,,为上的点,且,过点作于点.
(1) 求证:平分;
(2) 若,,求的半径.
24.(10分)如图,已知直线,过直线上一点作于点,以为直径作,直线与交于点,且,连接,.
(1) 求证:直线是的切线;
(2) 若的半径为3,且,求的值.
25.(10分)如图①,四边形内接于,为直径,过点作,交的延长线于点,连接.
①
(1) 求证:.
(2) 若是的切线, ,连接,如图②.
②
① 请判断四边形的形状,并说明理由;
② 当时,求图中阴影部分的面积.
第二十四章质量评估
一、选择题(共10个小题,每小题3分,共30分)
1.A 2.C 3.C 4.B 5.A 6.C 7.B 8.D 9.C 10.A
二、填空题(共6个小题,每小题3分,共18分)
11.3
12.
13.
14.32
15.
16.或
三、解答题(共9个题,共72分)
17.证明:如答图,连接.
第17题答图
为切线,.
,,,
,,
,.
18.(1) 解:的半径,, ,
,,
,.
(2) , , .
,的长为.
19.解:如答图,连接.
第19题答图
四边形是圆内接四边形,
,
.
,,
.
四边形为圆内接四边形,
,
.
20.解:由题意,知,.
设,则.
在中,根据勾股定理,得,
解得,则.
连接(图略),在中,
,
,
.
即水位到达警戒水位时,水面的宽为.
21.解:直线与相切.理由如下:
如答图,连接.
切于点,,即 .
,.
,,,
.
在和中,
,
,即.
为的半径, 直线与相切.
第21题答图
22.(1) 解:如答图,连接.
,
,
.
,的半径是2,
的长为.
第22题答图
(2) 证明: , ,
.
,
,
直径, 直线是的切线.
23.(1) 证明:,.
,,
,平分.
(2) 解:如答图,过点作于点.
,.
,,
, .
,.
在和中,
,.
在中,.
即的半径为.
第23题答图
24.(1) 证明:如答图,连接.
,,,
.
在和中,
,
,即.
是的半径, 直线是的切线.
第24题答图
(2) 解:如答图,过点作于点.
在和中,
,,
,
,
,即.
在中,
.
25.(1) 证明: 四边形是的内接四边形,
.
为的直径, ,
, .
, ,.
(2) ① 解:四边形是菱形.理由如下:
,
, .
是的切线,.
,, .
由(1)知, ,
,
, 四边形是平行四边形.
, 四边形是菱形.
② 由①,知四边形是菱形,
,.
由①知, .
在中, ,,.
.
[时间:120分钟 分值:120分]
一、选择题(共10个小题,每小题3分,共30分)
1.已知点在外,,那么的半径可能为( )
A. B. C. D.
2.如图,点,,在上,连接,,,.若 ,则的度数为( )
A. B. C. D.
3.如图,是的弦,若的半径,圆心到弦的距离,则弦的长为( )
A.4 B.6 C.8 D.10
4.如图,,是的切线,,为切点,是的直径, ,则的度数为( )
A. B. C. D.
5.如图,是的直径,,是上的两点.若 ,则的度数为( )
A. B. C. D.
6.如图,等边三角形的顶点在上,边,与分别交于点,,是上一点,且与点,不重合,连接,,则的度数为( )
A. B. C. D.
7.中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为,曲线终点为,过点,的两条切线相交于点,列车在从点到点行驶的过程中转角 为 .若圆曲线的半径,则这段圆曲线的长为( )
A. B. C. D.
8.如图,在边长为2的正方形中,是以为直径的半圆的切线,则图中阴影部分的面积为( )
A. B. C.1 D.
9.如图,是的直径,弦平分,过点的切线交于点, ,则下列结论错误的是( )
A. B.
C. D.
10.如图,是的内切圆,若的周长为18,面积为9,则的半径为( )
A.1 B. C.1.5 D.2
二、填空题(共6个小题,每小题3分,共18分)
11.一个扇形的圆心角为 ,弧长为,则扇形的半径为_ _ .
12.如图,在中,弦垂直平分半径,垂足为.若的半径为2,则弦的长为_ _ _ _ _ _ .
13.如图,已知的半径为2,是的弦.若,则劣弧的长为_ _ .
14.如图,与相切于点,与相交于点,点在上,且与点,不重合.若 ,则的度数为 .
15.如图,是矩形的外接圆.若,,则图中阴影部分的面积为_ _ _ _ _ _ _ _ _ _ .
16.如图,在中,,,点在上,以点为圆心,长为半径的圆与相切于点,是边上的动点.当为直角三角形时,的长为_ _ _ _ _ _ _ _ _ _ _ _ _ _ .
三、解答题(共9个题,共72分)
17.(6分)如图,为的直径,点在上,与过点的切线互相垂直,垂足为.连接并延长,交的延长线于点.求证:.
18.(6分)如图,的半径,于点, .求:
(1) 弦的长;
(2) 的长.
19.(6分)如图,在的内接四边形中,, .若点在上,求的度数.
20.(8分)如图,某地新建的一座圆弧形的拱桥,正常水位时,水面宽为,拱高为.今年夏季汛期受上游涨水影响,水位持续上涨到达警戒水位,求此时水面的宽度.
21.(8分)如图,为的直径,过圆上一点作的切线交的延长线于点,过点作交于点,连接.直线与相切吗?并说明理由.
22.(9分)如图,在中,, ,以为直径的与相交于点,为上一点,且 .
(1) 求的长;
(2) 若 ,求证:直线是的切线.
23.(9分)如图,是的直径,,为上的点,且,过点作于点.
(1) 求证:平分;
(2) 若,,求的半径.
24.(10分)如图,已知直线,过直线上一点作于点,以为直径作,直线与交于点,且,连接,.
(1) 求证:直线是的切线;
(2) 若的半径为3,且,求的值.
25.(10分)如图①,四边形内接于,为直径,过点作,交的延长线于点,连接.
①
(1) 求证:.
(2) 若是的切线, ,连接,如图②.
②
① 请判断四边形的形状,并说明理由;
② 当时,求图中阴影部分的面积.
第二十四章质量评估
一、选择题(共10个小题,每小题3分,共30分)
1.A 2.C 3.C 4.B 5.A 6.C 7.B 8.D 9.C 10.A
二、填空题(共6个小题,每小题3分,共18分)
11.3
12.
13.
14.32
15.
16.或
三、解答题(共9个题,共72分)
17.证明:如答图,连接.
第17题答图
为切线,.
,,,
,,
,.
18.(1) 解:的半径,, ,
,,
,.
(2) , , .
,的长为.
19.解:如答图,连接.
第19题答图
四边形是圆内接四边形,
,
.
,,
.
四边形为圆内接四边形,
,
.
20.解:由题意,知,.
设,则.
在中,根据勾股定理,得,
解得,则.
连接(图略),在中,
,
,
.
即水位到达警戒水位时,水面的宽为.
21.解:直线与相切.理由如下:
如答图,连接.
切于点,,即 .
,.
,,,
.
在和中,
,
,即.
为的半径, 直线与相切.
第21题答图
22.(1) 解:如答图,连接.
,
,
.
,的半径是2,
的长为.
第22题答图
(2) 证明: , ,
.
,
,
直径, 直线是的切线.
23.(1) 证明:,.
,,
,平分.
(2) 解:如答图,过点作于点.
,.
,,
, .
,.
在和中,
,.
在中,.
即的半径为.
第23题答图
24.(1) 证明:如答图,连接.
,,,
.
在和中,
,
,即.
是的半径, 直线是的切线.
第24题答图
(2) 解:如答图,过点作于点.
在和中,
,,
,
,
,即.
在中,
.
25.(1) 证明: 四边形是的内接四边形,
.
为的直径, ,
, .
, ,.
(2) ① 解:四边形是菱形.理由如下:
,
, .
是的切线,.
,, .
由(1)知, ,
,
, 四边形是平行四边形.
, 四边形是菱形.
② 由①,知四边形是菱形,
,.
由①知, .
在中, ,,.
.
同课章节目录
