21.2 解一元二次方程 21.3 实际问题与一元二次方程 提能集训(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 21.2 解一元二次方程 21.3 实际问题与一元二次方程 提能集训(含答案) 2025-2026学年数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 81.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 00:00:00 | ||
图片预览


文档简介
21.2 解一元二次方程 21.3 实际问题与一元二次方程 提能集训
[测试时间:45分钟 测试范围:21.2~21.3分值:100分]
一、选择题(每小题5分,共30分)
1.[2023娄底模拟]是下列哪个一元二次方程的根( )
A. B.
C. D.
2.[2024邵阳模拟]若,是一元二次方程的两个根,则的值是( )
A.3 B. C.4 D.
3.关于的一元二次方程的一个根为1,则另一个根为( )
A. B.2 C.4 D.1
4.[2023张家界模拟]某公司前年缴税40万元,今年缴税48.4万元,则该公司缴税的年均增长率为( )
A. B. C. D.
5.[2024常德模拟]若实数,满足,,且,则的值为( )
A.18 B.12 C.9 D.6
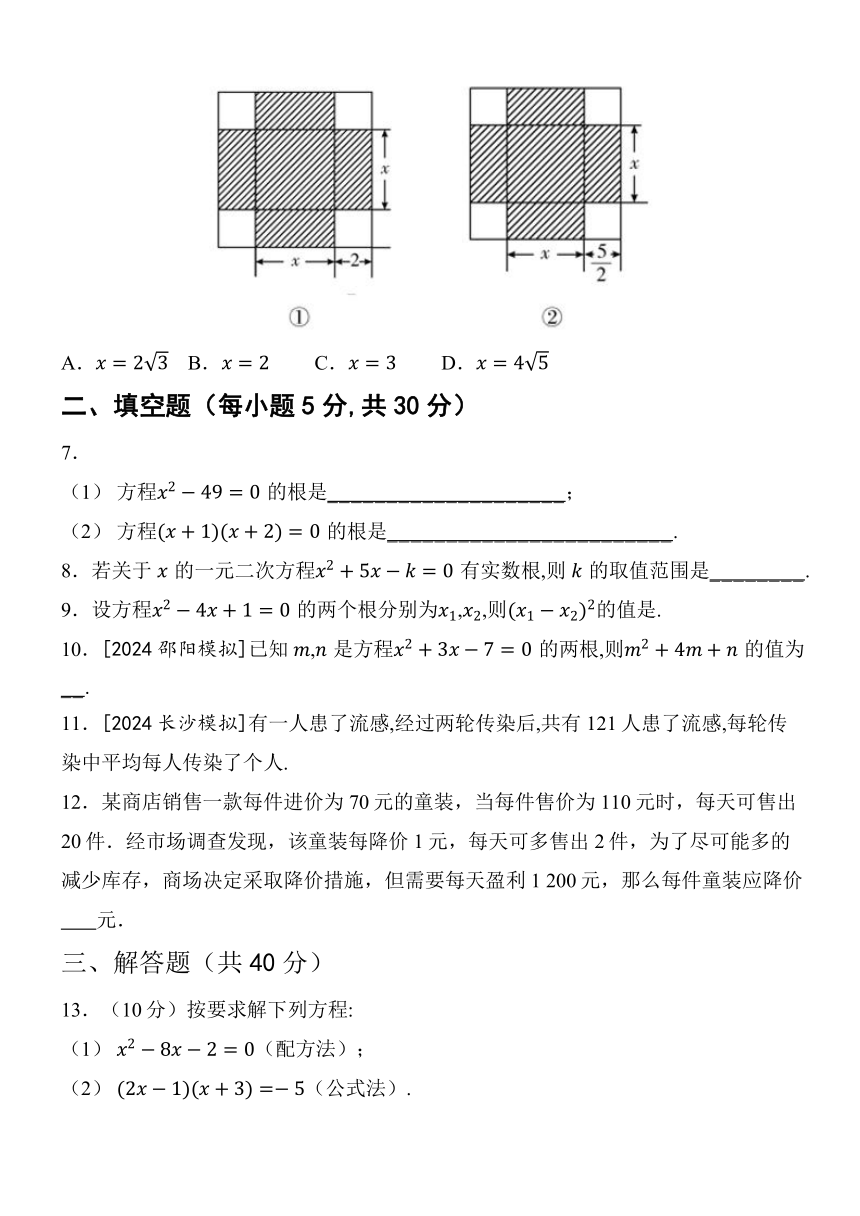
6.在《代数学》中记载了求方程正数解的几何方法:如图①,先构造1个面积为的正方形,再以正方形的边为一边向外构造4个面积为的矩形,得到大正方形的面积为,则该方程的正数解为.小明尝试用此方法解关于的方程时,构造出如图②的正方形.已知图②中阴影部分的面积和为39,则该方程的正数解为( )
A. B. C. D.
二、填空题(每小题5分,共30分)
7.
(1) 方程的根是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ;
(2) 方程的根是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
8.若关于的一元二次方程有实数根,则的取值范围是_ _ _ _ _ _ _ _ .
9.设方程的两个根分别为,,则的值是.
10.[2024邵阳模拟]已知,是方程的两根,则的值为_ _ .
11.[2024长沙模拟]有一人患了流感,经过两轮传染后,共有121人患了流感,每轮传染中平均每人传染了个人.
12.某商店销售一款每件进价为70元的童装,当每件售价为110元时,每天可售出20件.经市场调查发现,该童装每降价1元,每天可多售出2件,为了尽可能多的减少库存,商场决定采取降价措施,但需要每天盈利1 200元,那么每件童装应降价
元.
三、解答题(共40分)
13.(10分)按要求解下列方程:
(1) (配方法);
(2) (公式法).
14.[2023郴州模拟](10分)已知关于的一元二次方程有两个实数根.
(1) 求的取值范围;
(2) 若,求的值.
15.(10分)在丝绸博览会期间,某公司展销如图所示的长方形工艺品,该工艺品长,宽,中间镶有宽度相同的三条丝绸条带.
(1) 若丝绸条带的面积为,求丝绸条带的宽度.
(2) 已知该工艺品的成本是40元/件,若以单价为100元/件销售,则每天可售出200件,另外每天除工艺品的成本外所需支付的各种费用是2 000元.根据销售经验,如果将销售单价每降低1元,每天可多售出20件.请问该公司每天把销售单价定为每件多少元时,当日所获利润为22 500元
16.[2024岳阳模拟](10分)如果关于的一元二次方程有两个实数根,且其中一个根是另一个根的倍(为正整数),则称这样的方程为“倍根方程”.例如:方程的两个根分别是2和4,则这个方程就是“二倍根方程”.
(1) 根据上述定义,是“倍根方程”;
(2) 若关于的一元二次方程是“三倍根方程”,求的值;
(3) 若关于的一元二次方程是“倍根方程”,请探究与之间的数量关系(用含的代数式表示);
(4) 由(3)中发现的,之间的数量关系,不难得到的最小值是_ _ .(参考公式:,,均为正数)
一、选择题(每小题5分,共30分)
1.D 2.D 3.C 4.B 5.A 6.C
二、填空题(每小题5分,共30分)
7.(1) ,
(2) ,
8.
9.12
10.4
11.10
12.20
三、解答题(共40分)
13.(1) 解:原方程可化为,
,
,
,
,.
(2) 整理,得,
,
,
,.
14.(1) 解: 关于的一元二次方程有两个实数根,
,即,
解得.
(2) 关于的一元二次方程的两个实数根为,,
,.
,
,
,
整理,得,
解得或,
,的值为.
15.(1) 解:设丝绸条带的宽度为.
由题意,得
,
整理,得,
解得,(不合题意,舍去).
答:丝绸条带的宽度为.
(2) 设每件工艺品降价元出售.
由题意,得
.
解得.
售价为(元/件).
答:当销售单价定为75元/件时,当日所获利润为22 500元.
16.(1) 四
(2) 解:由题意,可设与是方程的两个根,
解得
的值为.
(3) 关于的一元二次方程是“倍根方程”,
设与是方程的两个根,
消去,得.
(4) 1
[测试时间:45分钟 测试范围:21.2~21.3分值:100分]
一、选择题(每小题5分,共30分)
1.[2023娄底模拟]是下列哪个一元二次方程的根( )
A. B.
C. D.
2.[2024邵阳模拟]若,是一元二次方程的两个根,则的值是( )
A.3 B. C.4 D.
3.关于的一元二次方程的一个根为1,则另一个根为( )
A. B.2 C.4 D.1
4.[2023张家界模拟]某公司前年缴税40万元,今年缴税48.4万元,则该公司缴税的年均增长率为( )
A. B. C. D.
5.[2024常德模拟]若实数,满足,,且,则的值为( )
A.18 B.12 C.9 D.6
6.在《代数学》中记载了求方程正数解的几何方法:如图①,先构造1个面积为的正方形,再以正方形的边为一边向外构造4个面积为的矩形,得到大正方形的面积为,则该方程的正数解为.小明尝试用此方法解关于的方程时,构造出如图②的正方形.已知图②中阴影部分的面积和为39,则该方程的正数解为( )
A. B. C. D.
二、填空题(每小题5分,共30分)
7.
(1) 方程的根是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ;
(2) 方程的根是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
8.若关于的一元二次方程有实数根,则的取值范围是_ _ _ _ _ _ _ _ .
9.设方程的两个根分别为,,则的值是.
10.[2024邵阳模拟]已知,是方程的两根,则的值为_ _ .
11.[2024长沙模拟]有一人患了流感,经过两轮传染后,共有121人患了流感,每轮传染中平均每人传染了个人.
12.某商店销售一款每件进价为70元的童装,当每件售价为110元时,每天可售出20件.经市场调查发现,该童装每降价1元,每天可多售出2件,为了尽可能多的减少库存,商场决定采取降价措施,但需要每天盈利1 200元,那么每件童装应降价
元.
三、解答题(共40分)
13.(10分)按要求解下列方程:
(1) (配方法);
(2) (公式法).
14.[2023郴州模拟](10分)已知关于的一元二次方程有两个实数根.
(1) 求的取值范围;
(2) 若,求的值.
15.(10分)在丝绸博览会期间,某公司展销如图所示的长方形工艺品,该工艺品长,宽,中间镶有宽度相同的三条丝绸条带.
(1) 若丝绸条带的面积为,求丝绸条带的宽度.
(2) 已知该工艺品的成本是40元/件,若以单价为100元/件销售,则每天可售出200件,另外每天除工艺品的成本外所需支付的各种费用是2 000元.根据销售经验,如果将销售单价每降低1元,每天可多售出20件.请问该公司每天把销售单价定为每件多少元时,当日所获利润为22 500元
16.[2024岳阳模拟](10分)如果关于的一元二次方程有两个实数根,且其中一个根是另一个根的倍(为正整数),则称这样的方程为“倍根方程”.例如:方程的两个根分别是2和4,则这个方程就是“二倍根方程”.
(1) 根据上述定义,是“倍根方程”;
(2) 若关于的一元二次方程是“三倍根方程”,求的值;
(3) 若关于的一元二次方程是“倍根方程”,请探究与之间的数量关系(用含的代数式表示);
(4) 由(3)中发现的,之间的数量关系,不难得到的最小值是_ _ .(参考公式:,,均为正数)
一、选择题(每小题5分,共30分)
1.D 2.D 3.C 4.B 5.A 6.C
二、填空题(每小题5分,共30分)
7.(1) ,
(2) ,
8.
9.12
10.4
11.10
12.20
三、解答题(共40分)
13.(1) 解:原方程可化为,
,
,
,
,.
(2) 整理,得,
,
,
,.
14.(1) 解: 关于的一元二次方程有两个实数根,
,即,
解得.
(2) 关于的一元二次方程的两个实数根为,,
,.
,
,
,
整理,得,
解得或,
,的值为.
15.(1) 解:设丝绸条带的宽度为.
由题意,得
,
整理,得,
解得,(不合题意,舍去).
答:丝绸条带的宽度为.
(2) 设每件工艺品降价元出售.
由题意,得
.
解得.
售价为(元/件).
答:当销售单价定为75元/件时,当日所获利润为22 500元.
16.(1) 四
(2) 解:由题意,可设与是方程的两个根,
解得
的值为.
(3) 关于的一元二次方程是“倍根方程”,
设与是方程的两个根,
消去,得.
(4) 1
同课章节目录
