专题3 旋转 题型归类练习(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 专题3 旋转 题型归类练习(含答案) 2025-2026学年数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 431.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 00:00:00 | ||
图片预览


文档简介
专题3 旋转
题型归类 举一反三
题型一 轴对称图形与中心对称图形
例1 下列四幅图案中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
变式跟进
1.下列城市地铁的标志图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
题型二 旋转的概念及计算
例2 如图,将绕点顺时针旋转后,得到,且点在边上.若 ,则的度数为( )
A. B. C. D.
变式跟进
2.[2024秋和平区期末]如图,将Rt△ABC绕点A顺时针旋转a得到Rt△AB'C',点C恰好落在AB上,连接BB'.若∠BB'C'=30°,则a= °.
题型三 坐标系中的旋转作图
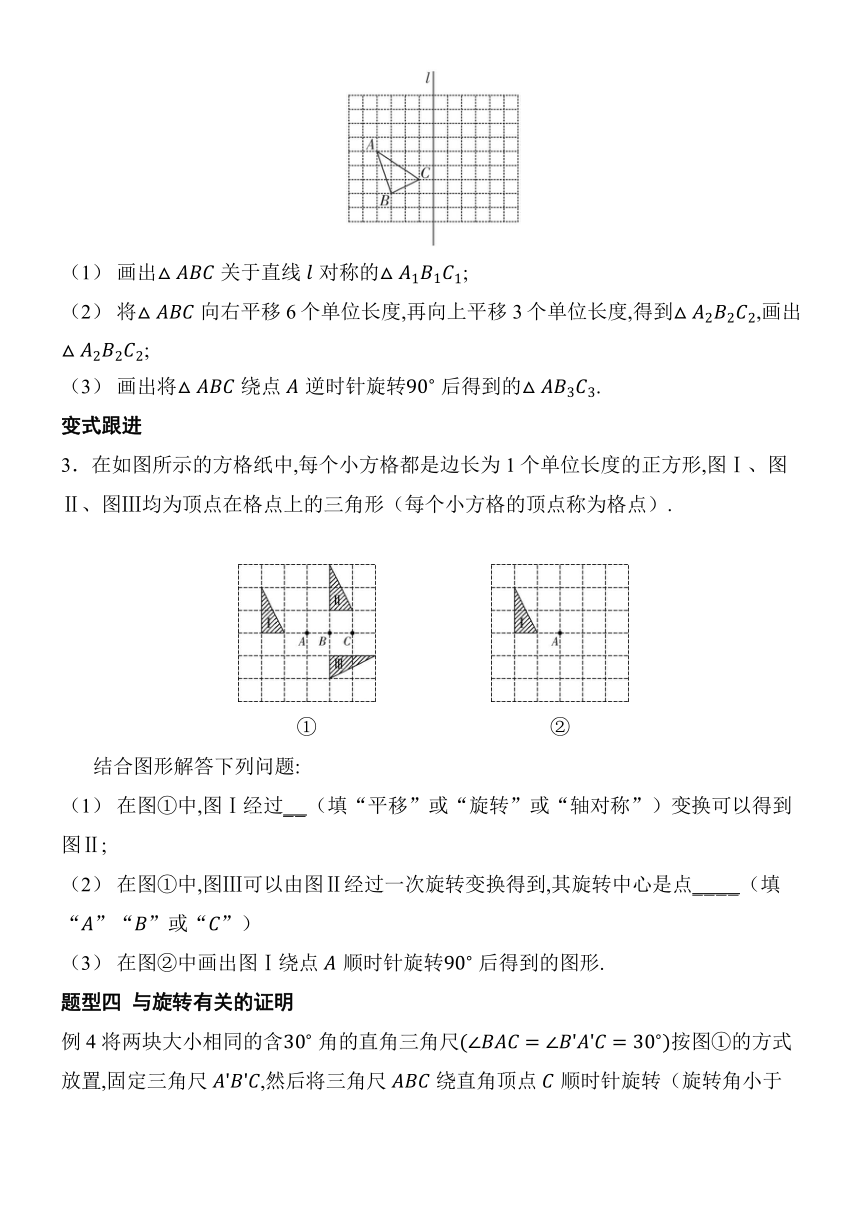
例3 [2023怀化模拟]如图,已知的顶点都在格点上,直线与网线重合(每个小正方形的边长均为1个单位长度).
(1) 画出关于直线对称的;
(2) 将向右平移6个单位长度,再向上平移3个单位长度,得到,画出;
(3) 画出将绕点逆时针旋转 后得到的.
变式跟进
3.在如图所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,图Ⅰ、图Ⅱ、图Ⅲ均为顶点在格点上的三角形(每个小方格的顶点称为格点).
① ②
结合图形解答下列问题:
(1) 在图①中,图Ⅰ经过_ _ (填“平移”或“旋转”或“轴对称”)变换可以得到图Ⅱ;
(2) 在图①中,图Ⅲ可以由图Ⅱ经过一次旋转变换得到,其旋转中心是点_ _ _ _ (填“”“”或“”)
(3) 在图②中画出图Ⅰ绕点顺时针旋转 后得到的图形.
题型四 与旋转有关的证明
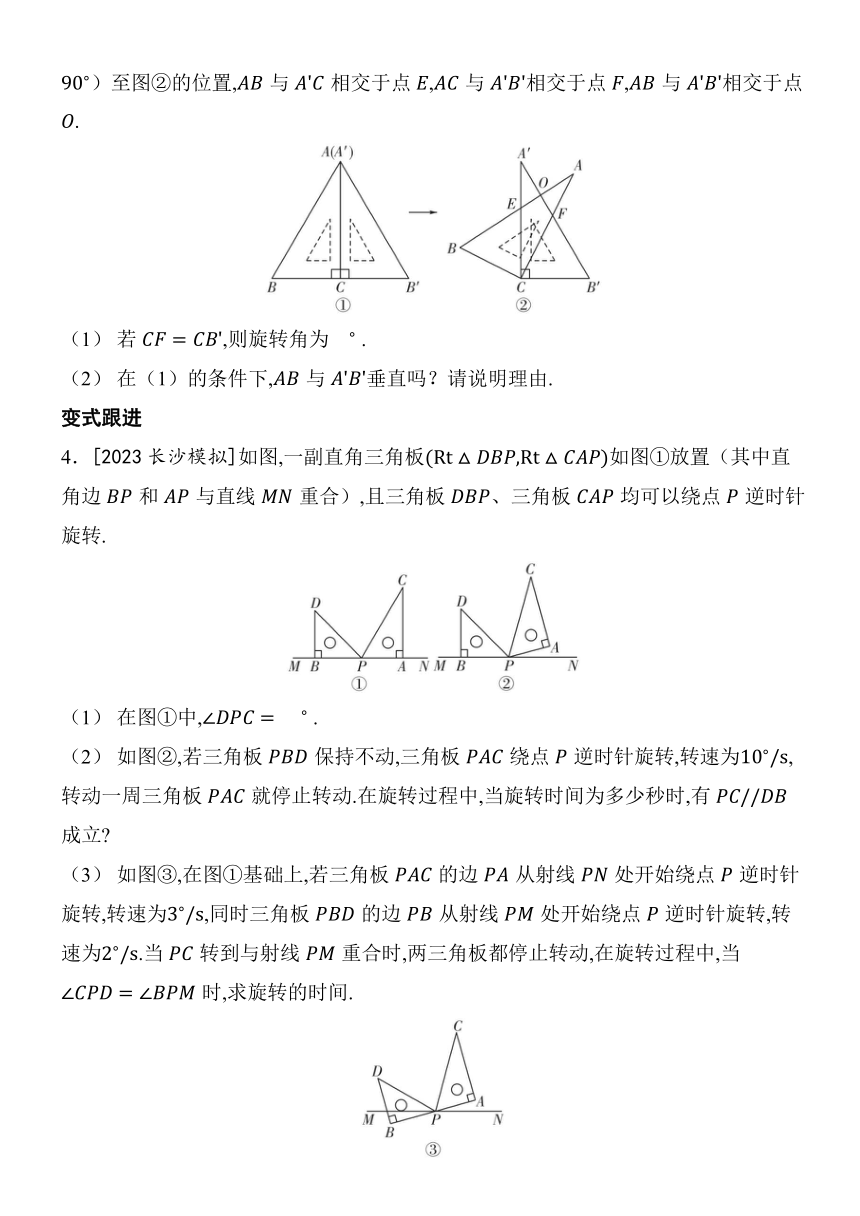
例4 将两块大小相同的含 角的直角三角尺按图①的方式放置,固定三角尺,然后将三角尺绕直角顶点顺时针旋转(旋转角小于)至图②的位置,与相交于点,与相交于点,与相交于点.
(1) 若,则旋转角为 .
(2) 在(1)的条件下,与垂直吗?请说明理由.
变式跟进
4.[2023长沙模拟]如图,一副直角三角板如图①放置(其中直角边和与直线重合),且三角板、三角板均可以绕点逆时针旋转.
(1) 在图①中, .
(2) 如图②,若三角板保持不动,三角板绕点逆时针旋转,转速为,转动一周三角板就停止转动.在旋转过程中,当旋转时间为多少秒时,有成立
(3) 如图③,在图①基础上,若三角板的边从射线处开始绕点逆时针旋转,转速为,同时三角板的边从射线处开始绕点逆时针旋转,转速为.当转到与射线重合时,两三角板都停止转动,在旋转过程中,当时,求旋转的时间.
过关训练 现复活用
A组·基础达标 逐点击破
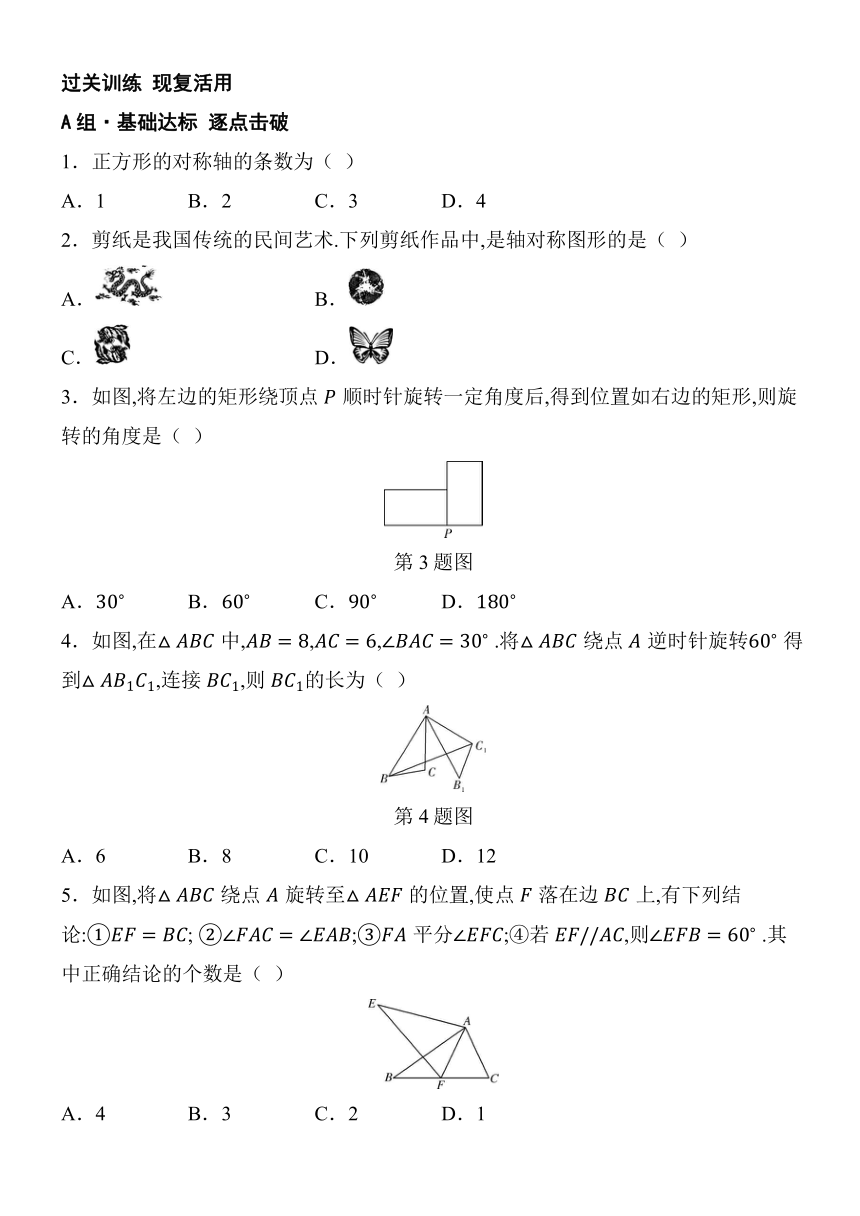
1.正方形的对称轴的条数为( )
A.1 B.2 C.3 D.4
2.剪纸是我国传统的民间艺术.下列剪纸作品中,是轴对称图形的是( )
A. B.
C. D.
3.如图,将左边的矩形绕顶点顺时针旋转一定角度后,得到位置如右边的矩形,则旋转的角度是( )
第3题图
A. B. C. D.
4.如图,在中,,, .将绕点逆时针旋转 得到,连接,则的长为( )
第4题图
A.6 B.8 C.10 D.12
5.如图,将绕点旋转至的位置,使点落在边上,有下列结论:; ;平分;④若,则 .其中正确结论的个数是( )
A.4 B.3 C.2 D.1
6.[2023长沙模拟]已知点与点关于原点成中心对称,则的值为_ _ _ _ _ _ _ _ .
7.[2024宁乡模拟]如图,在平面直角坐标系中,的顶点坐标分别为,,.
(1) 画出关于点成中心对称的;
(2) 写出坐标:_ _ _ _ _ _ _ _ _ _ ,_ _ _ _ _ _ _ _ .
8.[2024娄底模拟]如图,在中,点在边上,,将线段绕点旋转到的位置,使得,连接,与交于点.
(1) 求证:;
(2) 若 , ,求的度数.
B组·能力提升 强化突破
9.如图,将矩形绕点旋转得到矩形,点在上,延长交于点.
(1) 求证:;
(2) 连接,若 ,求的度数.
10.[2024衡阳模拟]如图,已知四边形是正方形,点在上,将顺时针旋转后与完全重合,再将线段向右平移后与完全重合.
(1) 旋转中心是点_ _ _ _ ,旋转角度是 ;
(2) 试猜想线段和的数量关系和位置关系,并说明理由.
11.[2023娄底模拟]定义:如图①,在中,把绕点顺时针旋转得到,把绕点逆时针旋转 得到,连接.当 时,我们称是的“旋补三角形”,边上的中线称为的“旋补中线”,点称为“旋补中心”.
【特例感知】
(1) 在图②,图③中,是的“旋补三角形”,是的“旋补中线”.
① 如图②,当为等边三角形时,与的数量关系_ _ _ _ _ _ ;
② 如图③,当 ,时,的长为_ _ .
【猜想论证】
(2) 在图①中,当为任意三角形时,猜想与的数量关系,并给予证明.
专题3 旋转
题型归类 举一反三
题型一 轴对称图形与中心对称图形
【点悟】 判断一个图形是不是轴对称图形,就是看它能否沿某一条直线对折,使图形被直线分成的两部分完全重合;判断一个图形是不是中心对称图形,就是看图形能否绕某一点旋转 后与本身重合.
例1 D
变式跟进
1.C
题型二 旋转的概念及计算
【点悟】 旋转前后的图形有如下特征:(1)对应点到旋转中心的距离相等;(2)对应点与旋转中心所连线段的夹角等于旋转角;(3)旋转前后的图形全等.
例2 C
变式跟进
2.
题型三 坐标系中的旋转作图
例3 (1) 解:如答图,即为所求作.
例3答图
(2) 如答图,即为所求作.
例3答图
(3) 如答图,即为所求作.
例3答图
变式跟进
3.(1) 平移
(2)
(3) 解:旋转后的图形如答图所示.
变式跟进3答图
题型四 与旋转有关的证明
例4 (1) 30
(2) 解:.理由如下:
,,
, .
又 ,
,
.
变式跟进
4.(1) 75
(2) 解:①如答图①,此时,成立,
变式跟进4答图①
, ,
.
, ,
.
转速为,
旋转时间为;
如答图②,,
变式跟进4答图②
, ,
,
, ,
,
三角板绕点逆时针旋转到达该位置时的旋转角为 .
转速为, 旋转时间为,
综上所述,当旋转时间为或时,成立.
(3) 设旋转的时间为,由题知 , ,
,
,
当,
即 ,解得,
此时未与射线重合.
当时,旋转的时间是.
过关训练 现复活用
A组·基础达标 逐点击破
1.D 2.D 3.C 4.C 5.A
6.
7.(1) 解:如答图,即为所求作.
第7题答图
(2) ;
8.(1) 证明:,
.
将线段绕点旋转到的位置,
.
在和中,
,
.
(2) 解:, ,
,
.
,
,
.
B组·能力提升 强化突破
9.(1) 证明: 四边形是矩形,
, .
由旋转的性质,得, ,
,.
在矩形中,,
.
在和中,
.
(2) 解:四边形是矩形,
,
.
,
,
.
,
.
10.(1) ; 90
(2) 解:且.理由如下:
由旋转的性质,可得, .
由平移的性质,可得,,
.
,
,
.
11.(1) ①
[解析]是等边三角形,
, .
是的“旋补三角形”,
,,,
,
,
,
.
② 4
[解析]是的“旋补三角形”,
,,.
在和中,
,
.
,是的“旋补中线”,
.
(2) 解:猜想:.
证明:如答图,延长至点,使得,连接,.
第11题答图
是的中线,
.
,
四边形是平行四边形,
, .
,
,
.
在和中,
,
,
.
题型归类 举一反三
题型一 轴对称图形与中心对称图形
例1 下列四幅图案中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
变式跟进
1.下列城市地铁的标志图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
题型二 旋转的概念及计算
例2 如图,将绕点顺时针旋转后,得到,且点在边上.若 ,则的度数为( )
A. B. C. D.
变式跟进
2.[2024秋和平区期末]如图,将Rt△ABC绕点A顺时针旋转a得到Rt△AB'C',点C恰好落在AB上,连接BB'.若∠BB'C'=30°,则a= °.
题型三 坐标系中的旋转作图
例3 [2023怀化模拟]如图,已知的顶点都在格点上,直线与网线重合(每个小正方形的边长均为1个单位长度).
(1) 画出关于直线对称的;
(2) 将向右平移6个单位长度,再向上平移3个单位长度,得到,画出;
(3) 画出将绕点逆时针旋转 后得到的.
变式跟进
3.在如图所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,图Ⅰ、图Ⅱ、图Ⅲ均为顶点在格点上的三角形(每个小方格的顶点称为格点).
① ②
结合图形解答下列问题:
(1) 在图①中,图Ⅰ经过_ _ (填“平移”或“旋转”或“轴对称”)变换可以得到图Ⅱ;
(2) 在图①中,图Ⅲ可以由图Ⅱ经过一次旋转变换得到,其旋转中心是点_ _ _ _ (填“”“”或“”)
(3) 在图②中画出图Ⅰ绕点顺时针旋转 后得到的图形.
题型四 与旋转有关的证明
例4 将两块大小相同的含 角的直角三角尺按图①的方式放置,固定三角尺,然后将三角尺绕直角顶点顺时针旋转(旋转角小于)至图②的位置,与相交于点,与相交于点,与相交于点.
(1) 若,则旋转角为 .
(2) 在(1)的条件下,与垂直吗?请说明理由.
变式跟进
4.[2023长沙模拟]如图,一副直角三角板如图①放置(其中直角边和与直线重合),且三角板、三角板均可以绕点逆时针旋转.
(1) 在图①中, .
(2) 如图②,若三角板保持不动,三角板绕点逆时针旋转,转速为,转动一周三角板就停止转动.在旋转过程中,当旋转时间为多少秒时,有成立
(3) 如图③,在图①基础上,若三角板的边从射线处开始绕点逆时针旋转,转速为,同时三角板的边从射线处开始绕点逆时针旋转,转速为.当转到与射线重合时,两三角板都停止转动,在旋转过程中,当时,求旋转的时间.
过关训练 现复活用
A组·基础达标 逐点击破
1.正方形的对称轴的条数为( )
A.1 B.2 C.3 D.4
2.剪纸是我国传统的民间艺术.下列剪纸作品中,是轴对称图形的是( )
A. B.
C. D.
3.如图,将左边的矩形绕顶点顺时针旋转一定角度后,得到位置如右边的矩形,则旋转的角度是( )
第3题图
A. B. C. D.
4.如图,在中,,, .将绕点逆时针旋转 得到,连接,则的长为( )
第4题图
A.6 B.8 C.10 D.12
5.如图,将绕点旋转至的位置,使点落在边上,有下列结论:; ;平分;④若,则 .其中正确结论的个数是( )
A.4 B.3 C.2 D.1
6.[2023长沙模拟]已知点与点关于原点成中心对称,则的值为_ _ _ _ _ _ _ _ .
7.[2024宁乡模拟]如图,在平面直角坐标系中,的顶点坐标分别为,,.
(1) 画出关于点成中心对称的;
(2) 写出坐标:_ _ _ _ _ _ _ _ _ _ ,_ _ _ _ _ _ _ _ .
8.[2024娄底模拟]如图,在中,点在边上,,将线段绕点旋转到的位置,使得,连接,与交于点.
(1) 求证:;
(2) 若 , ,求的度数.
B组·能力提升 强化突破
9.如图,将矩形绕点旋转得到矩形,点在上,延长交于点.
(1) 求证:;
(2) 连接,若 ,求的度数.
10.[2024衡阳模拟]如图,已知四边形是正方形,点在上,将顺时针旋转后与完全重合,再将线段向右平移后与完全重合.
(1) 旋转中心是点_ _ _ _ ,旋转角度是 ;
(2) 试猜想线段和的数量关系和位置关系,并说明理由.
11.[2023娄底模拟]定义:如图①,在中,把绕点顺时针旋转得到,把绕点逆时针旋转 得到,连接.当 时,我们称是的“旋补三角形”,边上的中线称为的“旋补中线”,点称为“旋补中心”.
【特例感知】
(1) 在图②,图③中,是的“旋补三角形”,是的“旋补中线”.
① 如图②,当为等边三角形时,与的数量关系_ _ _ _ _ _ ;
② 如图③,当 ,时,的长为_ _ .
【猜想论证】
(2) 在图①中,当为任意三角形时,猜想与的数量关系,并给予证明.
专题3 旋转
题型归类 举一反三
题型一 轴对称图形与中心对称图形
【点悟】 判断一个图形是不是轴对称图形,就是看它能否沿某一条直线对折,使图形被直线分成的两部分完全重合;判断一个图形是不是中心对称图形,就是看图形能否绕某一点旋转 后与本身重合.
例1 D
变式跟进
1.C
题型二 旋转的概念及计算
【点悟】 旋转前后的图形有如下特征:(1)对应点到旋转中心的距离相等;(2)对应点与旋转中心所连线段的夹角等于旋转角;(3)旋转前后的图形全等.
例2 C
变式跟进
2.
题型三 坐标系中的旋转作图
例3 (1) 解:如答图,即为所求作.
例3答图
(2) 如答图,即为所求作.
例3答图
(3) 如答图,即为所求作.
例3答图
变式跟进
3.(1) 平移
(2)
(3) 解:旋转后的图形如答图所示.
变式跟进3答图
题型四 与旋转有关的证明
例4 (1) 30
(2) 解:.理由如下:
,,
, .
又 ,
,
.
变式跟进
4.(1) 75
(2) 解:①如答图①,此时,成立,
变式跟进4答图①
, ,
.
, ,
.
转速为,
旋转时间为;
如答图②,,
变式跟进4答图②
, ,
,
, ,
,
三角板绕点逆时针旋转到达该位置时的旋转角为 .
转速为, 旋转时间为,
综上所述,当旋转时间为或时,成立.
(3) 设旋转的时间为,由题知 , ,
,
,
当,
即 ,解得,
此时未与射线重合.
当时,旋转的时间是.
过关训练 现复活用
A组·基础达标 逐点击破
1.D 2.D 3.C 4.C 5.A
6.
7.(1) 解:如答图,即为所求作.
第7题答图
(2) ;
8.(1) 证明:,
.
将线段绕点旋转到的位置,
.
在和中,
,
.
(2) 解:, ,
,
.
,
,
.
B组·能力提升 强化突破
9.(1) 证明: 四边形是矩形,
, .
由旋转的性质,得, ,
,.
在矩形中,,
.
在和中,
.
(2) 解:四边形是矩形,
,
.
,
,
.
,
.
10.(1) ; 90
(2) 解:且.理由如下:
由旋转的性质,可得, .
由平移的性质,可得,,
.
,
,
.
11.(1) ①
[解析]是等边三角形,
, .
是的“旋补三角形”,
,,,
,
,
,
.
② 4
[解析]是的“旋补三角形”,
,,.
在和中,
,
.
,是的“旋补中线”,
.
(2) 解:猜想:.
证明:如答图,延长至点,使得,连接,.
第11题答图
是的中线,
.
,
四边形是平行四边形,
, .
,
,
.
在和中,
,
,
.
同课章节目录
