专题4 圆 题型归类练习(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 专题4 圆 题型归类练习(含答案) 2025-2026学年数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 270.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 14:46:23 | ||
图片预览



文档简介
专题4 圆
题型归类 举一反三
题型一 垂径定理及其推论
例1 如图,的直径,弦,,垂足为,则的长为( )
A.5 B.6 C.7 D.8
变式跟进
1.如图,为的弦,为的中点,,,则的半径为( )
A.4 B.5 C.6 D.7
题型二 圆周角定理的综合
例2 如图,为的外接圆的直径,若 ,则_ _ _ _ _ _ .
变式跟进
2.[2023湘西模拟]如图,内接于, ,的平分线交于点.若,,则的长为_ _ .
题型三 点和圆、直线和圆的位置关系
例3 已知的半径为3,点在内,点到圆心的距离为,则的取值范围是( )
A. B. C. D.无法确定
变式跟进
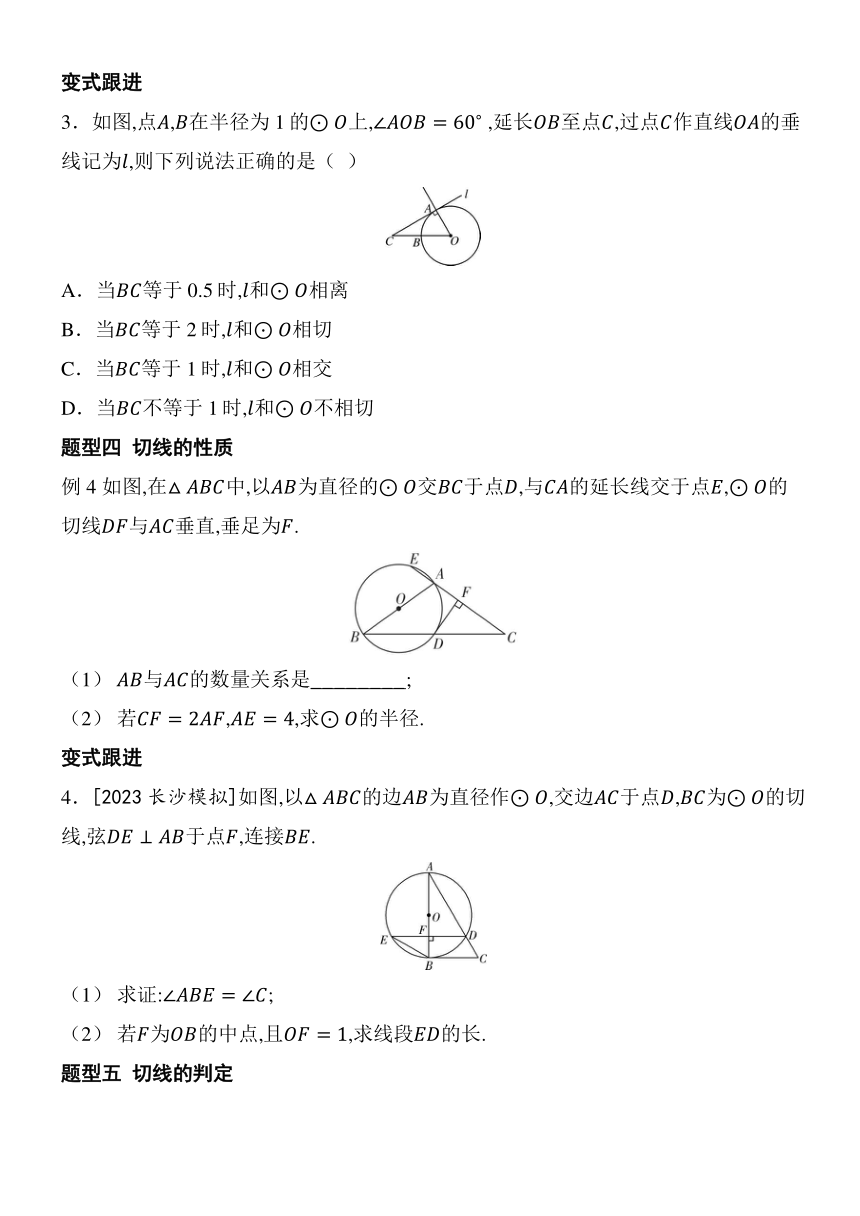
3.如图,点,在半径为1的上, ,延长至点,过点作直线的垂线记为,则下列说法正确的是( )
A.当等于0.5时,和相离
B.当等于2时,和相切
C.当等于1时,和相交
D.当不等于1时,和不相切
题型四 切线的性质
例4 如图,在中,以为直径的交于点,与的延长线交于点,的切线与垂直,垂足为.
(1) 与的数量关系是_ _ _ _ _ _ _ _ ;
(2) 若,,求的半径.
变式跟进
4.[2023长沙模拟]如图,以的边为直径作,交边于点,为的切线,弦于点,连接.
(1) 求证:;
(2) 若为的中点,且,求线段的长.
题型五 切线的判定
例5 [2023长沙模拟]如图,为的直径,为上一点,的平分线交于点,于点.
(1) 试判断直线和的位置关系,并说明理由;
(2) 过点作于点,若 ,,求图中阴影部分的面积.
变式跟进
5.[2023长沙模拟]如图,是的弦,是外一点,,交于点,交于点,且.
(1) 判断直线和的位置关系,并说明理由;
(2) 若 ,,求图中阴影部分的面积.
题型六 切线长定理及三角形的内切圆
例6 《九章算术》是我国古代内容极为丰富的数学著作.书中有下列问题:“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)的直径是多少?( )
A.3步 B.5步 C.6步 D.8步
变式跟进
6.如图,在中, , ,是的内心,延长交的外接圆于点,则的度数是( )
A. B. C. D.
题型七 弧长的计算
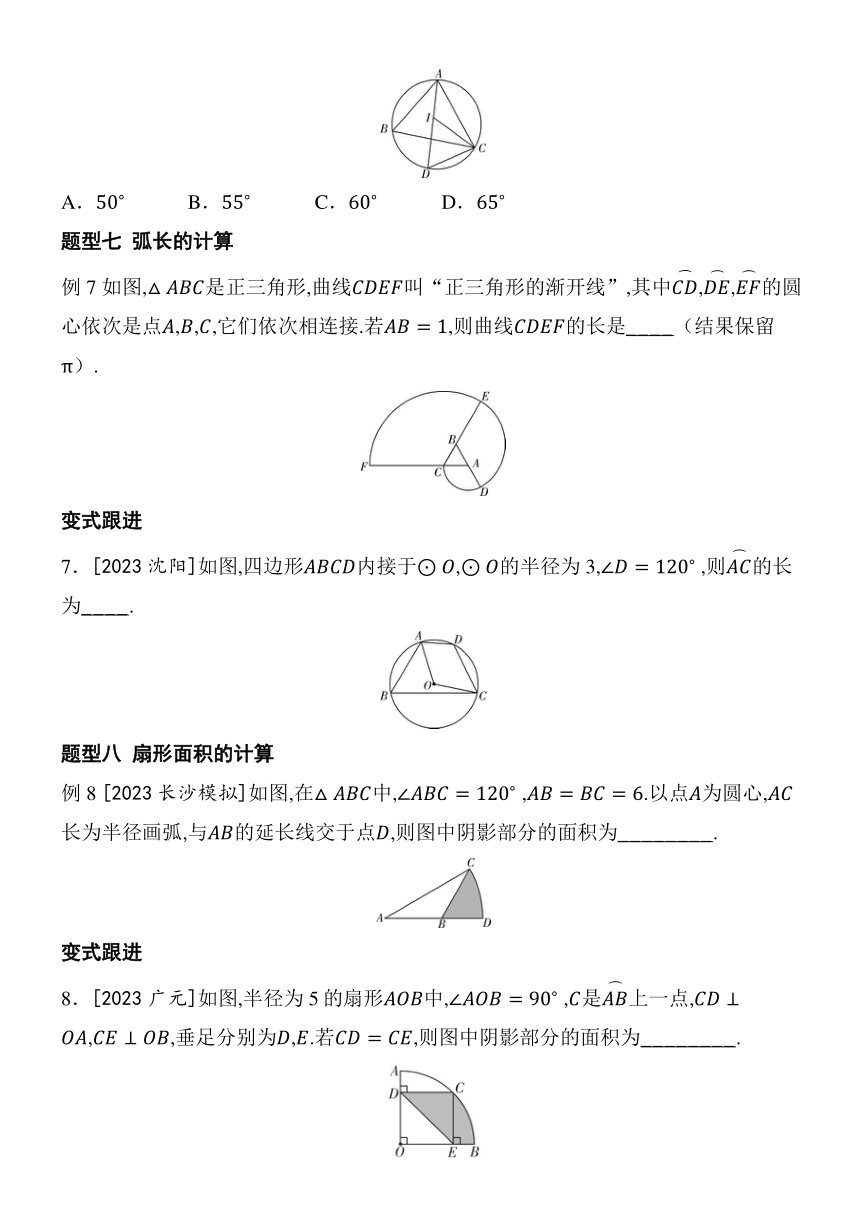
例7 如图,是正三角形,曲线叫“正三角形的渐开线”,其中,,的圆心依次是点,,,它们依次相连接.若,则曲线的长是_ _ _ _ (结果保留).
变式跟进
7.[2023沈阳]如图,四边形内接于,的半径为3, ,则的长为_ _ _ _ .
题型八 扇形面积的计算
例8 [2023长沙模拟]如图,在中, ,.以点为圆心,长为半径画弧,与的延长线交于点,则图中阴影部分的面积为_ _ _ _ _ _ _ _ .
变式跟进
8.[2023广元]如图,半径为5的扇形中, ,是上一点,,,垂足分别为,.若,则图中阴影部分的面积为_ _ _ _ _ _ _ _ .
题型九 圆锥的侧面积与全面积
例9 一个圆锥的底面半径,高,则这个圆锥的侧面积是( )
A. B. C. D.
变式跟进
9.如图,圆锥的底面半径为,母线长为,其侧面展开图是圆心角为 的扇形,则的长为( )
A. B. C. D.
过关训练 现复活用
A组·基础达标 逐点击破
1.下列说法不正确的是( )
A.直径是最长的弦
B.同圆中,所有的半径都相等
C.圆既是轴对称图形又是中心对称图形
D.长度相等的弧是等弧
2.[2024长沙模拟]如图,四边形内接于, 弦.若 ,则的度数为( )
A. B. C. D.
3.往直径为的圆柱形容器内装入一些水以后,截面如图所示.若水面宽,则水的最大深度为( )
A. B. C. D.
4.已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为 ,则扇形的面积是( )
A. B. C. D.
5.如图是一个隧道的横截面,它的形状是以点为圆心,为半径的圆的一部分,是中弦的中点,经过圆心交于点.若,则隧道的高(的长)为( )
A. B. C. D.
6.若扇形的圆心角为 ,半径为6,则该扇形的弧长为_ _ _ _ _ _ .
7.如图,的内切圆与三边分别相切于点,,.若 ,则_ _ _ _ _ _ .
8.[2024长沙模拟]如图,已知是的直径,弦,垂足为,且 ,,则图中阴影部分的面积为_ _ _ _ _ _ _ _ .
B组·能力提升 强化突破
9.[2023娄底]如图,正六边形的外接圆的半径为2,过圆心的两条直线,的夹角为 ,则图中的阴影部分的面积为( )
A. B. C. D.
10.如图,正方形的边长为8,是的中点,是边上的动点,连接,以点为圆心,的长为半径作.当与正方形的边相切时,的长为_ _ _ _ _ _ _ _ .
11.[2023长沙模拟]如图,在中,弦,相交于点,连接,.
(1) 求证:;
(2) 连接,,若,的半径为4,求的长.
12.如图①,为的直径,于点,,与相交于点.
① ②
(1) 求证:;
(2) 若,,求的长;
(3) 连接,,如图②,求证: .
专题4 圆
题型归类 举一反三
题型一 垂径定理及其推论
【点悟】 在已知直径与弦垂直的问题中,常连半径构造直角三角形,其中斜边为圆的半径,两直角边是弦长的一半和圆心到弦的距离,从而可以运用勾股定理来计算.
例1 D
变式跟进
1.B
题型二 圆周角定理的综合
【点悟】(1)在同圆(或等圆)中,圆心角(或圆周角)、弧、弦中只要有一组量相等,则其他对应的各组量也分别相等,利用这个性质可以将问题互相转化,达到求解或证明的目的.
(2)注意圆中的隐含条件(半径相等)的运用.
(3)圆周角定理及其推论是进行圆内角度转化与计算的主要依据,遇直径,要想到直径所对的圆周角是 ,从而得到直角三角形;遇弧所对的圆周角与圆心角,要想到同弧所对的圆心角等于圆周角的2倍以及同弧所对的圆周角相等.
例2
变式跟进
2.8
题型三 点和圆、直线和圆的位置关系
例3 C
变式跟进
3.D
题型四 切线的性质
例4 (1)
(2) 解:如答图,连接,.
是的直径,
,.
,.
,,
.
,.
,.
,,
,
,
的半径为6.
例4答图
变式跟进
4.(1) 证明:为的直径,为的切线,
,
.
,
,
.
,
.
(2) 解:如答图,连接.
为的中点,,
.
,
,
.
弦于点,为的直径,
.
变式跟进4答图
题型五 切线的判定
【点悟】 证明某直线为圆的切线时,如果已知直线与圆有公共点,即可作出过该点的半径,证明直线垂直于该半径,即“作半径,证垂直”;若不能确定某直线与已知圆有公共点,则过圆心作直线的垂线段,证明它到圆心的距离等于半径,即“作垂直,证半径”.证明垂直时,常用到“直径所对的圆周角是直角”.
例5 (1) 解:直线和相切.理由如下:
如答图,连接.
的平分线交于点,
.
,,
,.
,.
又是的半径,
直线和相切.
例5答图
(2) 的平分线交于点, ,,
,,
,,.
,
,.
,
,
解得,.
.
变式跟进
5.(1) 解:直线和相切.理由如下:
如答图,连接.
,,
,.
,,
.
, ,
,即 .
,
过圆心,
直线和相切.
变式跟进5答图
(2) , ,,
,,
即.
,
.
,
,
.
由勾股定理,得,
即,
解得(负值已舍),
.
题型六 切线长定理及三角形的内切圆
【点悟】(1)求解 三角形内切圆的问题时,常用到面积法:,其中 为 的内切圆半径,,,为 的三条边的长度;
(2)已知直角三角形的三边长,,(其中 为斜边),则内切圆半径;
(3)解决三角形与圆相切的问题时,常利用切线长定理及勾股定理等列方程(组)来求半径.
例6 C
变式跟进
6.C
题型七 弧长的计算
【点悟】 理解弧长公式 中各个量所代表的意义,是圆心角的度数,是扇形的半径,表示弧长.
例7
变式跟进
7.
题型八 扇形面积的计算
【点悟】 求不规则图形的面积时,常将其转化为易解决的基本图形,然后求出各图形的面积,通过面积的和差求出结果.
例8
变式跟进
8.
题型九 圆锥的侧面积与全面积
【点悟】(1)圆锥的侧面展开图是一个扇形;(2)圆锥的底面周长是其侧面展开图的弧长;(3)圆锥的母线就是其侧面展开图所得扇形的半径.
例9 C
变式跟进
9.A
过关训练 现复活用
A组·基础达标 逐点击破
1.D 2.B 3.C 4.C 5.D
6.
7.
8.
B组·能力提升 强化突破
9.C
10.3或
11.(1) 证明:,
,
,即,
.
(2) 解:,,
.
由圆周角定理,得 ,
的长为 .
第11题答图
12.(1) 证明:为的直径,于点,.
,,
,即,
.
(2) 解:如答图①,连接.
第12题答图①
由(1),得,,
,.
为的直径,于点,
.
设,则,
在中,,
即,
解得,的长为.
(3) 解:如答图②,连接,交于点.
,.
在和中,
,
,
.
,为的半径,
, ,
,
.
第12题答图②
题型归类 举一反三
题型一 垂径定理及其推论
例1 如图,的直径,弦,,垂足为,则的长为( )
A.5 B.6 C.7 D.8
变式跟进
1.如图,为的弦,为的中点,,,则的半径为( )
A.4 B.5 C.6 D.7
题型二 圆周角定理的综合
例2 如图,为的外接圆的直径,若 ,则_ _ _ _ _ _ .
变式跟进
2.[2023湘西模拟]如图,内接于, ,的平分线交于点.若,,则的长为_ _ .
题型三 点和圆、直线和圆的位置关系
例3 已知的半径为3,点在内,点到圆心的距离为,则的取值范围是( )
A. B. C. D.无法确定
变式跟进
3.如图,点,在半径为1的上, ,延长至点,过点作直线的垂线记为,则下列说法正确的是( )
A.当等于0.5时,和相离
B.当等于2时,和相切
C.当等于1时,和相交
D.当不等于1时,和不相切
题型四 切线的性质
例4 如图,在中,以为直径的交于点,与的延长线交于点,的切线与垂直,垂足为.
(1) 与的数量关系是_ _ _ _ _ _ _ _ ;
(2) 若,,求的半径.
变式跟进
4.[2023长沙模拟]如图,以的边为直径作,交边于点,为的切线,弦于点,连接.
(1) 求证:;
(2) 若为的中点,且,求线段的长.
题型五 切线的判定
例5 [2023长沙模拟]如图,为的直径,为上一点,的平分线交于点,于点.
(1) 试判断直线和的位置关系,并说明理由;
(2) 过点作于点,若 ,,求图中阴影部分的面积.
变式跟进
5.[2023长沙模拟]如图,是的弦,是外一点,,交于点,交于点,且.
(1) 判断直线和的位置关系,并说明理由;
(2) 若 ,,求图中阴影部分的面积.
题型六 切线长定理及三角形的内切圆
例6 《九章算术》是我国古代内容极为丰富的数学著作.书中有下列问题:“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)的直径是多少?( )
A.3步 B.5步 C.6步 D.8步
变式跟进
6.如图,在中, , ,是的内心,延长交的外接圆于点,则的度数是( )
A. B. C. D.
题型七 弧长的计算
例7 如图,是正三角形,曲线叫“正三角形的渐开线”,其中,,的圆心依次是点,,,它们依次相连接.若,则曲线的长是_ _ _ _ (结果保留).
变式跟进
7.[2023沈阳]如图,四边形内接于,的半径为3, ,则的长为_ _ _ _ .
题型八 扇形面积的计算
例8 [2023长沙模拟]如图,在中, ,.以点为圆心,长为半径画弧,与的延长线交于点,则图中阴影部分的面积为_ _ _ _ _ _ _ _ .
变式跟进
8.[2023广元]如图,半径为5的扇形中, ,是上一点,,,垂足分别为,.若,则图中阴影部分的面积为_ _ _ _ _ _ _ _ .
题型九 圆锥的侧面积与全面积
例9 一个圆锥的底面半径,高,则这个圆锥的侧面积是( )
A. B. C. D.
变式跟进
9.如图,圆锥的底面半径为,母线长为,其侧面展开图是圆心角为 的扇形,则的长为( )
A. B. C. D.
过关训练 现复活用
A组·基础达标 逐点击破
1.下列说法不正确的是( )
A.直径是最长的弦
B.同圆中,所有的半径都相等
C.圆既是轴对称图形又是中心对称图形
D.长度相等的弧是等弧
2.[2024长沙模拟]如图,四边形内接于, 弦.若 ,则的度数为( )
A. B. C. D.
3.往直径为的圆柱形容器内装入一些水以后,截面如图所示.若水面宽,则水的最大深度为( )
A. B. C. D.
4.已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为 ,则扇形的面积是( )
A. B. C. D.
5.如图是一个隧道的横截面,它的形状是以点为圆心,为半径的圆的一部分,是中弦的中点,经过圆心交于点.若,则隧道的高(的长)为( )
A. B. C. D.
6.若扇形的圆心角为 ,半径为6,则该扇形的弧长为_ _ _ _ _ _ .
7.如图,的内切圆与三边分别相切于点,,.若 ,则_ _ _ _ _ _ .
8.[2024长沙模拟]如图,已知是的直径,弦,垂足为,且 ,,则图中阴影部分的面积为_ _ _ _ _ _ _ _ .
B组·能力提升 强化突破
9.[2023娄底]如图,正六边形的外接圆的半径为2,过圆心的两条直线,的夹角为 ,则图中的阴影部分的面积为( )
A. B. C. D.
10.如图,正方形的边长为8,是的中点,是边上的动点,连接,以点为圆心,的长为半径作.当与正方形的边相切时,的长为_ _ _ _ _ _ _ _ .
11.[2023长沙模拟]如图,在中,弦,相交于点,连接,.
(1) 求证:;
(2) 连接,,若,的半径为4,求的长.
12.如图①,为的直径,于点,,与相交于点.
① ②
(1) 求证:;
(2) 若,,求的长;
(3) 连接,,如图②,求证: .
专题4 圆
题型归类 举一反三
题型一 垂径定理及其推论
【点悟】 在已知直径与弦垂直的问题中,常连半径构造直角三角形,其中斜边为圆的半径,两直角边是弦长的一半和圆心到弦的距离,从而可以运用勾股定理来计算.
例1 D
变式跟进
1.B
题型二 圆周角定理的综合
【点悟】(1)在同圆(或等圆)中,圆心角(或圆周角)、弧、弦中只要有一组量相等,则其他对应的各组量也分别相等,利用这个性质可以将问题互相转化,达到求解或证明的目的.
(2)注意圆中的隐含条件(半径相等)的运用.
(3)圆周角定理及其推论是进行圆内角度转化与计算的主要依据,遇直径,要想到直径所对的圆周角是 ,从而得到直角三角形;遇弧所对的圆周角与圆心角,要想到同弧所对的圆心角等于圆周角的2倍以及同弧所对的圆周角相等.
例2
变式跟进
2.8
题型三 点和圆、直线和圆的位置关系
例3 C
变式跟进
3.D
题型四 切线的性质
例4 (1)
(2) 解:如答图,连接,.
是的直径,
,.
,.
,,
.
,.
,.
,,
,
,
的半径为6.
例4答图
变式跟进
4.(1) 证明:为的直径,为的切线,
,
.
,
,
.
,
.
(2) 解:如答图,连接.
为的中点,,
.
,
,
.
弦于点,为的直径,
.
变式跟进4答图
题型五 切线的判定
【点悟】 证明某直线为圆的切线时,如果已知直线与圆有公共点,即可作出过该点的半径,证明直线垂直于该半径,即“作半径,证垂直”;若不能确定某直线与已知圆有公共点,则过圆心作直线的垂线段,证明它到圆心的距离等于半径,即“作垂直,证半径”.证明垂直时,常用到“直径所对的圆周角是直角”.
例5 (1) 解:直线和相切.理由如下:
如答图,连接.
的平分线交于点,
.
,,
,.
,.
又是的半径,
直线和相切.
例5答图
(2) 的平分线交于点, ,,
,,
,,.
,
,.
,
,
解得,.
.
变式跟进
5.(1) 解:直线和相切.理由如下:
如答图,连接.
,,
,.
,,
.
, ,
,即 .
,
过圆心,
直线和相切.
变式跟进5答图
(2) , ,,
,,
即.
,
.
,
,
.
由勾股定理,得,
即,
解得(负值已舍),
.
题型六 切线长定理及三角形的内切圆
【点悟】(1)求解 三角形内切圆的问题时,常用到面积法:,其中 为 的内切圆半径,,,为 的三条边的长度;
(2)已知直角三角形的三边长,,(其中 为斜边),则内切圆半径;
(3)解决三角形与圆相切的问题时,常利用切线长定理及勾股定理等列方程(组)来求半径.
例6 C
变式跟进
6.C
题型七 弧长的计算
【点悟】 理解弧长公式 中各个量所代表的意义,是圆心角的度数,是扇形的半径,表示弧长.
例7
变式跟进
7.
题型八 扇形面积的计算
【点悟】 求不规则图形的面积时,常将其转化为易解决的基本图形,然后求出各图形的面积,通过面积的和差求出结果.
例8
变式跟进
8.
题型九 圆锥的侧面积与全面积
【点悟】(1)圆锥的侧面展开图是一个扇形;(2)圆锥的底面周长是其侧面展开图的弧长;(3)圆锥的母线就是其侧面展开图所得扇形的半径.
例9 C
变式跟进
9.A
过关训练 现复活用
A组·基础达标 逐点击破
1.D 2.B 3.C 4.C 5.D
6.
7.
8.
B组·能力提升 强化突破
9.C
10.3或
11.(1) 证明:,
,
,即,
.
(2) 解:,,
.
由圆周角定理,得 ,
的长为 .
第11题答图
12.(1) 证明:为的直径,于点,.
,,
,即,
.
(2) 解:如答图①,连接.
第12题答图①
由(1),得,,
,.
为的直径,于点,
.
设,则,
在中,,
即,
解得,的长为.
(3) 解:如答图②,连接,交于点.
,.
在和中,
,
,
.
,为的半径,
, ,
,
.
第12题答图②
同课章节目录
