16.1.2 幂的乘方与积的乘方 教案 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 16.1.2 幂的乘方与积的乘方 教案 2025-2026学年数学人教版八年级上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 115.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 00:00:00 | ||
图片预览

文档简介
16.1.2 幂的乘方与积的乘方
【素养目标】
1.探究并证明幂的乘方与积的乘方性质;
2.会运用幂的乘方与积的乘方性质进行计算;
3.在类比同底数幂的乘法性质学习幂的乘方与积的乘方性质时,体会三者的联系和区别及类比、归纳的思想方法.
【教学重点】
幂的乘方与积的乘方的运算性质.
【教学难点】
区别同底数幂、幂的乘方、积的乘方的运算性质.
【教学过程】
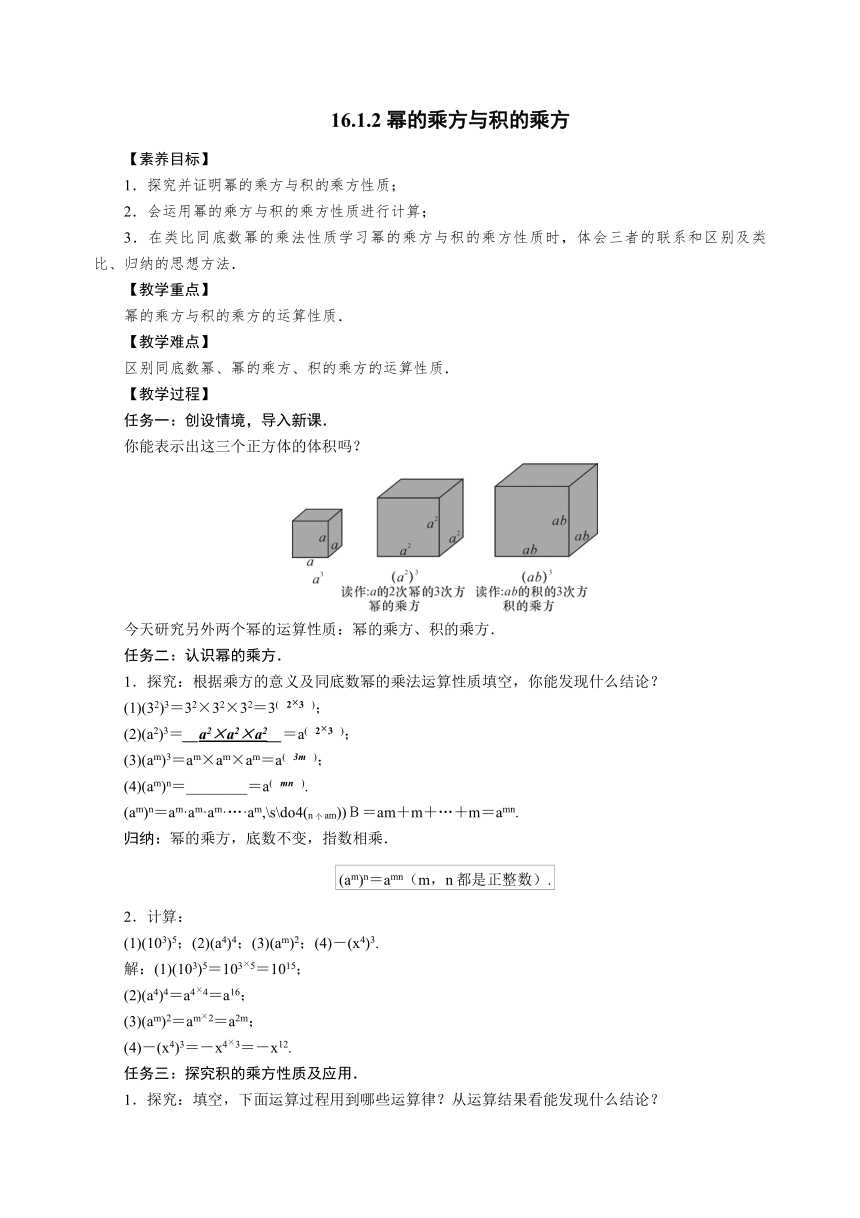
任务一:创设情境,导入新课.
你能表示出这三个正方体的体积吗?
今天研究另外两个幂的运算性质:幂的乘方、积的乘方.
任务二:认识幂的乘方.
1.探究:根据乘方的意义及同底数幂的乘法运算性质填空,你能发现什么结论?
(1)(32)3=32×32×32=3( 2×3 );
(2)(a2)3=__a2×a2×a2__=a( 2×3 );
(3)(am)3=am×am×am=a( 3m );
(4)(am)n=________=a( mn ).
(am)n=am·am·am·…·am,\s\do4(n个am))B=am+m+…+m=amn.
归纳:幂的乘方,底数不变,指数相乘.
2.计算:
(1)(103)5;(2)(a4)4;(3)(am)2;(4)-(x4)3.
解:(1)(103)5=103×5=1015;
(2)(a4)4=a4×4=a16;
(3)(am)2=am×2=a2m;
(4)-(x4)3=-x4×3=-x12.
任务三:探究积的乘方性质及应用.
1.探究:填空,下面运算过程用到哪些运算律?从运算结果看能发现什么结论?
(1)(ab)2=ab·ab=(a·a)(b·b)=a( 2 )b( 2 );
(2)(ab)3=ab·ab·ab=(a·a·a)(b·b·b)=a( 3 )b( 3 );
(3)(ab)n=a( )b( ).
(ab)n=(ab)·(ab)·…·(ab)=(a·a·…·a)·(b·b·…·b)=anbn.
归纳:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
2.计算:
(1)(2a)3;(2)(-5b)3;(3)(xy2)2;(4)(-2x3)4.
提示:先确定底数有哪几个因式(数).
解:(1)原式=23×a3=8a3;
(2)原式=(-5)3×b3=-125b3;
(3)原式=x2(y2)2=x2y4;[(y2)2表示幂的乘方]
(4)原式=(-2)4×(x3)4=16x12.[(x3)4表示幂的乘方]
3.计算:(-3a3)2·a4
(-3a3)2·a4
↓
=[(-3)2×(a3)2]·a4
↓
=9a6·a4
↓
=9a10
任务四:尝试练习,巩固内化.
解答教材P101练习1、2、3.
任务五:课堂小结,形成体系.
1.反思与交流:
完成今天的学习后,你学到了什么呢?你能解决什么样的问题呢?你还有疑问吗?
2.知识结构:
幂的运算性质
am·an=am+n
(am)n=amn
(ab)n=an·bn
【布置作业】
教材P101-P102习题16.1,第2~9题.
【教学反思】
新版教材把“幂的乘方”和“积的乘方”合成一个课时,因为探究它们的性质的过程和方法与“同底数幂的乘法”一样,但增加了区别同底数幂、幂的乘方、积的乘方的运算性质的难度,所以在“任务三:探究积的乘方性质及应用”中专门设置了“计算:(-3a3)2·a4”,意在区分三种幂的运算和它们的性质.
【素养目标】
1.探究并证明幂的乘方与积的乘方性质;
2.会运用幂的乘方与积的乘方性质进行计算;
3.在类比同底数幂的乘法性质学习幂的乘方与积的乘方性质时,体会三者的联系和区别及类比、归纳的思想方法.
【教学重点】
幂的乘方与积的乘方的运算性质.
【教学难点】
区别同底数幂、幂的乘方、积的乘方的运算性质.
【教学过程】
任务一:创设情境,导入新课.
你能表示出这三个正方体的体积吗?
今天研究另外两个幂的运算性质:幂的乘方、积的乘方.
任务二:认识幂的乘方.
1.探究:根据乘方的意义及同底数幂的乘法运算性质填空,你能发现什么结论?
(1)(32)3=32×32×32=3( 2×3 );
(2)(a2)3=__a2×a2×a2__=a( 2×3 );
(3)(am)3=am×am×am=a( 3m );
(4)(am)n=________=a( mn ).
(am)n=am·am·am·…·am,\s\do4(n个am))B=am+m+…+m=amn.
归纳:幂的乘方,底数不变,指数相乘.
2.计算:
(1)(103)5;(2)(a4)4;(3)(am)2;(4)-(x4)3.
解:(1)(103)5=103×5=1015;
(2)(a4)4=a4×4=a16;
(3)(am)2=am×2=a2m;
(4)-(x4)3=-x4×3=-x12.
任务三:探究积的乘方性质及应用.
1.探究:填空,下面运算过程用到哪些运算律?从运算结果看能发现什么结论?
(1)(ab)2=ab·ab=(a·a)(b·b)=a( 2 )b( 2 );
(2)(ab)3=ab·ab·ab=(a·a·a)(b·b·b)=a( 3 )b( 3 );
(3)(ab)n=a( )b( ).
(ab)n=(ab)·(ab)·…·(ab)=(a·a·…·a)·(b·b·…·b)=anbn.
归纳:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
2.计算:
(1)(2a)3;(2)(-5b)3;(3)(xy2)2;(4)(-2x3)4.
提示:先确定底数有哪几个因式(数).
解:(1)原式=23×a3=8a3;
(2)原式=(-5)3×b3=-125b3;
(3)原式=x2(y2)2=x2y4;[(y2)2表示幂的乘方]
(4)原式=(-2)4×(x3)4=16x12.[(x3)4表示幂的乘方]
3.计算:(-3a3)2·a4
(-3a3)2·a4
↓
=[(-3)2×(a3)2]·a4
↓
=9a6·a4
↓
=9a10
任务四:尝试练习,巩固内化.
解答教材P101练习1、2、3.
任务五:课堂小结,形成体系.
1.反思与交流:
完成今天的学习后,你学到了什么呢?你能解决什么样的问题呢?你还有疑问吗?
2.知识结构:
幂的运算性质
am·an=am+n
(am)n=amn
(ab)n=an·bn
【布置作业】
教材P101-P102习题16.1,第2~9题.
【教学反思】
新版教材把“幂的乘方”和“积的乘方”合成一个课时,因为探究它们的性质的过程和方法与“同底数幂的乘法”一样,但增加了区别同底数幂、幂的乘方、积的乘方的运算性质的难度,所以在“任务三:探究积的乘方性质及应用”中专门设置了“计算:(-3a3)2·a4”,意在区分三种幂的运算和它们的性质.
同课章节目录
