16.2.3 多项式乘多项式 教案 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 16.2.3 多项式乘多项式 教案 2025-2026学年数学人教版八年级上册 | 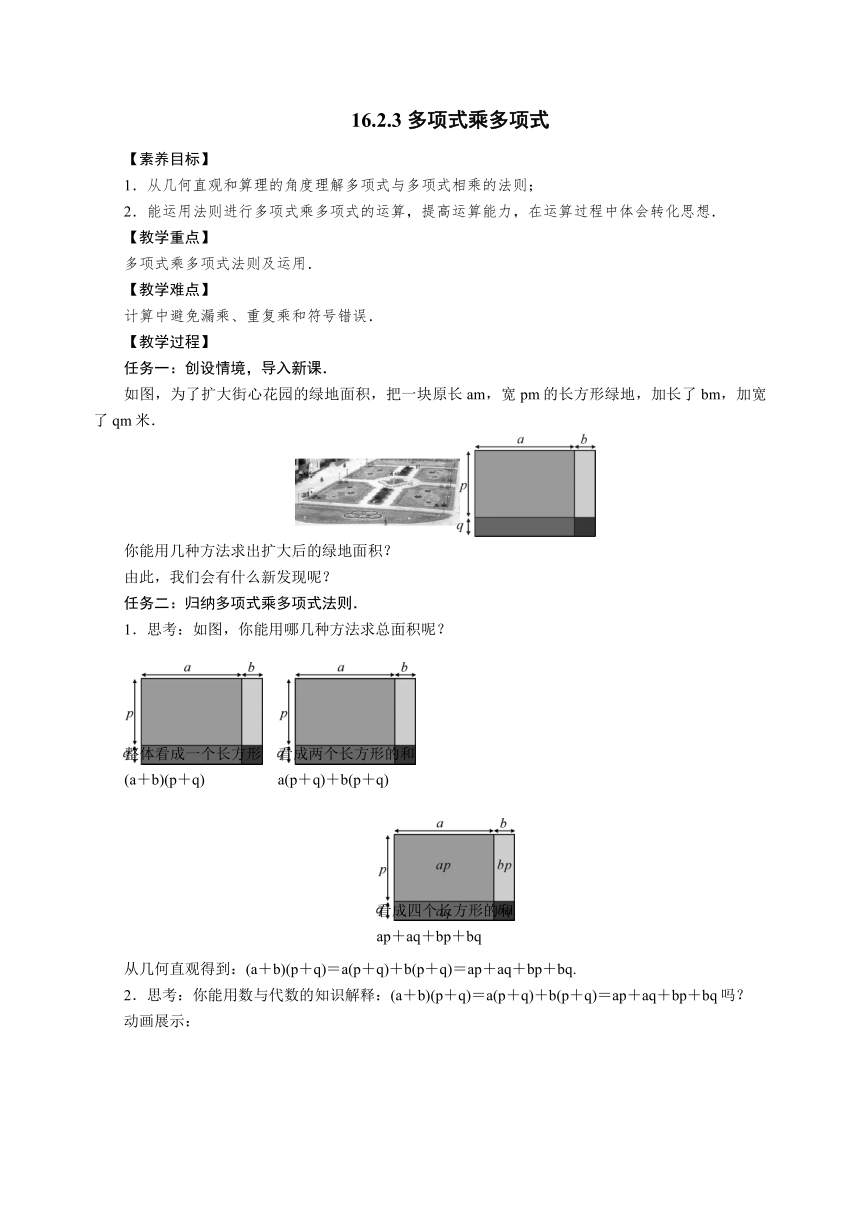 | |
| 格式 | doc | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 23:40:20 | ||
图片预览

文档简介
16.2.3 多项式乘多项式
【素养目标】
1.从几何直观和算理的角度理解多项式与多项式相乘的法则;
2.能运用法则进行多项式乘多项式的运算,提高运算能力,在运算过程中体会转化思想.
【教学重点】
多项式乘多项式法则及运用.
【教学难点】
计算中避免漏乘、重复乘和符号错误.
【教学过程】
任务一:创设情境,导入新课.
如图,为了扩大街心花园的绿地面积,把一块原长am,宽pm的长方形绿地,加长了bm,加宽了qm米.
你能用几种方法求出扩大后的绿地面积?
由此,我们会有什么新发现呢?
任务二:归纳多项式乘多项式法则.
1.思考:如图,你能用哪几种方法求总面积呢?
eq \o(\s\up7(),\s\do5(\a\vs4\al(整体看成一个长方形,(a+b)(p+q)))) eq \o(\s\up7(),\s\do5(\a\vs4\al(看成两个长方形的和,a(p+q)+b(p+q))))
eq \o(\s\up7(),\s\do5(\a\vs4\al(看成四个长方形的和,ap+aq+bp+bq)))
从几何直观得到:(a+b)(p+q)=a(p+q)+b(p+q)=ap+aq+bp+bq.
2.思考:你能用数与代数的知识解释:(a+b)(p+q)=a(p+q)+b(p+q)=ap+aq+bp+bq吗?
动画展示:
3.思考:(a+b)(p+q)中,(a+b)和(p+q)都是多项式,
从(a+b)(p+q)=ap+aq+bp+bq你能发现多项式乘多项式的方法吗?
动画展示:
归纳:多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
任务三:运用法则进行多项式乘多项式运算.
1.计算:
(1)(a+3)(a-2);(2)(3x+1)(x+2).
解:(1)(a+3)(a-2)(确定多项式的项,每一项包括前面的符号.)
=a·a+a·(-2)+3·a+3×(-2)(回头检查符号;是否漏乘.)
=a2-2a+3a-6(合并同类项.)
=a2+a-6;
(2)(3x+1)(x+2)
=3x·x+3x·2+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2.
2.计算:
(1)(x-8y)(x-y);
(2)(x+y)(x2-xy+y2).
解:(1)(x-8y)(x-y)(确定多项式的项,每一项包括前面的符号.)
=x·x-xy-8xy+8y2(回头检查符号;是否漏乘.)
=x2-9xy+8y2;
(2)(x+y)(x2-xy+y2)
=x·x2-x·xy+xy2+y·x2-y·xy+y·y2(二项式乘三项式得6项.)
=x3-x2y+xy2+x2y-xy2+y3
=x3+y3.
任务四:尝试练习,巩固内化.
解答教材P107练习1、2、3.
任务五:课堂小结,形成体系.
1.反思与交流:
完成今天的学习后,你学到了什么呢?你能解决什么样的问题呢?你还有疑问吗?
2.知识结构:
幂的运算性质
am·an=am+n
(am)n=amn
(ab)n=an·bn→—
【布置作业】
教材P110-P111习题16.2,第3、5(2)(3)、11题.
【教学反思】
多项式乘多项式运算是本章的重点,多项式乘多项式转化成单项式乘多项式、单项式乘单项式,最后转化成幂的运算,它是前几节各种性质、法则的综合运用.
计算正确在此达到最大难度,避免漏乘、重复乘和符号错误成为关键,克服错误的方法需要学生主动体验,如不省步骤,确定多项式的项(包括前面的符号),一步一回头检查等,也需要教师在课堂上介绍、推荐.
【素养目标】
1.从几何直观和算理的角度理解多项式与多项式相乘的法则;
2.能运用法则进行多项式乘多项式的运算,提高运算能力,在运算过程中体会转化思想.
【教学重点】
多项式乘多项式法则及运用.
【教学难点】
计算中避免漏乘、重复乘和符号错误.
【教学过程】
任务一:创设情境,导入新课.
如图,为了扩大街心花园的绿地面积,把一块原长am,宽pm的长方形绿地,加长了bm,加宽了qm米.
你能用几种方法求出扩大后的绿地面积?
由此,我们会有什么新发现呢?
任务二:归纳多项式乘多项式法则.
1.思考:如图,你能用哪几种方法求总面积呢?
eq \o(\s\up7(),\s\do5(\a\vs4\al(整体看成一个长方形,(a+b)(p+q)))) eq \o(\s\up7(),\s\do5(\a\vs4\al(看成两个长方形的和,a(p+q)+b(p+q))))
eq \o(\s\up7(),\s\do5(\a\vs4\al(看成四个长方形的和,ap+aq+bp+bq)))
从几何直观得到:(a+b)(p+q)=a(p+q)+b(p+q)=ap+aq+bp+bq.
2.思考:你能用数与代数的知识解释:(a+b)(p+q)=a(p+q)+b(p+q)=ap+aq+bp+bq吗?
动画展示:
3.思考:(a+b)(p+q)中,(a+b)和(p+q)都是多项式,
从(a+b)(p+q)=ap+aq+bp+bq你能发现多项式乘多项式的方法吗?
动画展示:
归纳:多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
任务三:运用法则进行多项式乘多项式运算.
1.计算:
(1)(a+3)(a-2);(2)(3x+1)(x+2).
解:(1)(a+3)(a-2)(确定多项式的项,每一项包括前面的符号.)
=a·a+a·(-2)+3·a+3×(-2)(回头检查符号;是否漏乘.)
=a2-2a+3a-6(合并同类项.)
=a2+a-6;
(2)(3x+1)(x+2)
=3x·x+3x·2+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2.
2.计算:
(1)(x-8y)(x-y);
(2)(x+y)(x2-xy+y2).
解:(1)(x-8y)(x-y)(确定多项式的项,每一项包括前面的符号.)
=x·x-xy-8xy+8y2(回头检查符号;是否漏乘.)
=x2-9xy+8y2;
(2)(x+y)(x2-xy+y2)
=x·x2-x·xy+xy2+y·x2-y·xy+y·y2(二项式乘三项式得6项.)
=x3-x2y+xy2+x2y-xy2+y3
=x3+y3.
任务四:尝试练习,巩固内化.
解答教材P107练习1、2、3.
任务五:课堂小结,形成体系.
1.反思与交流:
完成今天的学习后,你学到了什么呢?你能解决什么样的问题呢?你还有疑问吗?
2.知识结构:
幂的运算性质
am·an=am+n
(am)n=amn
(ab)n=an·bn→—
【布置作业】
教材P110-P111习题16.2,第3、5(2)(3)、11题.
【教学反思】
多项式乘多项式运算是本章的重点,多项式乘多项式转化成单项式乘多项式、单项式乘单项式,最后转化成幂的运算,它是前几节各种性质、法则的综合运用.
计算正确在此达到最大难度,避免漏乘、重复乘和符号错误成为关键,克服错误的方法需要学生主动体验,如不省步骤,确定多项式的项(包括前面的符号),一步一回头检查等,也需要教师在课堂上介绍、推荐.
同课章节目录
