1.1 第一课时 菱形的性质 教学课件(共39张PPT)2025-2026学年北师大版九年级数学上册
文档属性
| 名称 | 1.1 第一课时 菱形的性质 教学课件(共39张PPT)2025-2026学年北师大版九年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 15.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-11 15:06:26 | ||
图片预览





文档简介
(共39张PPT)
第一章 特殊平行四边形
1.1 菱形的性质与判定
第1课时 菱形的性质
情景导入
欣赏下面图片,图片中框出的图形是你熟悉的吗?
欣赏视频,前面的图片中出现的图形是平行四边形,和视频中菱形一致,那么什么是菱形呢?
点击图片,播放视频
实践探究
探究1:菱形的性质
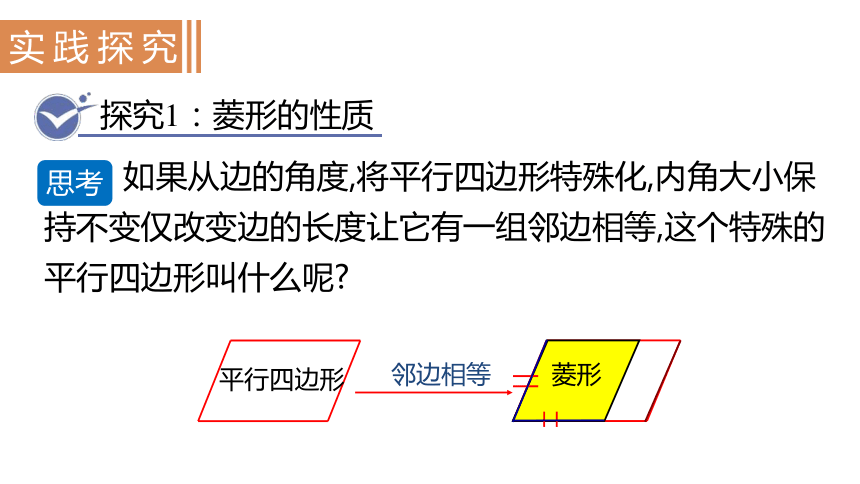
如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
菱形
邻边相等
思考
归纳总结
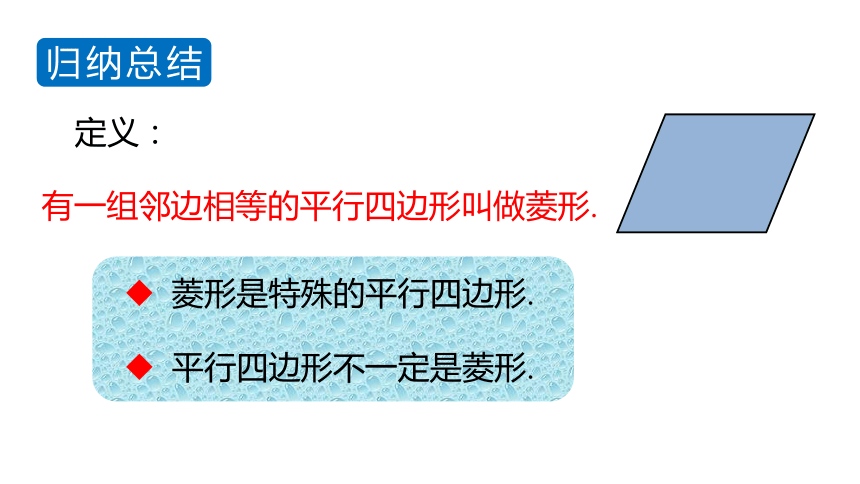
定义:
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
有一组邻边相等的平行四边形叫做菱形.
(1)菱形是特殊的平行四边形,它具有一般平行四边形的所有性质,你能列举一些这样的性质吗?
(2)你认为菱形还具有哪些特殊的性质?
思考
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
点击图片,播放视频
活动1
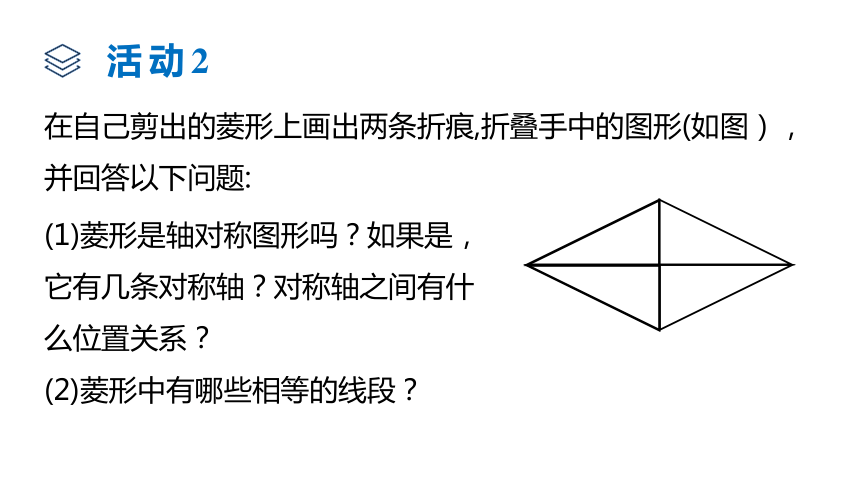
在自己剪出的菱形上画出两条折痕,折叠手中的图形(如图),并回答以下问题:
(1)菱形是轴对称图形吗?如果是,它有几条对称轴?对称轴之间有什么位置关系?
(2)菱形中有哪些相等的线段?
活动2
归纳总结
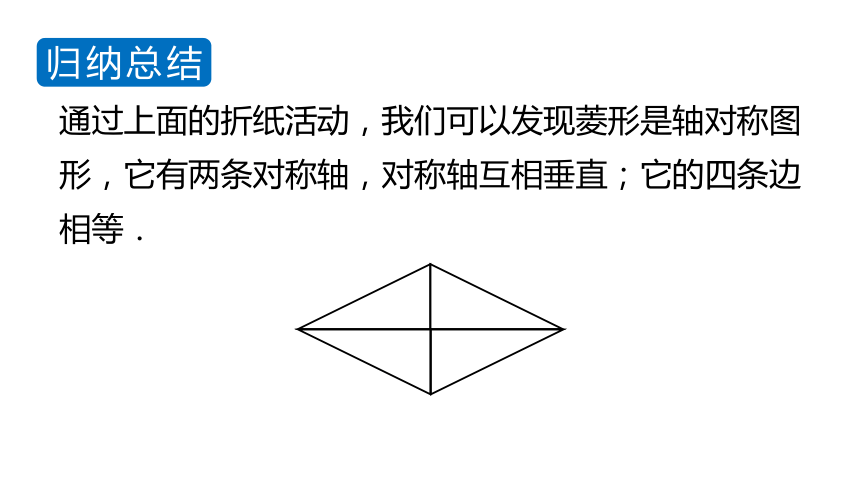
通过上面的折纸活动,我们可以发现菱形是轴对称图形,它有两条对称轴,对称轴互相垂直;它的四条边相等.
探究2
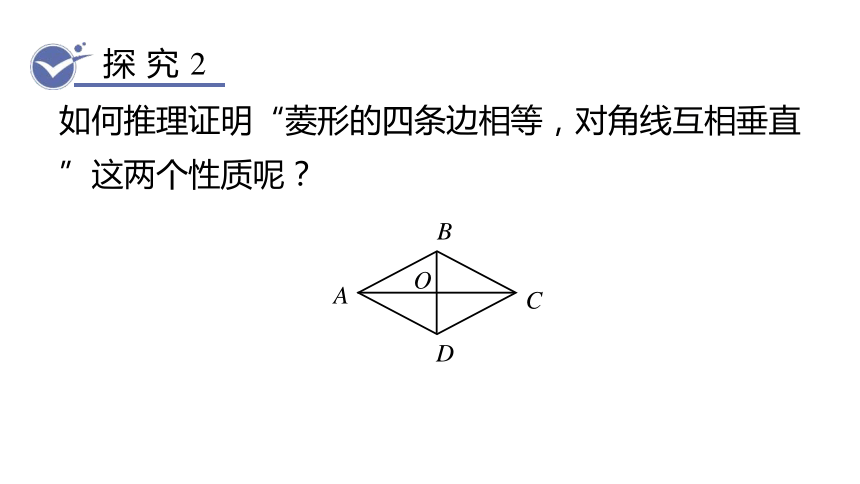
如何推理证明“菱形的四条边相等,对角线互相垂直”这两个性质呢?
A
B
C
O
D
已知:如图,在平行四边形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:(1) AB = BC = CD =AD;
(2) AC⊥BD;
A
B
C
O
D
思考:(1)菱形是特殊的平行四边形,你能从平行四边形的性质证明菱形的四条边相等吗?
(2)可以利用什么性质来证明AC⊥BD.
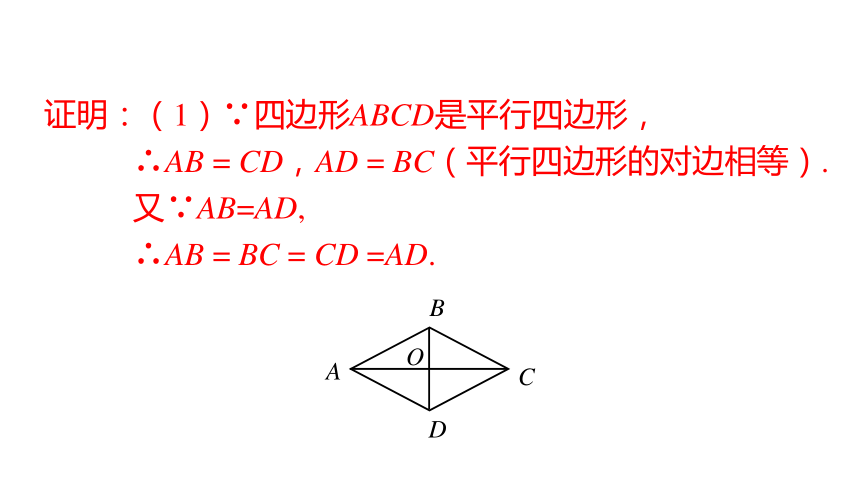
证明:(1)∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC(平行四边形的对边相等).
又∵AB=AD,
∴AB = BC = CD =AD.
A
B
C
O
D
(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB = OD (菱形的对角线互相平分).
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,
即AC⊥BD.
A
B
C
O
D
归纳
定理 菱形的四条边相等;
定理 菱形的对角线相互垂直.
探究3:定理的拓展延伸
过对“菱形的对角线互相垂直”的证明过程,你还能发现菱形的对角线有什么性质?
方法提示:由折叠过程或等腰三角形“三线合一”推出菱形对角线的性质.
归纳
菱形的每条对角线平分一组对角.
菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
角:对角相等.
边:对边平行且相等.
对角线:相互平分.
菱形的特殊性质
平行四边形的性质
归纳总结
对称性:是轴对称图形.
边:四条边都相等.
对角线:互相垂直,且每条对角线平分一组对角.
应用举例
如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD=6,求菱形的边长AB和对角线AC的长.
例1
解:∵四边形ABCD是菱形,
∴AB=AD(菱形的四条边都相等),AC⊥BD(菱形的对角线互相垂直),
OB=OD= BD= ×6=3(菱形的对角线互相平分).
在等腰△ABD中,∵∠BAD=60°,
∴△ABD是等边三角形,
∴AB=BD=6.
在Rt△AOB中,由勾股定理得OA2+OB2=AB2,
∴OA= ,∴AC=2OA= .
如图,在菱形ABCD中,∠ABC=60°,DE∥AC且交BC的延长线于点E.
求证:DE= BE.
例2
【方法指导】连接BD,由四边形ABCD是菱形,∠ABC=60°,易得BD⊥AC,∠DBC=30°,又由DE∥AC,即可证得DE⊥BD,由30°所对的直角边等于斜边的一半,即可证得DE= BE.
A
B
C
D
E
证明:连接BD.
∵四边形ABCD是菱形,∠ABC=60°,
∴BD⊥AC,∠DBE=30°.
∵DE∥AC,
∴DE⊥BD,即∠BDE=90°.
∵在Rt△BDE中,∠DBE=30°,
∴DE= BE.
A
B
C
D
E
课堂小结
菱形的性质
菱形的性质
有关计算
边
周长=边长的四倍
角
对角线
1.两组对边平行且相等
2.四条边相等
两组对角分别相等,邻角互补邻角互补
1.两条对角线互相垂直平分
2.每一条对角线平分一组对角
随堂练习
知识点1 菱形的定义及对称性
1.下列说法正确的是( )
A.两组对边分别相等的四边形是菱形
B.两组对角分别相等的四边形是菱形
C.一组邻边相等的平行四边形是菱形
D.一组对边平行且相等的四边形是菱形
C
2.如图,在菱形OABC中,若点B在x轴上,点A的坐标为(3,5),则点C的坐标为___________.
(3,-5)
知识点2 菱形的边、角的性质
3.在菱形ABCD 中,若AB=6,则菱形ABCD 的周长为( )
A.6 B.12
C.24 D.48
C
4.如图,已知菱形ABCD.
(1)若∠B=70°,则∠BAC的度数是_______;
(2)若AB=10,∠B=60°,则AC的长为______.
55°
10
5.(教材P9习题T1变式)如图,在菱形ABCD中,点E,F分别在边BC和CD上,且∠AEB=∠AFD.求证:BE=DF.
证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
在△ABE和△ADF中,
∵∠AEB=∠AFD,∠B=∠D,AB=AD,
∴△ABE≌△ADF(AAS),∴BE=DF.
知识点3 菱形的对角线的性质
6.如图,四边形ABCD为菱形,下列描述不一定正确的是( )
A.CA平分∠BCD
B.AC,BD互相平分
C.∠AOB=90°
D.AC=CD
D
7.【新情境·传统文化】中国结寓意团圆、美满,以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴.如图,小陶家有一个中国结装饰,可以近似地看作菱形ABCD,测得BD=16 cm,AC=12 cm,则此菱形的周长为( )
A.28 cm B.40 cm
C.56 cm D.80 cm
B
8.如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )
A. B.1
C. D.
D
[变式](2025·鞍山岫岩月考)如图,在菱形ABCD中,∠A=60°,AD=4,P是边AB上的一个动点,E,F分别是DP,BP的中点,则线段EF的长为( )
A.2 B.4
C.2 D.2
A
9.如图,在平面直角坐标系xOy中,四边形ABCD是菱形,A,B两点的坐标分别是(2,2),(-1,-),点D在第一象限,则点D的坐标是( )
A.(6,2) B.(8,2)
C.(6,) D.(8,)
B
10.(教材P9习题T3变式)如图,四边形ABCD是菱形,CD=5,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6
C. D.12
A
11.如图,在菱形ABCD中,AB的垂直平分线FE交对角线AC于点F,交AB于点E,连接DF.
(1)求证:AF=DF;
解:证明:如图,连接BF.
∵EF垂直平分AB,
∴AF=BF.
∵四边形ABCD是菱形,
∴AD=AB,∠DAF=∠BAF.
又∵AF=AF,
∴△DAF≌△BAF(SAS),
∴DF=BF,
∴AF=DF.
11.如图,在菱形ABCD中,AB的垂直平分线FE交对角线AC于点F,交AB于点E,连接DF.
(2)若∠BAD=70°,求∠FDC的度数.
解:证明:∵四边形ABCD是菱形,∠BAD=70°,
∴∠DAF=∠BAD=35°,
∠ADC=180°-∠BAD=110°.
∵AF=DF,
∴∠ADF=∠DAF=35°,
∴∠FDC=∠ADC-∠ADF=110°-35°=75°.
12.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且点E,F不与点B,C,D重合.
(1)求证:不论点E,F在BC,CD上如何滑动,总有BE=CF.
解:证明:如图,连接AC.
∵四边形ABCD是菱形,∠BAD=120°,
∴∠BAC=∠ACD=∠ABC=∠ACB=60°,
∴∠1+∠EAC=60°,AB=AC.
∵△AEF为等边三角形,
∴∠EAF=∠2+∠EAC=60°,
∴BE=CF.
∴∠1=∠2.
在△ABE和△ACF中,
∵∠1=∠2,AB=AC,∠ABC=∠ACD,
∴△ABE≌△ACF(ASA),
∴BE=CF.
12.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且点E,F不与点B,C,D重合.
(2)点E,F在BC,CD上滑动的过程中,四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.
解:证明:四边形AECF的面积不变,
△CEF的周长发生变化.
由(1),得△ABE≌△ACF,
∴S△ABE=S△ACF,
∴S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值.
过点A作AH⊥BC于点H(图略),则∠AHB=90°.
在Rt△ABH中,∠AHB=90°.
∵∠ABC=60°,∴∠BAH=30°.
∵AB=4,∴BC=4,BH=AB=2,
∴S四边形AECF=S△ABC=BC·AH=BC·
=4.
∵△CEF的周长为CE+CF+EF=CE+BE+
EF=BC+EF=BC+AE,
由“垂线段最短”可知,当等边三角形AEF的边AE与BC垂直时,边AE最短,
∴△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长最小,最小值为4+=4+2.
第一章 特殊平行四边形
1.1 菱形的性质与判定
第1课时 菱形的性质
情景导入
欣赏下面图片,图片中框出的图形是你熟悉的吗?
欣赏视频,前面的图片中出现的图形是平行四边形,和视频中菱形一致,那么什么是菱形呢?
点击图片,播放视频
实践探究
探究1:菱形的性质
如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
菱形
邻边相等
思考
归纳总结
定义:
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
有一组邻边相等的平行四边形叫做菱形.
(1)菱形是特殊的平行四边形,它具有一般平行四边形的所有性质,你能列举一些这样的性质吗?
(2)你认为菱形还具有哪些特殊的性质?
思考
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
点击图片,播放视频
活动1
在自己剪出的菱形上画出两条折痕,折叠手中的图形(如图),并回答以下问题:
(1)菱形是轴对称图形吗?如果是,它有几条对称轴?对称轴之间有什么位置关系?
(2)菱形中有哪些相等的线段?
活动2
归纳总结
通过上面的折纸活动,我们可以发现菱形是轴对称图形,它有两条对称轴,对称轴互相垂直;它的四条边相等.
探究2
如何推理证明“菱形的四条边相等,对角线互相垂直”这两个性质呢?
A
B
C
O
D
已知:如图,在平行四边形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:(1) AB = BC = CD =AD;
(2) AC⊥BD;
A
B
C
O
D
思考:(1)菱形是特殊的平行四边形,你能从平行四边形的性质证明菱形的四条边相等吗?
(2)可以利用什么性质来证明AC⊥BD.
证明:(1)∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC(平行四边形的对边相等).
又∵AB=AD,
∴AB = BC = CD =AD.
A
B
C
O
D
(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB = OD (菱形的对角线互相平分).
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,
即AC⊥BD.
A
B
C
O
D
归纳
定理 菱形的四条边相等;
定理 菱形的对角线相互垂直.
探究3:定理的拓展延伸
过对“菱形的对角线互相垂直”的证明过程,你还能发现菱形的对角线有什么性质?
方法提示:由折叠过程或等腰三角形“三线合一”推出菱形对角线的性质.
归纳
菱形的每条对角线平分一组对角.
菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
角:对角相等.
边:对边平行且相等.
对角线:相互平分.
菱形的特殊性质
平行四边形的性质
归纳总结
对称性:是轴对称图形.
边:四条边都相等.
对角线:互相垂直,且每条对角线平分一组对角.
应用举例
如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD=6,求菱形的边长AB和对角线AC的长.
例1
解:∵四边形ABCD是菱形,
∴AB=AD(菱形的四条边都相等),AC⊥BD(菱形的对角线互相垂直),
OB=OD= BD= ×6=3(菱形的对角线互相平分).
在等腰△ABD中,∵∠BAD=60°,
∴△ABD是等边三角形,
∴AB=BD=6.
在Rt△AOB中,由勾股定理得OA2+OB2=AB2,
∴OA= ,∴AC=2OA= .
如图,在菱形ABCD中,∠ABC=60°,DE∥AC且交BC的延长线于点E.
求证:DE= BE.
例2
【方法指导】连接BD,由四边形ABCD是菱形,∠ABC=60°,易得BD⊥AC,∠DBC=30°,又由DE∥AC,即可证得DE⊥BD,由30°所对的直角边等于斜边的一半,即可证得DE= BE.
A
B
C
D
E
证明:连接BD.
∵四边形ABCD是菱形,∠ABC=60°,
∴BD⊥AC,∠DBE=30°.
∵DE∥AC,
∴DE⊥BD,即∠BDE=90°.
∵在Rt△BDE中,∠DBE=30°,
∴DE= BE.
A
B
C
D
E
课堂小结
菱形的性质
菱形的性质
有关计算
边
周长=边长的四倍
角
对角线
1.两组对边平行且相等
2.四条边相等
两组对角分别相等,邻角互补邻角互补
1.两条对角线互相垂直平分
2.每一条对角线平分一组对角
随堂练习
知识点1 菱形的定义及对称性
1.下列说法正确的是( )
A.两组对边分别相等的四边形是菱形
B.两组对角分别相等的四边形是菱形
C.一组邻边相等的平行四边形是菱形
D.一组对边平行且相等的四边形是菱形
C
2.如图,在菱形OABC中,若点B在x轴上,点A的坐标为(3,5),则点C的坐标为___________.
(3,-5)
知识点2 菱形的边、角的性质
3.在菱形ABCD 中,若AB=6,则菱形ABCD 的周长为( )
A.6 B.12
C.24 D.48
C
4.如图,已知菱形ABCD.
(1)若∠B=70°,则∠BAC的度数是_______;
(2)若AB=10,∠B=60°,则AC的长为______.
55°
10
5.(教材P9习题T1变式)如图,在菱形ABCD中,点E,F分别在边BC和CD上,且∠AEB=∠AFD.求证:BE=DF.
证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
在△ABE和△ADF中,
∵∠AEB=∠AFD,∠B=∠D,AB=AD,
∴△ABE≌△ADF(AAS),∴BE=DF.
知识点3 菱形的对角线的性质
6.如图,四边形ABCD为菱形,下列描述不一定正确的是( )
A.CA平分∠BCD
B.AC,BD互相平分
C.∠AOB=90°
D.AC=CD
D
7.【新情境·传统文化】中国结寓意团圆、美满,以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴.如图,小陶家有一个中国结装饰,可以近似地看作菱形ABCD,测得BD=16 cm,AC=12 cm,则此菱形的周长为( )
A.28 cm B.40 cm
C.56 cm D.80 cm
B
8.如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )
A. B.1
C. D.
D
[变式](2025·鞍山岫岩月考)如图,在菱形ABCD中,∠A=60°,AD=4,P是边AB上的一个动点,E,F分别是DP,BP的中点,则线段EF的长为( )
A.2 B.4
C.2 D.2
A
9.如图,在平面直角坐标系xOy中,四边形ABCD是菱形,A,B两点的坐标分别是(2,2),(-1,-),点D在第一象限,则点D的坐标是( )
A.(6,2) B.(8,2)
C.(6,) D.(8,)
B
10.(教材P9习题T3变式)如图,四边形ABCD是菱形,CD=5,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6
C. D.12
A
11.如图,在菱形ABCD中,AB的垂直平分线FE交对角线AC于点F,交AB于点E,连接DF.
(1)求证:AF=DF;
解:证明:如图,连接BF.
∵EF垂直平分AB,
∴AF=BF.
∵四边形ABCD是菱形,
∴AD=AB,∠DAF=∠BAF.
又∵AF=AF,
∴△DAF≌△BAF(SAS),
∴DF=BF,
∴AF=DF.
11.如图,在菱形ABCD中,AB的垂直平分线FE交对角线AC于点F,交AB于点E,连接DF.
(2)若∠BAD=70°,求∠FDC的度数.
解:证明:∵四边形ABCD是菱形,∠BAD=70°,
∴∠DAF=∠BAD=35°,
∠ADC=180°-∠BAD=110°.
∵AF=DF,
∴∠ADF=∠DAF=35°,
∴∠FDC=∠ADC-∠ADF=110°-35°=75°.
12.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且点E,F不与点B,C,D重合.
(1)求证:不论点E,F在BC,CD上如何滑动,总有BE=CF.
解:证明:如图,连接AC.
∵四边形ABCD是菱形,∠BAD=120°,
∴∠BAC=∠ACD=∠ABC=∠ACB=60°,
∴∠1+∠EAC=60°,AB=AC.
∵△AEF为等边三角形,
∴∠EAF=∠2+∠EAC=60°,
∴BE=CF.
∴∠1=∠2.
在△ABE和△ACF中,
∵∠1=∠2,AB=AC,∠ABC=∠ACD,
∴△ABE≌△ACF(ASA),
∴BE=CF.
12.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且点E,F不与点B,C,D重合.
(2)点E,F在BC,CD上滑动的过程中,四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.
解:证明:四边形AECF的面积不变,
△CEF的周长发生变化.
由(1),得△ABE≌△ACF,
∴S△ABE=S△ACF,
∴S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值.
过点A作AH⊥BC于点H(图略),则∠AHB=90°.
在Rt△ABH中,∠AHB=90°.
∵∠ABC=60°,∴∠BAH=30°.
∵AB=4,∴BC=4,BH=AB=2,
∴S四边形AECF=S△ABC=BC·AH=BC·
=4.
∵△CEF的周长为CE+CF+EF=CE+BE+
EF=BC+EF=BC+AE,
由“垂线段最短”可知,当等边三角形AEF的边AE与BC垂直时,边AE最短,
∴△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长最小,最小值为4+=4+2.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
