基本算法语句-循环语句
图片预览




文档简介
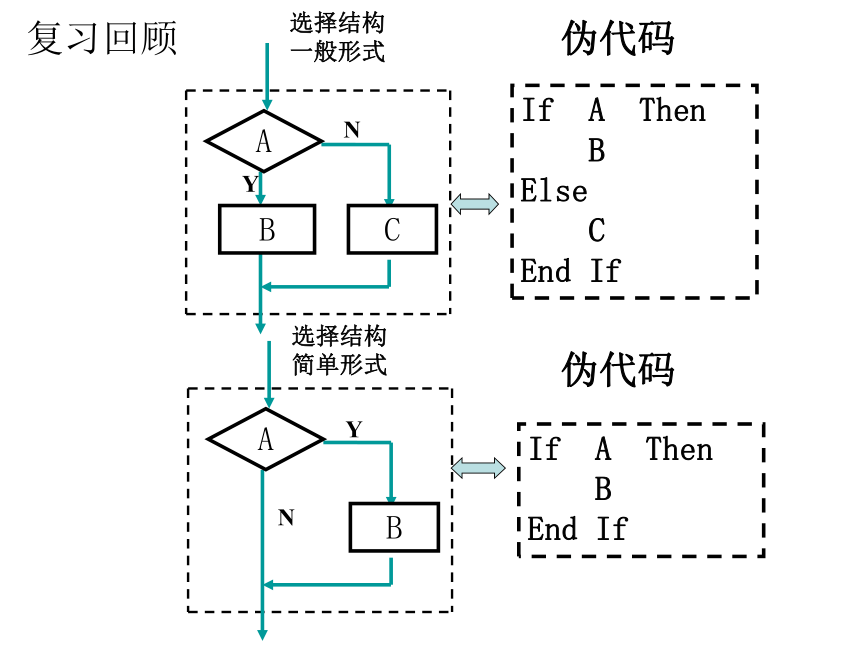
课件18张PPT。循环语句If A Then
B
Else
C
End If伪代码If A Then
B
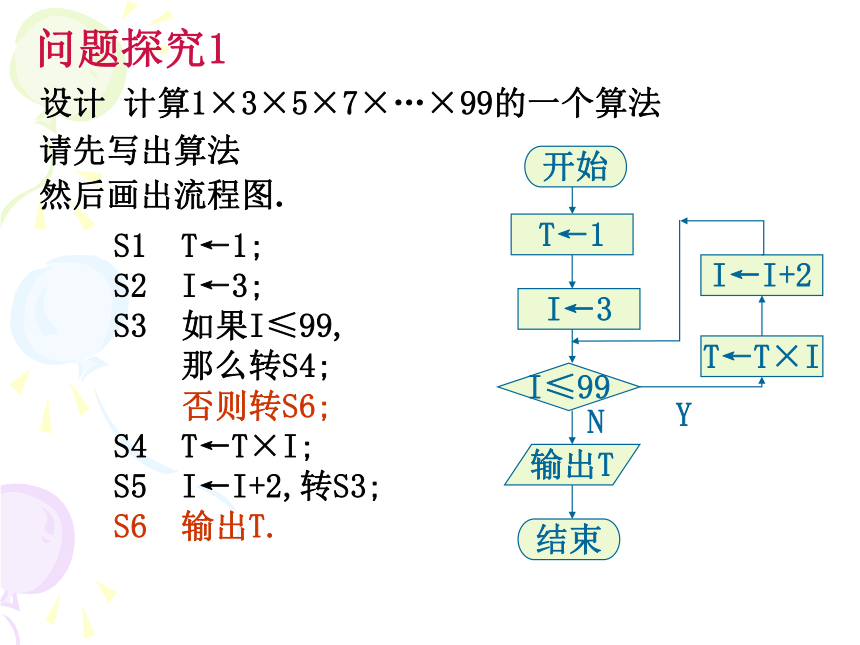
End If伪代码复习回顾问题探究1设计 计算1×3×5×7×…×99的一个算法请先写出算法
然后画出流程图.S1 T←1;
S2 I←3;
S3 如果I≤99,
那么转S4;
否则转S6;
S4 T←T×I;
S5 I←I+2,转S3;
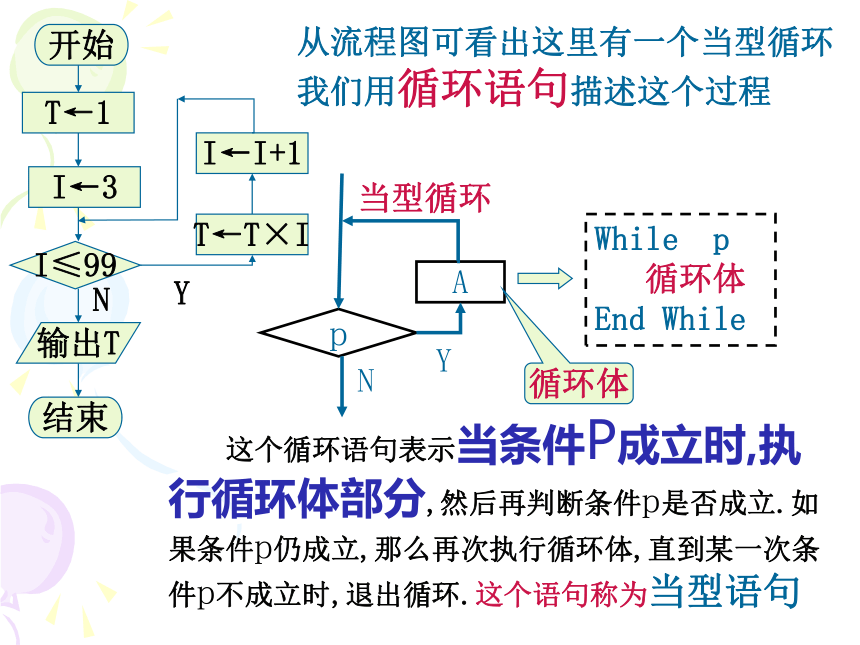
S6 输出T.从流程图可看出这里有一个当型循环我们用循环语句描述这个过程While p
循环体
End While 这个循环语句表示当条件P成立时,执行循环体部分,然后再判断条件p是否成立.如果条件p仍成立,那么再次执行循环体,直到某一次条件p不成立时,退出循环.这个语句称为当型语句循环体S1 T←1;
S2 I←3;
S3 如果I≤99,那么转S4,
否则转S6;
S4 T←T×I;
S5 I←I+2,转S3;
S6 输出T.请用当型语句“While…End While”表示下面算法!T←1
I←3
While I≤99
T←T×I
I←I+2
End While
Print T当型语句特点是:它具有“前测性”,即先判断,后执行。如果条件不成立时,不会执行循环体.任何需要重复处理的问题都可以用这个语句来实现.练习1:下面的程序段的
结果是______.
x←2
i←1
s←0
While i≤4
s←s×x+1
i←i+1
End While
Print s练习2:设计一个计算1×3×5×…×13的算法,下面给出了程序的一部分,则在①上不能填入右面的哪个数.
S←
I←
While I< ①
S←S×I
I←I+2
End Whlie
Print S13
13.5
14
14.13
14.5
14.98练习3 求最小的正整数I,使1×3×5×…×I>10000.请写出算法.
解法1: 用“While”
语句可描述如下:
T←1
I←( ) ?????
While T≤10000
I←I+2
T←T×I
End While
PrintI T←1
I←3 ????
While T≤10000
T←T×I
I←I+2
End While
n←I-2
Print “I=” ; n解法2: 用“While”语句
可描述如下:练习4.2000年我国人口数约为13亿.如果每年的人口自然增长率 为15‰,那么多少年后我国人口将达到或超过15亿?
这个问题可通过循环方式完成计算,即每一次在原有的基础上增加15‰,一直达到或超过15亿,再记下循环次数.试用循环语句表示这一过程.
解:分析:由于循环次数是未知的,因而可以用“While”语句完成.
设人口数为R亿,人口自然增长率为k,经历年数为n,则其伪代码为:R←13
k←0.015
n←0
While R<15
n←n+1
R←R(1+k)
End While
Print n 问题探究2
我们在研究计算1×3×5×7×…×99的算法中,是否可以知道执行循环体的次数呢?
对于循环次数确定与否的问题,都可以用当型语句。
对于循环次数已知的循环我们还可以用“For”语句来描述。“For”语句一般形式为For I From“初值”To“终值”Step“步长”
循环体
End ForS1 T←1;
S2 I←3;
S3 T←T×I
S4 I←I+2
S5 如果I>99,那么转S6
否则转S3;
S6 输出T.T←1
For I From 3 To 99 Step 2
T←T×I
End For
Print T左面的算法用“For”表示为:步长为1时,可以省略“Step“…””For I From“初值”To“终值”Step“步长”
循环体
End For“For”语句一般形式为例题 抛掷一枚硬币时,既可能出现正面,也可能出现反面,预先作出确定的判断是不可能的,但是假如硬币质量均匀,那么当抛掷次数很多时,出现正面的频率应接近于50%.试设计一个循环语句模拟抛掷硬币的过程,并计算抛掷中出现正面的频率.
分析 抛掷硬币的过程实际上是一个不断重复地做同一件事情的过程,利用循环语句,我们容易在计算机上模拟这一过程.
在程序语言中,有一个随机函数“Rnd”,它能产生0到1之间的随机数.这样,我们可用大于0.5的随机数表示出现正面,不大于0.5的随机数表示出现反面.
不妨设抛掷硬币n次,那么我们就可以用“For”语句来完成. s←0 (s表示出现正面的次数)
Read n (n表示掷币的次数)
For i From 1 To n
If Rnd>0.5 Then
s←s+1
End If
End For
p←s/n
Print“正面向上的频率为”;p解法1:算法的伪代码为: s←0 (s表示出现正面的次数)
Read n (n表示掷币的次数)
While i≤n
If Rnd>0.5 Then
s←s+1
End If
End While
p←s/n
Print“正面向上的频率为”;p解法2:用“While”语句描述的伪代码为:S1 T←1;
S2 I←3;
S3 如果I≤99,那么转S4,
否则转S6;
S4 T←T×I;
S5 I←I+2,转S3;
S6 输出T.S1 T←1;
S2 I←3;
S3 T←T×I;
S4 I←I+2;
S5 如果I>99,那么转S6,
否则转S3;
S6 输出T.问题探究3
请把下面的算法改写成直到型循环.直到型循环可用右面的语句来描述!Do
循环体
Until p
End Do这个语句称为直到型语句S1 T←1;
S2 I←3;
S3 T←T×I;
S4 I←I+2;
S5 如果I>99,那么转S6
否则转S3;
S6 输出T.Do
循环体
Until p
End Do上面的算法用直到型语句
“Do…End Do”表示为:T←1
I←3
Do
T←T×I
I←I+2
Until I>99
End Do
Print T直到型语句特点是:
先执行后判断小结:作业P24 4,5,6
B
Else
C
End If伪代码If A Then
B
End If伪代码复习回顾问题探究1设计 计算1×3×5×7×…×99的一个算法请先写出算法
然后画出流程图.S1 T←1;
S2 I←3;
S3 如果I≤99,
那么转S4;
否则转S6;
S4 T←T×I;
S5 I←I+2,转S3;
S6 输出T.从流程图可看出这里有一个当型循环我们用循环语句描述这个过程While p
循环体
End While 这个循环语句表示当条件P成立时,执行循环体部分,然后再判断条件p是否成立.如果条件p仍成立,那么再次执行循环体,直到某一次条件p不成立时,退出循环.这个语句称为当型语句循环体S1 T←1;
S2 I←3;
S3 如果I≤99,那么转S4,
否则转S6;
S4 T←T×I;
S5 I←I+2,转S3;
S6 输出T.请用当型语句“While…End While”表示下面算法!T←1
I←3
While I≤99
T←T×I
I←I+2
End While
Print T当型语句特点是:它具有“前测性”,即先判断,后执行。如果条件不成立时,不会执行循环体.任何需要重复处理的问题都可以用这个语句来实现.练习1:下面的程序段的
结果是______.
x←2
i←1
s←0
While i≤4
s←s×x+1
i←i+1
End While
Print s练习2:设计一个计算1×3×5×…×13的算法,下面给出了程序的一部分,则在①上不能填入右面的哪个数.
S←
I←
While I< ①
S←S×I
I←I+2
End Whlie
Print S13
13.5
14
14.13
14.5
14.98练习3 求最小的正整数I,使1×3×5×…×I>10000.请写出算法.
解法1: 用“While”
语句可描述如下:
T←1
I←( ) ?????
While T≤10000
I←I+2
T←T×I
End While
PrintI T←1
I←3 ????
While T≤10000
T←T×I
I←I+2
End While
n←I-2
Print “I=” ; n解法2: 用“While”语句
可描述如下:练习4.2000年我国人口数约为13亿.如果每年的人口自然增长率 为15‰,那么多少年后我国人口将达到或超过15亿?
这个问题可通过循环方式完成计算,即每一次在原有的基础上增加15‰,一直达到或超过15亿,再记下循环次数.试用循环语句表示这一过程.
解:分析:由于循环次数是未知的,因而可以用“While”语句完成.
设人口数为R亿,人口自然增长率为k,经历年数为n,则其伪代码为:R←13
k←0.015
n←0
While R<15
n←n+1
R←R(1+k)
End While
Print n 问题探究2
我们在研究计算1×3×5×7×…×99的算法中,是否可以知道执行循环体的次数呢?
对于循环次数确定与否的问题,都可以用当型语句。
对于循环次数已知的循环我们还可以用“For”语句来描述。“For”语句一般形式为For I From“初值”To“终值”Step“步长”
循环体
End ForS1 T←1;
S2 I←3;
S3 T←T×I
S4 I←I+2
S5 如果I>99,那么转S6
否则转S3;
S6 输出T.T←1
For I From 3 To 99 Step 2
T←T×I
End For
Print T左面的算法用“For”表示为:步长为1时,可以省略“Step“…””For I From“初值”To“终值”Step“步长”
循环体
End For“For”语句一般形式为例题 抛掷一枚硬币时,既可能出现正面,也可能出现反面,预先作出确定的判断是不可能的,但是假如硬币质量均匀,那么当抛掷次数很多时,出现正面的频率应接近于50%.试设计一个循环语句模拟抛掷硬币的过程,并计算抛掷中出现正面的频率.
分析 抛掷硬币的过程实际上是一个不断重复地做同一件事情的过程,利用循环语句,我们容易在计算机上模拟这一过程.
在程序语言中,有一个随机函数“Rnd”,它能产生0到1之间的随机数.这样,我们可用大于0.5的随机数表示出现正面,不大于0.5的随机数表示出现反面.
不妨设抛掷硬币n次,那么我们就可以用“For”语句来完成. s←0 (s表示出现正面的次数)
Read n (n表示掷币的次数)
For i From 1 To n
If Rnd>0.5 Then
s←s+1
End If
End For
p←s/n
Print“正面向上的频率为”;p解法1:算法的伪代码为: s←0 (s表示出现正面的次数)
Read n (n表示掷币的次数)
While i≤n
If Rnd>0.5 Then
s←s+1
End If
End While
p←s/n
Print“正面向上的频率为”;p解法2:用“While”语句描述的伪代码为:S1 T←1;
S2 I←3;
S3 如果I≤99,那么转S4,
否则转S6;
S4 T←T×I;
S5 I←I+2,转S3;
S6 输出T.S1 T←1;
S2 I←3;
S3 T←T×I;
S4 I←I+2;
S5 如果I>99,那么转S6,
否则转S3;
S6 输出T.问题探究3
请把下面的算法改写成直到型循环.直到型循环可用右面的语句来描述!Do
循环体
Until p
End Do这个语句称为直到型语句S1 T←1;
S2 I←3;
S3 T←T×I;
S4 I←I+2;
S5 如果I>99,那么转S6
否则转S3;
S6 输出T.Do
循环体
Until p
End Do上面的算法用直到型语句
“Do…End Do”表示为:T←1
I←3
Do
T←T×I
I←I+2
Until I>99
End Do
Print T直到型语句特点是:
先执行后判断小结:作业P24 4,5,6
