2026年高三数学上学期专题突破练:空间向量与立体几何(含解析)
文档属性
| 名称 | 2026年高三数学上学期专题突破练:空间向量与立体几何(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-11 11:28:48 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2026年高三数学上学期专题突破练:空间向量与立体几何
一.选择题(共8小题)
1.(2025春 江苏月考)若平面α的一个法向量为且该平面过点A(6,3,0),则点P(5,1,5)到平面α的距离为( )
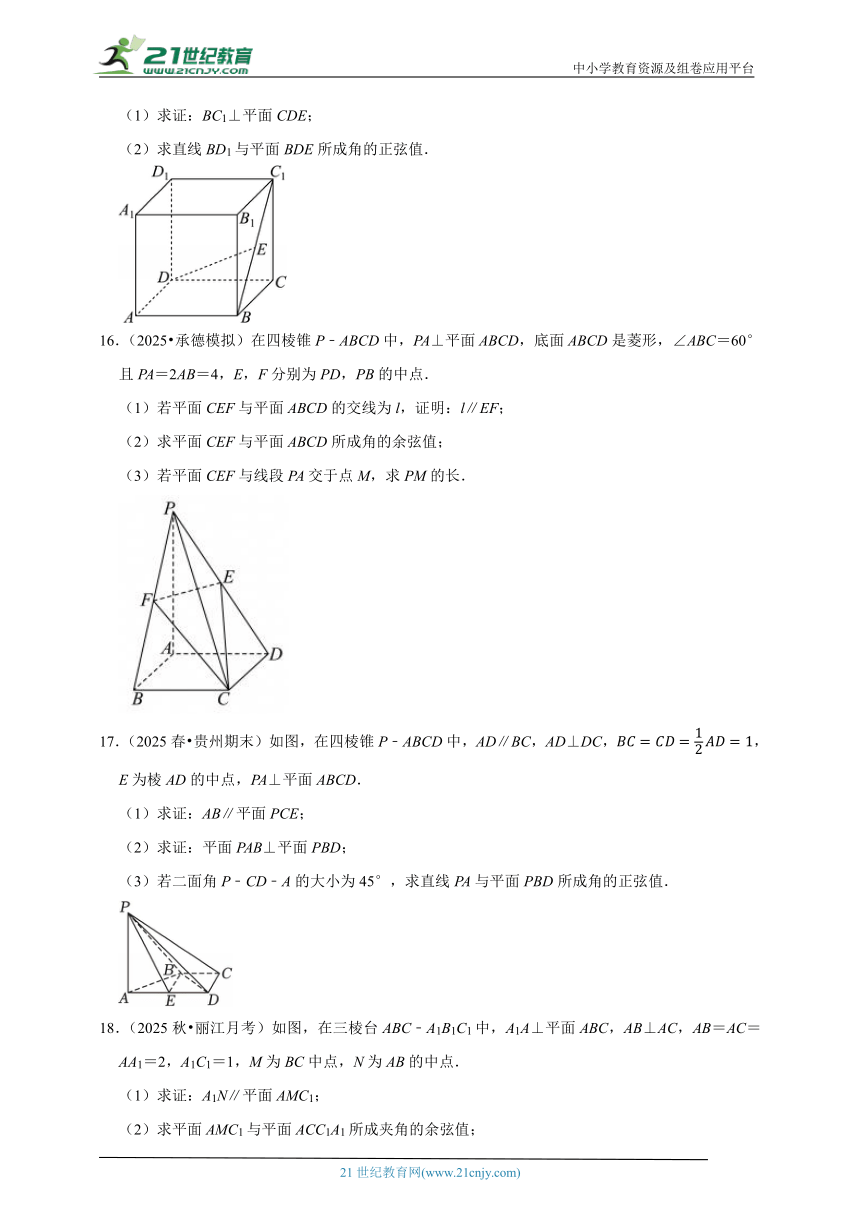
A. B. C. D.
2.(2025春 庐山市 月考)在三棱锥P﹣ABC中,P(0,0,1),,,C(2,0,0),则PC与平面PAB所成角的正弦值为( )
A. B. C. D.
3.(2025春 民勤县校级期中)若向量,,且与的夹角余弦值为,则λ等于( )
A. B. C. D.
4.(2025春 环县校级期中)点A(3,4,5)关于坐标平面Oyz对称的点B的坐标为( )
A.(3,4,﹣5) B.(﹣3,4,5)
C.(﹣3,4,﹣5) D.(﹣3,﹣4,﹣5)
5.(2025春 龙潭区校级期末)某公司利用无人机进行餐点即时的送,利用空间坐标表示无人机的位置,开始时无人机在点O(0,0,0)处起飞,6秒后到达点A(0,0,90)处,15秒后到达点B处,若,则( )
A. B.120 C.150 D.210
6.(2025春 安徽月考)设空间两个单位向量与向量的夹角等于,则向量夹角的余弦值等于( )
A. B. C. D.
7.(2025春 南充月考)如图,正方体ABCD﹣A1B1C1D1中,P为BC的中点,点Q为四边形CC1D1D及其内部的动点,PQ∥平面BB1D1D.则PQ与平面ABCD所成角正切值的范围( )
A. B. C. D.
8.(2025春 环县校级期中)如图所示,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为平行四边形,BD⊥DC,BD=DC=1,点E在AA1上,且,则点B到平面EDC1的距离为( )
A. B. C. D.
二.多选题(共3小题)
(多选)9.(2025春 民勤县校级期中)如图,已知平行六面体ABCD﹣A′B′C′D′,点E是CC′的中点,下列结论中正确的是( )
A. B.
C. D.
(多选)10.(2025 锦江区校级模拟)已知正方体ABCD﹣A1B1C1D1的棱长为,点M在底面ABCD上(含边界),且,则下列说法正确的是( )
A.点M的轨迹的长度为
B.直线BM与平面CDD1C1所成角的正切值最大为
C.平面AB1C截该正方体的内切球所得截面的面积为
D.若动点N在线段BD1上,P为B1D1的中点,则MN+NP的最小值为
(多选)11.(2025 吉林模拟)如图,在正方体ABCD﹣A1B1C1D1中,E,F分别是AB,B1C的中点,G是棱A1D1上的动点,则下列说法正确的有( )
A.EF⊥平面A1BD
B.存在点G,满足C1G∥平面B1EF
C.当且仅当D1G=3GA1时,GE+GF取得最小值
D.直线BD1与平面CDG所成角的正弦值的最大值为
三.填空题(共3小题)
12.(2025春 宝山区校级期中)已知空间向量,,若的夹角为钝角,则实数λ的取值范围为 .
13.(2025春 龙潭区校级期末)已知平面α的法向量为,点A(0,1,1)为平面α内一点,点P(1,0,2)为平面α外一点,则点P到平面α的距离为 .
14.(2025春 江北区校级期中)如图所示,已知在三棱锥A﹣BCD中,二面角A﹣BD﹣C为直二面角,BC⊥CD,CB=CD=2,AB=AD=2,若三棱锥A﹣BCD的各个顶点都在同一个球面上,则该球的体积为 .
四.解答题(共5小题)
15.(2025春 兰州校级期中)如图,正方体ABCD﹣A1B1C1D1的棱长为2,E是BC1的中点.
(1)求证:BC1⊥平面CDE;
(2)求直线BD1与平面BDE所成角的正弦值.
16.(2025 承德模拟)在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,∠ABC=60°且PA=2AB=4,E,F分别为PD,PB的中点.
(1)若平面CEF与平面ABCD的交线为l,证明:l∥EF;
(2)求平面CEF与平面ABCD所成角的余弦值;
(3)若平面CEF与线段PA交于点M,求PM的长.
17.(2025春 贵州期末)如图,在四棱锥P﹣ABCD中,AD∥BC,AD⊥DC,,E为棱AD的中点,PA⊥平面ABCD.
(1)求证:AB∥平面PCE;
(2)求证:平面PAB⊥平面PBD;
(3)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PBD所成角的正弦值.
18.(2025秋 丽江月考)如图,在三棱台ABC﹣A1B1C1中,A1A⊥平面ABC,AB⊥AC,AB=AC=AA1=2,A1C1=1,M为BC中点,N为AB的中点.
(1)求证:A1N∥平面AMC1;
(2)求平面AMC1与平面ACC1A1所成夹角的余弦值;
(3)求点C到平面AMC1的距离.
19.(2025 西青区校级三模)如图,在四棱锥P﹣ABCD中.底面ABCD为矩形,侧棱PD⊥底面ABCD,PD=DC=2AD=2,E是PC的中点.
(1)求证:PA∥平面EDB;
(2)求平面EDB与平面PAD夹角的余弦值;
(3)若,且点F到平面EDB的距离为,求λ的值.
2026年高三数学上学期专题突破练:空间向量与立体几何
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C A B C D D C
二.多选题(共3小题)
题号 9 10 11
答案 ACD ACD ACD
一.选择题(共8小题)
1.(2025春 江苏月考)若平面α的一个法向量为且该平面过点A(6,3,0),则点P(5,1,5)到平面α的距离为( )
A. B. C. D.
【解答】解:因为点A(6,3,0),点P(5,1,5),
所以,
又平面α的一个法向量为,
所以点P(5,1,5)到平面α的距离为.
故选:B.
2.(2025春 庐山市 月考)在三棱锥P﹣ABC中,P(0,0,1),,,C(2,0,0),则PC与平面PAB所成角的正弦值为( )
A. B. C. D.
【解答】解:因为P(0,0,1),,,C(2,0,0),
故,
设平面PAB的一个法向量,
则,则,
令y=1,则,
故,
设PC与平面PAB所成角为θ,
则.
故选:C.
3.(2025春 民勤县校级期中)若向量,,且与的夹角余弦值为,则λ等于( )
A. B. C. D.
【解答】解:∵向量,,且与的夹角余弦值为,
∴cos,,
解得,
由已知得λ<0,∴.
故选:A.
4.(2025春 环县校级期中)点A(3,4,5)关于坐标平面Oyz对称的点B的坐标为( )
A.(3,4,﹣5) B.(﹣3,4,5)
C.(﹣3,4,﹣5) D.(﹣3,﹣4,﹣5)
【解答】解:关于坐标平面Oyz对称的点,横坐标变换为其相反数,纵坐标、竖坐标不变.
即点A(3,4,5)关于坐标平面Oyz对称的点B的坐标为(﹣3,4,5).
故选:B.
5.(2025春 龙潭区校级期末)某公司利用无人机进行餐点即时的送,利用空间坐标表示无人机的位置,开始时无人机在点O(0,0,0)处起飞,6秒后到达点A(0,0,90)处,15秒后到达点B处,若,则( )
A. B.120 C.150 D.210
【解答】解:由题意可知,,
所以.
故选:C.
6.(2025春 安徽月考)设空间两个单位向量与向量的夹角等于,则向量夹角的余弦值等于( )
A. B. C. D.
【解答】解:由题意得p+n,||1,||,
∴p+n=1,
∵p2+n2=1,∴np,
则向量夹角的余弦值为:
cos,np.
故选:D.
7.(2025春 南充月考)如图,正方体ABCD﹣A1B1C1D1中,P为BC的中点,点Q为四边形CC1D1D及其内部的动点,PQ∥平面BB1D1D.则PQ与平面ABCD所成角正切值的范围( )
A. B. C. D.
【解答】解:在正方体ABCD﹣A1B1C1D1中,取线段CD,C1D1,B1C1的中点分别为E,F,G,
连接EF,EP,FG,GP,
因为EF∥PG,
所以四点E,F,G,P四点共面,
又因为BB1∥PG,BB1 平面BB1D1D,PG 平面BB1D1D,
所以PG∥平面BB1D1D,
又因为D1B1∥FG,D1B1 平面BB1D1D,FG 平面BB1D1D,
所以FG∥平面BB1D1D,
又因为FG∩PG=G,FG,PG 平面EFGP,
所以平面EFGP∥平面BB1D1D,
因为点Q为四边形CC1D1D及其内部的动点,所以当Q∈EF,即PQ 平面EFGP,
所以此时有PQ∥平面BB1D1D,
因为QE⊥平面ABCD,
所以PQ与平面ABCD所成角就是∠QPE,
又因为,
设正方体的棱长为2,则,
此时QE∈[0,2],所以.
故选:D.
8.(2025春 环县校级期中)如图所示,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为平行四边形,BD⊥DC,BD=DC=1,点E在AA1上,且,则点B到平面EDC1的距离为( )
A. B. C. D.
【解答】解:建立如图所示的空间直角坐标系,
则,
所以,
设平面EDC1的法向量为,
则,
所以,
所以点B到平面EDC1的距离.
故选:C.
二.多选题(共3小题)
(多选)9.(2025春 民勤县校级期中)如图,已知平行六面体ABCD﹣A′B′C′D′,点E是CC′的中点,下列结论中正确的是( )
A. B.
C. D.
【解答】解:底面ABCD是平行四边形可知:,所以A正确;
,所以B不正确;
,所以C正确;
,所以D正确.
故选:ACD.
(多选)10.(2025 锦江区校级模拟)已知正方体ABCD﹣A1B1C1D1的棱长为,点M在底面ABCD上(含边界),且,则下列说法正确的是( )
A.点M的轨迹的长度为
B.直线BM与平面CDD1C1所成角的正切值最大为
C.平面AB1C截该正方体的内切球所得截面的面积为
D.若动点N在线段BD1上,P为B1D1的中点,则MN+NP的最小值为
【解答】解:对于选项A,根据正方体性质可得,可知DM=1,
故点M的轨迹是以D为圆心,1为半径的四分之一圆,如下图所示:
则其轨迹的长度为,故选项A正确;
对于选项B,易知当点M位于棱CD上时,直线BM与平面CDD1C1所成的角最大,
此时,
即直线BM与平面CDD1C1所成角的正切值最大为,故选项B错误;
对于选项C,易知内切球的半径为,球心O位于正方体的中心,其到平面AB1C的距离为d,
易知,,点B平面AB1C的距离为;
可得球心O到平面AB1C的距离为,
故截面圆的半径r满足,则所得截面的面积为,故选项C正确;
对于选项D,如下图:
先固定点N,当点M在BD上时,MN最小,
再让点N移动,当P,N,M三点共线时,MN+NP最小,
此时,故选项D正确.
故选:ACD.
(多选)11.(2025 吉林模拟)如图,在正方体ABCD﹣A1B1C1D1中,E,F分别是AB,B1C的中点,G是棱A1D1上的动点,则下列说法正确的有( )
A.EF⊥平面A1BD
B.存在点G,满足C1G∥平面B1EF
C.当且仅当D1G=3GA1时,GE+GF取得最小值
D.直线BD1与平面CDG所成角的正弦值的最大值为
【解答】解:如图,以点D为原点建立空间直角坐标系,
设正方体的棱长为2,D1G=a(0≤a≤2),
则A(2,0,0),B(2,2,0),C(0,2,0),D(0,0,0),A1(2,0,2),B1(2,2,2),C1(0,2,2),
D1(0,0,2),E(2,1,0),F(1,2,1),G(a,0,2),
对于A,,
则,
所以EF⊥DA1,EF⊥DB,
又DA1∩DB=D,DA1,DB 平面A1BD,
所以EF⊥平面A1BD,故A正确;
对于B,,
设平面B1EF的法向量为,
则,则有,
取y=2,则,
若C1G∥平面B1EF,则,
解得a=4,
又因为0≤a≤4,
所以不存在点G,满足C1G∥平面B1EF,故B错误;
对于C,,
则,
可看作点M(a,0)到点N(2,5)与到点T(1,5)的距离之和,
点N(2,5)关于x轴的对称点N′(2,﹣5),
则当M,T,N′三点共线时,点M(a,0)到点N′(2,﹣5)与到点T(1,5)的距离之和最小,
即点M(a,0)到点N(2,5)与到点T(1,5)的距离之和最小,
,
因为,
所以﹣10(1﹣a)﹣5=0,解得,
所以当时,GE+GF取得最小值,
此时,即D1G=3GA1,故C正确;
对于D,,
设平面CDG的法向量为,
则,则有,
取x2=2,则,
设直线BD1与平面CDG所成的角为α,
则,
令t=a+2,t∈[2,4],则a=t﹣2,
则,
当,即t=4,即a=2时,sinα取得最大值,最大值为,故D正确.
故选:ACD.
三.填空题(共3小题)
12.(2025春 宝山区校级期中)已知空间向量,,若的夹角为钝角,则实数λ的取值范围为 (0,2)∪(2,+∞) .
【解答】解:由,,
且的夹角为钝角,
可得且与不反向共线,
由,可得﹣2+2﹣λ2+λ(λ﹣6)<0,
整理得﹣6λ<0,解得λ>0,
当与共线时,设,
则有,解得,
当λ=2时,有,不合题意,
故实数λ的取值范围是(0,2)∪(2,+∞).
故答案为:(0,2)∪(2,+∞).
13.(2025春 龙潭区校级期末)已知平面α的法向量为,点A(0,1,1)为平面α内一点,点P(1,0,2)为平面α外一点,则点P到平面α的距离为 1 .
【解答】解:由题意得,
又平面α的法向量为,
∴点P到平面α的距离.
故答案为:1.
14.(2025春 江北区校级期中)如图所示,已知在三棱锥A﹣BCD中,二面角A﹣BD﹣C为直二面角,BC⊥CD,CB=CD=2,AB=AD=2,若三棱锥A﹣BCD的各个顶点都在同一个球面上,则该球的体积为 .
【解答】解:在三棱锥A﹣BCD中,取BD的中点E,连接AE,
因为AB=AD,所以AE⊥BD,
因为二面角A﹣BD﹣C为直二面角,因为AE 平面ABD,
所以AE⊥平面BCD,
因为BC⊥CD,,所以,,
,
所以,
AC=AB=AD,
因为BC⊥CD,所以外接球的球心在AE上,设为O,连接BO、DO,
则BO2=BE2+OE2=BE2+(AE﹣AO)2,
可得,
解得,
所以该球的体积为.
故答案为:.
四.解答题(共5小题)
15.(2025春 兰州校级期中)如图,正方体ABCD﹣A1B1C1D1的棱长为2,E是BC1的中点.
(1)求证:BC1⊥平面CDE;
(2)求直线BD1与平面BDE所成角的正弦值.
【解答】解:(1)证明:连接CE,在正方体ABCD﹣A1B1C1D1中,
因为DC⊥平面BCC1B1,又BC1 平面BCC1B1,
所以DC⊥BC1,又因为四边形BCC1B1是正方形,E是BC1的中点,
所以CE⊥BC1,又CE∩CD=C,CE,CD 平面CDE,
所以BC1⊥平面CDE;
(2)以D为坐标原点,分别以DA,DC,DD1所在直线分别为x,y,z轴建立空间直角坐标系,由棱长为2,
则D(0,0,0),B(2,2,0),C1(02,2),D1(0,0,2),E(1,2,1),
所以,
设平面BDE的法向量为,
则,所以,
令x=1得,
设直线BD1与平面BDE所成角为θ,
所以,
所以直线BD1与平面BDE所成角的正弦值为.
16.(2025 承德模拟)在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,∠ABC=60°且PA=2AB=4,E,F分别为PD,PB的中点.
(1)若平面CEF与平面ABCD的交线为l,证明:l∥EF;
(2)求平面CEF与平面ABCD所成角的余弦值;
(3)若平面CEF与线段PA交于点M,求PM的长.
【解答】解:(1)证明:如图所示,连接BD,因为E,F分别是PD,PB的中点,
所以EF∥BD,
EF 平面ABCD,BD 平面ABCD,那么EF∥平面ABCD,
又EF 平面CEF,平面CEF∩平面ABCD=l,
所以l∥EF;
(2)因为底面ABCD为菱形,∠ABC=60°,设CD中点为G,易知AB,AG,AP两两互相垂直,
故以点A为坐标原点,直线AB,AG,AP分别为x,y,z轴建立如图所示的空间直角坐标系,
由题意PA=2AB=4,所以,P(0,0,4),B(2,0,0),F(1,0,2),,,
显然平面ABCD的法向量可以是,
而,,
设平面CEF的法向量为,
则,则,
令,解得y=2,,
所以可取,
故
所以平面CEF与平面ABCD所成角的余弦值为;
(3)设M(0,0,a),则C,E,M,F四点共面.,
由(2)知平面CEF的法向量为,
则,即,
解得,所以.
17.(2025春 贵州期末)如图,在四棱锥P﹣ABCD中,AD∥BC,AD⊥DC,,E为棱AD的中点,PA⊥平面ABCD.
(1)求证:AB∥平面PCE;
(2)求证:平面PAB⊥平面PBD;
(3)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PBD所成角的正弦值.
【解答】(1)证明:连接CE,
因为AD∥BC,,且E是AD的中点,
所以AE∥BC,AE=BC,
所以四边形ABCE是平行四边形,
所以AB∥CE,
又AB 平面PCE,CE 平面PCE,
所以AB∥平面PCE.
(2)证明:在直角梯形ABCD中,,
所以AB,BD,
所以AB2+BD2=AD2,即AB⊥BD,
因为PA⊥平面ABCD,BD 平面ABCD,
所以PA⊥BD,
又AB∩PA=A,AB、PA 平面PAB,
所以BD⊥平面PAB,
又BD 平面PBD,
所以平面PAB⊥平面PBD.
(3)解:因为PA⊥平面ABCD,AD⊥DC,
所以由三垂线定理知,PD⊥CD,
所以∠ADP就是二面角P﹣CD﹣A的平面角,即∠ADP=45°,
所以PA=AD=2,
所以PB,
由(2)知,平面PAB⊥平面PBD,
所以直线PA与平面PBD所成角即为∠APB,
在Rt△PAB中,sin∠APB,
故直线PA与平面PBD所成角的正弦值为.
18.(2025秋 丽江月考)如图,在三棱台ABC﹣A1B1C1中,A1A⊥平面ABC,AB⊥AC,AB=AC=AA1=2,A1C1=1,M为BC中点,N为AB的中点.
(1)求证:A1N∥平面AMC1;
(2)求平面AMC1与平面ACC1A1所成夹角的余弦值;
(3)求点C到平面AMC1的距离.
【解答】解:(1)证明:连接MN,C1A,由M,N分别是BC,BA的中点,
根据中位线性质,MN∥AC,且,
由棱台性质,A1C1∥AC,于是MN∥A1C1,
由MN=A1C1=1可知,四边形MNA1C1是平行四边形,则A1N∥MC1,
又A1N 平面C1MA,MC1 平面C1MA,
于是A1N∥平面AMC1;
(2)过M作ME⊥AC,垂足为E,过E作EF⊥AC1,垂足为F,连接MF,C1E,
由ME 平面ABC,A1A⊥平面ABC,
故AA1⊥ME,
又ME⊥AC,AC∩AA1=A,AC,AA1 平面ACC1A1,
则ME⊥平面ACC1A1,
由AC1 平面ACC1A1,故ME⊥AC1,
又EF⊥AC1,ME∩EF=E,ME,EF 平面MEF,
于是AC1⊥平面MEF,
由MF 平面MEF,故AC1⊥MF,
于是平面AMC1与平面ACC1A1所成角即为∠MFE,
又,,
则,故,
在Rt△MEF中,∠MEF=90°,则,
于是;
(3)过C1作C1P⊥AC,垂足为P,作C1Q⊥AM,垂足为Q,
连接PQ,PM,过P作PR⊥C1Q,垂足为R,
由题干数据可得,,,
根据勾股定理,,
由C1P⊥平面AMC,AM 平面AMC,则C1P⊥AM,
又C1Q⊥AM,C1Q∩C1P=C1,C1Q,C1P 平面C1PQ,
于是AM⊥平面C1PQ,
又PR 平面C1PQ,则PR⊥AM,
又PR⊥C1Q,C1Q∩AM=Q,C1Q,AM 平面C1MA,
故PR⊥平面C1MA,
在Rt△C1PQ中,,
又CA=2PA,故点C到平面C1MA的距离是P到平面C1MA的距离的两倍,
即点C到平面AMC1的距离是,
19.(2025 西青区校级三模)如图,在四棱锥P﹣ABCD中.底面ABCD为矩形,侧棱PD⊥底面ABCD,PD=DC=2AD=2,E是PC的中点.
(1)求证:PA∥平面EDB;
(2)求平面EDB与平面PAD夹角的余弦值;
(3)若,且点F到平面EDB的距离为,求λ的值.
【解答】解:(1)证明:如图,连结AC,交BD于点O,连结OE,
因为点E是PC的中点,底面ABCD为矩形,
所以点O是AC的中点,
所以PA∥OE,
因为OE 平面EDB,PA 平面EDB,
所以PA∥平面EDB;
(2)如图,以向量为x,y,z轴的正方向建立空间直角坐标系,
D(0,0,0),B(1,2,0),P(0,0,2),C(0,2,0),E(0,1,1),
则,,
设平面EDB的法向量,
则,则,令y=﹣1,x=2,z=1,
所以平面EDB的法向量,
且平面PAD的一个法向量为,
设平面EDB和平面PAD的夹角为θ,
则,
所以平面EDB和平面PAD的夹角的余弦值为.
(3)由(2)可得D(0,0,0),B(1,2,0),E(0,1,1),P(0,0,2),
,,
平面EDB的法向量,
故,
设点F与平面EDB的距离为d,
则,
解得.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年高三数学上学期专题突破练:空间向量与立体几何
一.选择题(共8小题)
1.(2025春 江苏月考)若平面α的一个法向量为且该平面过点A(6,3,0),则点P(5,1,5)到平面α的距离为( )
A. B. C. D.
2.(2025春 庐山市 月考)在三棱锥P﹣ABC中,P(0,0,1),,,C(2,0,0),则PC与平面PAB所成角的正弦值为( )
A. B. C. D.
3.(2025春 民勤县校级期中)若向量,,且与的夹角余弦值为,则λ等于( )
A. B. C. D.
4.(2025春 环县校级期中)点A(3,4,5)关于坐标平面Oyz对称的点B的坐标为( )
A.(3,4,﹣5) B.(﹣3,4,5)
C.(﹣3,4,﹣5) D.(﹣3,﹣4,﹣5)
5.(2025春 龙潭区校级期末)某公司利用无人机进行餐点即时的送,利用空间坐标表示无人机的位置,开始时无人机在点O(0,0,0)处起飞,6秒后到达点A(0,0,90)处,15秒后到达点B处,若,则( )
A. B.120 C.150 D.210
6.(2025春 安徽月考)设空间两个单位向量与向量的夹角等于,则向量夹角的余弦值等于( )
A. B. C. D.
7.(2025春 南充月考)如图,正方体ABCD﹣A1B1C1D1中,P为BC的中点,点Q为四边形CC1D1D及其内部的动点,PQ∥平面BB1D1D.则PQ与平面ABCD所成角正切值的范围( )
A. B. C. D.
8.(2025春 环县校级期中)如图所示,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为平行四边形,BD⊥DC,BD=DC=1,点E在AA1上,且,则点B到平面EDC1的距离为( )
A. B. C. D.
二.多选题(共3小题)
(多选)9.(2025春 民勤县校级期中)如图,已知平行六面体ABCD﹣A′B′C′D′,点E是CC′的中点,下列结论中正确的是( )
A. B.
C. D.
(多选)10.(2025 锦江区校级模拟)已知正方体ABCD﹣A1B1C1D1的棱长为,点M在底面ABCD上(含边界),且,则下列说法正确的是( )
A.点M的轨迹的长度为
B.直线BM与平面CDD1C1所成角的正切值最大为
C.平面AB1C截该正方体的内切球所得截面的面积为
D.若动点N在线段BD1上,P为B1D1的中点,则MN+NP的最小值为
(多选)11.(2025 吉林模拟)如图,在正方体ABCD﹣A1B1C1D1中,E,F分别是AB,B1C的中点,G是棱A1D1上的动点,则下列说法正确的有( )
A.EF⊥平面A1BD
B.存在点G,满足C1G∥平面B1EF
C.当且仅当D1G=3GA1时,GE+GF取得最小值
D.直线BD1与平面CDG所成角的正弦值的最大值为
三.填空题(共3小题)
12.(2025春 宝山区校级期中)已知空间向量,,若的夹角为钝角,则实数λ的取值范围为 .
13.(2025春 龙潭区校级期末)已知平面α的法向量为,点A(0,1,1)为平面α内一点,点P(1,0,2)为平面α外一点,则点P到平面α的距离为 .
14.(2025春 江北区校级期中)如图所示,已知在三棱锥A﹣BCD中,二面角A﹣BD﹣C为直二面角,BC⊥CD,CB=CD=2,AB=AD=2,若三棱锥A﹣BCD的各个顶点都在同一个球面上,则该球的体积为 .
四.解答题(共5小题)
15.(2025春 兰州校级期中)如图,正方体ABCD﹣A1B1C1D1的棱长为2,E是BC1的中点.
(1)求证:BC1⊥平面CDE;
(2)求直线BD1与平面BDE所成角的正弦值.
16.(2025 承德模拟)在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,∠ABC=60°且PA=2AB=4,E,F分别为PD,PB的中点.
(1)若平面CEF与平面ABCD的交线为l,证明:l∥EF;
(2)求平面CEF与平面ABCD所成角的余弦值;
(3)若平面CEF与线段PA交于点M,求PM的长.
17.(2025春 贵州期末)如图,在四棱锥P﹣ABCD中,AD∥BC,AD⊥DC,,E为棱AD的中点,PA⊥平面ABCD.
(1)求证:AB∥平面PCE;
(2)求证:平面PAB⊥平面PBD;
(3)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PBD所成角的正弦值.
18.(2025秋 丽江月考)如图,在三棱台ABC﹣A1B1C1中,A1A⊥平面ABC,AB⊥AC,AB=AC=AA1=2,A1C1=1,M为BC中点,N为AB的中点.
(1)求证:A1N∥平面AMC1;
(2)求平面AMC1与平面ACC1A1所成夹角的余弦值;
(3)求点C到平面AMC1的距离.
19.(2025 西青区校级三模)如图,在四棱锥P﹣ABCD中.底面ABCD为矩形,侧棱PD⊥底面ABCD,PD=DC=2AD=2,E是PC的中点.
(1)求证:PA∥平面EDB;
(2)求平面EDB与平面PAD夹角的余弦值;
(3)若,且点F到平面EDB的距离为,求λ的值.
2026年高三数学上学期专题突破练:空间向量与立体几何
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C A B C D D C
二.多选题(共3小题)
题号 9 10 11
答案 ACD ACD ACD
一.选择题(共8小题)
1.(2025春 江苏月考)若平面α的一个法向量为且该平面过点A(6,3,0),则点P(5,1,5)到平面α的距离为( )
A. B. C. D.
【解答】解:因为点A(6,3,0),点P(5,1,5),
所以,
又平面α的一个法向量为,
所以点P(5,1,5)到平面α的距离为.
故选:B.
2.(2025春 庐山市 月考)在三棱锥P﹣ABC中,P(0,0,1),,,C(2,0,0),则PC与平面PAB所成角的正弦值为( )
A. B. C. D.
【解答】解:因为P(0,0,1),,,C(2,0,0),
故,
设平面PAB的一个法向量,
则,则,
令y=1,则,
故,
设PC与平面PAB所成角为θ,
则.
故选:C.
3.(2025春 民勤县校级期中)若向量,,且与的夹角余弦值为,则λ等于( )
A. B. C. D.
【解答】解:∵向量,,且与的夹角余弦值为,
∴cos,,
解得,
由已知得λ<0,∴.
故选:A.
4.(2025春 环县校级期中)点A(3,4,5)关于坐标平面Oyz对称的点B的坐标为( )
A.(3,4,﹣5) B.(﹣3,4,5)
C.(﹣3,4,﹣5) D.(﹣3,﹣4,﹣5)
【解答】解:关于坐标平面Oyz对称的点,横坐标变换为其相反数,纵坐标、竖坐标不变.
即点A(3,4,5)关于坐标平面Oyz对称的点B的坐标为(﹣3,4,5).
故选:B.
5.(2025春 龙潭区校级期末)某公司利用无人机进行餐点即时的送,利用空间坐标表示无人机的位置,开始时无人机在点O(0,0,0)处起飞,6秒后到达点A(0,0,90)处,15秒后到达点B处,若,则( )
A. B.120 C.150 D.210
【解答】解:由题意可知,,
所以.
故选:C.
6.(2025春 安徽月考)设空间两个单位向量与向量的夹角等于,则向量夹角的余弦值等于( )
A. B. C. D.
【解答】解:由题意得p+n,||1,||,
∴p+n=1,
∵p2+n2=1,∴np,
则向量夹角的余弦值为:
cos,np.
故选:D.
7.(2025春 南充月考)如图,正方体ABCD﹣A1B1C1D1中,P为BC的中点,点Q为四边形CC1D1D及其内部的动点,PQ∥平面BB1D1D.则PQ与平面ABCD所成角正切值的范围( )
A. B. C. D.
【解答】解:在正方体ABCD﹣A1B1C1D1中,取线段CD,C1D1,B1C1的中点分别为E,F,G,
连接EF,EP,FG,GP,
因为EF∥PG,
所以四点E,F,G,P四点共面,
又因为BB1∥PG,BB1 平面BB1D1D,PG 平面BB1D1D,
所以PG∥平面BB1D1D,
又因为D1B1∥FG,D1B1 平面BB1D1D,FG 平面BB1D1D,
所以FG∥平面BB1D1D,
又因为FG∩PG=G,FG,PG 平面EFGP,
所以平面EFGP∥平面BB1D1D,
因为点Q为四边形CC1D1D及其内部的动点,所以当Q∈EF,即PQ 平面EFGP,
所以此时有PQ∥平面BB1D1D,
因为QE⊥平面ABCD,
所以PQ与平面ABCD所成角就是∠QPE,
又因为,
设正方体的棱长为2,则,
此时QE∈[0,2],所以.
故选:D.
8.(2025春 环县校级期中)如图所示,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为平行四边形,BD⊥DC,BD=DC=1,点E在AA1上,且,则点B到平面EDC1的距离为( )
A. B. C. D.
【解答】解:建立如图所示的空间直角坐标系,
则,
所以,
设平面EDC1的法向量为,
则,
所以,
所以点B到平面EDC1的距离.
故选:C.
二.多选题(共3小题)
(多选)9.(2025春 民勤县校级期中)如图,已知平行六面体ABCD﹣A′B′C′D′,点E是CC′的中点,下列结论中正确的是( )
A. B.
C. D.
【解答】解:底面ABCD是平行四边形可知:,所以A正确;
,所以B不正确;
,所以C正确;
,所以D正确.
故选:ACD.
(多选)10.(2025 锦江区校级模拟)已知正方体ABCD﹣A1B1C1D1的棱长为,点M在底面ABCD上(含边界),且,则下列说法正确的是( )
A.点M的轨迹的长度为
B.直线BM与平面CDD1C1所成角的正切值最大为
C.平面AB1C截该正方体的内切球所得截面的面积为
D.若动点N在线段BD1上,P为B1D1的中点,则MN+NP的最小值为
【解答】解:对于选项A,根据正方体性质可得,可知DM=1,
故点M的轨迹是以D为圆心,1为半径的四分之一圆,如下图所示:
则其轨迹的长度为,故选项A正确;
对于选项B,易知当点M位于棱CD上时,直线BM与平面CDD1C1所成的角最大,
此时,
即直线BM与平面CDD1C1所成角的正切值最大为,故选项B错误;
对于选项C,易知内切球的半径为,球心O位于正方体的中心,其到平面AB1C的距离为d,
易知,,点B平面AB1C的距离为;
可得球心O到平面AB1C的距离为,
故截面圆的半径r满足,则所得截面的面积为,故选项C正确;
对于选项D,如下图:
先固定点N,当点M在BD上时,MN最小,
再让点N移动,当P,N,M三点共线时,MN+NP最小,
此时,故选项D正确.
故选:ACD.
(多选)11.(2025 吉林模拟)如图,在正方体ABCD﹣A1B1C1D1中,E,F分别是AB,B1C的中点,G是棱A1D1上的动点,则下列说法正确的有( )
A.EF⊥平面A1BD
B.存在点G,满足C1G∥平面B1EF
C.当且仅当D1G=3GA1时,GE+GF取得最小值
D.直线BD1与平面CDG所成角的正弦值的最大值为
【解答】解:如图,以点D为原点建立空间直角坐标系,
设正方体的棱长为2,D1G=a(0≤a≤2),
则A(2,0,0),B(2,2,0),C(0,2,0),D(0,0,0),A1(2,0,2),B1(2,2,2),C1(0,2,2),
D1(0,0,2),E(2,1,0),F(1,2,1),G(a,0,2),
对于A,,
则,
所以EF⊥DA1,EF⊥DB,
又DA1∩DB=D,DA1,DB 平面A1BD,
所以EF⊥平面A1BD,故A正确;
对于B,,
设平面B1EF的法向量为,
则,则有,
取y=2,则,
若C1G∥平面B1EF,则,
解得a=4,
又因为0≤a≤4,
所以不存在点G,满足C1G∥平面B1EF,故B错误;
对于C,,
则,
可看作点M(a,0)到点N(2,5)与到点T(1,5)的距离之和,
点N(2,5)关于x轴的对称点N′(2,﹣5),
则当M,T,N′三点共线时,点M(a,0)到点N′(2,﹣5)与到点T(1,5)的距离之和最小,
即点M(a,0)到点N(2,5)与到点T(1,5)的距离之和最小,
,
因为,
所以﹣10(1﹣a)﹣5=0,解得,
所以当时,GE+GF取得最小值,
此时,即D1G=3GA1,故C正确;
对于D,,
设平面CDG的法向量为,
则,则有,
取x2=2,则,
设直线BD1与平面CDG所成的角为α,
则,
令t=a+2,t∈[2,4],则a=t﹣2,
则,
当,即t=4,即a=2时,sinα取得最大值,最大值为,故D正确.
故选:ACD.
三.填空题(共3小题)
12.(2025春 宝山区校级期中)已知空间向量,,若的夹角为钝角,则实数λ的取值范围为 (0,2)∪(2,+∞) .
【解答】解:由,,
且的夹角为钝角,
可得且与不反向共线,
由,可得﹣2+2﹣λ2+λ(λ﹣6)<0,
整理得﹣6λ<0,解得λ>0,
当与共线时,设,
则有,解得,
当λ=2时,有,不合题意,
故实数λ的取值范围是(0,2)∪(2,+∞).
故答案为:(0,2)∪(2,+∞).
13.(2025春 龙潭区校级期末)已知平面α的法向量为,点A(0,1,1)为平面α内一点,点P(1,0,2)为平面α外一点,则点P到平面α的距离为 1 .
【解答】解:由题意得,
又平面α的法向量为,
∴点P到平面α的距离.
故答案为:1.
14.(2025春 江北区校级期中)如图所示,已知在三棱锥A﹣BCD中,二面角A﹣BD﹣C为直二面角,BC⊥CD,CB=CD=2,AB=AD=2,若三棱锥A﹣BCD的各个顶点都在同一个球面上,则该球的体积为 .
【解答】解:在三棱锥A﹣BCD中,取BD的中点E,连接AE,
因为AB=AD,所以AE⊥BD,
因为二面角A﹣BD﹣C为直二面角,因为AE 平面ABD,
所以AE⊥平面BCD,
因为BC⊥CD,,所以,,
,
所以,
AC=AB=AD,
因为BC⊥CD,所以外接球的球心在AE上,设为O,连接BO、DO,
则BO2=BE2+OE2=BE2+(AE﹣AO)2,
可得,
解得,
所以该球的体积为.
故答案为:.
四.解答题(共5小题)
15.(2025春 兰州校级期中)如图,正方体ABCD﹣A1B1C1D1的棱长为2,E是BC1的中点.
(1)求证:BC1⊥平面CDE;
(2)求直线BD1与平面BDE所成角的正弦值.
【解答】解:(1)证明:连接CE,在正方体ABCD﹣A1B1C1D1中,
因为DC⊥平面BCC1B1,又BC1 平面BCC1B1,
所以DC⊥BC1,又因为四边形BCC1B1是正方形,E是BC1的中点,
所以CE⊥BC1,又CE∩CD=C,CE,CD 平面CDE,
所以BC1⊥平面CDE;
(2)以D为坐标原点,分别以DA,DC,DD1所在直线分别为x,y,z轴建立空间直角坐标系,由棱长为2,
则D(0,0,0),B(2,2,0),C1(02,2),D1(0,0,2),E(1,2,1),
所以,
设平面BDE的法向量为,
则,所以,
令x=1得,
设直线BD1与平面BDE所成角为θ,
所以,
所以直线BD1与平面BDE所成角的正弦值为.
16.(2025 承德模拟)在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,∠ABC=60°且PA=2AB=4,E,F分别为PD,PB的中点.
(1)若平面CEF与平面ABCD的交线为l,证明:l∥EF;
(2)求平面CEF与平面ABCD所成角的余弦值;
(3)若平面CEF与线段PA交于点M,求PM的长.
【解答】解:(1)证明:如图所示,连接BD,因为E,F分别是PD,PB的中点,
所以EF∥BD,
EF 平面ABCD,BD 平面ABCD,那么EF∥平面ABCD,
又EF 平面CEF,平面CEF∩平面ABCD=l,
所以l∥EF;
(2)因为底面ABCD为菱形,∠ABC=60°,设CD中点为G,易知AB,AG,AP两两互相垂直,
故以点A为坐标原点,直线AB,AG,AP分别为x,y,z轴建立如图所示的空间直角坐标系,
由题意PA=2AB=4,所以,P(0,0,4),B(2,0,0),F(1,0,2),,,
显然平面ABCD的法向量可以是,
而,,
设平面CEF的法向量为,
则,则,
令,解得y=2,,
所以可取,
故
所以平面CEF与平面ABCD所成角的余弦值为;
(3)设M(0,0,a),则C,E,M,F四点共面.,
由(2)知平面CEF的法向量为,
则,即,
解得,所以.
17.(2025春 贵州期末)如图,在四棱锥P﹣ABCD中,AD∥BC,AD⊥DC,,E为棱AD的中点,PA⊥平面ABCD.
(1)求证:AB∥平面PCE;
(2)求证:平面PAB⊥平面PBD;
(3)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PBD所成角的正弦值.
【解答】(1)证明:连接CE,
因为AD∥BC,,且E是AD的中点,
所以AE∥BC,AE=BC,
所以四边形ABCE是平行四边形,
所以AB∥CE,
又AB 平面PCE,CE 平面PCE,
所以AB∥平面PCE.
(2)证明:在直角梯形ABCD中,,
所以AB,BD,
所以AB2+BD2=AD2,即AB⊥BD,
因为PA⊥平面ABCD,BD 平面ABCD,
所以PA⊥BD,
又AB∩PA=A,AB、PA 平面PAB,
所以BD⊥平面PAB,
又BD 平面PBD,
所以平面PAB⊥平面PBD.
(3)解:因为PA⊥平面ABCD,AD⊥DC,
所以由三垂线定理知,PD⊥CD,
所以∠ADP就是二面角P﹣CD﹣A的平面角,即∠ADP=45°,
所以PA=AD=2,
所以PB,
由(2)知,平面PAB⊥平面PBD,
所以直线PA与平面PBD所成角即为∠APB,
在Rt△PAB中,sin∠APB,
故直线PA与平面PBD所成角的正弦值为.
18.(2025秋 丽江月考)如图,在三棱台ABC﹣A1B1C1中,A1A⊥平面ABC,AB⊥AC,AB=AC=AA1=2,A1C1=1,M为BC中点,N为AB的中点.
(1)求证:A1N∥平面AMC1;
(2)求平面AMC1与平面ACC1A1所成夹角的余弦值;
(3)求点C到平面AMC1的距离.
【解答】解:(1)证明:连接MN,C1A,由M,N分别是BC,BA的中点,
根据中位线性质,MN∥AC,且,
由棱台性质,A1C1∥AC,于是MN∥A1C1,
由MN=A1C1=1可知,四边形MNA1C1是平行四边形,则A1N∥MC1,
又A1N 平面C1MA,MC1 平面C1MA,
于是A1N∥平面AMC1;
(2)过M作ME⊥AC,垂足为E,过E作EF⊥AC1,垂足为F,连接MF,C1E,
由ME 平面ABC,A1A⊥平面ABC,
故AA1⊥ME,
又ME⊥AC,AC∩AA1=A,AC,AA1 平面ACC1A1,
则ME⊥平面ACC1A1,
由AC1 平面ACC1A1,故ME⊥AC1,
又EF⊥AC1,ME∩EF=E,ME,EF 平面MEF,
于是AC1⊥平面MEF,
由MF 平面MEF,故AC1⊥MF,
于是平面AMC1与平面ACC1A1所成角即为∠MFE,
又,,
则,故,
在Rt△MEF中,∠MEF=90°,则,
于是;
(3)过C1作C1P⊥AC,垂足为P,作C1Q⊥AM,垂足为Q,
连接PQ,PM,过P作PR⊥C1Q,垂足为R,
由题干数据可得,,,
根据勾股定理,,
由C1P⊥平面AMC,AM 平面AMC,则C1P⊥AM,
又C1Q⊥AM,C1Q∩C1P=C1,C1Q,C1P 平面C1PQ,
于是AM⊥平面C1PQ,
又PR 平面C1PQ,则PR⊥AM,
又PR⊥C1Q,C1Q∩AM=Q,C1Q,AM 平面C1MA,
故PR⊥平面C1MA,
在Rt△C1PQ中,,
又CA=2PA,故点C到平面C1MA的距离是P到平面C1MA的距离的两倍,
即点C到平面AMC1的距离是,
19.(2025 西青区校级三模)如图,在四棱锥P﹣ABCD中.底面ABCD为矩形,侧棱PD⊥底面ABCD,PD=DC=2AD=2,E是PC的中点.
(1)求证:PA∥平面EDB;
(2)求平面EDB与平面PAD夹角的余弦值;
(3)若,且点F到平面EDB的距离为,求λ的值.
【解答】解:(1)证明:如图,连结AC,交BD于点O,连结OE,
因为点E是PC的中点,底面ABCD为矩形,
所以点O是AC的中点,
所以PA∥OE,
因为OE 平面EDB,PA 平面EDB,
所以PA∥平面EDB;
(2)如图,以向量为x,y,z轴的正方向建立空间直角坐标系,
D(0,0,0),B(1,2,0),P(0,0,2),C(0,2,0),E(0,1,1),
则,,
设平面EDB的法向量,
则,则,令y=﹣1,x=2,z=1,
所以平面EDB的法向量,
且平面PAD的一个法向量为,
设平面EDB和平面PAD的夹角为θ,
则,
所以平面EDB和平面PAD的夹角的余弦值为.
(3)由(2)可得D(0,0,0),B(1,2,0),E(0,1,1),P(0,0,2),
,,
平面EDB的法向量,
故,
设点F与平面EDB的距离为d,
则,
解得.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
