2026年高三数学上学期专题突破练:立体几何初步(含解析)
文档属性
| 名称 | 2026年高三数学上学期专题突破练:立体几何初步(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-11 11:31:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2026年高三数学上学期专题突破练:立体几何初步
一.选择题(共8小题)
1.(2025春 浙江期中)下列说法正确的是( )
A.有两个面互相平行,其余各面都是平行四边形的几何体一定是棱柱
B.如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥可能为六棱锥
C.棱台的各侧棱延长后必交于一点
D.以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台
2.(2025春 长春期中)已知直角梯形ABCD中,AB⊥AD,AB∥CD,AB=6,CD=4,,则直角梯形ABCD的直观图A′B′C′D′的面积为( )
A.5 B. C.10 D.
3.(2025春 长安区校级期中)已知m,n表示不同的直线,α,β表示不同的平面,A表示点,则下列命题正确的是( )
A.若直线m上有无数个点在平面α内,则m∥α
B.若m α,n β,且α∥β,则m∥n
C.若m α,n β,则m∥n
D.若α∩β=m,且A∈α,A∈β,则A∈m
4.(2025秋 丽江月考)已知圆锥的轴截面为正三角形,且圆锥的体积为,若该圆锥的底面圆周和顶点都在同一球面上,则该球的表面积为( )
A. B.2π C.6π D.
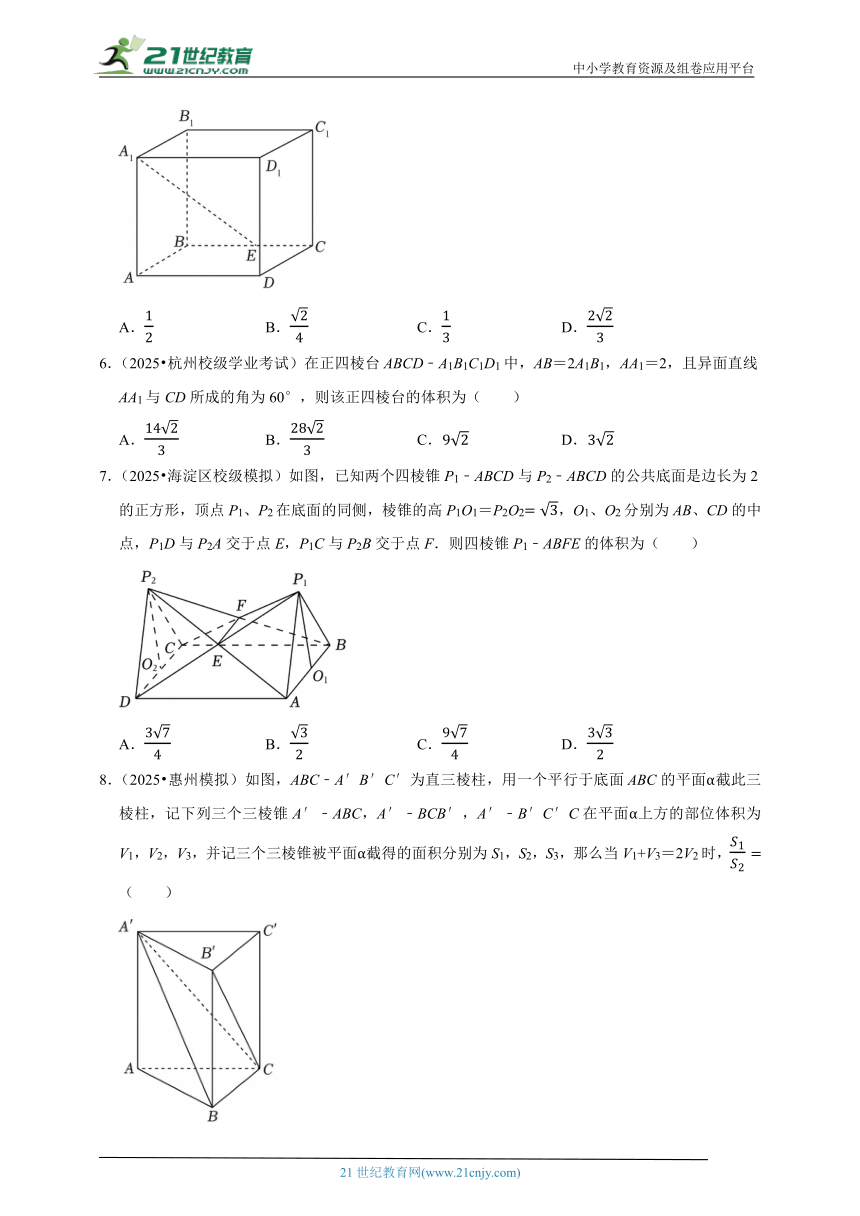
5.(2025春 安徽月考)如图,已知在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2,AD=3,点E在棱BC上,且,则直线A1E与直线C1D1所成角的余弦值为( )
A. B. C. D.
6.(2025 杭州校级学业考试)在正四棱台ABCD﹣A1B1C1D1中,AB=2A1B1,AA1=2,且异面直线AA1与CD所成的角为60°,则该正四棱台的体积为( )
A. B. C. D.
7.(2025 海淀区校级模拟)如图,已知两个四棱锥P1﹣ABCD与P2﹣ABCD的公共底面是边长为2的正方形,顶点P1、P2在底面的同侧,棱锥的高P1O1=P2O2,O1、O2分别为AB、CD的中点,P1D与P2A交于点E,P1C与P2B交于点F.则四棱锥P1﹣ABFE的体积为( )
A. B. C. D.
8.(2025 惠州模拟)如图,ABC﹣A′B′C′为直三棱柱,用一个平行于底面ABC的平面α截此三棱柱,记下列三个三棱锥A′﹣ABC,A′﹣BCB′,A′﹣B′C′C在平面α上方的部位体积为V1,V2,V3,并记三个三棱锥被平面α截得的面积分别为S1,S2,S3,那么当V1+V3=2V2时,( )
A. B. C.1 D.
二.多选题(共3小题)
(多选)9.(2025春 长春期中)已知圆锥SO的母线长为4,其侧面积是底面积的2倍,则( )
A.该圆锥的表面积为12π
B.该圆锥的体积为
C.该圆锥侧面展开图为半圆
D.该圆锥轴截面为等边三角形
(多选)10.(2025春 重庆校级期中)已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
A.若m∥n,n α,m α,则m∥α
B.若m∥α,α∥β,则m∥β
C.若m∥α,n∥α,则m∥n
D.若α∥β,m α,则m∥β
(多选)11.(2025春 长春期中)半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体体现了数学的对称美.按照以下方式可构造一个半正多面体:如图,在一个棱长为4的正方体中,B1E1=B1F1=B1G1=a,A1E2=A1F2=A1G2=a,…,a∈(0,4),过E1,F1,G1三点可做一截面,类似地,可做8个形状完全相同的截面.关于该几何体,下列说法正确的是( )
A.当a=1时,该几何体是一个半正多面体
B.当a=3时,该几何体是一个半正多面体
C.若该几何体是由正八边形与正三角形围成的半正多面体,则边长为
D.若该几何体是由正方形与正三角形围成的半正多面体,则体积为32
三.填空题(共3小题)
12.(2025 枣庄校级二模)在三棱锥D﹣ABC中,△ABC是边长为的等边三角形,侧面DAB⊥底面ABC,∠ADB=120°.若三棱锥D﹣ABC的四个顶点均在同一球面上,则该球的表面积为 ,三棱锥D﹣ABC体积的最大值为 .
13.(2025春 丹东期末)已知等边△ABC的边长为,AD是BC边上的高,以AD为折痕将△ACD折起,使∠BDC=60°,则三棱锥A﹣BCD外接球的表面积为 .
14.(2025春 天津期中)阿基米德(Archimedes,公元前287年﹣公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为36π,则圆柱的表面积为 .
四.解答题(共5小题)
15.(2025春 长乐区校级期中)已知正方体ABCD﹣A1B1C1D1的棱长为2,P为AC的中点.
(1)证明:D1P∥平面A1BC1;
(2)求三棱锥B1﹣A1BC1的体积.
16.(2025春 城东区校级期中)如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥DC,AD⊥DC,DA=AB=2,DC=4,E,F分别为棱CD,PD的中点.
(1)求证:PB∥平面AEF;
(2)求证:AE⊥平面PBD.
(3)求证:平面AEF∥平面PBC.
17.(2025春 云南月考)在如图所示的几何体中,直线PD⊥底面ABCD,MA∥PD,底面ABCD是正方形,E,F,G分别为MB,PC,PB的中点,AD=PD=2.
(1)求证:PB⊥AC;
(2)求证:平面EFG∥平面ADPM;
(3)求直线PB与平面EFG所成角的正弦值.
18.(2025春 长春期中)如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点O为AC与BD的交点,点P为DD1的中点.
(1)求证:直线BD1∥平面PAC;
(2)求三棱锥B﹣PAC的体积.
19.(2025春 江北区校级期中)已知四棱锥P﹣ABCD的底面ABCD为是边长为1的正方形,PC⊥平面ABCD
(1)求证:BD⊥平面PAC;
(2)若PC=BC,平面PAB与平面PCD的交线为l,求直线l与直线PA所成角的余弦值;
(3)若E为PB中点,且直线DE与平面ABE所成角的正弦值为,求PC.
2026年高三数学上学期专题突破练:立体几何初步
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C A D D C B B B
二.多选题(共3小题)
题号 9 10 11
答案 ACD AD BC
一.选择题(共8小题)
1.(2025春 浙江期中)下列说法正确的是( )
A.有两个面互相平行,其余各面都是平行四边形的几何体一定是棱柱
B.如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥可能为六棱锥
C.棱台的各侧棱延长后必交于一点
D.以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台
【解答】解:根据题意,依次分析选项:
对于A,有两个面互相平行,其余各面都是平行四边形的几何体,若侧棱不平行,则不为棱柱,故A错误;
对于B,棱锥的各个侧面都是等边三角形,则顶角为60°,
若为六棱锥,则60°×6=360°,为一个周角,故为平面图形,故B错误;
对于C,由棱台的定义,棱台的各侧棱延长后必交于一点,C正确;
对于D,以直角梯形的一腰所在直线为轴旋转,如果旋转轴是梯形的斜边,则旋转体不是圆台,D错误.
故选:C.
2.(2025春 长春期中)已知直角梯形ABCD中,AB⊥AD,AB∥CD,AB=6,CD=4,,则直角梯形ABCD的直观图A′B′C′D′的面积为( )
A.5 B. C.10 D.
【解答】解:因为直角梯形ABCD中,AB⊥AD,AB∥CD,AB=6,CD=4,,
所以SABCD(6+4)10,
故直角梯形ABCD的直观图A′B′C′D′的面积为:SABCD105.
故选:A.
3.(2025春 长安区校级期中)已知m,n表示不同的直线,α,β表示不同的平面,A表示点,则下列命题正确的是( )
A.若直线m上有无数个点在平面α内,则m∥α
B.若m α,n β,且α∥β,则m∥n
C.若m α,n β,则m∥n
D.若α∩β=m,且A∈α,A∈β,则A∈m
【解答】解:已知m,n表示不同的直线,α,β表示不同的平面,A表示点,
对于A,若直线m上有无数个点在平面α内,
则m α,
即A错误;
对于B,若m α,n β,且α∥β,
则m∥n或m与n异面,
即B错误;
对于C,若m α,n β,
则m与n的位置关系不确定,
即C错误;
对于D,若α∩β=m,且A∈α,A∈β,
则A∈m,
即D正确.
故选:D.
4.(2025秋 丽江月考)已知圆锥的轴截面为正三角形,且圆锥的体积为,若该圆锥的底面圆周和顶点都在同一球面上,则该球的表面积为( )
A. B.2π C.6π D.
【解答】解:因为圆锥的轴截面为正三角形,且圆锥的体积为,
所以作出示意图如下:
设圆锥的底面半径为r,则圆锥的母线l=2r,高.
所以圆锥的体积为,解得,则,
设球的半径为R,球心到圆锥底面的距离为d,
则,即,解得,
所以球的表面积为.
故选:D.
5.(2025春 安徽月考)如图,已知在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2,AD=3,点E在棱BC上,且,则直线A1E与直线C1D1所成角的余弦值为( )
A. B. C. D.
【解答】解:以D为原点,分别以DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系,如图,
∴AA1=2AB=2,AD=3,则AB=1,AA1=2,
∴A1(3,0,2),C1(0,1,2),D1(0,0,2).
∵点E在棱BC上,且,BC=AD=3,
∴BE=2,EC=1,则E(1,1,0).
∴,
.
∴cos,
∵异面直线所成角的范围是,
∴直线A1E与直线C1D1所成角的余弦值为.
故选:C.
6.(2025 杭州校级学业考试)在正四棱台ABCD﹣A1B1C1D1中,AB=2A1B1,AA1=2,且异面直线AA1与CD所成的角为60°,则该正四棱台的体积为( )
A. B. C. D.
【解答】解:作出示意图如下:
∵AB∥CD,
∴异面直线AA1与CD所成的角为∠A1AB=60°,
过A1作A1M⊥AC于M,过M作MN⊥AB于N,
则A1M⊥AB,A1M⊥NM,
又A1M∩MN=M,
∴AB⊥平面A1MN,∴A1N⊥AB,
∵AB=2A1B1,AA1=2,∴,AN=AA1cos60°=1,
∴2A1B1=A1B1+2,∴A1B1=2,∴AB=4,
∵△ANM∽△ABC,∴,∴MN=1,∴,
∴该正四棱台的体积为:
.
故选:B.
7.(2025 海淀区校级模拟)如图,已知两个四棱锥P1﹣ABCD与P2﹣ABCD的公共底面是边长为2的正方形,顶点P1、P2在底面的同侧,棱锥的高P1O1=P2O2,O1、O2分别为AB、CD的中点,P1D与P2A交于点E,P1C与P2B交于点F.则四棱锥P1﹣ABFE的体积为( )
A. B. C. D.
【解答】解:连接P1P2,O1O2,O1D,如图所示.
因为P1O1平面ABCD,P2O2⊥平面ABCD,所以P1O1∥P2O2,
又P1O1=P2O2,所以四边形P1O1O2P2是矩形,所以P1P2∥O1O2,且P1P2=O1O2,
又O1,O2分别为AB,CD的中点,所以O1O2∥AD且O1O2=AD,
所以P1P2∥AD且P1P2=AD,所以四边形P1P2DA为平行四边形,
又对角线P2A∩DP1=E,所以E为P1D的中点.
连接P2O1,交EF于点N,过点P作P1M⊥P2O1于M,由题意知P2A=P2B,故P2O1⊥AB,
又P1O1⊥AB,P2O1∩P1O1=O1,P2O1,P1O1 平面P2P1O1,所以AB⊥平面P2P1O1.
因为P1M 平面P2P1O1,故AB⊥P1M.
又P2O1∩AB=O1,P2O1,AB 平面P2AB,所以P1M⊥平面P2AB,即P1M是四棱锥P1﹣ABFE的高,
同理可得点F为线段P1C的中点,所以EF∥CD,且,
在Rt△P2O2O1中,,则,
所以,
因为,
所以.
故选:B.
8.(2025 惠州模拟)如图,ABC﹣A′B′C′为直三棱柱,用一个平行于底面ABC的平面α截此三棱柱,记下列三个三棱锥A′﹣ABC,A′﹣BCB′,A′﹣B′C′C在平面α上方的部位体积为V1,V2,V3,并记三个三棱锥被平面α截得的面积分别为S1,S2,S3,那么当V1+V3=2V2时,( )
A. B. C.1 D.
【解答】解:如图所示,设直三棱柱的底面积为S,体积为V,
如图所示,,所以,
此时.
此时平面α在直棱柱的中间高度上,
故平面α与A′B,A′C,B′C相交于它们的中点处,此时截面如图所示:
可知,.
故选:B.
二.多选题(共3小题)
(多选)9.(2025春 长春期中)已知圆锥SO的母线长为4,其侧面积是底面积的2倍,则( )
A.该圆锥的表面积为12π
B.该圆锥的体积为
C.该圆锥侧面展开图为半圆
D.该圆锥轴截面为等边三角形
【解答】解:圆锥SO的母线长为4,其侧面积是底面积的2倍,
设圆锥底面半径为r,
则底面面积S1=πr2,底面周长C=2πr,
故侧面面积S2cl=4πr,
由题意得S2=2S1,即4πr=2πr2,即r=2,
故侧面面积S2cl=4πr=8π,可得表面积为:8π+4π=12π,A选项正确;
侧面面积S2=8ππ 42,所以该圆锥侧面展开图为半圆,C选项正确;
设该圆锥母线与底面所成角为α,则cosα,即α=60°,故圆锥轴截面为等边三角形,D选项正确;
则该圆锥的体积VS1hS1lsinα4π×4π,B选项不正确.
故选:ACD.
(多选)10.(2025春 重庆校级期中)已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
A.若m∥n,n α,m α,则m∥α
B.若m∥α,α∥β,则m∥β
C.若m∥α,n∥α,则m∥n
D.若α∥β,m α,则m∥β
【解答】解:若m∥n,n α,m α,则m∥α,所以A选项正确;
若m∥α,α∥β,则m∥β或m β,所以B选项错误;
若m∥α,n∥α,则m∥n或m与n相交或异面,所以C选项错误;
若α∥β,m α,则m∥β,所以D选项正确.
故选:AD.
(多选)11.(2025春 长春期中)半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体体现了数学的对称美.按照以下方式可构造一个半正多面体:如图,在一个棱长为4的正方体中,B1E1=B1F1=B1G1=a,A1E2=A1F2=A1G2=a,…,a∈(0,4),过E1,F1,G1三点可做一截面,类似地,可做8个形状完全相同的截面.关于该几何体,下列说法正确的是( )
A.当a=1时,该几何体是一个半正多面体
B.当a=3时,该几何体是一个半正多面体
C.若该几何体是由正八边形与正三角形围成的半正多面体,则边长为
D.若该几何体是由正方形与正三角形围成的半正多面体,则体积为32
【解答】解:对A选项,当a=1时,8个顶角的截面为等边三角形,但其余保留的每个面不是正八边形,所以A选项错误;
对B选项,当a=3时,8个顶角的截面为正六边形,其余保留的每个面是正方形,所以B选项正确;
对C选项,如图,因为棱长为4的正方体中,B1E1=B1F1=B1G1=a,A1E2=A1F2=A1G2=a,…,a∈(0,4),
所以,E1F2=4﹣2a,
当此半正多面体是由正八边形与正三角形围成时,,(,解得,故C正确;
对于D,当此半正多面体是由正方形与正三角形围成时,E1F2=4﹣2a=0,
所以a=2,表面积为,D错误.
故选:BC.
三.填空题(共3小题)
12.(2025 枣庄校级二模)在三棱锥D﹣ABC中,△ABC是边长为的等边三角形,侧面DAB⊥底面ABC,∠ADB=120°.若三棱锥D﹣ABC的四个顶点均在同一球面上,则该球的表面积为 5π ,三棱锥D﹣ABC体积的最大值为 .
【解答】解:如图①,设△ABC,△DAB的外接圆的圆心分别为O1,O2,半径为r1,r2,三棱锥D﹣ABC的外接球的球心为O,半径为R,
设AB的中点为E,则,即r1=1,同理可得r2=1.
因为侧面DAB⊥底面ABC,EO2⊥AB,可得EO2⊥底面ABC,所以EO2⊥EO1.
又OO1⊥底面ABC,OO2⊥侧面DAB,所以四边形OO1EO2为矩形.
在Rt△OO2A中,,
因为,所以,所以球O的表面积为5π.
设三棱锥D﹣ABC的高为h,过D作DH⊥AB于点H,
由面面垂直的性质可得,DH⊥底面ABC,即DH为三棱锥D﹣ABC的高.
△DAB及其外接圆如图②所示,由图可知,当D位于劣弧AB的中点时,h最大,最大值为,
所以三棱锥D﹣ABC体积的最大值为.
故答案为:5π;.
13.(2025春 丹东期末)已知等边△ABC的边长为,AD是BC边上的高,以AD为折痕将△ACD折起,使∠BDC=60°,则三棱锥A﹣BCD外接球的表面积为 52π .
【解答】解:根据题意作出示意图,如下图所示:
易知AD⊥DB,AD⊥DC,又BD∩DC=B,BD,DC 平面BDC,
所以AD⊥平面BDC,
设△BDC外接圆圆心为O1,过O1做面BDC垂线,
则垂线上所有点到△BDC顶点距离相等,且垂线与AD共面,
过A做上述垂线的垂线,垂足为O2,所以得四边形AO2O1D为矩形,
取O1O2中点为O,易知O为三棱锥A﹣BCD外接球球心,
所以AD=O1O2=6 OO1=3,
根据正弦定理有,
则OD满足,
所以外接球的表面积为.
故答案为:52π.
14.(2025春 天津期中)阿基米德(Archimedes,公元前287年﹣公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为36π,则圆柱的表面积为 54π .
【解答】解:设球的半径为r,则圆柱的底面半径也为r,高为2r,
所以球的体积公为,所以r=3,
所以圆柱的表面积为πr2×2+2πr 2r=6πr2=6π×9=54π.
故答案为:54π.
四.解答题(共5小题)
15.(2025春 长乐区校级期中)已知正方体ABCD﹣A1B1C1D1的棱长为2,P为AC的中点.
(1)证明:D1P∥平面A1BC1;
(2)求三棱锥B1﹣A1BC1的体积.
【解答】解:(1)证明:如图,设B1D1∩A1C1=H,连接BH,
因为DD1∥BB1,DD1=BB1,
所以四边形B1BDD1为平行四边形,
所以BD∥B1D1,
又P为AC的中点,H为B1D1的中点,
所以D1H∥BP,且D1H=BP,
所以四边形D1HBP是平行四边形,
所以BH∥D1P,又D1P 平面A1BC1,BH 平面A1BC1,
所以D1P∥平面A1BC1;
(2),
根据题意可得三棱锥B1﹣A1BC1的体积为.
16.(2025春 城东区校级期中)如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥DC,AD⊥DC,DA=AB=2,DC=4,E,F分别为棱CD,PD的中点.
(1)求证:PB∥平面AEF;
(2)求证:AE⊥平面PBD.
(3)求证:平面AEF∥平面PBC.
【解答】证明:(1)如图,连接BE,设BD∩AE=O,连接OF,
因为AB∥DC,,
所以四边形ABED是平行四边形,
则OD=OB,又DF=PF,则OF∥PB,
因为OF 平面AEF,PB 平面AEF,
所以PB∥平面AEF;
(2)由四边形ABED是平行四边形,DA=AB=2,
所以四边形ABED为菱形,则AE⊥BD,
因为PD⊥平面ABCD,AE 平面ABCD,所以PD⊥AE,
又因为BD∩PD=D,BD、PD 平面PBD,
所以AE⊥平面PBD;
(3)由EC=DE,则EC=AB,又EC∥AB,
所以四边形ABCE是平行四边形,
故AE∥BC,又BC 平面AEF,AE 平面AEF,
所以BC∥平面AEF,
又PB∥平面AEF,PB∩BC=B,PB、BC 平面PBC,
所以平面AEF∥平面PBC.
17.(2025春 云南月考)在如图所示的几何体中,直线PD⊥底面ABCD,MA∥PD,底面ABCD是正方形,E,F,G分别为MB,PC,PB的中点,AD=PD=2.
(1)求证:PB⊥AC;
(2)求证:平面EFG∥平面ADPM;
(3)求直线PB与平面EFG所成角的正弦值.
【解答】解:(1)证明:连接BD,∵ABCD为正方形,∴AC⊥BD,
∵PD⊥底面ABCD,AC 平面ABCD,∴PD⊥AC,
∵BD∩PD=D,BD,PD 平面PBD,∴AC⊥平面PBD,
∵PB 平面PBD,∴AC⊥PB.
(2)证明:∵G,F分别为PB,PC的中点.∴GF∥BC,
∵BC∥AD,∴GF∥AD,
∵GF 平面ADPM,AD 平面ADPM,
∴GF∥平面ADPM,
同理可证GE∥平面ADPM,∵GF∩GE=G,GF、GE 平面EFG
∴平面EFG∥平面ADPM.
(3)∵PD⊥平面ABCD,AB 平面ABCD,∴PD⊥AB,
又AD⊥AB,PD∩AD=D,∴AB⊥平面ADPM,
连接PA,则∠APB为直线PB与平面ADPM所成的角,
∵AD=PD=2,∴,,
∴.
由(2)知平面EFG∥平面ADPM,
∴直线PB与平面EFG所成的角与PB与平面ADPM所成的角相等,
∴直线PB与平面EFG所成角的正弦值为.
18.(2025春 长春期中)如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点O为AC与BD的交点,点P为DD1的中点.
(1)求证:直线BD1∥平面PAC;
(2)求三棱锥B﹣PAC的体积.
【解答】解:(1)证明:如图,连接PO,
则O为BD中点,又点P为DD1的中点,
所以BD1∥PO,又BD1 平面PAC,PO 平面PAC,
所以BD1∥平面PAC;
(2)根据题意可得三棱锥B﹣PAC的体积为:
VB﹣PAC=VP﹣ABC.
19.(2025春 江北区校级期中)已知四棱锥P﹣ABCD的底面ABCD为是边长为1的正方形,PC⊥平面ABCD
(1)求证:BD⊥平面PAC;
(2)若PC=BC,平面PAB与平面PCD的交线为l,求直线l与直线PA所成角的余弦值;
(3)若E为PB中点,且直线DE与平面ABE所成角的正弦值为,求PC.
【解答】(1)证明:连接BD、AC,
∵PC⊥平面ABCD,BD 平面ABCD,∴PC⊥BD,
∵正方形ABCD中,AC⊥BD,且PC、AC是平面PAC内的相交直线,
∴BD⊥平面PAC.
(2)解:∵AB∥CD,CD 平面PCD,AB 平面PCD,∴AB∥平面PCD,
又∵AB 平面PAB,平面PAB∩平面PCD=l,∴l∥AB,
∴直线l与PA所成的角等于直线AB与PA所成的角,即∠PAB或其补角,
∵PC⊥平面ABCD,AB 平面ABCD,∴PC⊥AB,
∵AB⊥BC,PC、BC是平面PBC内的相交直线,
∴AB⊥平面PBC,结合PB 平面PBC,可得AB⊥PB,
∵Rt△PBC中,PC=BC=1,可得PB,Rt△PAB中,PA,可得,
∴直线l与直线PA所成角的余弦值为.
(3)解:在四棱锥P﹣ABCD中,PC⊥平面ABCD,四边形ABCD是正方形,
将四棱锥P﹣ABCD补形成正四棱柱PB1A1D1﹣CBAD,平面ABE即平面ABPD1,
在平面ADD1A1内,过点D作DF⊥AD1于F,连接EF,
∵AB⊥平面ADD1A1,DF 平面ADD1A1,∴DF⊥AB,
又∵AB∩AD1=A,AB、AD1 平面ABPD1,
∴DF⊥平面ABPD1,∠DEF是直线DE与平面ABE所成的角,
取BC中点G,连接DG、EG,
由E是BP的中点,可得EG∥PC,
∵EG⊥平面ABCD,DG 平面ABCD,∴EG⊥DG,
设PC=h,则,,则,
而,由直线DE与平面ABE所成角的正弦值为,
得,
整理得h4﹣6h2+5=0,解得h=1或,即PC=1或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年高三数学上学期专题突破练:立体几何初步
一.选择题(共8小题)
1.(2025春 浙江期中)下列说法正确的是( )
A.有两个面互相平行,其余各面都是平行四边形的几何体一定是棱柱
B.如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥可能为六棱锥
C.棱台的各侧棱延长后必交于一点
D.以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台
2.(2025春 长春期中)已知直角梯形ABCD中,AB⊥AD,AB∥CD,AB=6,CD=4,,则直角梯形ABCD的直观图A′B′C′D′的面积为( )
A.5 B. C.10 D.
3.(2025春 长安区校级期中)已知m,n表示不同的直线,α,β表示不同的平面,A表示点,则下列命题正确的是( )
A.若直线m上有无数个点在平面α内,则m∥α
B.若m α,n β,且α∥β,则m∥n
C.若m α,n β,则m∥n
D.若α∩β=m,且A∈α,A∈β,则A∈m
4.(2025秋 丽江月考)已知圆锥的轴截面为正三角形,且圆锥的体积为,若该圆锥的底面圆周和顶点都在同一球面上,则该球的表面积为( )
A. B.2π C.6π D.
5.(2025春 安徽月考)如图,已知在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2,AD=3,点E在棱BC上,且,则直线A1E与直线C1D1所成角的余弦值为( )
A. B. C. D.
6.(2025 杭州校级学业考试)在正四棱台ABCD﹣A1B1C1D1中,AB=2A1B1,AA1=2,且异面直线AA1与CD所成的角为60°,则该正四棱台的体积为( )
A. B. C. D.
7.(2025 海淀区校级模拟)如图,已知两个四棱锥P1﹣ABCD与P2﹣ABCD的公共底面是边长为2的正方形,顶点P1、P2在底面的同侧,棱锥的高P1O1=P2O2,O1、O2分别为AB、CD的中点,P1D与P2A交于点E,P1C与P2B交于点F.则四棱锥P1﹣ABFE的体积为( )
A. B. C. D.
8.(2025 惠州模拟)如图,ABC﹣A′B′C′为直三棱柱,用一个平行于底面ABC的平面α截此三棱柱,记下列三个三棱锥A′﹣ABC,A′﹣BCB′,A′﹣B′C′C在平面α上方的部位体积为V1,V2,V3,并记三个三棱锥被平面α截得的面积分别为S1,S2,S3,那么当V1+V3=2V2时,( )
A. B. C.1 D.
二.多选题(共3小题)
(多选)9.(2025春 长春期中)已知圆锥SO的母线长为4,其侧面积是底面积的2倍,则( )
A.该圆锥的表面积为12π
B.该圆锥的体积为
C.该圆锥侧面展开图为半圆
D.该圆锥轴截面为等边三角形
(多选)10.(2025春 重庆校级期中)已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
A.若m∥n,n α,m α,则m∥α
B.若m∥α,α∥β,则m∥β
C.若m∥α,n∥α,则m∥n
D.若α∥β,m α,则m∥β
(多选)11.(2025春 长春期中)半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体体现了数学的对称美.按照以下方式可构造一个半正多面体:如图,在一个棱长为4的正方体中,B1E1=B1F1=B1G1=a,A1E2=A1F2=A1G2=a,…,a∈(0,4),过E1,F1,G1三点可做一截面,类似地,可做8个形状完全相同的截面.关于该几何体,下列说法正确的是( )
A.当a=1时,该几何体是一个半正多面体
B.当a=3时,该几何体是一个半正多面体
C.若该几何体是由正八边形与正三角形围成的半正多面体,则边长为
D.若该几何体是由正方形与正三角形围成的半正多面体,则体积为32
三.填空题(共3小题)
12.(2025 枣庄校级二模)在三棱锥D﹣ABC中,△ABC是边长为的等边三角形,侧面DAB⊥底面ABC,∠ADB=120°.若三棱锥D﹣ABC的四个顶点均在同一球面上,则该球的表面积为 ,三棱锥D﹣ABC体积的最大值为 .
13.(2025春 丹东期末)已知等边△ABC的边长为,AD是BC边上的高,以AD为折痕将△ACD折起,使∠BDC=60°,则三棱锥A﹣BCD外接球的表面积为 .
14.(2025春 天津期中)阿基米德(Archimedes,公元前287年﹣公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为36π,则圆柱的表面积为 .
四.解答题(共5小题)
15.(2025春 长乐区校级期中)已知正方体ABCD﹣A1B1C1D1的棱长为2,P为AC的中点.
(1)证明:D1P∥平面A1BC1;
(2)求三棱锥B1﹣A1BC1的体积.
16.(2025春 城东区校级期中)如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥DC,AD⊥DC,DA=AB=2,DC=4,E,F分别为棱CD,PD的中点.
(1)求证:PB∥平面AEF;
(2)求证:AE⊥平面PBD.
(3)求证:平面AEF∥平面PBC.
17.(2025春 云南月考)在如图所示的几何体中,直线PD⊥底面ABCD,MA∥PD,底面ABCD是正方形,E,F,G分别为MB,PC,PB的中点,AD=PD=2.
(1)求证:PB⊥AC;
(2)求证:平面EFG∥平面ADPM;
(3)求直线PB与平面EFG所成角的正弦值.
18.(2025春 长春期中)如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点O为AC与BD的交点,点P为DD1的中点.
(1)求证:直线BD1∥平面PAC;
(2)求三棱锥B﹣PAC的体积.
19.(2025春 江北区校级期中)已知四棱锥P﹣ABCD的底面ABCD为是边长为1的正方形,PC⊥平面ABCD
(1)求证:BD⊥平面PAC;
(2)若PC=BC,平面PAB与平面PCD的交线为l,求直线l与直线PA所成角的余弦值;
(3)若E为PB中点,且直线DE与平面ABE所成角的正弦值为,求PC.
2026年高三数学上学期专题突破练:立体几何初步
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C A D D C B B B
二.多选题(共3小题)
题号 9 10 11
答案 ACD AD BC
一.选择题(共8小题)
1.(2025春 浙江期中)下列说法正确的是( )
A.有两个面互相平行,其余各面都是平行四边形的几何体一定是棱柱
B.如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥可能为六棱锥
C.棱台的各侧棱延长后必交于一点
D.以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台
【解答】解:根据题意,依次分析选项:
对于A,有两个面互相平行,其余各面都是平行四边形的几何体,若侧棱不平行,则不为棱柱,故A错误;
对于B,棱锥的各个侧面都是等边三角形,则顶角为60°,
若为六棱锥,则60°×6=360°,为一个周角,故为平面图形,故B错误;
对于C,由棱台的定义,棱台的各侧棱延长后必交于一点,C正确;
对于D,以直角梯形的一腰所在直线为轴旋转,如果旋转轴是梯形的斜边,则旋转体不是圆台,D错误.
故选:C.
2.(2025春 长春期中)已知直角梯形ABCD中,AB⊥AD,AB∥CD,AB=6,CD=4,,则直角梯形ABCD的直观图A′B′C′D′的面积为( )
A.5 B. C.10 D.
【解答】解:因为直角梯形ABCD中,AB⊥AD,AB∥CD,AB=6,CD=4,,
所以SABCD(6+4)10,
故直角梯形ABCD的直观图A′B′C′D′的面积为:SABCD105.
故选:A.
3.(2025春 长安区校级期中)已知m,n表示不同的直线,α,β表示不同的平面,A表示点,则下列命题正确的是( )
A.若直线m上有无数个点在平面α内,则m∥α
B.若m α,n β,且α∥β,则m∥n
C.若m α,n β,则m∥n
D.若α∩β=m,且A∈α,A∈β,则A∈m
【解答】解:已知m,n表示不同的直线,α,β表示不同的平面,A表示点,
对于A,若直线m上有无数个点在平面α内,
则m α,
即A错误;
对于B,若m α,n β,且α∥β,
则m∥n或m与n异面,
即B错误;
对于C,若m α,n β,
则m与n的位置关系不确定,
即C错误;
对于D,若α∩β=m,且A∈α,A∈β,
则A∈m,
即D正确.
故选:D.
4.(2025秋 丽江月考)已知圆锥的轴截面为正三角形,且圆锥的体积为,若该圆锥的底面圆周和顶点都在同一球面上,则该球的表面积为( )
A. B.2π C.6π D.
【解答】解:因为圆锥的轴截面为正三角形,且圆锥的体积为,
所以作出示意图如下:
设圆锥的底面半径为r,则圆锥的母线l=2r,高.
所以圆锥的体积为,解得,则,
设球的半径为R,球心到圆锥底面的距离为d,
则,即,解得,
所以球的表面积为.
故选:D.
5.(2025春 安徽月考)如图,已知在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2,AD=3,点E在棱BC上,且,则直线A1E与直线C1D1所成角的余弦值为( )
A. B. C. D.
【解答】解:以D为原点,分别以DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系,如图,
∴AA1=2AB=2,AD=3,则AB=1,AA1=2,
∴A1(3,0,2),C1(0,1,2),D1(0,0,2).
∵点E在棱BC上,且,BC=AD=3,
∴BE=2,EC=1,则E(1,1,0).
∴,
.
∴cos,
∵异面直线所成角的范围是,
∴直线A1E与直线C1D1所成角的余弦值为.
故选:C.
6.(2025 杭州校级学业考试)在正四棱台ABCD﹣A1B1C1D1中,AB=2A1B1,AA1=2,且异面直线AA1与CD所成的角为60°,则该正四棱台的体积为( )
A. B. C. D.
【解答】解:作出示意图如下:
∵AB∥CD,
∴异面直线AA1与CD所成的角为∠A1AB=60°,
过A1作A1M⊥AC于M,过M作MN⊥AB于N,
则A1M⊥AB,A1M⊥NM,
又A1M∩MN=M,
∴AB⊥平面A1MN,∴A1N⊥AB,
∵AB=2A1B1,AA1=2,∴,AN=AA1cos60°=1,
∴2A1B1=A1B1+2,∴A1B1=2,∴AB=4,
∵△ANM∽△ABC,∴,∴MN=1,∴,
∴该正四棱台的体积为:
.
故选:B.
7.(2025 海淀区校级模拟)如图,已知两个四棱锥P1﹣ABCD与P2﹣ABCD的公共底面是边长为2的正方形,顶点P1、P2在底面的同侧,棱锥的高P1O1=P2O2,O1、O2分别为AB、CD的中点,P1D与P2A交于点E,P1C与P2B交于点F.则四棱锥P1﹣ABFE的体积为( )
A. B. C. D.
【解答】解:连接P1P2,O1O2,O1D,如图所示.
因为P1O1平面ABCD,P2O2⊥平面ABCD,所以P1O1∥P2O2,
又P1O1=P2O2,所以四边形P1O1O2P2是矩形,所以P1P2∥O1O2,且P1P2=O1O2,
又O1,O2分别为AB,CD的中点,所以O1O2∥AD且O1O2=AD,
所以P1P2∥AD且P1P2=AD,所以四边形P1P2DA为平行四边形,
又对角线P2A∩DP1=E,所以E为P1D的中点.
连接P2O1,交EF于点N,过点P作P1M⊥P2O1于M,由题意知P2A=P2B,故P2O1⊥AB,
又P1O1⊥AB,P2O1∩P1O1=O1,P2O1,P1O1 平面P2P1O1,所以AB⊥平面P2P1O1.
因为P1M 平面P2P1O1,故AB⊥P1M.
又P2O1∩AB=O1,P2O1,AB 平面P2AB,所以P1M⊥平面P2AB,即P1M是四棱锥P1﹣ABFE的高,
同理可得点F为线段P1C的中点,所以EF∥CD,且,
在Rt△P2O2O1中,,则,
所以,
因为,
所以.
故选:B.
8.(2025 惠州模拟)如图,ABC﹣A′B′C′为直三棱柱,用一个平行于底面ABC的平面α截此三棱柱,记下列三个三棱锥A′﹣ABC,A′﹣BCB′,A′﹣B′C′C在平面α上方的部位体积为V1,V2,V3,并记三个三棱锥被平面α截得的面积分别为S1,S2,S3,那么当V1+V3=2V2时,( )
A. B. C.1 D.
【解答】解:如图所示,设直三棱柱的底面积为S,体积为V,
如图所示,,所以,
此时.
此时平面α在直棱柱的中间高度上,
故平面α与A′B,A′C,B′C相交于它们的中点处,此时截面如图所示:
可知,.
故选:B.
二.多选题(共3小题)
(多选)9.(2025春 长春期中)已知圆锥SO的母线长为4,其侧面积是底面积的2倍,则( )
A.该圆锥的表面积为12π
B.该圆锥的体积为
C.该圆锥侧面展开图为半圆
D.该圆锥轴截面为等边三角形
【解答】解:圆锥SO的母线长为4,其侧面积是底面积的2倍,
设圆锥底面半径为r,
则底面面积S1=πr2,底面周长C=2πr,
故侧面面积S2cl=4πr,
由题意得S2=2S1,即4πr=2πr2,即r=2,
故侧面面积S2cl=4πr=8π,可得表面积为:8π+4π=12π,A选项正确;
侧面面积S2=8ππ 42,所以该圆锥侧面展开图为半圆,C选项正确;
设该圆锥母线与底面所成角为α,则cosα,即α=60°,故圆锥轴截面为等边三角形,D选项正确;
则该圆锥的体积VS1hS1lsinα4π×4π,B选项不正确.
故选:ACD.
(多选)10.(2025春 重庆校级期中)已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
A.若m∥n,n α,m α,则m∥α
B.若m∥α,α∥β,则m∥β
C.若m∥α,n∥α,则m∥n
D.若α∥β,m α,则m∥β
【解答】解:若m∥n,n α,m α,则m∥α,所以A选项正确;
若m∥α,α∥β,则m∥β或m β,所以B选项错误;
若m∥α,n∥α,则m∥n或m与n相交或异面,所以C选项错误;
若α∥β,m α,则m∥β,所以D选项正确.
故选:AD.
(多选)11.(2025春 长春期中)半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体体现了数学的对称美.按照以下方式可构造一个半正多面体:如图,在一个棱长为4的正方体中,B1E1=B1F1=B1G1=a,A1E2=A1F2=A1G2=a,…,a∈(0,4),过E1,F1,G1三点可做一截面,类似地,可做8个形状完全相同的截面.关于该几何体,下列说法正确的是( )
A.当a=1时,该几何体是一个半正多面体
B.当a=3时,该几何体是一个半正多面体
C.若该几何体是由正八边形与正三角形围成的半正多面体,则边长为
D.若该几何体是由正方形与正三角形围成的半正多面体,则体积为32
【解答】解:对A选项,当a=1时,8个顶角的截面为等边三角形,但其余保留的每个面不是正八边形,所以A选项错误;
对B选项,当a=3时,8个顶角的截面为正六边形,其余保留的每个面是正方形,所以B选项正确;
对C选项,如图,因为棱长为4的正方体中,B1E1=B1F1=B1G1=a,A1E2=A1F2=A1G2=a,…,a∈(0,4),
所以,E1F2=4﹣2a,
当此半正多面体是由正八边形与正三角形围成时,,(,解得,故C正确;
对于D,当此半正多面体是由正方形与正三角形围成时,E1F2=4﹣2a=0,
所以a=2,表面积为,D错误.
故选:BC.
三.填空题(共3小题)
12.(2025 枣庄校级二模)在三棱锥D﹣ABC中,△ABC是边长为的等边三角形,侧面DAB⊥底面ABC,∠ADB=120°.若三棱锥D﹣ABC的四个顶点均在同一球面上,则该球的表面积为 5π ,三棱锥D﹣ABC体积的最大值为 .
【解答】解:如图①,设△ABC,△DAB的外接圆的圆心分别为O1,O2,半径为r1,r2,三棱锥D﹣ABC的外接球的球心为O,半径为R,
设AB的中点为E,则,即r1=1,同理可得r2=1.
因为侧面DAB⊥底面ABC,EO2⊥AB,可得EO2⊥底面ABC,所以EO2⊥EO1.
又OO1⊥底面ABC,OO2⊥侧面DAB,所以四边形OO1EO2为矩形.
在Rt△OO2A中,,
因为,所以,所以球O的表面积为5π.
设三棱锥D﹣ABC的高为h,过D作DH⊥AB于点H,
由面面垂直的性质可得,DH⊥底面ABC,即DH为三棱锥D﹣ABC的高.
△DAB及其外接圆如图②所示,由图可知,当D位于劣弧AB的中点时,h最大,最大值为,
所以三棱锥D﹣ABC体积的最大值为.
故答案为:5π;.
13.(2025春 丹东期末)已知等边△ABC的边长为,AD是BC边上的高,以AD为折痕将△ACD折起,使∠BDC=60°,则三棱锥A﹣BCD外接球的表面积为 52π .
【解答】解:根据题意作出示意图,如下图所示:
易知AD⊥DB,AD⊥DC,又BD∩DC=B,BD,DC 平面BDC,
所以AD⊥平面BDC,
设△BDC外接圆圆心为O1,过O1做面BDC垂线,
则垂线上所有点到△BDC顶点距离相等,且垂线与AD共面,
过A做上述垂线的垂线,垂足为O2,所以得四边形AO2O1D为矩形,
取O1O2中点为O,易知O为三棱锥A﹣BCD外接球球心,
所以AD=O1O2=6 OO1=3,
根据正弦定理有,
则OD满足,
所以外接球的表面积为.
故答案为:52π.
14.(2025春 天津期中)阿基米德(Archimedes,公元前287年﹣公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为36π,则圆柱的表面积为 54π .
【解答】解:设球的半径为r,则圆柱的底面半径也为r,高为2r,
所以球的体积公为,所以r=3,
所以圆柱的表面积为πr2×2+2πr 2r=6πr2=6π×9=54π.
故答案为:54π.
四.解答题(共5小题)
15.(2025春 长乐区校级期中)已知正方体ABCD﹣A1B1C1D1的棱长为2,P为AC的中点.
(1)证明:D1P∥平面A1BC1;
(2)求三棱锥B1﹣A1BC1的体积.
【解答】解:(1)证明:如图,设B1D1∩A1C1=H,连接BH,
因为DD1∥BB1,DD1=BB1,
所以四边形B1BDD1为平行四边形,
所以BD∥B1D1,
又P为AC的中点,H为B1D1的中点,
所以D1H∥BP,且D1H=BP,
所以四边形D1HBP是平行四边形,
所以BH∥D1P,又D1P 平面A1BC1,BH 平面A1BC1,
所以D1P∥平面A1BC1;
(2),
根据题意可得三棱锥B1﹣A1BC1的体积为.
16.(2025春 城东区校级期中)如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥DC,AD⊥DC,DA=AB=2,DC=4,E,F分别为棱CD,PD的中点.
(1)求证:PB∥平面AEF;
(2)求证:AE⊥平面PBD.
(3)求证:平面AEF∥平面PBC.
【解答】证明:(1)如图,连接BE,设BD∩AE=O,连接OF,
因为AB∥DC,,
所以四边形ABED是平行四边形,
则OD=OB,又DF=PF,则OF∥PB,
因为OF 平面AEF,PB 平面AEF,
所以PB∥平面AEF;
(2)由四边形ABED是平行四边形,DA=AB=2,
所以四边形ABED为菱形,则AE⊥BD,
因为PD⊥平面ABCD,AE 平面ABCD,所以PD⊥AE,
又因为BD∩PD=D,BD、PD 平面PBD,
所以AE⊥平面PBD;
(3)由EC=DE,则EC=AB,又EC∥AB,
所以四边形ABCE是平行四边形,
故AE∥BC,又BC 平面AEF,AE 平面AEF,
所以BC∥平面AEF,
又PB∥平面AEF,PB∩BC=B,PB、BC 平面PBC,
所以平面AEF∥平面PBC.
17.(2025春 云南月考)在如图所示的几何体中,直线PD⊥底面ABCD,MA∥PD,底面ABCD是正方形,E,F,G分别为MB,PC,PB的中点,AD=PD=2.
(1)求证:PB⊥AC;
(2)求证:平面EFG∥平面ADPM;
(3)求直线PB与平面EFG所成角的正弦值.
【解答】解:(1)证明:连接BD,∵ABCD为正方形,∴AC⊥BD,
∵PD⊥底面ABCD,AC 平面ABCD,∴PD⊥AC,
∵BD∩PD=D,BD,PD 平面PBD,∴AC⊥平面PBD,
∵PB 平面PBD,∴AC⊥PB.
(2)证明:∵G,F分别为PB,PC的中点.∴GF∥BC,
∵BC∥AD,∴GF∥AD,
∵GF 平面ADPM,AD 平面ADPM,
∴GF∥平面ADPM,
同理可证GE∥平面ADPM,∵GF∩GE=G,GF、GE 平面EFG
∴平面EFG∥平面ADPM.
(3)∵PD⊥平面ABCD,AB 平面ABCD,∴PD⊥AB,
又AD⊥AB,PD∩AD=D,∴AB⊥平面ADPM,
连接PA,则∠APB为直线PB与平面ADPM所成的角,
∵AD=PD=2,∴,,
∴.
由(2)知平面EFG∥平面ADPM,
∴直线PB与平面EFG所成的角与PB与平面ADPM所成的角相等,
∴直线PB与平面EFG所成角的正弦值为.
18.(2025春 长春期中)如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点O为AC与BD的交点,点P为DD1的中点.
(1)求证:直线BD1∥平面PAC;
(2)求三棱锥B﹣PAC的体积.
【解答】解:(1)证明:如图,连接PO,
则O为BD中点,又点P为DD1的中点,
所以BD1∥PO,又BD1 平面PAC,PO 平面PAC,
所以BD1∥平面PAC;
(2)根据题意可得三棱锥B﹣PAC的体积为:
VB﹣PAC=VP﹣ABC.
19.(2025春 江北区校级期中)已知四棱锥P﹣ABCD的底面ABCD为是边长为1的正方形,PC⊥平面ABCD
(1)求证:BD⊥平面PAC;
(2)若PC=BC,平面PAB与平面PCD的交线为l,求直线l与直线PA所成角的余弦值;
(3)若E为PB中点,且直线DE与平面ABE所成角的正弦值为,求PC.
【解答】(1)证明:连接BD、AC,
∵PC⊥平面ABCD,BD 平面ABCD,∴PC⊥BD,
∵正方形ABCD中,AC⊥BD,且PC、AC是平面PAC内的相交直线,
∴BD⊥平面PAC.
(2)解:∵AB∥CD,CD 平面PCD,AB 平面PCD,∴AB∥平面PCD,
又∵AB 平面PAB,平面PAB∩平面PCD=l,∴l∥AB,
∴直线l与PA所成的角等于直线AB与PA所成的角,即∠PAB或其补角,
∵PC⊥平面ABCD,AB 平面ABCD,∴PC⊥AB,
∵AB⊥BC,PC、BC是平面PBC内的相交直线,
∴AB⊥平面PBC,结合PB 平面PBC,可得AB⊥PB,
∵Rt△PBC中,PC=BC=1,可得PB,Rt△PAB中,PA,可得,
∴直线l与直线PA所成角的余弦值为.
(3)解:在四棱锥P﹣ABCD中,PC⊥平面ABCD,四边形ABCD是正方形,
将四棱锥P﹣ABCD补形成正四棱柱PB1A1D1﹣CBAD,平面ABE即平面ABPD1,
在平面ADD1A1内,过点D作DF⊥AD1于F,连接EF,
∵AB⊥平面ADD1A1,DF 平面ADD1A1,∴DF⊥AB,
又∵AB∩AD1=A,AB、AD1 平面ABPD1,
∴DF⊥平面ABPD1,∠DEF是直线DE与平面ABE所成的角,
取BC中点G,连接DG、EG,
由E是BP的中点,可得EG∥PC,
∵EG⊥平面ABCD,DG 平面ABCD,∴EG⊥DG,
设PC=h,则,,则,
而,由直线DE与平面ABE所成角的正弦值为,
得,
整理得h4﹣6h2+5=0,解得h=1或,即PC=1或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
