2026年高三数学上学期专题突破练:三角函数(含解析)
文档属性
| 名称 | 2026年高三数学上学期专题突破练:三角函数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 787.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-11 11:32:07 | ||
图片预览


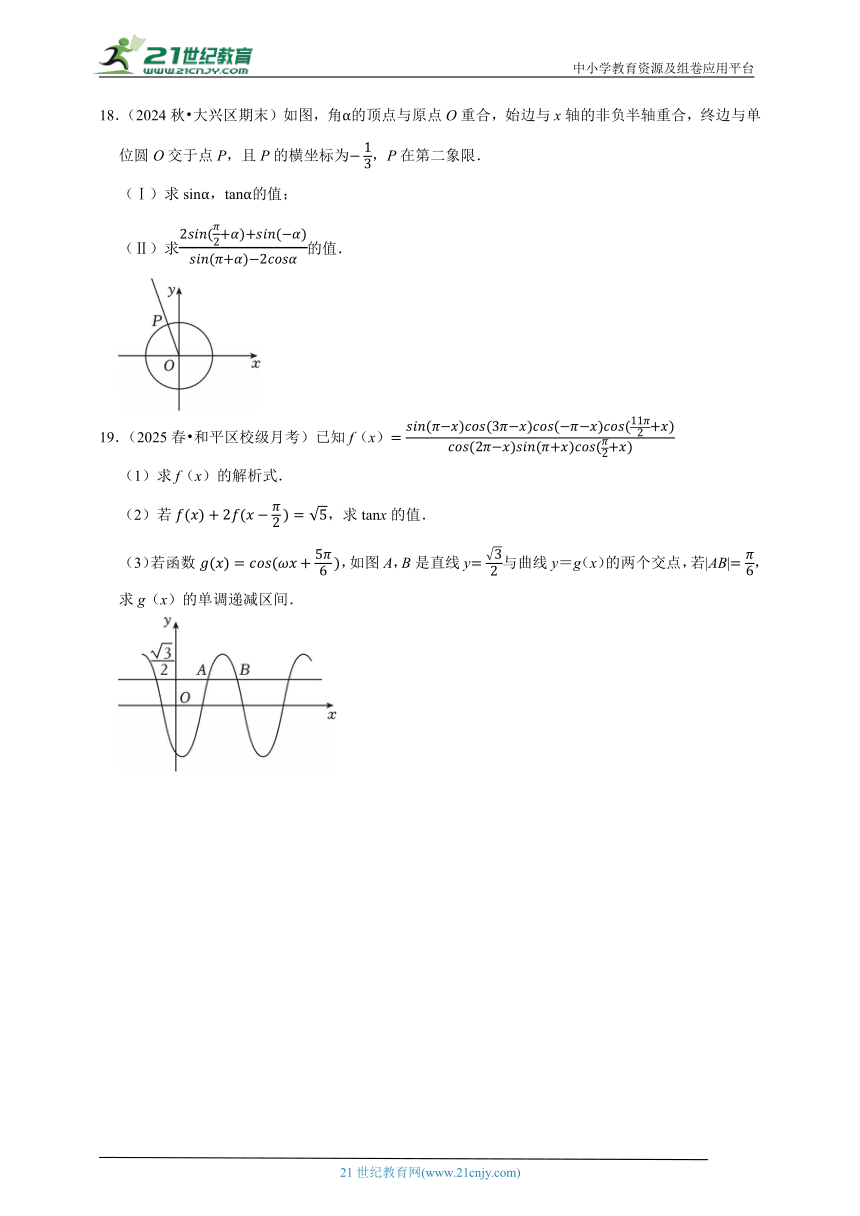

文档简介
中小学教育资源及组卷应用平台
2026年高三数学上学期专题突破练:三角函数
一.选择题(共8小题)
1.(2024秋 天津期末)sin240°=( )
A. B. C. D.
2.(2025春 红桥区校级期中)若一个扇形的弧长为4,面积为16,则这个扇形圆心角的弧度数是( )
A.4 B.3 C.2 D.
3.(2025 广州模拟)已知ω>0,曲线y=cosωx与相邻的三个交点构成一个直角三角形,则ω=( )
A. B. C. D.
4.(2025春 湖南期中)已知锐角α满足,则tan2α=( )
A. B. C. D.﹣1
5.(2025春 金山区校级期中)对于函数y=f(x),f(x)=3cos2x的图像( )得到.
A.向右平移 B.向右平移
C.向右平移 D.向右平移
6.(2025春 湖南期中)已知ω>0,函数的最小正周期为T,若π<T<2π,且f(x)的图象关于直线对称,则( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
7.(2024秋 西湖区校级期末)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的部分图象如图所示,则f(1)+f(2)+f(3)+ +f(2024)等于( )
A. B.0 C. D.
8.(2025春 沙市区校级月考)已知函数f(x)=|cosx| sinx,给出下列四个说法:
①;②;
③f(x)在区间上单调递增;④f(x)的图象关于点中心对称.
其中正确说法的序号是( )
A.②③ B.①③ C.①④ D.①③④
二.多选题(共3小题)
(多选)9.(2025春 凤城市校级期中)下列说法正确的是( )
A.若α终边上一点的坐标为(3k,4k)(k≠0),则
B.若角α为锐角,则2α为钝角
C.若圆心角为的扇形的弧长为π,则该扇形的面积为
D.若,且0<α<π,则
(多选)10.(2025春 云南月考)关于函数f(x)=sin2x和,则下列说法中正确的是( )
A.函数f(x)和g(x)有相同的最小值
B.存在直线l,使函数f(x)和g(x)的图象都关于直线l对称
C.存在点P,使函数f(x)和g(x)的图象都关于点P对称
D.函数F(x)=f(x)﹣g(x),x∈[0,4π]有6个零点
(多选)11.(2025 长沙校级一模)已知函数f(x)=sinωx+acosωx(ω>0)的最大值为,其部分图象如图所示,则( )
A.ω=1
B.函数为偶函数
C.y=f(x)在[0,m]上有4个零点,则
D.当时,函数的值域为
三.填空题(共3小题)
12.(2025春 金山区校级期中)已知,则cos(π﹣α)= .
13.(2025春 沙市区校级月考)已知α,β均为锐角,且满足3sin2α+2sin2β=1,3sin2α﹣2sin2β=0,则α+2β值为 .
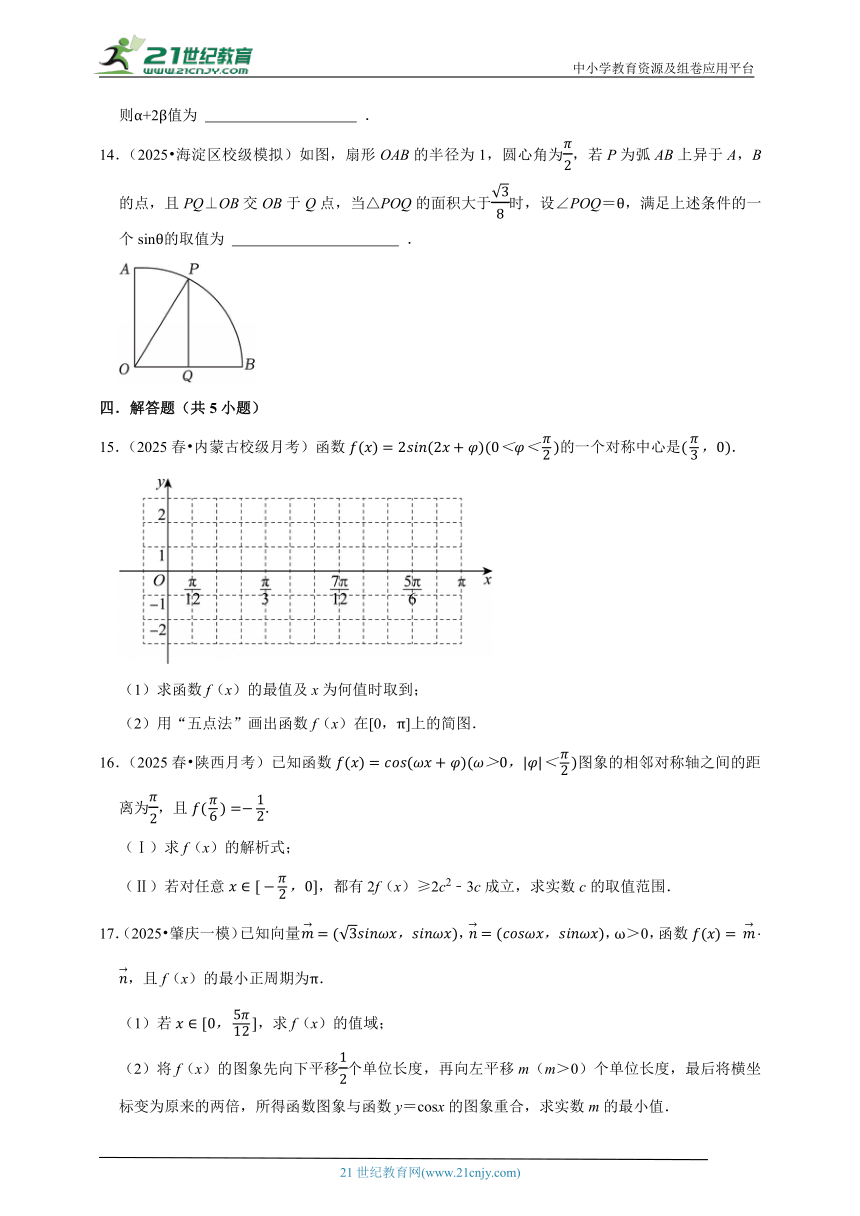
14.(2025 海淀区校级模拟)如图,扇形OAB的半径为1,圆心角为,若P为弧AB上异于A,B的点,且PQ⊥OB交OB于Q点,当△POQ的面积大于时,设∠POQ=θ,满足上述条件的一个sinθ的取值为 .
四.解答题(共5小题)
15.(2025春 内蒙古校级月考)函数的一个对称中心是.
(1)求函数f(x)的最值及x为何值时取到;
(2)用“五点法”画出函数f(x)在[0,π]上的简图.
16.(2025春 陕西月考)已知函数图象的相邻对称轴之间的距离为,且.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若对任意,都有2f(x)≥2c2﹣3c成立,求实数c的取值范围.
17.(2025 肇庆一模)已知向量,,ω>0,函数,且f(x)的最小正周期为π.
(1)若,求f(x)的值域;
(2)将f(x)的图象先向下平移个单位长度,再向左平移m(m>0)个单位长度,最后将横坐标变为原来的两倍,所得函数图象与函数y=cosx的图象重合,求实数m的最小值.
18.(2024秋 大兴区期末)如图,角α的顶点与原点O重合,始边与x轴的非负半轴重合,终边与单位圆O交于点P,且P的横坐标为,P在第二象限.
(Ⅰ)求sinα,tanα的值;
(Ⅱ)求的值.
19.(2025春 和平区校级月考)已知f(x)
(1)求f(x)的解析式.
(2)若,求tanx的值.
(3)若函数,如图A,B是直线y与曲线y=g(x)的两个交点,若|AB|,求g(x)的单调递减区间.
2026年高三数学上学期专题突破练:三角函数
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A D A C A D B B
二.多选题(共3小题)
题号 9 10 11
答案 CD ABD ABC
一.选择题(共8小题)
1.(2024秋 天津期末)sin240°=( )
A. B. C. D.
【解答】解:sin240°=sin(180°+60°)=﹣sin60°,
故选:A.
2.(2025春 红桥区校级期中)若一个扇形的弧长为4,面积为16,则这个扇形圆心角的弧度数是( )
A.4 B.3 C.2 D.
【解答】解:设扇形圆心角的弧度为θ,半径为r,
由于扇形的弧长为4,面积为16,
则,解得.
故选:D.
3.(2025 广州模拟)已知ω>0,曲线y=cosωx与相邻的三个交点构成一个直角三角形,则ω=( )
A. B. C. D.
【解答】解:设曲线y=cosωx与相邻的三个交点分别为A(x1,y1),B(x2,y2),C(x3,y3),
由cosωx=cos(ωx)cosωxsinωx,可得sinωxcosωx=0,
即sin(ωx)=0,解得(k∈Z),
不妨取k=0、1、2,解得,,,所以,,.
可得AB2=BC2,,
根据△ABC为直角三角形,可得AB2+BC2=AC2,即,解得.
故选:A.
4.(2025春 湖南期中)已知锐角α满足,则tan2α=( )
A. B. C. D.﹣1
【解答】解:根据,α∈(0,),可得,
所以,可得.
故选:C.
5.(2025春 金山区校级期中)对于函数y=f(x),f(x)=3cos2x的图像( )得到.
A.向右平移 B.向右平移
C.向右平移 D.向右平移
【解答】解:将f(x)=3cos2x向右平移个单位可得函数f(x)=3cos(2x)的图象.
故选:A.
6.(2025春 湖南期中)已知ω>0,函数的最小正周期为T,若π<T<2π,且f(x)的图象关于直线对称,则( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
【解答】解:函数的最小正周期为T,
因为π<T<2π,所以,解得1<ω<2.
又f(x)的图象关于直线对称,所以π<T<2π,
解得.
因为1<ω<2,
取k=0,可得,
所以f(x)=cos()﹣3,故f()=cos()﹣3=﹣4.
故选:D.
7.(2024秋 西湖区校级期末)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的部分图象如图所示,则f(1)+f(2)+f(3)+ +f(2024)等于( )
A. B.0 C. D.
【解答】解:由图象可知,A=2,T=8,故,f(x)=2sin(x+φ),
又f(0)=0且,∴φ=0,故.
又根据函数的对称性可知,f(2)=﹣f(6)=2,f(4)=f(8)=0,
所以f(1)+f(2)+f(3)+ +f(8)=0,
所以f(1)+f(2)+f(3)+ +f(2024)=253×[f(1)+f(2)+f(3)+ +f(8)]=0.
故选:B.
8.(2025春 沙市区校级月考)已知函数f(x)=|cosx| sinx,给出下列四个说法:
①;②;
③f(x)在区间上单调递增;④f(x)的图象关于点中心对称.
其中正确说法的序号是( )
A.②③ B.①③ C.①④ D.①③④
【解答】解:分析①:,周期为2π,故.
,则;.
因此,①正确.
分析②:.
.
故,②错误.
分析③:当时,cosx≥0,则.
令t=2x,,sint在上单调递增,故f(x)在此区间单调递增,③正确.
分析④:验证中心对称需.
取,,.
和为﹣1≠0,不关于中心对称,④错误.
综上,①③正确.
故选:B.
二.多选题(共3小题)
(多选)9.(2025春 凤城市校级期中)下列说法正确的是( )
A.若α终边上一点的坐标为(3k,4k)(k≠0),则
B.若角α为锐角,则2α为钝角
C.若圆心角为的扇形的弧长为π,则该扇形的面积为
D.若,且0<α<π,则
【解答】解:对于A,点(3k,4k)(k≠0)到原点的距离为r=5|k|,
若k<0,则,若k>0,则,故A错误;
对于B,若是锐角,但还是锐角,故B错误;
对于C,圆心角为的扇形的弧长为π,设扇形的半径为r,则,解得r=3,所以扇形的面积,故C正确;
对于D,因为,且0<α<π,
即,所以,
所以,解得或,
因为,,所以|sinα|>|cosα|,所以,故D正确.
故选:CD.
(多选)10.(2025春 云南月考)关于函数f(x)=sin2x和,则下列说法中正确的是( )
A.函数f(x)和g(x)有相同的最小值
B.存在直线l,使函数f(x)和g(x)的图象都关于直线l对称
C.存在点P,使函数f(x)和g(x)的图象都关于点P对称
D.函数F(x)=f(x)﹣g(x),x∈[0,4π]有6个零点
【解答】解:对于A,f(x)与g(x)的最小值为1,故A正确;
对于B,函数f(x)=sin2x的对称轴为,k1∈Z,
所以,k1∈Z,
的对称轴为,
所以,k2∈Z,可知,是函数f(x)和g(x)的对称轴,故B正确;
对于C,函数f(x)=sin2x的对称中心为2x3=k3π,k3∈Z,所以,k3∈Z,
的对称中心为,所以,k4∈Z,
令,则,
不存在k3,k4∈Z,成立,故C错误;
对于D,令F(x)=f(x)﹣g(x)=0,即f(x)=g(x),
即,即,
,解得或1,
x∈[0,4π],则,
当时,或,
解得或,
当时,或或或,
解得或或或,
所以函数F(x)=f(x)﹣g(x),x∈[0,4π]有6个零点,故D正确.
故选:ABD.
(多选)11.(2025 长沙校级一模)已知函数f(x)=sinωx+acosωx(ω>0)的最大值为,其部分图象如图所示,则( )
A.ω=1
B.函数为偶函数
C.y=f(x)在[0,m]上有4个零点,则
D.当时,函数的值域为
【解答】解:对于选项A:因为,
可得f(x)的最小正周期,
又ω>0,
所以ω=1,
所以f(x)=sinx+acosx,故A正确;
对于选项B:因为当时,函数y=f(x)取到最大值,
所以,解得a=﹣1,
可得,
可得为偶函数,故B正确;
对于选项C:令,可得,
因为x∈[0,m],则,
若y=f(x)在[0,m]上有4个零点,
则,解得,故C正确;
对于选项D:由于,
又,
可得,则,
可得的值域为,故D错误.
故选:ABC.
三.填空题(共3小题)
12.(2025春 金山区校级期中)已知,则cos(π﹣α)= .
【解答】解:由cosα,
,得,
∴cos(π﹣α)=﹣cosα.
故答案为:.
13.(2025春 沙市区校级月考)已知α,β均为锐角,且满足3sin2α+2sin2β=1,3sin2α﹣2sin2β=0,则α+2β值为 .
【解答】解:∵3sin2α+2sin2β=1,∴3sin2α=1﹣2sin2β=cos2β,
∵3sin2α﹣2sin2β=0,∴3sinαcosα=sin2β,
两式相除得:,
∴cosαcos2β﹣sinαsin2β=cos(α+2β)=0,
∵α,β均为锐角,
∴,
∴.
故答案为:.
14.(2025 海淀区校级模拟)如图,扇形OAB的半径为1,圆心角为,若P为弧AB上异于A,B的点,且PQ⊥OB交OB于Q点,当△POQ的面积大于时,设∠POQ=θ,满足上述条件的一个sinθ的取值为 (答案不唯一) .
【解答】解:由已知,OQ=cosθ,OP=1,所以△POQ的面积S,
由△POQ的面积大于,得,即sin2θ,
因为0<θ,所以解得2θ,θ,故sinθ,可取.
故答案为:(答案不唯一).
四.解答题(共5小题)
15.(2025春 内蒙古校级月考)函数的一个对称中心是.
(1)求函数f(x)的最值及x为何值时取到;
(2)用“五点法”画出函数f(x)在[0,π]上的简图.
【解答】解:(1)由题意得,
则,解得,
因为,所以k=1时,,
所以,其最大值为2,最小值为﹣2,
当,即时,函数f(x)取得最大值2;
当,即时,函数f(x)取得最小值﹣2.
(2)列表如下:
π 2π
x 0 π
y 2 0 ﹣2 0
函数f(x)在[0,π]上的简图如下,
16.(2025春 陕西月考)已知函数图象的相邻对称轴之间的距离为,且.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若对任意,都有2f(x)≥2c2﹣3c成立,求实数c的取值范围.
【解答】解:(1)函数图象的相邻对称轴之间的距离为,由函数f(x)图象的相邻对称轴之间的距离为,可得,
∴,可得ω=2,
又,可得,∵,
∴解得,
∴f(x)的解析式为.
(2)当时,,
∴,
∵对任意,都有2f(x)≥2c2﹣3c成立,
∴,即2c2﹣3c≤﹣1,解得.
∴实数c的取值范围为.
17.(2025 肇庆一模)已知向量,,ω>0,函数,且f(x)的最小正周期为π.
(1)若,求f(x)的值域;
(2)将f(x)的图象先向下平移个单位长度,再向左平移m(m>0)个单位长度,最后将横坐标变为原来的两倍,所得函数图象与函数y=cosx的图象重合,求实数m的最小值.
【解答】解:(1)向量,,ω>0,
则
,
因为f(x)最小正周期为π,所以,解得ω=1,
所以,
因为,所以,
则,
所以,
所以当时,f(x)的值域为.
(2)向下平移个单位长度得,
向左平移m(m>0)个单位长度得,
横坐标变为原来的2倍得.
因为,
所以要使得与y=cosx的图象重合,
则,k∈Z,解得,k∈Z
当k=0时,实数m取得最小值.
18.(2024秋 大兴区期末)如图,角α的顶点与原点O重合,始边与x轴的非负半轴重合,终边与单位圆O交于点P,且P的横坐标为,P在第二象限.
(Ⅰ)求sinα,tanα的值;
(Ⅱ)求的值.
【解答】解:(Ⅰ)因为P的横坐标为,P在第二象限,
所以P的纵坐标为,即P(,),
所以sinα,tanα2.
(Ⅱ)3+2.
19.(2025春 和平区校级月考)已知f(x)
(1)求f(x)的解析式.
(2)若,求tanx的值.
(3)若函数,如图A,B是直线y与曲线y=g(x)的两个交点,若|AB|,求g(x)的单调递减区间.
【解答】解:(1)依题意,,
由sinxcosx≠0得,k∈Z,
所以f(x)的解析式为.
(2)由(1)及,得,则,
两边平方得4sin2x+4sinxcosx+cos2x=5﹣5sin2x+5cos2x,
整理得(sinx﹣2cosx)2=0,因此sinx=2cosx,所以tanx=2.
(3)由,得,,k1,k∈Z,
由,得,因此,解得ω=2,,
由,k∈Z,解得,k∈Z,
所以g(x)的单调递减区间为,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年高三数学上学期专题突破练:三角函数
一.选择题(共8小题)
1.(2024秋 天津期末)sin240°=( )
A. B. C. D.
2.(2025春 红桥区校级期中)若一个扇形的弧长为4,面积为16,则这个扇形圆心角的弧度数是( )
A.4 B.3 C.2 D.
3.(2025 广州模拟)已知ω>0,曲线y=cosωx与相邻的三个交点构成一个直角三角形,则ω=( )
A. B. C. D.
4.(2025春 湖南期中)已知锐角α满足,则tan2α=( )
A. B. C. D.﹣1
5.(2025春 金山区校级期中)对于函数y=f(x),f(x)=3cos2x的图像( )得到.
A.向右平移 B.向右平移
C.向右平移 D.向右平移
6.(2025春 湖南期中)已知ω>0,函数的最小正周期为T,若π<T<2π,且f(x)的图象关于直线对称,则( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
7.(2024秋 西湖区校级期末)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的部分图象如图所示,则f(1)+f(2)+f(3)+ +f(2024)等于( )
A. B.0 C. D.
8.(2025春 沙市区校级月考)已知函数f(x)=|cosx| sinx,给出下列四个说法:
①;②;
③f(x)在区间上单调递增;④f(x)的图象关于点中心对称.
其中正确说法的序号是( )
A.②③ B.①③ C.①④ D.①③④
二.多选题(共3小题)
(多选)9.(2025春 凤城市校级期中)下列说法正确的是( )
A.若α终边上一点的坐标为(3k,4k)(k≠0),则
B.若角α为锐角,则2α为钝角
C.若圆心角为的扇形的弧长为π,则该扇形的面积为
D.若,且0<α<π,则
(多选)10.(2025春 云南月考)关于函数f(x)=sin2x和,则下列说法中正确的是( )
A.函数f(x)和g(x)有相同的最小值
B.存在直线l,使函数f(x)和g(x)的图象都关于直线l对称
C.存在点P,使函数f(x)和g(x)的图象都关于点P对称
D.函数F(x)=f(x)﹣g(x),x∈[0,4π]有6个零点
(多选)11.(2025 长沙校级一模)已知函数f(x)=sinωx+acosωx(ω>0)的最大值为,其部分图象如图所示,则( )
A.ω=1
B.函数为偶函数
C.y=f(x)在[0,m]上有4个零点,则
D.当时,函数的值域为
三.填空题(共3小题)
12.(2025春 金山区校级期中)已知,则cos(π﹣α)= .
13.(2025春 沙市区校级月考)已知α,β均为锐角,且满足3sin2α+2sin2β=1,3sin2α﹣2sin2β=0,则α+2β值为 .
14.(2025 海淀区校级模拟)如图,扇形OAB的半径为1,圆心角为,若P为弧AB上异于A,B的点,且PQ⊥OB交OB于Q点,当△POQ的面积大于时,设∠POQ=θ,满足上述条件的一个sinθ的取值为 .
四.解答题(共5小题)
15.(2025春 内蒙古校级月考)函数的一个对称中心是.
(1)求函数f(x)的最值及x为何值时取到;
(2)用“五点法”画出函数f(x)在[0,π]上的简图.
16.(2025春 陕西月考)已知函数图象的相邻对称轴之间的距离为,且.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若对任意,都有2f(x)≥2c2﹣3c成立,求实数c的取值范围.
17.(2025 肇庆一模)已知向量,,ω>0,函数,且f(x)的最小正周期为π.
(1)若,求f(x)的值域;
(2)将f(x)的图象先向下平移个单位长度,再向左平移m(m>0)个单位长度,最后将横坐标变为原来的两倍,所得函数图象与函数y=cosx的图象重合,求实数m的最小值.
18.(2024秋 大兴区期末)如图,角α的顶点与原点O重合,始边与x轴的非负半轴重合,终边与单位圆O交于点P,且P的横坐标为,P在第二象限.
(Ⅰ)求sinα,tanα的值;
(Ⅱ)求的值.
19.(2025春 和平区校级月考)已知f(x)
(1)求f(x)的解析式.
(2)若,求tanx的值.
(3)若函数,如图A,B是直线y与曲线y=g(x)的两个交点,若|AB|,求g(x)的单调递减区间.
2026年高三数学上学期专题突破练:三角函数
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A D A C A D B B
二.多选题(共3小题)
题号 9 10 11
答案 CD ABD ABC
一.选择题(共8小题)
1.(2024秋 天津期末)sin240°=( )
A. B. C. D.
【解答】解:sin240°=sin(180°+60°)=﹣sin60°,
故选:A.
2.(2025春 红桥区校级期中)若一个扇形的弧长为4,面积为16,则这个扇形圆心角的弧度数是( )
A.4 B.3 C.2 D.
【解答】解:设扇形圆心角的弧度为θ,半径为r,
由于扇形的弧长为4,面积为16,
则,解得.
故选:D.
3.(2025 广州模拟)已知ω>0,曲线y=cosωx与相邻的三个交点构成一个直角三角形,则ω=( )
A. B. C. D.
【解答】解:设曲线y=cosωx与相邻的三个交点分别为A(x1,y1),B(x2,y2),C(x3,y3),
由cosωx=cos(ωx)cosωxsinωx,可得sinωxcosωx=0,
即sin(ωx)=0,解得(k∈Z),
不妨取k=0、1、2,解得,,,所以,,.
可得AB2=BC2,,
根据△ABC为直角三角形,可得AB2+BC2=AC2,即,解得.
故选:A.
4.(2025春 湖南期中)已知锐角α满足,则tan2α=( )
A. B. C. D.﹣1
【解答】解:根据,α∈(0,),可得,
所以,可得.
故选:C.
5.(2025春 金山区校级期中)对于函数y=f(x),f(x)=3cos2x的图像( )得到.
A.向右平移 B.向右平移
C.向右平移 D.向右平移
【解答】解:将f(x)=3cos2x向右平移个单位可得函数f(x)=3cos(2x)的图象.
故选:A.
6.(2025春 湖南期中)已知ω>0,函数的最小正周期为T,若π<T<2π,且f(x)的图象关于直线对称,则( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
【解答】解:函数的最小正周期为T,
因为π<T<2π,所以,解得1<ω<2.
又f(x)的图象关于直线对称,所以π<T<2π,
解得.
因为1<ω<2,
取k=0,可得,
所以f(x)=cos()﹣3,故f()=cos()﹣3=﹣4.
故选:D.
7.(2024秋 西湖区校级期末)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的部分图象如图所示,则f(1)+f(2)+f(3)+ +f(2024)等于( )
A. B.0 C. D.
【解答】解:由图象可知,A=2,T=8,故,f(x)=2sin(x+φ),
又f(0)=0且,∴φ=0,故.
又根据函数的对称性可知,f(2)=﹣f(6)=2,f(4)=f(8)=0,
所以f(1)+f(2)+f(3)+ +f(8)=0,
所以f(1)+f(2)+f(3)+ +f(2024)=253×[f(1)+f(2)+f(3)+ +f(8)]=0.
故选:B.
8.(2025春 沙市区校级月考)已知函数f(x)=|cosx| sinx,给出下列四个说法:
①;②;
③f(x)在区间上单调递增;④f(x)的图象关于点中心对称.
其中正确说法的序号是( )
A.②③ B.①③ C.①④ D.①③④
【解答】解:分析①:,周期为2π,故.
,则;.
因此,①正确.
分析②:.
.
故,②错误.
分析③:当时,cosx≥0,则.
令t=2x,,sint在上单调递增,故f(x)在此区间单调递增,③正确.
分析④:验证中心对称需.
取,,.
和为﹣1≠0,不关于中心对称,④错误.
综上,①③正确.
故选:B.
二.多选题(共3小题)
(多选)9.(2025春 凤城市校级期中)下列说法正确的是( )
A.若α终边上一点的坐标为(3k,4k)(k≠0),则
B.若角α为锐角,则2α为钝角
C.若圆心角为的扇形的弧长为π,则该扇形的面积为
D.若,且0<α<π,则
【解答】解:对于A,点(3k,4k)(k≠0)到原点的距离为r=5|k|,
若k<0,则,若k>0,则,故A错误;
对于B,若是锐角,但还是锐角,故B错误;
对于C,圆心角为的扇形的弧长为π,设扇形的半径为r,则,解得r=3,所以扇形的面积,故C正确;
对于D,因为,且0<α<π,
即,所以,
所以,解得或,
因为,,所以|sinα|>|cosα|,所以,故D正确.
故选:CD.
(多选)10.(2025春 云南月考)关于函数f(x)=sin2x和,则下列说法中正确的是( )
A.函数f(x)和g(x)有相同的最小值
B.存在直线l,使函数f(x)和g(x)的图象都关于直线l对称
C.存在点P,使函数f(x)和g(x)的图象都关于点P对称
D.函数F(x)=f(x)﹣g(x),x∈[0,4π]有6个零点
【解答】解:对于A,f(x)与g(x)的最小值为1,故A正确;
对于B,函数f(x)=sin2x的对称轴为,k1∈Z,
所以,k1∈Z,
的对称轴为,
所以,k2∈Z,可知,是函数f(x)和g(x)的对称轴,故B正确;
对于C,函数f(x)=sin2x的对称中心为2x3=k3π,k3∈Z,所以,k3∈Z,
的对称中心为,所以,k4∈Z,
令,则,
不存在k3,k4∈Z,成立,故C错误;
对于D,令F(x)=f(x)﹣g(x)=0,即f(x)=g(x),
即,即,
,解得或1,
x∈[0,4π],则,
当时,或,
解得或,
当时,或或或,
解得或或或,
所以函数F(x)=f(x)﹣g(x),x∈[0,4π]有6个零点,故D正确.
故选:ABD.
(多选)11.(2025 长沙校级一模)已知函数f(x)=sinωx+acosωx(ω>0)的最大值为,其部分图象如图所示,则( )
A.ω=1
B.函数为偶函数
C.y=f(x)在[0,m]上有4个零点,则
D.当时,函数的值域为
【解答】解:对于选项A:因为,
可得f(x)的最小正周期,
又ω>0,
所以ω=1,
所以f(x)=sinx+acosx,故A正确;
对于选项B:因为当时,函数y=f(x)取到最大值,
所以,解得a=﹣1,
可得,
可得为偶函数,故B正确;
对于选项C:令,可得,
因为x∈[0,m],则,
若y=f(x)在[0,m]上有4个零点,
则,解得,故C正确;
对于选项D:由于,
又,
可得,则,
可得的值域为,故D错误.
故选:ABC.
三.填空题(共3小题)
12.(2025春 金山区校级期中)已知,则cos(π﹣α)= .
【解答】解:由cosα,
,得,
∴cos(π﹣α)=﹣cosα.
故答案为:.
13.(2025春 沙市区校级月考)已知α,β均为锐角,且满足3sin2α+2sin2β=1,3sin2α﹣2sin2β=0,则α+2β值为 .
【解答】解:∵3sin2α+2sin2β=1,∴3sin2α=1﹣2sin2β=cos2β,
∵3sin2α﹣2sin2β=0,∴3sinαcosα=sin2β,
两式相除得:,
∴cosαcos2β﹣sinαsin2β=cos(α+2β)=0,
∵α,β均为锐角,
∴,
∴.
故答案为:.
14.(2025 海淀区校级模拟)如图,扇形OAB的半径为1,圆心角为,若P为弧AB上异于A,B的点,且PQ⊥OB交OB于Q点,当△POQ的面积大于时,设∠POQ=θ,满足上述条件的一个sinθ的取值为 (答案不唯一) .
【解答】解:由已知,OQ=cosθ,OP=1,所以△POQ的面积S,
由△POQ的面积大于,得,即sin2θ,
因为0<θ,所以解得2θ,θ,故sinθ,可取.
故答案为:(答案不唯一).
四.解答题(共5小题)
15.(2025春 内蒙古校级月考)函数的一个对称中心是.
(1)求函数f(x)的最值及x为何值时取到;
(2)用“五点法”画出函数f(x)在[0,π]上的简图.
【解答】解:(1)由题意得,
则,解得,
因为,所以k=1时,,
所以,其最大值为2,最小值为﹣2,
当,即时,函数f(x)取得最大值2;
当,即时,函数f(x)取得最小值﹣2.
(2)列表如下:
π 2π
x 0 π
y 2 0 ﹣2 0
函数f(x)在[0,π]上的简图如下,
16.(2025春 陕西月考)已知函数图象的相邻对称轴之间的距离为,且.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若对任意,都有2f(x)≥2c2﹣3c成立,求实数c的取值范围.
【解答】解:(1)函数图象的相邻对称轴之间的距离为,由函数f(x)图象的相邻对称轴之间的距离为,可得,
∴,可得ω=2,
又,可得,∵,
∴解得,
∴f(x)的解析式为.
(2)当时,,
∴,
∵对任意,都有2f(x)≥2c2﹣3c成立,
∴,即2c2﹣3c≤﹣1,解得.
∴实数c的取值范围为.
17.(2025 肇庆一模)已知向量,,ω>0,函数,且f(x)的最小正周期为π.
(1)若,求f(x)的值域;
(2)将f(x)的图象先向下平移个单位长度,再向左平移m(m>0)个单位长度,最后将横坐标变为原来的两倍,所得函数图象与函数y=cosx的图象重合,求实数m的最小值.
【解答】解:(1)向量,,ω>0,
则
,
因为f(x)最小正周期为π,所以,解得ω=1,
所以,
因为,所以,
则,
所以,
所以当时,f(x)的值域为.
(2)向下平移个单位长度得,
向左平移m(m>0)个单位长度得,
横坐标变为原来的2倍得.
因为,
所以要使得与y=cosx的图象重合,
则,k∈Z,解得,k∈Z
当k=0时,实数m取得最小值.
18.(2024秋 大兴区期末)如图,角α的顶点与原点O重合,始边与x轴的非负半轴重合,终边与单位圆O交于点P,且P的横坐标为,P在第二象限.
(Ⅰ)求sinα,tanα的值;
(Ⅱ)求的值.
【解答】解:(Ⅰ)因为P的横坐标为,P在第二象限,
所以P的纵坐标为,即P(,),
所以sinα,tanα2.
(Ⅱ)3+2.
19.(2025春 和平区校级月考)已知f(x)
(1)求f(x)的解析式.
(2)若,求tanx的值.
(3)若函数,如图A,B是直线y与曲线y=g(x)的两个交点,若|AB|,求g(x)的单调递减区间.
【解答】解:(1)依题意,,
由sinxcosx≠0得,k∈Z,
所以f(x)的解析式为.
(2)由(1)及,得,则,
两边平方得4sin2x+4sinxcosx+cos2x=5﹣5sin2x+5cos2x,
整理得(sinx﹣2cosx)2=0,因此sinx=2cosx,所以tanx=2.
(3)由,得,,k1,k∈Z,
由,得,因此,解得ω=2,,
由,k∈Z,解得,k∈Z,
所以g(x)的单调递减区间为,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
