2.2 圆的对称性 分层练习(含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 2.2 圆的对称性 分层练习(含答案) 2025-2026学年数学苏科版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 235.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 00:00:00 | ||
图片预览


文档简介
2.2 圆的对称性
第1课时 圆的旋转不变性
1.
下列说法中,正确的是 ( )
A. 相等的弦所对的弧相等
B. 在同圆或等圆中,相等的弧所对的圆心角相等
C. 在同圆或等圆中,较长的弧所对的弦较长
D. 相等的圆心角所对的弧相等
2. 在☉O中,弦AB的长等于圆的半径,则该弦所对的弧的度数为 ( )
A. 30° B. 60° C. 120° D. 以上都不对
3. (2024·苏州工业园区期中)如图,AB是☉O的直径,D、C是的三等分点.如果∠BOC=35°,那么∠AOE的度数为 .
4. 如图,在☉O中,AB、CD为弦,且AB=CD,则AC BD(填“>”“<”或“=”).
5. 已知☉O的一条弦AB把圆的周长分成1∶4的两部分,则弦AB所对的圆心角的度数为 .
6. 如图,正方形ABCD的四个顶点都在☉O上,M为的中点,连接BM、CM.求证:BM=CM.
第6题
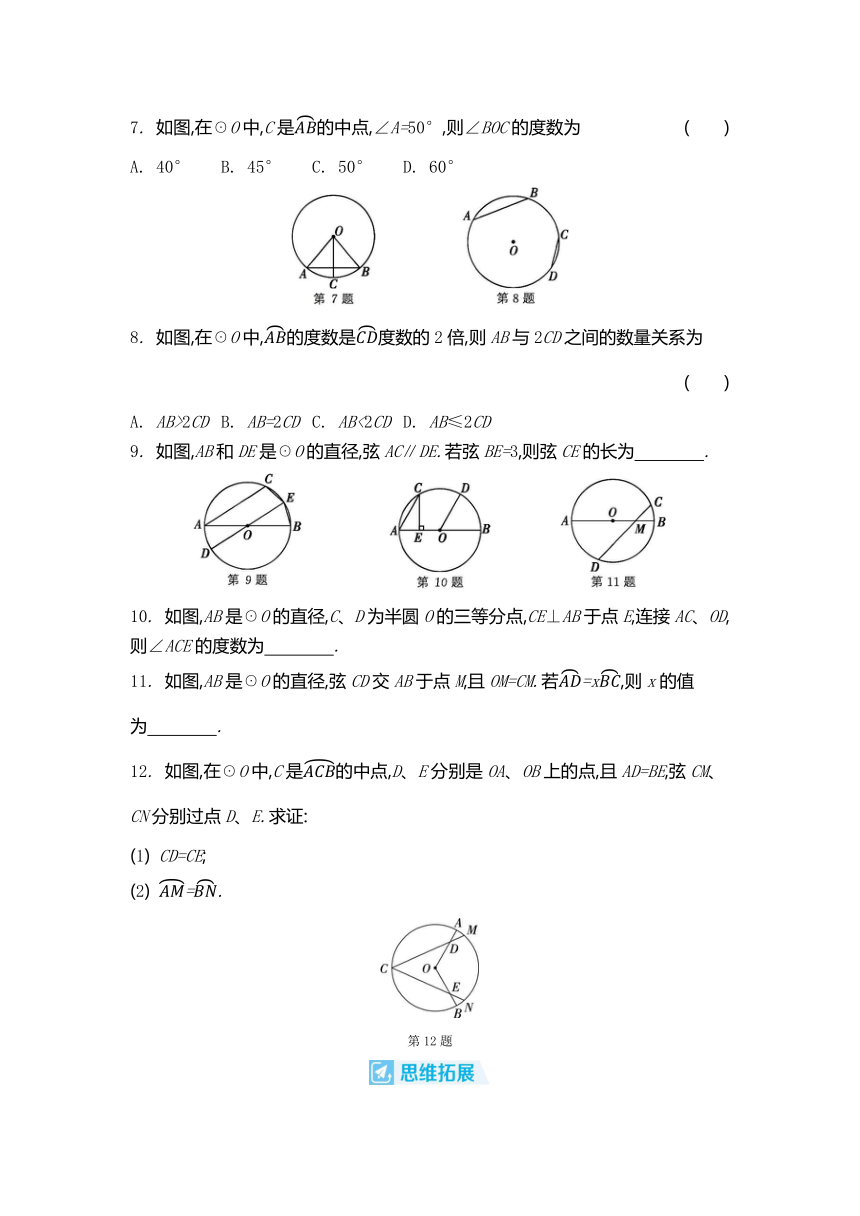
7. 如图,在☉O中,C是的中点,∠A=50°,则∠BOC的度数为 ( )
A. 40° B. 45° C. 50° D. 60°
8. 如图,在☉O中,的度数是度数的2倍,则AB与2CD之间的数量关系为 ( )
A. AB>2CD B. AB=2CD C. AB<2CD D. AB≤2CD
9. 如图,AB和DE是☉O的直径,弦AC∥DE.若弦BE=3,则弦CE的长为 .
10. 如图,AB是☉O的直径,C、D为半圆O的三等分点,CE⊥AB于点E,连接AC、OD,则∠ACE的度数为 .
11. 如图,AB是☉O的直径,弦CD交AB于点M,且OM=CM.若=x,则x的值为 .
12. 如图,在☉O中,C是的中点,D、E分别是OA、OB上的点,且AD=BE,弦CM、CN分别过点D、E.求证:
(1) CD=CE;
(2) =.
第12题
13. 如图,AB、DE为☉O的直径,C是☉O上一点,且=,连接BE、CE、AC、AD.
(1) BE与CE之间有什么数量关系 为什么
(2) 若∠BOE=60°,则四边形OACE是什么特殊四边形 请说明理由.
第13题
第2课时 圆的轴对称性
1.
(2023·潍坊改编)下列说法正确的是 ( )
A. 弦的垂线平分弦所对的弧 B. 平分弦的直径垂直于这条弦
C. 过弦中点的直线必过圆心 D. 弦所对的两条弧的中点的连线垂直平分弦
2. (2024·新疆)如图,AB是☉O的直径,CD是☉O的弦,AB⊥CD,垂足为E.若CD=8,OD=5,则BE的长为 ( )
A. 1 B. 2 C. 3 D. 4
3. 如图,在☉O中,弦AB的长为4,圆心到弦AB的距离为2,则∠AOC的度数为 .
4. (2024·苏州工业园区期中)如图,☉O的直径CD=10cm,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB= cm.
5. 如图,AC是☉O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F.若BD=8cm,AE=2cm,求☉O的半径及OF的长.
第5题
第6题
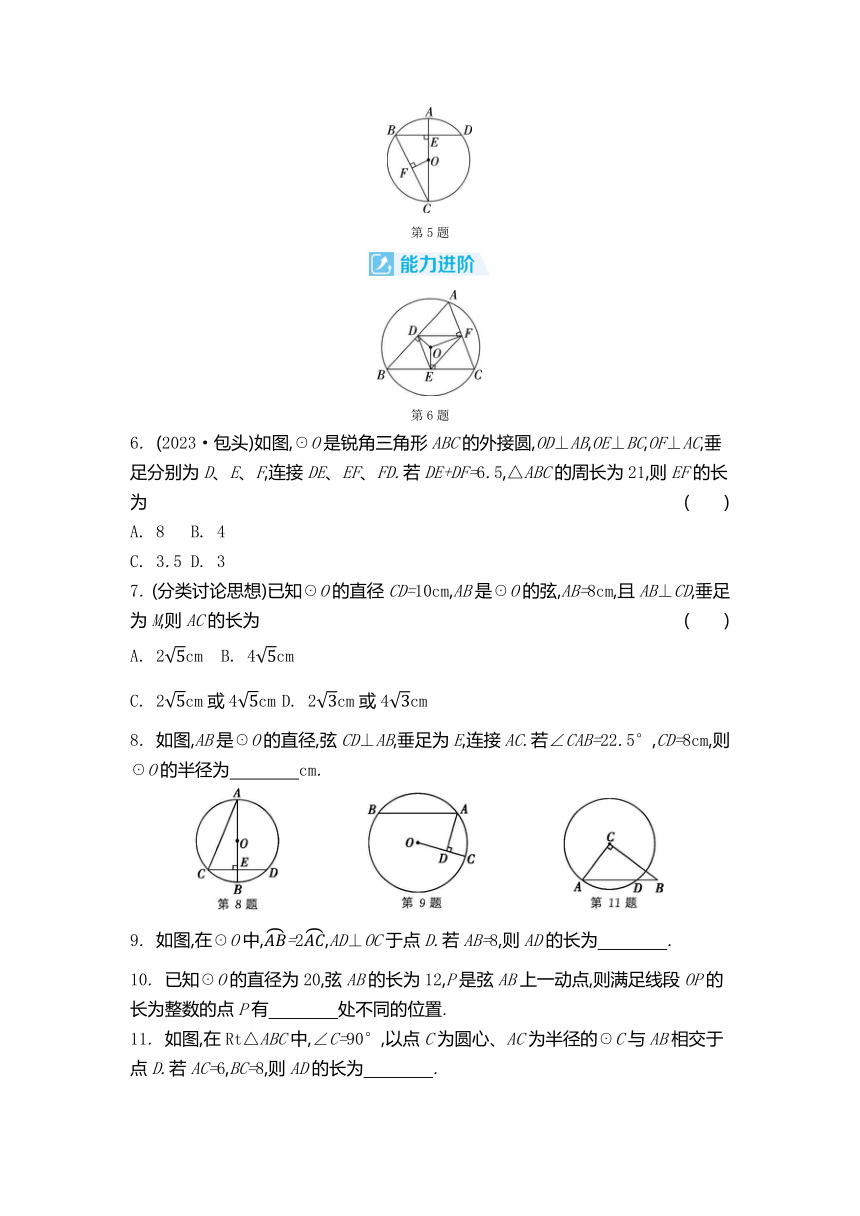
6. (2023·包头)如图,☉O是锐角三角形ABC的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D、E、F,连接DE、EF、FD.若DE+DF=6.5,△ABC的周长为21,则EF的长为 ( )
A. 8 B. 4
C. 3.5 D. 3
7. (分类讨论思想)已知☉O的直径CD=10cm,AB是☉O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为 ( )
A. 2cm B. 4cm
C. 2cm或4cm D. 2cm或4cm
8. 如图,AB是☉O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=8cm,则☉O的半径为 cm.
9. 如图,在☉O中,=2,AD⊥OC于点D.若AB=8,则AD的长为 .
10. 已知☉O的直径为20,弦AB的长为12,P是弦AB上一动点,则满足线段OP的长为整数的点P有 处不同的位置.
11. 如图,在Rt△ABC中,∠C=90°,以点C为圆心、AC为半径的☉C与AB相交于点D.若AC=6,BC=8,则AD的长为 .
12. (新情境·现实生活)(2023·广西改编)如图,某地有一座圆弧形拱桥,桥拱所在圆的圆心为点O,桥下水面的宽度AB为7.2m,过点O作OC⊥AB于点D,交圆弧于点C,CD=2.4m.现有一艘宽3m、船舱顶部高出水面AB2m的货船要经过这座拱桥,此货船能否顺利通过这座拱桥
第12题
13. (2024·包头)如图,AB是☉O的直径,BC、BD是☉O的两条弦,点C与点D在AB的两侧,E是OB上一点(OE>BE),连接OC、CE.若∠BOC=2∠BCE,且BD=2OE.求证:BD∥OC.
第13题
2.2 圆的对称性
第1课时 圆的旋转不变性
1. B 2. D 3. 75° 4. = 5. 72°
6. ∵ 四边形ABCD是正方形,∴ AB=CD,∴ =.∵ M为的中点,∴ =,∴ +=+,即=,∴ BM=CM
7. A 8. C 9. 3 10. 30°
11. 3 解析:连接OC、OD.∵ OC=OD,∴ ∠ODC=∠OCD.∵ OM=CM,∴ ∠OCD=∠BOC,∴ ∠ODC=∠BOC,∴ ∠OMD=∠OCD+∠BOC=2∠BOC,∴ ∠AOD= ∠OMD+∠ODC=3∠BOC,∴ =3,即x=3.
12. (1) 如图,连接OC.∵ C是的中点,∴ =,∴ ∠COD=∠COE.∵ OA=OB,AD=BE,∴ OD=OE.又∵ OC=OC,∴ △COD≌△COE,∴ CD=CE (2) 如图,连接OM、ON.∵ △COD≌△COE,∴ ∠CDO=∠CEO,∠OCD=∠OCE.∵ OC=OM=ON,∴ ∠OCM=∠M,∠OCN=∠N,∴ ∠M=∠N.∵ ∠CDO=∠M+∠MOD,∠CEO=∠N+∠NOE,∴ ∠MOD=∠NOE,∴ =
13. (1) BE=CE ∵ ∠BOE=∠AOD,∴ =.∵ =,∴ =,∴ BE=CE (2) 四边形OACE是菱形 理由:如图,连接OC.∵ BE=CE,∴ ∠BOE=∠COE=60°.又∵ OE=OC,∴ △OCE为等边三角形,∴ CE=OE.∵ ∠BOE+∠COE+∠AOC=180°,∴ ∠AOC=∠COE=60°,∴ AC=CE,∴ OE=CE=AC=OA,∴ 四边形OACE是菱形.
第2课时 圆的轴对称性
1. D 2. B 3. 45° 4. 8
5. 连接OB.∵ AC是☉O的直径,弦BD⊥AO于点E,BD=8cm,∴ BE=BD=4cm.设☉O的半径为xcm,则OB=OA=xcm,OE=(x-2)cm.在Rt△OEB中,由勾股定理,得OE2+BE2=OB2,即(x-2)2+42=x2,解得x=5.∴ ☉O的半径为5cm,∴ EC=2×5-2=8(cm),∴ 在Rt△BEC中,BC===4(cm).∵ OF⊥BC,OF过圆心,∴ CF=BC=2cm,∴ 在Rt△OFC中,OF===(cm)
6. B 7. C 8. 4 9. 4 10. 5
11. 解析:如图,连接CD,过点C作CH⊥AB于点H,则AH=AD.在Rt△ABC中,由勾股定理,得AB===10.由S△ABC=AC·BC=AB·CH,即×6×8=×10·CH,得CH=.在Rt△AHC中,由勾股定理,得AH===.∴ AD=2AH=.
12. 如图,连接ON、OB.∵ OC⊥AB,∴ D为AB的中点.∵ AB=7.2m,∴ BD=AB=3.6m.设OB=OC=ON=rm,则OD=(r-2.4)m.在Rt△BOD中,根据勾股定理,得OB2=OD2+BD2,即r2=(r-2.4)2+3.62,解得r=3.9.∵ CD=2.4m,船舱顶部高出水面AB 2m,∴ CE=2.4-2=0.4(m),∴ OE=3.9-0.4=3.5(m).易知OC⊥MN,∴ MN=2EN.在Rt△OEN中,EN===(m).∴ MN=2EN=2×≈3.44(m).∵ 3.44>3,∴ 此货船能顺利通过这座拱桥
13. 如图,过点O分别作OH⊥BC、OK⊥BD,垂足依次为H、K.∵ OK⊥BD,OK经过圆心,∴ ∠OKB=90°,BD=2BK.∵ BD=2OE,∴ OE=BK.∵ OB=OC,OH⊥BC,∴ ∠BOC=2∠BOH,∠OHB=90°,∴ 在Rt△OHB中,∠BOH+∠OBH=90°.∵ ∠BOC=2∠BCE,∴ ∠BOH=∠BCE,∴ ∠BCE+∠OBH=90°,∴ ∠OEC=∠BCE+∠OBH=90°.在Rt△OEC和Rt△BKO中,∴ Rt△OEC≌Rt△BKO,∴ ∠COE=∠OBK,∴ BD∥OC
第1课时 圆的旋转不变性
1.
下列说法中,正确的是 ( )
A. 相等的弦所对的弧相等
B. 在同圆或等圆中,相等的弧所对的圆心角相等
C. 在同圆或等圆中,较长的弧所对的弦较长
D. 相等的圆心角所对的弧相等
2. 在☉O中,弦AB的长等于圆的半径,则该弦所对的弧的度数为 ( )
A. 30° B. 60° C. 120° D. 以上都不对
3. (2024·苏州工业园区期中)如图,AB是☉O的直径,D、C是的三等分点.如果∠BOC=35°,那么∠AOE的度数为 .
4. 如图,在☉O中,AB、CD为弦,且AB=CD,则AC BD(填“>”“<”或“=”).
5. 已知☉O的一条弦AB把圆的周长分成1∶4的两部分,则弦AB所对的圆心角的度数为 .
6. 如图,正方形ABCD的四个顶点都在☉O上,M为的中点,连接BM、CM.求证:BM=CM.
第6题
7. 如图,在☉O中,C是的中点,∠A=50°,则∠BOC的度数为 ( )
A. 40° B. 45° C. 50° D. 60°
8. 如图,在☉O中,的度数是度数的2倍,则AB与2CD之间的数量关系为 ( )
A. AB>2CD B. AB=2CD C. AB<2CD D. AB≤2CD
9. 如图,AB和DE是☉O的直径,弦AC∥DE.若弦BE=3,则弦CE的长为 .
10. 如图,AB是☉O的直径,C、D为半圆O的三等分点,CE⊥AB于点E,连接AC、OD,则∠ACE的度数为 .
11. 如图,AB是☉O的直径,弦CD交AB于点M,且OM=CM.若=x,则x的值为 .
12. 如图,在☉O中,C是的中点,D、E分别是OA、OB上的点,且AD=BE,弦CM、CN分别过点D、E.求证:
(1) CD=CE;
(2) =.
第12题
13. 如图,AB、DE为☉O的直径,C是☉O上一点,且=,连接BE、CE、AC、AD.
(1) BE与CE之间有什么数量关系 为什么
(2) 若∠BOE=60°,则四边形OACE是什么特殊四边形 请说明理由.
第13题
第2课时 圆的轴对称性
1.
(2023·潍坊改编)下列说法正确的是 ( )
A. 弦的垂线平分弦所对的弧 B. 平分弦的直径垂直于这条弦
C. 过弦中点的直线必过圆心 D. 弦所对的两条弧的中点的连线垂直平分弦
2. (2024·新疆)如图,AB是☉O的直径,CD是☉O的弦,AB⊥CD,垂足为E.若CD=8,OD=5,则BE的长为 ( )
A. 1 B. 2 C. 3 D. 4
3. 如图,在☉O中,弦AB的长为4,圆心到弦AB的距离为2,则∠AOC的度数为 .
4. (2024·苏州工业园区期中)如图,☉O的直径CD=10cm,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB= cm.
5. 如图,AC是☉O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F.若BD=8cm,AE=2cm,求☉O的半径及OF的长.
第5题
第6题
6. (2023·包头)如图,☉O是锐角三角形ABC的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D、E、F,连接DE、EF、FD.若DE+DF=6.5,△ABC的周长为21,则EF的长为 ( )
A. 8 B. 4
C. 3.5 D. 3
7. (分类讨论思想)已知☉O的直径CD=10cm,AB是☉O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为 ( )
A. 2cm B. 4cm
C. 2cm或4cm D. 2cm或4cm
8. 如图,AB是☉O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=8cm,则☉O的半径为 cm.
9. 如图,在☉O中,=2,AD⊥OC于点D.若AB=8,则AD的长为 .
10. 已知☉O的直径为20,弦AB的长为12,P是弦AB上一动点,则满足线段OP的长为整数的点P有 处不同的位置.
11. 如图,在Rt△ABC中,∠C=90°,以点C为圆心、AC为半径的☉C与AB相交于点D.若AC=6,BC=8,则AD的长为 .
12. (新情境·现实生活)(2023·广西改编)如图,某地有一座圆弧形拱桥,桥拱所在圆的圆心为点O,桥下水面的宽度AB为7.2m,过点O作OC⊥AB于点D,交圆弧于点C,CD=2.4m.现有一艘宽3m、船舱顶部高出水面AB2m的货船要经过这座拱桥,此货船能否顺利通过这座拱桥
第12题
13. (2024·包头)如图,AB是☉O的直径,BC、BD是☉O的两条弦,点C与点D在AB的两侧,E是OB上一点(OE>BE),连接OC、CE.若∠BOC=2∠BCE,且BD=2OE.求证:BD∥OC.
第13题
2.2 圆的对称性
第1课时 圆的旋转不变性
1. B 2. D 3. 75° 4. = 5. 72°
6. ∵ 四边形ABCD是正方形,∴ AB=CD,∴ =.∵ M为的中点,∴ =,∴ +=+,即=,∴ BM=CM
7. A 8. C 9. 3 10. 30°
11. 3 解析:连接OC、OD.∵ OC=OD,∴ ∠ODC=∠OCD.∵ OM=CM,∴ ∠OCD=∠BOC,∴ ∠ODC=∠BOC,∴ ∠OMD=∠OCD+∠BOC=2∠BOC,∴ ∠AOD= ∠OMD+∠ODC=3∠BOC,∴ =3,即x=3.
12. (1) 如图,连接OC.∵ C是的中点,∴ =,∴ ∠COD=∠COE.∵ OA=OB,AD=BE,∴ OD=OE.又∵ OC=OC,∴ △COD≌△COE,∴ CD=CE (2) 如图,连接OM、ON.∵ △COD≌△COE,∴ ∠CDO=∠CEO,∠OCD=∠OCE.∵ OC=OM=ON,∴ ∠OCM=∠M,∠OCN=∠N,∴ ∠M=∠N.∵ ∠CDO=∠M+∠MOD,∠CEO=∠N+∠NOE,∴ ∠MOD=∠NOE,∴ =
13. (1) BE=CE ∵ ∠BOE=∠AOD,∴ =.∵ =,∴ =,∴ BE=CE (2) 四边形OACE是菱形 理由:如图,连接OC.∵ BE=CE,∴ ∠BOE=∠COE=60°.又∵ OE=OC,∴ △OCE为等边三角形,∴ CE=OE.∵ ∠BOE+∠COE+∠AOC=180°,∴ ∠AOC=∠COE=60°,∴ AC=CE,∴ OE=CE=AC=OA,∴ 四边形OACE是菱形.
第2课时 圆的轴对称性
1. D 2. B 3. 45° 4. 8
5. 连接OB.∵ AC是☉O的直径,弦BD⊥AO于点E,BD=8cm,∴ BE=BD=4cm.设☉O的半径为xcm,则OB=OA=xcm,OE=(x-2)cm.在Rt△OEB中,由勾股定理,得OE2+BE2=OB2,即(x-2)2+42=x2,解得x=5.∴ ☉O的半径为5cm,∴ EC=2×5-2=8(cm),∴ 在Rt△BEC中,BC===4(cm).∵ OF⊥BC,OF过圆心,∴ CF=BC=2cm,∴ 在Rt△OFC中,OF===(cm)
6. B 7. C 8. 4 9. 4 10. 5
11. 解析:如图,连接CD,过点C作CH⊥AB于点H,则AH=AD.在Rt△ABC中,由勾股定理,得AB===10.由S△ABC=AC·BC=AB·CH,即×6×8=×10·CH,得CH=.在Rt△AHC中,由勾股定理,得AH===.∴ AD=2AH=.
12. 如图,连接ON、OB.∵ OC⊥AB,∴ D为AB的中点.∵ AB=7.2m,∴ BD=AB=3.6m.设OB=OC=ON=rm,则OD=(r-2.4)m.在Rt△BOD中,根据勾股定理,得OB2=OD2+BD2,即r2=(r-2.4)2+3.62,解得r=3.9.∵ CD=2.4m,船舱顶部高出水面AB 2m,∴ CE=2.4-2=0.4(m),∴ OE=3.9-0.4=3.5(m).易知OC⊥MN,∴ MN=2EN.在Rt△OEN中,EN===(m).∴ MN=2EN=2×≈3.44(m).∵ 3.44>3,∴ 此货船能顺利通过这座拱桥
13. 如图,过点O分别作OH⊥BC、OK⊥BD,垂足依次为H、K.∵ OK⊥BD,OK经过圆心,∴ ∠OKB=90°,BD=2BK.∵ BD=2OE,∴ OE=BK.∵ OB=OC,OH⊥BC,∴ ∠BOC=2∠BOH,∠OHB=90°,∴ 在Rt△OHB中,∠BOH+∠OBH=90°.∵ ∠BOC=2∠BCE,∴ ∠BOH=∠BCE,∴ ∠BCE+∠OBH=90°,∴ ∠OEC=∠BCE+∠OBH=90°.在Rt△OEC和Rt△BKO中,∴ Rt△OEC≌Rt△BKO,∴ ∠COE=∠OBK,∴ BD∥OC
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
