2.2 圆的对称性 同步练(含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 2.2 圆的对称性 同步练(含答案) 2025-2026学年数学苏科版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 93.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 00:00:00 | ||
图片预览

文档简介
2.2 圆的对称性
第1课时 圆的旋转不变性
1. 圆是中心对称图形, 是它的对称中心.
2. (1) 在同圆或等圆中,相等的圆心角所对的弧 ,所对的弦 ;
(2) 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有 组量相等,那么它们所对应的其余各组量都分别 .
3. 圆心角的度数与它所对的弧的度数 .
1.
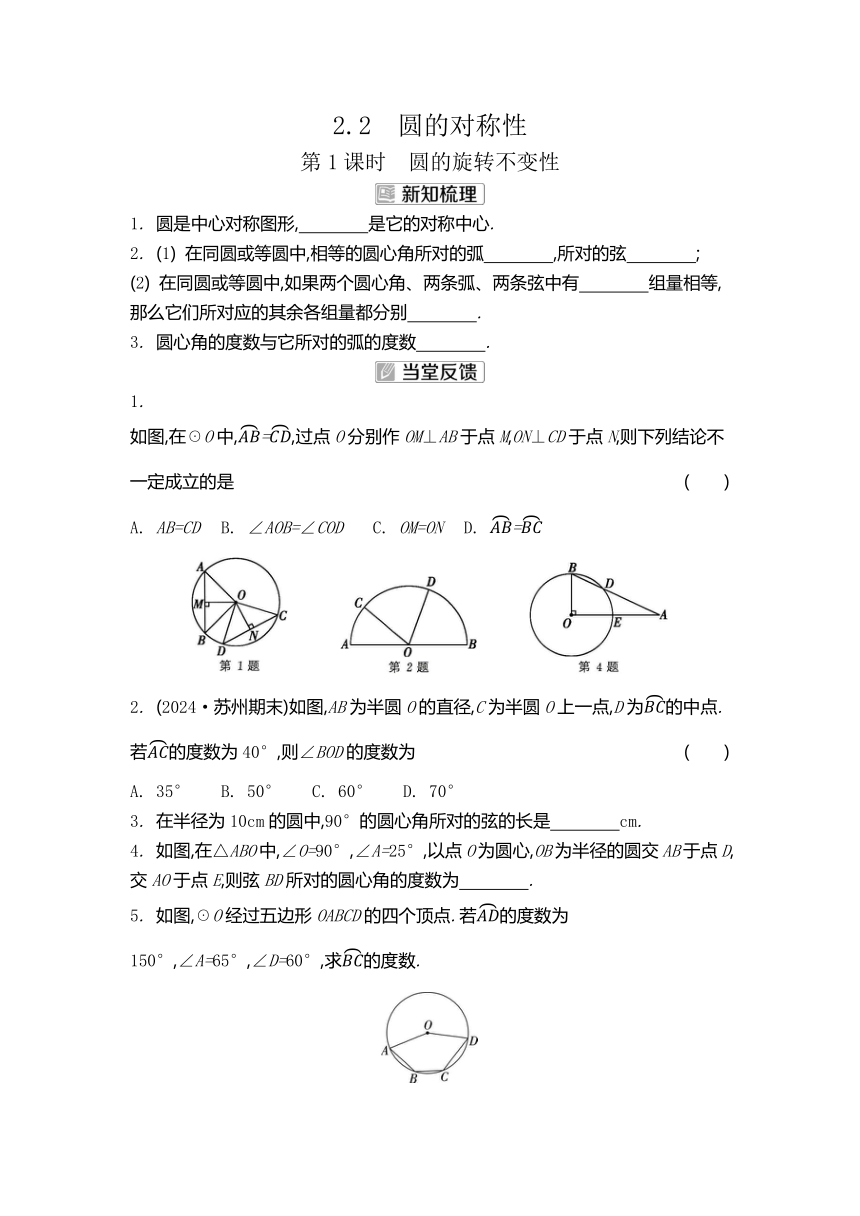
如图,在☉O中,=,过点O分别作OM⊥AB于点M,ON⊥CD于点N,则下列结论不一定成立的是 ( )
A. AB=CD B. ∠AOB=∠COD C. OM=ON D. =
2. (2024·苏州期末)如图,AB为半圆O的直径,C为半圆O上一点,D为的中点.若的度数为40°,则∠BOD的度数为 ( )
A. 35° B. 50° C. 60° D. 70°
3. 在半径为10cm的圆中,90°的圆心角所对的弦的长是 cm.
4. 如图,在△ABO中,∠O=90°,∠A=25°,以点O为圆心,OB为半径的圆交AB于点D,交AO于点E,则弦BD所对的圆心角的度数为 .
5. 如图,☉O经过五边形OABCD的四个顶点.若的度数为150°,∠A=65°,∠D=60°,求的度数.
第5题
第2课时 圆的轴对称性
1. 圆是轴对称图形, 都是它的对称轴.
2. 垂径定理:垂直于弦的直径平分 以及弦所对的 .
1.
如图,AB是☉O的弦,直径MN⊥AB,垂足为C,则下列结论不一定成立的是 ( )
A. AC=BC B. = C. = D. OC=CN
2. 已知☉O的半径为7,AB是☉O的弦,点P在弦AB上.若PA=4,PB=6,则OP的长为 ( )
A. B. 4 C. D. 5
3. (2024·长沙)如图,在☉O中,弦AB的长为8,圆心O到AB的距离OE=4,则☉O的半径为 .
4. (新情境·现实生活)(2023·永州)如图,☉O是一个盛有水的容器的横截面,☉O的半径为10cm,水的最深处到水面AB的距离为4cm,则水面AB的宽度为 cm.
5. (2024·遂宁改编)如图,AB是☉O的直径,AC是☉O的弦,D是的中点,DE⊥AB于点E,交AC于点F,交☉O于点H,DB交AC于点G,连接AD.
(1) 求证:AF=DF;
(2) 若AF=,=,求AE的长.
第5题
2.2 圆的对称性
第1课时 圆的旋转不变性
1. 圆心 2. (1) 相等 相等 (2) 一 相等 3. 相等
1. D 2. D 3. 10 4. 50°
5. 如图,连接OB、OC.∵ OA=OB,OC=OD,∴ △OAB、△OCD均为等腰三角形,∴ ∠A=∠ABO,∠OCD=∠D.∵ ∠A=65°,∠D=60°,∴ ∠AOB=180°-2∠A=50°,∠COD=180°-2∠D=60°.∵ 的度数为150°,∴ ∠AOD=150°,∴ ∠BOC=∠AOD-∠AOB-∠COD=150°-50°-60°=40°,∴ 的度数为40°
第2课时 圆的轴对称性
1. 过圆心的任意一条直线 2. 弦 两条弧
1. D 2. D 3. 4 4. 16
5. (1) ∵ D是的中点,∴ =.∵ AB⊥DH,且AB是☉O的直径,∴ =,∴ =,∴ ∠ADH=∠CAD,∴ AF=DF (2) 设AE=x,则AD=5x.∵ DE⊥AB,∴ ∠AED=90°,∴ 在Rt△AED中,DE==2x.∵ AF=,AF=DF,∴ DF=.∵ 在Rt△AEF中,AE2+EF2=AF2,∴ (x)2+=,解得x=(x=0舍去),∴ AE=x=2
第1课时 圆的旋转不变性
1. 圆是中心对称图形, 是它的对称中心.
2. (1) 在同圆或等圆中,相等的圆心角所对的弧 ,所对的弦 ;
(2) 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有 组量相等,那么它们所对应的其余各组量都分别 .
3. 圆心角的度数与它所对的弧的度数 .
1.
如图,在☉O中,=,过点O分别作OM⊥AB于点M,ON⊥CD于点N,则下列结论不一定成立的是 ( )
A. AB=CD B. ∠AOB=∠COD C. OM=ON D. =
2. (2024·苏州期末)如图,AB为半圆O的直径,C为半圆O上一点,D为的中点.若的度数为40°,则∠BOD的度数为 ( )
A. 35° B. 50° C. 60° D. 70°
3. 在半径为10cm的圆中,90°的圆心角所对的弦的长是 cm.
4. 如图,在△ABO中,∠O=90°,∠A=25°,以点O为圆心,OB为半径的圆交AB于点D,交AO于点E,则弦BD所对的圆心角的度数为 .
5. 如图,☉O经过五边形OABCD的四个顶点.若的度数为150°,∠A=65°,∠D=60°,求的度数.
第5题
第2课时 圆的轴对称性
1. 圆是轴对称图形, 都是它的对称轴.
2. 垂径定理:垂直于弦的直径平分 以及弦所对的 .
1.
如图,AB是☉O的弦,直径MN⊥AB,垂足为C,则下列结论不一定成立的是 ( )
A. AC=BC B. = C. = D. OC=CN
2. 已知☉O的半径为7,AB是☉O的弦,点P在弦AB上.若PA=4,PB=6,则OP的长为 ( )
A. B. 4 C. D. 5
3. (2024·长沙)如图,在☉O中,弦AB的长为8,圆心O到AB的距离OE=4,则☉O的半径为 .
4. (新情境·现实生活)(2023·永州)如图,☉O是一个盛有水的容器的横截面,☉O的半径为10cm,水的最深处到水面AB的距离为4cm,则水面AB的宽度为 cm.
5. (2024·遂宁改编)如图,AB是☉O的直径,AC是☉O的弦,D是的中点,DE⊥AB于点E,交AC于点F,交☉O于点H,DB交AC于点G,连接AD.
(1) 求证:AF=DF;
(2) 若AF=,=,求AE的长.
第5题
2.2 圆的对称性
第1课时 圆的旋转不变性
1. 圆心 2. (1) 相等 相等 (2) 一 相等 3. 相等
1. D 2. D 3. 10 4. 50°
5. 如图,连接OB、OC.∵ OA=OB,OC=OD,∴ △OAB、△OCD均为等腰三角形,∴ ∠A=∠ABO,∠OCD=∠D.∵ ∠A=65°,∠D=60°,∴ ∠AOB=180°-2∠A=50°,∠COD=180°-2∠D=60°.∵ 的度数为150°,∴ ∠AOD=150°,∴ ∠BOC=∠AOD-∠AOB-∠COD=150°-50°-60°=40°,∴ 的度数为40°
第2课时 圆的轴对称性
1. 过圆心的任意一条直线 2. 弦 两条弧
1. D 2. D 3. 4 4. 16
5. (1) ∵ D是的中点,∴ =.∵ AB⊥DH,且AB是☉O的直径,∴ =,∴ =,∴ ∠ADH=∠CAD,∴ AF=DF (2) 设AE=x,则AD=5x.∵ DE⊥AB,∴ ∠AED=90°,∴ 在Rt△AED中,DE==2x.∵ AF=,AF=DF,∴ DF=.∵ 在Rt△AEF中,AE2+EF2=AF2,∴ (x)2+=,解得x=(x=0舍去),∴ AE=x=2
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
