2.4 圆周角 分层练习(含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 2.4 圆周角 分层练习(含答案) 2025-2026学年数学苏科版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 369.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 14:34:20 | ||
图片预览



文档简介
2.4 圆周角
第1课时 圆周角的概念与性质
1.
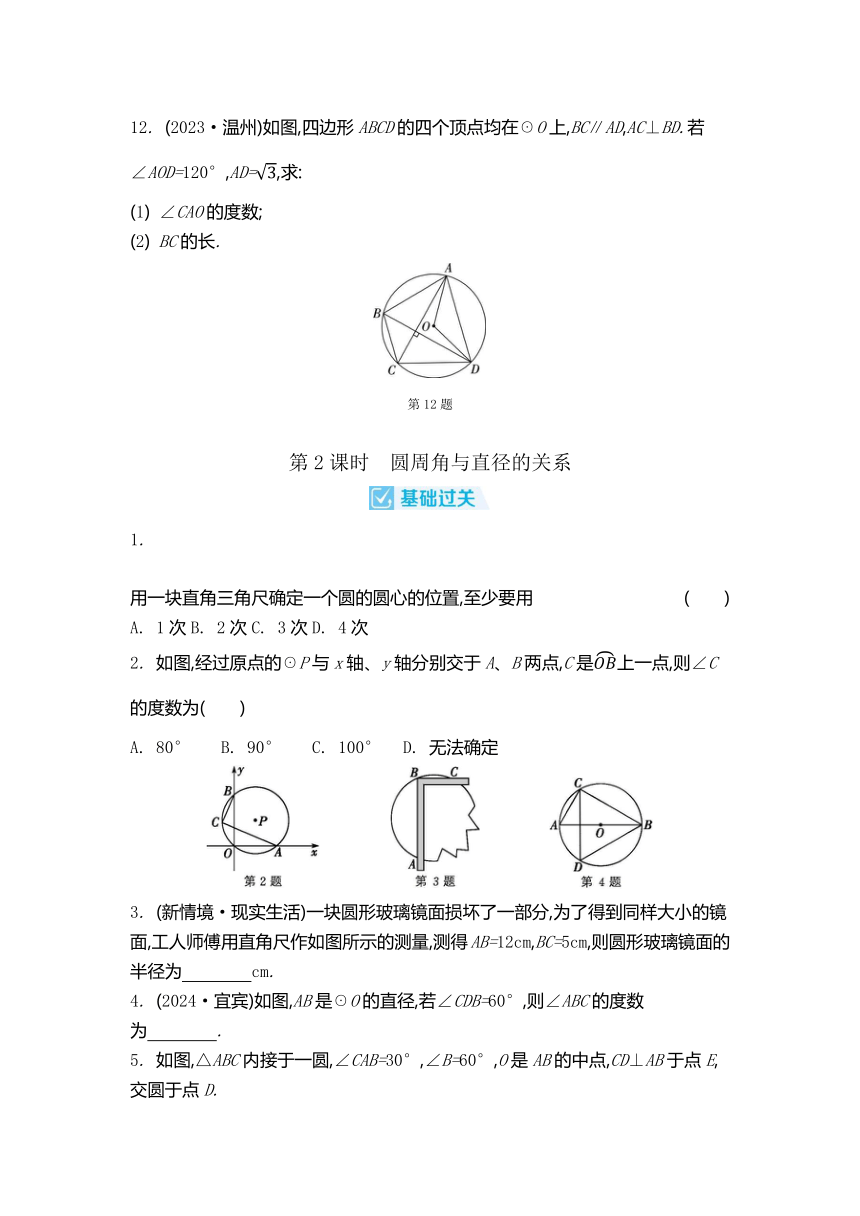
(2024·云南)如图,CD是☉O的直径,点A、B在☉O上.若=,∠AOC=36°,则∠D的度数为 ( )
A. 9° B. 18° C. 36° D. 45°
2. 如图,点O为所在圆的圆心,∠AOC=108°,点D在AB的延长线上,BD=BC,则∠D的度数为 ( )
A. 27° B. 30° C. 33° D. 54°
3. (2025·苏州期末)如图,☉O上有三点A、B、C,连接AB、AC、OB、OC.已知∠A=36°,则∠BOC的度数为 .
4. (2024·重庆B卷改编)如图,AB是☉O的弦,OC⊥AB交☉O于点C,D是☉O上一点,连接BD、CD.若∠D=28°,则∠OAB的度数为 .
5. (2024·哈尔滨)如图,在☉O中,弦AB、CD相交于点E,AE=CE,连接AC、BD.
(1) 求证:AC∥BD;
(2) 连接EO并延长,交BD于点F,求证:∠BEF=∠DEF.
第5题
第6题
6. (2024·海南)如图,AD是半圆O的直径,点B、C在半圆上,且==,点P在上.若∠PCB=130°,则∠PBA的度数为 ( )
A. 105° B. 100°
C. 90° D. 70°
7. (2024·昆山期末)如图,☉O是△ABC的外接圆,E是BC的中点,连接OE并延长,交☉O于点D,连接BD.若∠D=62°,则∠A的度数为 ( )
A. 56° B. 58° C. 60° D. 62°
8. (2024·菏泽)如图,△ABC是☉O的内接三角形.若OA∥CB,∠ACB=25°,则∠CAB= °.
9. 如图,AB、CD是☉O的弦,延长AB、CD相交于点P.若∠P=30°,∠AOC=80°,则的度数是 .
10. (转化与化归思想)(2023·鞍山)如图,AC、BC为☉O的两条弦,D、G分别为AC、BC的中点,☉O的半径为2.若∠C=45°,则DG的长为 .
11. 如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD,交△ABC的外接圆☉O于点E,连接AE.
(1) 求证:四边形AECD为平行四边形;
(2) 连接CO,求证:CO平分∠BCE.
第11题
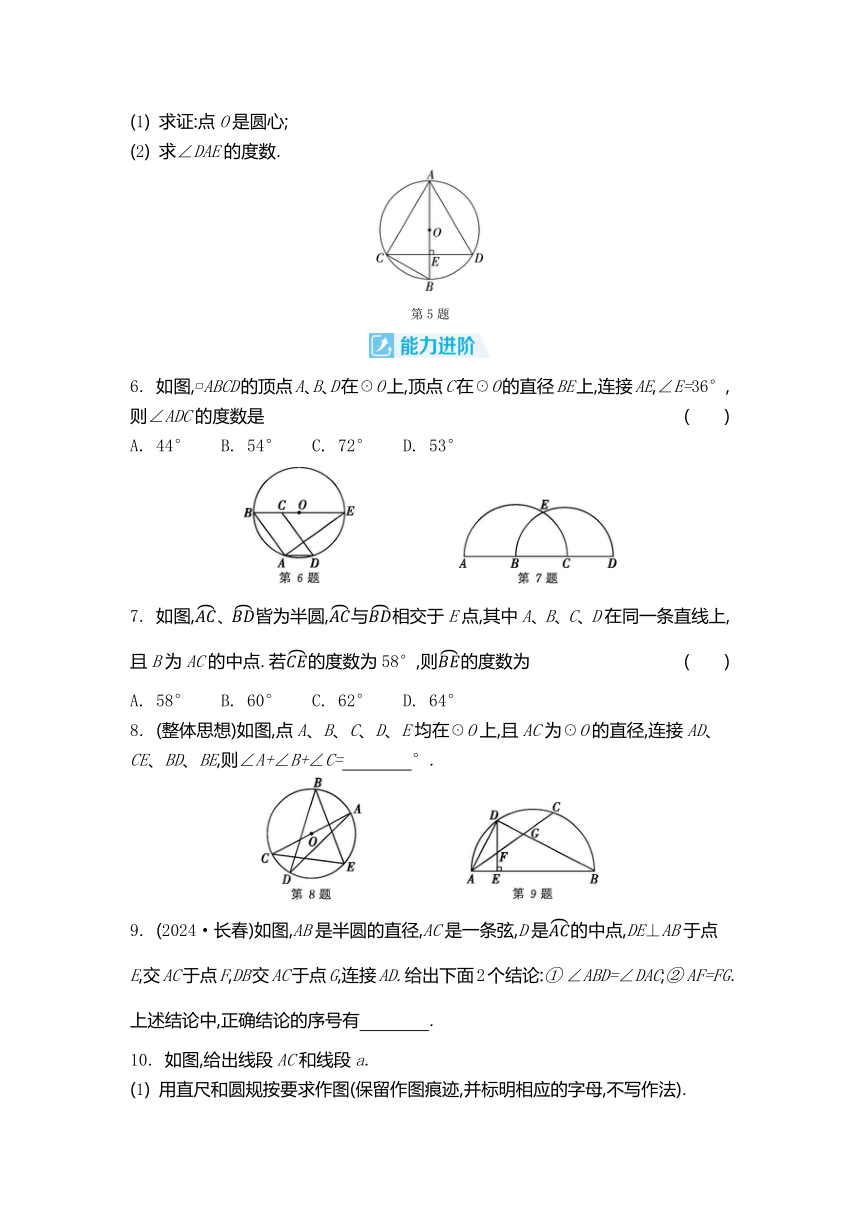
12. (2023·温州)如图,四边形ABCD的四个顶点均在☉O上,BC∥AD,AC⊥BD.若∠AOD=120°,AD=,求:
(1) ∠CAO的度数;
(2) BC的长.
第12题
第2课时 圆周角与直径的关系
1.
用一块直角三角尺确定一个圆的圆心的位置,至少要用 ( )
A. 1次 B. 2次 C. 3次 D. 4次
2. 如图,经过原点的☉P与x轴、y轴分别交于A、B两点,C是上一点,则∠C的度数为( )
A. 80° B. 90° C. 100° D. 无法确定
3. (新情境·现实生活)一块圆形玻璃镜面损坏了一部分,为了得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形玻璃镜面的半径为 cm.
4. (2024·宜宾)如图,AB是☉O的直径,若∠CDB=60°,则∠ABC的度数为 .
5. 如图,△ABC内接于一圆,∠CAB=30°,∠B=60°,O是AB的中点,CD⊥AB于点E,交圆于点D.
(1) 求证:点O是圆心;
(2) 求∠DAE的度数.
第5题
6. 如图, ABCD的顶点A、B、D在☉O上,顶点C在☉O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是 ( )
A. 44° B. 54° C. 72° D. 53°
7. 如图,、皆为半圆,与相交于E点,其中A、B、C、D在同一条直线上,且B为AC的中点.若的度数为58°,则的度数为 ( )
A. 58° B. 60° C. 62° D. 64°
8. (整体思想)如图,点A、B、C、D、E均在☉O上,且AC为☉O的直径,连接AD、CE、BD、BE,则∠A+∠B+∠C= °.
9. (2024·长春)如图,AB是半圆的直径,AC是一条弦,D是的中点,DE⊥AB于点E,交AC于点F,DB交AC于点G,连接AD.给出下面2个结论:① ∠ABD=∠DAC;② AF=FG.上述结论中,正确结论的序号有 .
10. 如图,给出线段AC和线段a.
(1) 用直尺和圆规按要求作图(保留作图痕迹,并标明相应的字母,不写作法).
① 作线段AC的垂直平分线l,交线段AC于点O;
② 以线段AC为对角线,作矩形ABCD,使得AB=a,且点B在线段AC的上方.
(2) 当AC=4,a=2时,(1)中所作矩形ABCD的面积为 .
11. (2024·安徽)如图,☉O是△ABC的外接圆,D是直径AB上一点,∠ACD的平分线交AB于点E,交☉O于另一点F,FA=FE.
(1) 求证:CD⊥AB;
(2) 若FM⊥AB,垂足为M,OM=OE=1,求AC的长.
第11题
第3课时 圆的内接四边形
1.
有下列命题:① 圆内接平行四边形是矩形;② 圆内接矩形是正方形;③ 圆内接菱形是正方形.其中,真命题是 ( )
A. ①② B. ①②③ C. ②③ D. ①③
2. (2024·吉林)如图,四边形ABCD内接于☉O,过点B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是 ( )
A. 50° B. 100° C. 130° D. 150°
3. 如图,四边形ABCD为☉O的内接四边形,∠C=∠D,则AB与CD之间的位置关系是
.
4. 如图,四边形ABCD是☉O的内接四边形,AD与BC的延长线交于点E,BA与CD的延长线交于点F,∠DCE=80°,∠F=25°,则∠E的度数为 .
5. 如图,☉O1和☉O2都经过A、B两点.经过点A的直线CD交☉O1于点C,交☉O2于点D;经过点B的直线EF交☉O1于点E,交☉O2于点F.试判断CE与DF是否平行,并说明理由.
第5题
6. 如图,点C、D在以AB为直径的半圆O上,且∠ADC=120°,E是上任意一点,连接BC、BE、CE,则∠BEC的度数为 ( )
A. 20° B. 30° C. 40° D. 60°
7. (2023·淮安)如图,四边形ABCD是☉O的内接四边形,BC是☉O的直径,BC=2CD,则∠BAD的度数为 .
8. (2024·巴中改编)如图,四边形ABCD是菱形,☉O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=80°,则∠EAC的度数为 .
9. 如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在y轴的正半轴上,☉D经过A、B、O、C四点,∠ACO=120°,AB=4,则圆心D的坐标是 .
10. 如图,四边形ABCD内接于☉O,AB=CD,A为的中点,连接BD,∠BDC=60°,则∠ADB的度数为 .
11. 如图,四边形ABCD内接于☉O,∠ABC=60°,对角线DB平分∠ADC.
(1) 求证:△ABC是等边三角形;
(2) 若AD=2,DC=3,求△ABC的周长.
第11题
12. (2023·北京)如图,圆内接四边形ABCD的对角线AC、BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
(1) 求证:DB平分∠ADC,并求∠BAD的度数.
(2) 过点C作CF∥AD,交AB的延长线于点F.若AC=AD,BF=2,求此圆的半径.
第12题
2.4 圆 周 角
第1课时 圆周角的概念与性质
1. B 2. A 3. 72° 4. 34°
5. (1) ∵ AE=CE,∴ ∠A=∠C.∵ =,∴ ∠C=∠EBD,∴ ∠A=∠EBD,∴ AC∥BD (2) 连接OD、OB.∵ =,∴ ∠EDB=∠A.由(1)知,∠EBD=∠C,∠A=∠C,∴ ∠EDB=∠EBD,∴ EB=ED.∵ OE=OE,OB=OD,∴ △BOE≌△DOE,∴ ∠BEF=∠DEF
6. B 7. A 8. 40 9. 20°
10. 解析:连接AO、BO、AB.根据圆周角定理,得∠AOB=2∠C=90°.在Rt△AOB中,根据勾股定理,可得AB=2.在△CAB中,根据三角形的中位线定理,可得DG=AB=.
11. (1) ∵ =,∴ ∠B=∠E.∵ ∠B=∠D,∴ ∠E=∠D.∵ CE∥AD,∴ ∠D+∠ECD=180°,∴ ∠E+∠ECD=180°,∴ AE∥CD,∴ 四边形AECD为平行四边形 (2) 如图,连接OE、OB.∵ 四边形AECD为平行四边形,∴ AD=EC.∵ AD=BC,∴ EC=BC.又∵ OC=OC,OE=OB,∴ △COE≌△COB,∴ ∠OCE=∠OCB,即CO平分∠BCE
12. (1) 如图,设AC、BD交于点E.∵ AC⊥BD,∴ ∠AED=90°.∵ BC∥AD,∴ ∠DBC=∠ADB.∵ =,∴ ∠DBC=∠DAC,∴ ∠ADB=∠DAC,∴ 在Rt△AED中,∠ADB=∠DAC=45°.∵ OA=OD,∴ ∠OAD=∠ODA.∵ 在△OAD中,∠AOD=120°,∴ ∠OAD=30°,∴ ∠CAO=∠DAC-∠OAD=15° (2) 如图,连接OB、OC,过点O作OH⊥AD,垂足为H.∵ OA=OD,OH⊥AD,∴ AH=AD=.∵ 在Rt△OHA中,∠OAH=30°,∴ 易得OH=OA.在Rt△OHA中,由勾股定理,得OH2+AH2=OA2,∴ +=OA2,解得OA=1(负值舍去).∵ =,∴ ∠COD=2∠DAC=90°.同理,得∠AOB=90°.∵ ∠AOD=120°,∴ ∠BOC=360°-90°-90°-120°=60°.∵ OB=OC,∴ △OBC是等边三角形,∴ BC=OB.∵ OB=OA=1,∴ BC=1
第2课时 圆周角与直径的关系
1. B 2. B 3. 4. 30°
5. (1) ∵ ∠CAB=30°,∠B=60°,∴ ∠ACB=180°-∠CAB-∠B=90°.又∵ A、B两点都在圆上,∴ AB是圆的直径.又∵ O是AB的中点,∴ 点O是圆心
(2) ∵ =,∴ ∠D=∠B=60°.∵ AB⊥CD,∴ ∠DAE=90°-∠D=30°
6. B
7. D 解析:如图,连接BE、DE.由题意,得AC是左边半圆的直径,BD是右边半圆的直径.∵ B为AC的中点,∴ 点B是左边半圆的圆心.∵ 的度数为58°,∴ ∠EBC=58°.∵ BD是右边半圆的直径,∴ ∠BED=90°,∴ 在Rt△BED中,∠EDB=90°-58°=32°,∴ 的度数为32°×2=64°.
8. 90
9. ①② 解析:∵ D是的中点,∴ =,∴ ∠ABD=∠DAC.故①正确.∵ AB是半圆的直径,∴ ∠ADB=90°,∴ 在Rt△ADB中,∠DAB+∠ABD=90°.∵ DE⊥AB,∴ 在Rt△AED中,∠DAB+∠ADE=90°,∴ ∠ABD=∠ADE,∴ ∠ADE=∠DAC,∴ AF=DF.∵ 在Rt△ADG中,∠DAC+∠AGD=90°,∠ADE+∠FDG=90°,∴ ∠AGD=∠FDG,∴ DF=FG,∴ AF=FG.综上所述,正确结论的序号有①②.
10. (1) ① 如图,直线l即为所求作
② 如图,矩形ABCD即为所求作 解析:以AC为直径作☉O,以点A为圆心,在AC上方截取AB=a,交☉O于点B;以点C为圆心,在AC下方截取CD=a,交☉O于点D,连接AB、BC、CD、AD.
(2) 4
11. (1) ∵ FA=FE,∴ ∠FAE=∠AEF.∵ =,∴ ∠FAE=∠BCE.∵ ∠AEF=∠CEB,∴ ∠CEB=∠BCE.∵ CE平分∠ACD,∴ ∠ACE=∠DCE.∵ AB是☉O的直径,∴ ∠ACB=90°,即∠BCE+∠ACE=90°,∴ ∠CEB+∠DCE=90°.∵ △CDE的内角和为180°,∴ ∠CDE=90°,∴ CD⊥AB (2) 由(1)知,∠BEC=∠BCE,∴ BE=BC.∵ OM=OE=1,∴ ME=OM+OE=2.∵ AF=EF,FM⊥AB,∴ MA=ME=2,∴ AE=4,∴ OA=OB=AE-OE=3,∴ BC=BE=OB-OE=2,AB=OA+OB=6,∴ 在Rt△ABC中,AC===4
第3课时 圆的内接四边形
1. D 2. C 3. AB∥CD 4. 45°
5. CE与DF平行 理由:连接AB.∵ 四边形ABEC是☉O1的内接四边形,∴ ∠BAC+∠BEC=180°.∵ ∠BAC+∠BAD=180°,∴ ∠BAD=∠BEC.∵ 四边形ABFD是☉O2的内接四边形,∴ ∠BAD+∠BFD=180°,∴ ∠BEC+∠BFD=180°,∴ CE∥DF.
6. B 7. 120° 8. 30° 9. (-,1)
10. 40° 解析:设∠ADB=x.∵ A为的中点,∴ =,∴ ∠ABD=∠ADB=x.∵ AB=CD,∴ =,∴ ∠CBD=∠ADB=x.∵ 四边形ABCD内接于☉O,∴ ∠ABC+∠ADC=180°.∵ ∠BDC=60°,∴ 3x+60°=180°,解得x=40°,即∠ADB=40°.
11. (1) ∵ 四边形ABCD内接于☉O,∴ ∠ABC+∠ADC=180°.∵ ∠ABC=60°,∴ ∠ADC=120°.∵ DB平分∠ADC,∴ ∠ADB=∠CDB=60°.∵ =,=,∴ ∠ACB=∠ADB=60°,∠BAC=∠CDB=60°,∴ ∠ABC=∠ACB=∠BAC,∴ △ABC是等边三角形 (2) 如图,过点A作AM⊥CD,交CD的延长线于点M.∴ ∠AMD=90°.∵ ∠ADC=120°,∴ ∠ADM=180°-∠ADC=60°,∴ 在Rt△AMD中,∠DAM=30°,∴ 易得DM=AD=1,∴ AM==.∵ CD=3,∴ CM=CD+DM=4,∴ 在Rt△AMC中, AC==.∵ △ABC是等边三角形,∴ AB=BC=AC=,∴ △ABC的周长为3
12. (1) ∵ =,∴ ∠BAC=∠CDB.∵ ∠BAC=∠ADB,∴ ∠CDB=∠ADB,即DB平分∠ADC.∵ BD平分∠ABC,∴ ∠ABD=∠CBD.∵ △ABD与△CBD的内角和均为180°,∴ ∠BAD=∠BCD.∵ 四边形ABCD是圆内接四边形,∴ ∠BAD+∠BCD=180°,∴ ∠BAD=∠BCD=90° (2) ∵ ∠BAD=90°,∴ BD是圆的直径.∵ ∠ABD=∠CBD,∴ =,∴ AD=CD.∵ AC=AD,∴ AC=AD=CD,∴ △ADC是等边三角形,∴ ∠ADC=60°,∴ ∠CDB=∠ADC=30°,∴ 在Rt△BCD中,易得BD=2BC.∵ CF∥AD,∴ ∠F+∠BAD=180°,∴ ∠F=90°.∵ 四边形ABCD是圆内接四边形,∴ ∠ADC+∠ABC=180°,∴ ∠ABC=120°,∴ ∠FBC=180°-∠ABC=60°,∴ ∠FCB=90°-60°=30°,∴ 在Rt△BFC中,易得BF=BC.∵ BF=2,∴ BC=4,∴ BD=8.∵ BD是圆的直径,∴ 该圆的半径为BD=4
第1课时 圆周角的概念与性质
1.
(2024·云南)如图,CD是☉O的直径,点A、B在☉O上.若=,∠AOC=36°,则∠D的度数为 ( )
A. 9° B. 18° C. 36° D. 45°
2. 如图,点O为所在圆的圆心,∠AOC=108°,点D在AB的延长线上,BD=BC,则∠D的度数为 ( )
A. 27° B. 30° C. 33° D. 54°
3. (2025·苏州期末)如图,☉O上有三点A、B、C,连接AB、AC、OB、OC.已知∠A=36°,则∠BOC的度数为 .
4. (2024·重庆B卷改编)如图,AB是☉O的弦,OC⊥AB交☉O于点C,D是☉O上一点,连接BD、CD.若∠D=28°,则∠OAB的度数为 .
5. (2024·哈尔滨)如图,在☉O中,弦AB、CD相交于点E,AE=CE,连接AC、BD.
(1) 求证:AC∥BD;
(2) 连接EO并延长,交BD于点F,求证:∠BEF=∠DEF.
第5题
第6题
6. (2024·海南)如图,AD是半圆O的直径,点B、C在半圆上,且==,点P在上.若∠PCB=130°,则∠PBA的度数为 ( )
A. 105° B. 100°
C. 90° D. 70°
7. (2024·昆山期末)如图,☉O是△ABC的外接圆,E是BC的中点,连接OE并延长,交☉O于点D,连接BD.若∠D=62°,则∠A的度数为 ( )
A. 56° B. 58° C. 60° D. 62°
8. (2024·菏泽)如图,△ABC是☉O的内接三角形.若OA∥CB,∠ACB=25°,则∠CAB= °.
9. 如图,AB、CD是☉O的弦,延长AB、CD相交于点P.若∠P=30°,∠AOC=80°,则的度数是 .
10. (转化与化归思想)(2023·鞍山)如图,AC、BC为☉O的两条弦,D、G分别为AC、BC的中点,☉O的半径为2.若∠C=45°,则DG的长为 .
11. 如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD,交△ABC的外接圆☉O于点E,连接AE.
(1) 求证:四边形AECD为平行四边形;
(2) 连接CO,求证:CO平分∠BCE.
第11题
12. (2023·温州)如图,四边形ABCD的四个顶点均在☉O上,BC∥AD,AC⊥BD.若∠AOD=120°,AD=,求:
(1) ∠CAO的度数;
(2) BC的长.
第12题
第2课时 圆周角与直径的关系
1.
用一块直角三角尺确定一个圆的圆心的位置,至少要用 ( )
A. 1次 B. 2次 C. 3次 D. 4次
2. 如图,经过原点的☉P与x轴、y轴分别交于A、B两点,C是上一点,则∠C的度数为( )
A. 80° B. 90° C. 100° D. 无法确定
3. (新情境·现实生活)一块圆形玻璃镜面损坏了一部分,为了得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形玻璃镜面的半径为 cm.
4. (2024·宜宾)如图,AB是☉O的直径,若∠CDB=60°,则∠ABC的度数为 .
5. 如图,△ABC内接于一圆,∠CAB=30°,∠B=60°,O是AB的中点,CD⊥AB于点E,交圆于点D.
(1) 求证:点O是圆心;
(2) 求∠DAE的度数.
第5题
6. 如图, ABCD的顶点A、B、D在☉O上,顶点C在☉O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是 ( )
A. 44° B. 54° C. 72° D. 53°
7. 如图,、皆为半圆,与相交于E点,其中A、B、C、D在同一条直线上,且B为AC的中点.若的度数为58°,则的度数为 ( )
A. 58° B. 60° C. 62° D. 64°
8. (整体思想)如图,点A、B、C、D、E均在☉O上,且AC为☉O的直径,连接AD、CE、BD、BE,则∠A+∠B+∠C= °.
9. (2024·长春)如图,AB是半圆的直径,AC是一条弦,D是的中点,DE⊥AB于点E,交AC于点F,DB交AC于点G,连接AD.给出下面2个结论:① ∠ABD=∠DAC;② AF=FG.上述结论中,正确结论的序号有 .
10. 如图,给出线段AC和线段a.
(1) 用直尺和圆规按要求作图(保留作图痕迹,并标明相应的字母,不写作法).
① 作线段AC的垂直平分线l,交线段AC于点O;
② 以线段AC为对角线,作矩形ABCD,使得AB=a,且点B在线段AC的上方.
(2) 当AC=4,a=2时,(1)中所作矩形ABCD的面积为 .
11. (2024·安徽)如图,☉O是△ABC的外接圆,D是直径AB上一点,∠ACD的平分线交AB于点E,交☉O于另一点F,FA=FE.
(1) 求证:CD⊥AB;
(2) 若FM⊥AB,垂足为M,OM=OE=1,求AC的长.
第11题
第3课时 圆的内接四边形
1.
有下列命题:① 圆内接平行四边形是矩形;② 圆内接矩形是正方形;③ 圆内接菱形是正方形.其中,真命题是 ( )
A. ①② B. ①②③ C. ②③ D. ①③
2. (2024·吉林)如图,四边形ABCD内接于☉O,过点B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是 ( )
A. 50° B. 100° C. 130° D. 150°
3. 如图,四边形ABCD为☉O的内接四边形,∠C=∠D,则AB与CD之间的位置关系是
.
4. 如图,四边形ABCD是☉O的内接四边形,AD与BC的延长线交于点E,BA与CD的延长线交于点F,∠DCE=80°,∠F=25°,则∠E的度数为 .
5. 如图,☉O1和☉O2都经过A、B两点.经过点A的直线CD交☉O1于点C,交☉O2于点D;经过点B的直线EF交☉O1于点E,交☉O2于点F.试判断CE与DF是否平行,并说明理由.
第5题
6. 如图,点C、D在以AB为直径的半圆O上,且∠ADC=120°,E是上任意一点,连接BC、BE、CE,则∠BEC的度数为 ( )
A. 20° B. 30° C. 40° D. 60°
7. (2023·淮安)如图,四边形ABCD是☉O的内接四边形,BC是☉O的直径,BC=2CD,则∠BAD的度数为 .
8. (2024·巴中改编)如图,四边形ABCD是菱形,☉O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=80°,则∠EAC的度数为 .
9. 如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在y轴的正半轴上,☉D经过A、B、O、C四点,∠ACO=120°,AB=4,则圆心D的坐标是 .
10. 如图,四边形ABCD内接于☉O,AB=CD,A为的中点,连接BD,∠BDC=60°,则∠ADB的度数为 .
11. 如图,四边形ABCD内接于☉O,∠ABC=60°,对角线DB平分∠ADC.
(1) 求证:△ABC是等边三角形;
(2) 若AD=2,DC=3,求△ABC的周长.
第11题
12. (2023·北京)如图,圆内接四边形ABCD的对角线AC、BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
(1) 求证:DB平分∠ADC,并求∠BAD的度数.
(2) 过点C作CF∥AD,交AB的延长线于点F.若AC=AD,BF=2,求此圆的半径.
第12题
2.4 圆 周 角
第1课时 圆周角的概念与性质
1. B 2. A 3. 72° 4. 34°
5. (1) ∵ AE=CE,∴ ∠A=∠C.∵ =,∴ ∠C=∠EBD,∴ ∠A=∠EBD,∴ AC∥BD (2) 连接OD、OB.∵ =,∴ ∠EDB=∠A.由(1)知,∠EBD=∠C,∠A=∠C,∴ ∠EDB=∠EBD,∴ EB=ED.∵ OE=OE,OB=OD,∴ △BOE≌△DOE,∴ ∠BEF=∠DEF
6. B 7. A 8. 40 9. 20°
10. 解析:连接AO、BO、AB.根据圆周角定理,得∠AOB=2∠C=90°.在Rt△AOB中,根据勾股定理,可得AB=2.在△CAB中,根据三角形的中位线定理,可得DG=AB=.
11. (1) ∵ =,∴ ∠B=∠E.∵ ∠B=∠D,∴ ∠E=∠D.∵ CE∥AD,∴ ∠D+∠ECD=180°,∴ ∠E+∠ECD=180°,∴ AE∥CD,∴ 四边形AECD为平行四边形 (2) 如图,连接OE、OB.∵ 四边形AECD为平行四边形,∴ AD=EC.∵ AD=BC,∴ EC=BC.又∵ OC=OC,OE=OB,∴ △COE≌△COB,∴ ∠OCE=∠OCB,即CO平分∠BCE
12. (1) 如图,设AC、BD交于点E.∵ AC⊥BD,∴ ∠AED=90°.∵ BC∥AD,∴ ∠DBC=∠ADB.∵ =,∴ ∠DBC=∠DAC,∴ ∠ADB=∠DAC,∴ 在Rt△AED中,∠ADB=∠DAC=45°.∵ OA=OD,∴ ∠OAD=∠ODA.∵ 在△OAD中,∠AOD=120°,∴ ∠OAD=30°,∴ ∠CAO=∠DAC-∠OAD=15° (2) 如图,连接OB、OC,过点O作OH⊥AD,垂足为H.∵ OA=OD,OH⊥AD,∴ AH=AD=.∵ 在Rt△OHA中,∠OAH=30°,∴ 易得OH=OA.在Rt△OHA中,由勾股定理,得OH2+AH2=OA2,∴ +=OA2,解得OA=1(负值舍去).∵ =,∴ ∠COD=2∠DAC=90°.同理,得∠AOB=90°.∵ ∠AOD=120°,∴ ∠BOC=360°-90°-90°-120°=60°.∵ OB=OC,∴ △OBC是等边三角形,∴ BC=OB.∵ OB=OA=1,∴ BC=1
第2课时 圆周角与直径的关系
1. B 2. B 3. 4. 30°
5. (1) ∵ ∠CAB=30°,∠B=60°,∴ ∠ACB=180°-∠CAB-∠B=90°.又∵ A、B两点都在圆上,∴ AB是圆的直径.又∵ O是AB的中点,∴ 点O是圆心
(2) ∵ =,∴ ∠D=∠B=60°.∵ AB⊥CD,∴ ∠DAE=90°-∠D=30°
6. B
7. D 解析:如图,连接BE、DE.由题意,得AC是左边半圆的直径,BD是右边半圆的直径.∵ B为AC的中点,∴ 点B是左边半圆的圆心.∵ 的度数为58°,∴ ∠EBC=58°.∵ BD是右边半圆的直径,∴ ∠BED=90°,∴ 在Rt△BED中,∠EDB=90°-58°=32°,∴ 的度数为32°×2=64°.
8. 90
9. ①② 解析:∵ D是的中点,∴ =,∴ ∠ABD=∠DAC.故①正确.∵ AB是半圆的直径,∴ ∠ADB=90°,∴ 在Rt△ADB中,∠DAB+∠ABD=90°.∵ DE⊥AB,∴ 在Rt△AED中,∠DAB+∠ADE=90°,∴ ∠ABD=∠ADE,∴ ∠ADE=∠DAC,∴ AF=DF.∵ 在Rt△ADG中,∠DAC+∠AGD=90°,∠ADE+∠FDG=90°,∴ ∠AGD=∠FDG,∴ DF=FG,∴ AF=FG.综上所述,正确结论的序号有①②.
10. (1) ① 如图,直线l即为所求作
② 如图,矩形ABCD即为所求作 解析:以AC为直径作☉O,以点A为圆心,在AC上方截取AB=a,交☉O于点B;以点C为圆心,在AC下方截取CD=a,交☉O于点D,连接AB、BC、CD、AD.
(2) 4
11. (1) ∵ FA=FE,∴ ∠FAE=∠AEF.∵ =,∴ ∠FAE=∠BCE.∵ ∠AEF=∠CEB,∴ ∠CEB=∠BCE.∵ CE平分∠ACD,∴ ∠ACE=∠DCE.∵ AB是☉O的直径,∴ ∠ACB=90°,即∠BCE+∠ACE=90°,∴ ∠CEB+∠DCE=90°.∵ △CDE的内角和为180°,∴ ∠CDE=90°,∴ CD⊥AB (2) 由(1)知,∠BEC=∠BCE,∴ BE=BC.∵ OM=OE=1,∴ ME=OM+OE=2.∵ AF=EF,FM⊥AB,∴ MA=ME=2,∴ AE=4,∴ OA=OB=AE-OE=3,∴ BC=BE=OB-OE=2,AB=OA+OB=6,∴ 在Rt△ABC中,AC===4
第3课时 圆的内接四边形
1. D 2. C 3. AB∥CD 4. 45°
5. CE与DF平行 理由:连接AB.∵ 四边形ABEC是☉O1的内接四边形,∴ ∠BAC+∠BEC=180°.∵ ∠BAC+∠BAD=180°,∴ ∠BAD=∠BEC.∵ 四边形ABFD是☉O2的内接四边形,∴ ∠BAD+∠BFD=180°,∴ ∠BEC+∠BFD=180°,∴ CE∥DF.
6. B 7. 120° 8. 30° 9. (-,1)
10. 40° 解析:设∠ADB=x.∵ A为的中点,∴ =,∴ ∠ABD=∠ADB=x.∵ AB=CD,∴ =,∴ ∠CBD=∠ADB=x.∵ 四边形ABCD内接于☉O,∴ ∠ABC+∠ADC=180°.∵ ∠BDC=60°,∴ 3x+60°=180°,解得x=40°,即∠ADB=40°.
11. (1) ∵ 四边形ABCD内接于☉O,∴ ∠ABC+∠ADC=180°.∵ ∠ABC=60°,∴ ∠ADC=120°.∵ DB平分∠ADC,∴ ∠ADB=∠CDB=60°.∵ =,=,∴ ∠ACB=∠ADB=60°,∠BAC=∠CDB=60°,∴ ∠ABC=∠ACB=∠BAC,∴ △ABC是等边三角形 (2) 如图,过点A作AM⊥CD,交CD的延长线于点M.∴ ∠AMD=90°.∵ ∠ADC=120°,∴ ∠ADM=180°-∠ADC=60°,∴ 在Rt△AMD中,∠DAM=30°,∴ 易得DM=AD=1,∴ AM==.∵ CD=3,∴ CM=CD+DM=4,∴ 在Rt△AMC中, AC==.∵ △ABC是等边三角形,∴ AB=BC=AC=,∴ △ABC的周长为3
12. (1) ∵ =,∴ ∠BAC=∠CDB.∵ ∠BAC=∠ADB,∴ ∠CDB=∠ADB,即DB平分∠ADC.∵ BD平分∠ABC,∴ ∠ABD=∠CBD.∵ △ABD与△CBD的内角和均为180°,∴ ∠BAD=∠BCD.∵ 四边形ABCD是圆内接四边形,∴ ∠BAD+∠BCD=180°,∴ ∠BAD=∠BCD=90° (2) ∵ ∠BAD=90°,∴ BD是圆的直径.∵ ∠ABD=∠CBD,∴ =,∴ AD=CD.∵ AC=AD,∴ AC=AD=CD,∴ △ADC是等边三角形,∴ ∠ADC=60°,∴ ∠CDB=∠ADC=30°,∴ 在Rt△BCD中,易得BD=2BC.∵ CF∥AD,∴ ∠F+∠BAD=180°,∴ ∠F=90°.∵ 四边形ABCD是圆内接四边形,∴ ∠ADC+∠ABC=180°,∴ ∠ABC=120°,∴ ∠FBC=180°-∠ABC=60°,∴ ∠FCB=90°-60°=30°,∴ 在Rt△BFC中,易得BF=BC.∵ BF=2,∴ BC=4,∴ BD=8.∵ BD是圆的直径,∴ 该圆的半径为BD=4
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
