2.6 正多边形与圆 分层练习(含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 2.6 正多边形与圆 分层练习(含答案) 2025-2026学年数学苏科版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 252.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 00:00:00 | ||
图片预览

文档简介
2.6 正多边形与圆
第1课时 正多边形与圆的关系
1. (2024·聊城)如图,AB、BC、CD是正n边形的三条边,在同一平面内,以BC为边在该正n边形的外部作正方形BCMN.若∠ABN=120°,则n的值为 ( )
A. 12 B. 10 C. 8 D. 6
2. (2023·内江)如图,正六边形ABCDEF内接于☉O,点P在上,Q是的中点,则∠CPQ的度数为 ( )
A. 30° B. 45° C. 36° D. 60°
3. (新情境·现实生活)(2024·遂宁)佩佩在“黄峨古镇”研学时学习扎染技术,得到一个内角和为1080°的正多边形图案,这个正多边形的每个外角的度数为 .
4. 如图,五边形ABCDE是正五边形.若l1∥l2,则∠1-∠2= °.
5. (2023·陕西)如图,正八边形的边长为2,对角线AB、CD相交于点E,则BE的长为 .
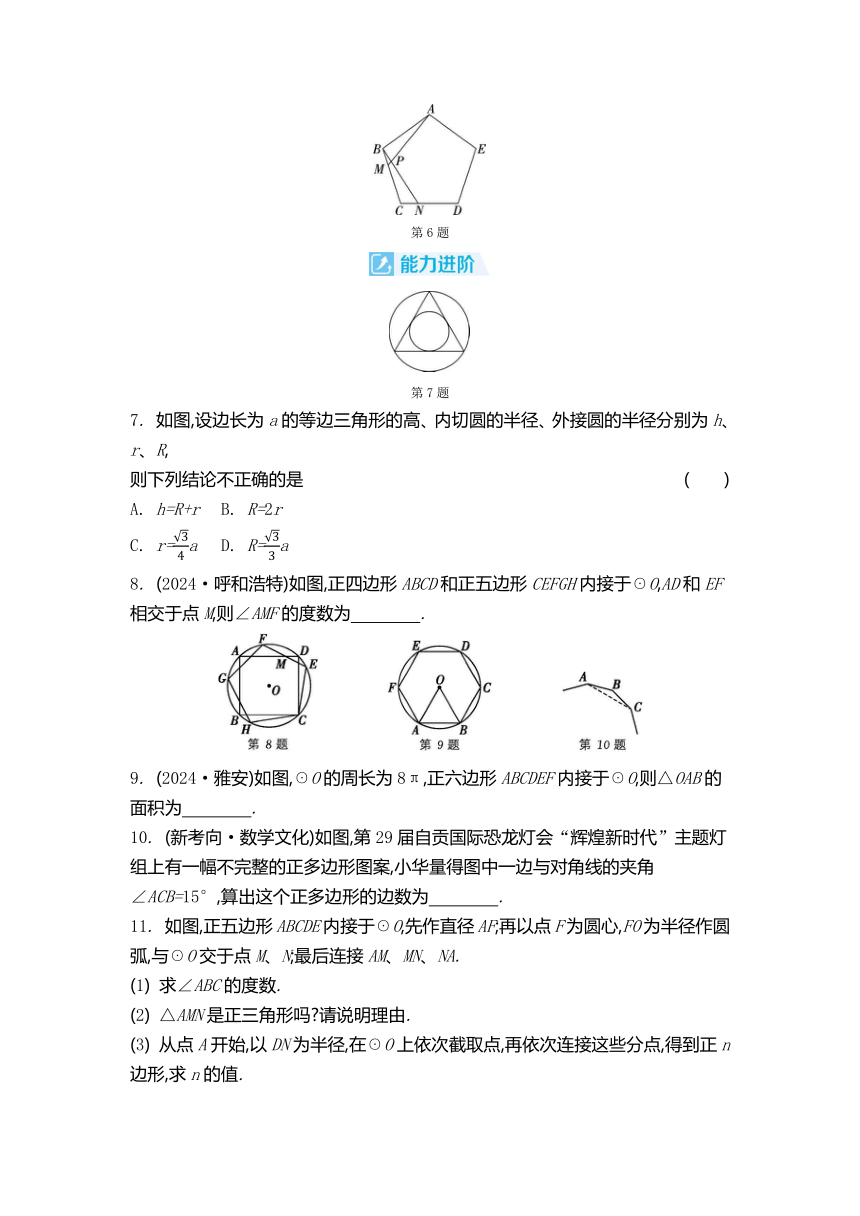
6. 如图,M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1) 求证:△ABM≌△BCN;
(2) 求∠APN的度数.
第6题
第7题
7. 如图,设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,
则下列结论不正确的是 ( )
A. h=R+r B. R=2r
C. r=a D. R=a
8. (2024·呼和浩特)如图,正四边形ABCD和正五边形CEFGH内接于☉O,AD和EF相交于点M,则∠AMF的度数为 .
9. (2024·雅安)如图,☉O的周长为8π,正六边形ABCDEF内接于☉O,则△OAB的面积为 .
10. (新考向·数学文化)如图,第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角∠ACB=15°,算出这个正多边形的边数为 .
11. 如图,正五边形ABCDE内接于☉O,先作直径AF;再以点F为圆心,FO为半径作圆弧,与☉O交于点M、N;最后连接AM、MN、NA.
(1) 求∠ABC的度数.
(2) △AMN是正三角形吗 请说明理由.
(3) 从点A开始,以DN为半径,在☉O上依次截取点,再依次连接这些分点,得到正n 边形,求n的值.
第11题
12. 如图,在正三角形ABC中,E、F、G、H、L、K分别是各边的三等分点,求证:六边形EFGHLK是正六边形.
第12题
第2课时 正多边形的对称性
1.
如图,下列五边形ABCDE都是正五边形,则这些图形中是轴对称图形的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
2. 有下列说法:① 正多边形的各条边相等;② 各边相等的多边形是正多边形;③ 各角相等的多边形是正多边形;④ 各边相等的圆的内接多边形是正多边形;⑤ 既是轴对称图形,又是中心对称图形的多边形是正多边形.其中,正确的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
3. 每个外角都是20°的正多边形的对称轴一共有 条.
4. 将一个正七边形绕它的中心旋转,至少要旋转 °才能与原来的图形重合.
5. 如图,将☉O八等分,得到,将☉O十二等分,得到,连接BC.若线段BC是☉O的内接正n边形的一条边,试探究n的值.
第5题
6. (新考向·传统文化)(2024·东营)我国魏晋时期的数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来估算圆周率π的值.如图,☉O的半径为1,运用“割圆术”,以圆内接正六边形的面积来估计☉O的面积,可得π的估计值为.若用圆内接正八边形进行估计,则π的估计值为 ( )
A. B. 2 C. 3 D. 2
7. (易错题)如图所示为一种警报装置的示意图,电子屏幕上有一个正六边形ABCDEF,点P沿直线AB从右向左移动,当出现点P与正六边形六个顶点中的至少两个顶点距离相等时,就会发出警报,则直线AB上会发出警报的点P有 个.
8. 如图,在平面直角坐标系中,有一个正六边形ABCDEF,其中C、D两点的坐标分别为(1,0)、(2,0).若在无滑动的情况下,将这个正六边形沿着x轴向右滚动,则在滚动的过程中,这个正六边形的顶点A、B、C、D、E、F会过点(45,2)的是 .
9. 如图①所示为地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图②,AE是☉O的直径,用无刻度的直尺和圆规作☉O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).
10. (1) 如图①,△ABC是☉O的内接正三角形,P为上一动点,连接PA、PB、PC.求证:PA=PB+PC.
(2) 如图②,四边形ABCD是☉O的内接正方形,P为上一动点,连接PA、PB、PC.求证:PA=PC+PB.
(3) 如图③,六边形ABCDEF是☉O的内接正六边形,P为上一动点,连接PA、PB、PC.请探究PA、PB、PC三者之间的数量关系,直接写出答案,不必证明.
2.6 正多边形与圆
第1课时 正多边形与圆的关系
1. A 2. B 3. 45° 4. 72 5. 2+
6. (1) 在正五边形ABCDE中,AB=BC,∠ABM=∠C.在△ABM和△BCN中,∴ △ABM≌△BCN (2) ∵ △ABM≌△BCN,∴ ∠BAM=∠CBN.∵ ∠BAM+∠ABP=∠APN,∴ ∠APN=∠CBN+∠ABP=∠ABC==108°
7. C
8. 27° 解析:如图,连接OG、OF、OD、OE、DF、AC.∵ 四边形ABCD是正方形,∴ ∠ADC=90°,∴ AC过圆心O,∴ ∠AOD=×360°=90°,∠FOG=∠EOF=×360°=72°.∵ 正五边形CEFGH内接于☉O,∴ ===,∴ =,∴ ∠GOC=∠FOC,∴ ∠AOG=∠AOF=∠FOG=36°,∴ ∠DOF=90°-36°=54°,∴ ∠DOE=72°-54°=18°,∴ ∠AMF=∠MFD+∠MDF=∠DOE+∠AOF=×18°+×36°=27°.
9. 4 10. 12
11. (1)∵ 五边形ABCDE是正五边形,∴ ∠ABC==108° (2) △AMN是正三角形 理由:连接ON、NF.由作图,得FN=OF.∵ OF=ON,∴ FN=OF=ON,∴ △FON是等边三角形,∴ ∠NFA=60°.∵ =,∴ ∠NMA=∠NFA=60°.同理,可得∠ANM=60°,∴ 在△AMN中,∠MAN=60°,∴ ∠NMA=∠ANM=∠MAN,∴ △AMN是正三角形.
(3) 由(2),得△AMN是正三角形,∴ ∠AON=2∠AMN=120°,∴ =120°.∵ =2=2×=144°,∴ =-=24°,∴ n==15
12. ∵ △ABC是等边三角形,∴ ∠A=∠B=∠C=60°,AB=BC=AC.∵ E、F、G、H、L、K分别是各边的三等分点,∴ AE=EF=FB=AB,BG=GH=HC=BC,LC=KL=AK=AC,∴ AE=AK,BF=BG,CH=CL.∵ ∠A=∠B=∠C=60°,∴ △AEK、△BGF、△CHL是等边三角形,∴ EK=EF=FG=GH=HL=LK,∠KEF=∠EFG=∠FGH=∠GHL=∠HLK=∠LKE=120°,∴ 六边形EFGHLK是正六边形
第2课时 正多边形的对称性
1. D 2. B 3. 18 4.
5. 连接AO、CO.由题意,得的度数为=45°,的度数为=30°,∴ 的度数为45°-30°=15°.∵ 360°÷15°=24,∴ 线段BC是☉O的内接正二十四边形的一条边,∴ n=24
6. B
7. 5 [易错分析]解答本题时容易忽视正六边形的对角线EC、AC的垂直平分线分别与直线AB的交点也是符合题意的点.
8. B
9. 如图
10. (1) 如图①,延长BP至点E,使PE=PC,连接CE.∵ A、B、P、C四点在同一个圆上,∴ ∠BAC+∠BPC=180°.∵ ∠BPC+∠CPE=180°,∴ ∠BAC=∠CPE.∵ △ABC为正三角形,∴ ∠BAC=∠ACB=60°,∴ ∠CPE=60°.又∵ PE=PC,∴ △PCE是正三角形,∴ ∠PCE=60°.∵ ∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,∴ ∠BCE=∠ACP.∵ △PCE、△ABC为正三角形,∴ CP=CE,AC=BC,∴ △APC≌△BEC,∴ PA=EB=PB+PE=PB+PC (2) 如图②,过点B作BE⊥PB,交PA于点E,连接AC.∵ ∠ABE+∠EBC=∠EBC+∠CBP=90°,∴ ∠ABE=∠CBP.∵ 四边形ABCD是正方形,∴ AB=CB,∠ACB=45°,∴ ∠APB=∠ACB=45°,∴ 在Rt△EBP中,∠BEP=∠APB=45°,∴ BE=BP,∴ 根据勾股定理,易得PE=PB.又∵ AB=CB,∴ △ABE≌△CBP,∴ EA=PC,∴ PA=EA+PE=PC+PB (3) PA=PC+PB
第1课时 正多边形与圆的关系
1. (2024·聊城)如图,AB、BC、CD是正n边形的三条边,在同一平面内,以BC为边在该正n边形的外部作正方形BCMN.若∠ABN=120°,则n的值为 ( )
A. 12 B. 10 C. 8 D. 6
2. (2023·内江)如图,正六边形ABCDEF内接于☉O,点P在上,Q是的中点,则∠CPQ的度数为 ( )
A. 30° B. 45° C. 36° D. 60°
3. (新情境·现实生活)(2024·遂宁)佩佩在“黄峨古镇”研学时学习扎染技术,得到一个内角和为1080°的正多边形图案,这个正多边形的每个外角的度数为 .
4. 如图,五边形ABCDE是正五边形.若l1∥l2,则∠1-∠2= °.
5. (2023·陕西)如图,正八边形的边长为2,对角线AB、CD相交于点E,则BE的长为 .
6. 如图,M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1) 求证:△ABM≌△BCN;
(2) 求∠APN的度数.
第6题
第7题
7. 如图,设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,
则下列结论不正确的是 ( )
A. h=R+r B. R=2r
C. r=a D. R=a
8. (2024·呼和浩特)如图,正四边形ABCD和正五边形CEFGH内接于☉O,AD和EF相交于点M,则∠AMF的度数为 .
9. (2024·雅安)如图,☉O的周长为8π,正六边形ABCDEF内接于☉O,则△OAB的面积为 .
10. (新考向·数学文化)如图,第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角∠ACB=15°,算出这个正多边形的边数为 .
11. 如图,正五边形ABCDE内接于☉O,先作直径AF;再以点F为圆心,FO为半径作圆弧,与☉O交于点M、N;最后连接AM、MN、NA.
(1) 求∠ABC的度数.
(2) △AMN是正三角形吗 请说明理由.
(3) 从点A开始,以DN为半径,在☉O上依次截取点,再依次连接这些分点,得到正n 边形,求n的值.
第11题
12. 如图,在正三角形ABC中,E、F、G、H、L、K分别是各边的三等分点,求证:六边形EFGHLK是正六边形.
第12题
第2课时 正多边形的对称性
1.
如图,下列五边形ABCDE都是正五边形,则这些图形中是轴对称图形的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
2. 有下列说法:① 正多边形的各条边相等;② 各边相等的多边形是正多边形;③ 各角相等的多边形是正多边形;④ 各边相等的圆的内接多边形是正多边形;⑤ 既是轴对称图形,又是中心对称图形的多边形是正多边形.其中,正确的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
3. 每个外角都是20°的正多边形的对称轴一共有 条.
4. 将一个正七边形绕它的中心旋转,至少要旋转 °才能与原来的图形重合.
5. 如图,将☉O八等分,得到,将☉O十二等分,得到,连接BC.若线段BC是☉O的内接正n边形的一条边,试探究n的值.
第5题
6. (新考向·传统文化)(2024·东营)我国魏晋时期的数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来估算圆周率π的值.如图,☉O的半径为1,运用“割圆术”,以圆内接正六边形的面积来估计☉O的面积,可得π的估计值为.若用圆内接正八边形进行估计,则π的估计值为 ( )
A. B. 2 C. 3 D. 2
7. (易错题)如图所示为一种警报装置的示意图,电子屏幕上有一个正六边形ABCDEF,点P沿直线AB从右向左移动,当出现点P与正六边形六个顶点中的至少两个顶点距离相等时,就会发出警报,则直线AB上会发出警报的点P有 个.
8. 如图,在平面直角坐标系中,有一个正六边形ABCDEF,其中C、D两点的坐标分别为(1,0)、(2,0).若在无滑动的情况下,将这个正六边形沿着x轴向右滚动,则在滚动的过程中,这个正六边形的顶点A、B、C、D、E、F会过点(45,2)的是 .
9. 如图①所示为地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图②,AE是☉O的直径,用无刻度的直尺和圆规作☉O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).
10. (1) 如图①,△ABC是☉O的内接正三角形,P为上一动点,连接PA、PB、PC.求证:PA=PB+PC.
(2) 如图②,四边形ABCD是☉O的内接正方形,P为上一动点,连接PA、PB、PC.求证:PA=PC+PB.
(3) 如图③,六边形ABCDEF是☉O的内接正六边形,P为上一动点,连接PA、PB、PC.请探究PA、PB、PC三者之间的数量关系,直接写出答案,不必证明.
2.6 正多边形与圆
第1课时 正多边形与圆的关系
1. A 2. B 3. 45° 4. 72 5. 2+
6. (1) 在正五边形ABCDE中,AB=BC,∠ABM=∠C.在△ABM和△BCN中,∴ △ABM≌△BCN (2) ∵ △ABM≌△BCN,∴ ∠BAM=∠CBN.∵ ∠BAM+∠ABP=∠APN,∴ ∠APN=∠CBN+∠ABP=∠ABC==108°
7. C
8. 27° 解析:如图,连接OG、OF、OD、OE、DF、AC.∵ 四边形ABCD是正方形,∴ ∠ADC=90°,∴ AC过圆心O,∴ ∠AOD=×360°=90°,∠FOG=∠EOF=×360°=72°.∵ 正五边形CEFGH内接于☉O,∴ ===,∴ =,∴ ∠GOC=∠FOC,∴ ∠AOG=∠AOF=∠FOG=36°,∴ ∠DOF=90°-36°=54°,∴ ∠DOE=72°-54°=18°,∴ ∠AMF=∠MFD+∠MDF=∠DOE+∠AOF=×18°+×36°=27°.
9. 4 10. 12
11. (1)∵ 五边形ABCDE是正五边形,∴ ∠ABC==108° (2) △AMN是正三角形 理由:连接ON、NF.由作图,得FN=OF.∵ OF=ON,∴ FN=OF=ON,∴ △FON是等边三角形,∴ ∠NFA=60°.∵ =,∴ ∠NMA=∠NFA=60°.同理,可得∠ANM=60°,∴ 在△AMN中,∠MAN=60°,∴ ∠NMA=∠ANM=∠MAN,∴ △AMN是正三角形.
(3) 由(2),得△AMN是正三角形,∴ ∠AON=2∠AMN=120°,∴ =120°.∵ =2=2×=144°,∴ =-=24°,∴ n==15
12. ∵ △ABC是等边三角形,∴ ∠A=∠B=∠C=60°,AB=BC=AC.∵ E、F、G、H、L、K分别是各边的三等分点,∴ AE=EF=FB=AB,BG=GH=HC=BC,LC=KL=AK=AC,∴ AE=AK,BF=BG,CH=CL.∵ ∠A=∠B=∠C=60°,∴ △AEK、△BGF、△CHL是等边三角形,∴ EK=EF=FG=GH=HL=LK,∠KEF=∠EFG=∠FGH=∠GHL=∠HLK=∠LKE=120°,∴ 六边形EFGHLK是正六边形
第2课时 正多边形的对称性
1. D 2. B 3. 18 4.
5. 连接AO、CO.由题意,得的度数为=45°,的度数为=30°,∴ 的度数为45°-30°=15°.∵ 360°÷15°=24,∴ 线段BC是☉O的内接正二十四边形的一条边,∴ n=24
6. B
7. 5 [易错分析]解答本题时容易忽视正六边形的对角线EC、AC的垂直平分线分别与直线AB的交点也是符合题意的点.
8. B
9. 如图
10. (1) 如图①,延长BP至点E,使PE=PC,连接CE.∵ A、B、P、C四点在同一个圆上,∴ ∠BAC+∠BPC=180°.∵ ∠BPC+∠CPE=180°,∴ ∠BAC=∠CPE.∵ △ABC为正三角形,∴ ∠BAC=∠ACB=60°,∴ ∠CPE=60°.又∵ PE=PC,∴ △PCE是正三角形,∴ ∠PCE=60°.∵ ∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,∴ ∠BCE=∠ACP.∵ △PCE、△ABC为正三角形,∴ CP=CE,AC=BC,∴ △APC≌△BEC,∴ PA=EB=PB+PE=PB+PC (2) 如图②,过点B作BE⊥PB,交PA于点E,连接AC.∵ ∠ABE+∠EBC=∠EBC+∠CBP=90°,∴ ∠ABE=∠CBP.∵ 四边形ABCD是正方形,∴ AB=CB,∠ACB=45°,∴ ∠APB=∠ACB=45°,∴ 在Rt△EBP中,∠BEP=∠APB=45°,∴ BE=BP,∴ 根据勾股定理,易得PE=PB.又∵ AB=CB,∴ △ABE≌△CBP,∴ EA=PC,∴ PA=EA+PE=PC+PB (3) PA=PC+PB
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
