第1章一元二次方程 素能测评(含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 第1章一元二次方程 素能测评(含答案) 2025-2026学年数学苏科版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 53.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 14:39:23 | ||
图片预览


文档简介
第1章一元二次方程 素能测评满分:130分
时间:120分钟
一、 选择题(每小题3分,共24分)
1.
下列方程中,一定是关于x的一元二次方程的为 ( )
A. ax2+bx+c=0 B. 5x-2x2+7=0
C. 2y2-x-3=0 D. mx2-2x=x2+1
2. 用配方法解方程x2+4x+1=0时,配方正确的是 ( )
A. (x-2)2=5 B. (x-2)2=3
C. (x+2)2=5 D. (x+2)2=3
3. 若x=3是关于x的一元二次方程x2-ax-a2=0(a>0)的一个根,则下列对a的值估计正确的是 ( )
A.C. 4. 若关于x的一元二次方程x2-4x+c=0有两个相等的实数根,则实数c的值为 ( )
A. -16 B. -4 C. 4 D. 16
5. 小影与小冬一起写作业,解一道一元二次方程时,小影在化简过程中写错了常数项,因而得到方程的两个根是6和1;小冬在化简过程中写错了一次项的系数,因而得到方程的两个根是-2和-5.原来的方程可以是 ( )
A. x2+6x+5=0 B. x2-7x+10=0
C. x2-5x+2=0 D. x2-6x-10=0
6. 已知实数a、b满足(a2+b2)2-2(a2+b2)=8,则a2+b2的值为 ( )
A. 2 B. 4 C. 4或-2 D. -4或2
7. 已知关于x的一元二次方程x2-mx-n2+mn+1=0,其中m、n满足m-2n=3,关于该方程根的情况,下列判断正确的是 ( )
A. 没有实数根 B. 有两个相等的实数根
C. 有两个不相等的实数根 D. 无法确定
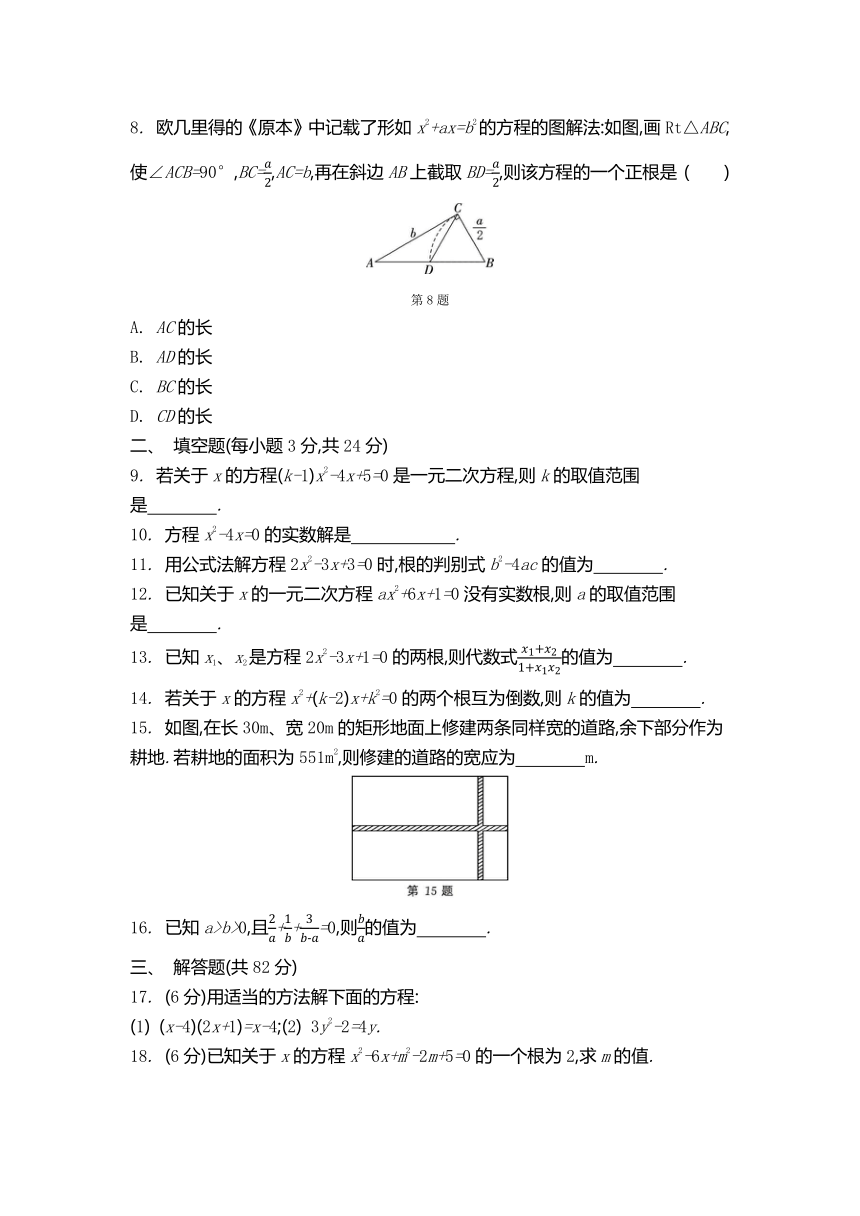
8. 欧几里得的《原本》中记载了形如x2+ax=b2的方程的图解法:如图,画Rt△ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=,则该方程的一个正根是 ( )
第8题
A. AC的长
B. AD的长
C. BC的长
D. CD的长
二、 填空题(每小题3分,共24分)
9. 若关于x的方程(k-1)x2-4x+5=0是一元二次方程,则k的取值范围是 .
10. 方程x2-4x=0的实数解是 .
11. 用公式法解方程2x2-3x+3=0时,根的判别式b2-4ac的值为 .
12. 已知关于x的一元二次方程ax2+6x+1=0没有实数根,则a的取值范围是 .
13. 已知x1、x2是方程2x2-3x+1=0的两根,则代数式的值为 .
14. 若关于x的方程x2+(k-2)x+k2=0的两个根互为倒数,则k的值为 .
15. 如图,在长30m、宽20m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地的面积为551m2,则修建的道路的宽应为 m.
16. 已知a>b>0,且++=0,则的值为 .
三、 解答题(共82分)
17. (6分)用适当的方法解下面的方程:
(1) (x-4)(2x+1)=x-4; (2) 3y2-2=4y.
18. (6分)已知关于x的方程x2-6x+m2-2m+5=0的一个根为2,求m的值.
19. (6分)若△ABC是等腰三角形,AB=4,另外两边长是关于x的一元二次方程x2-2mx+m2-1=0的根,求△ABC的周长.
20. (6分)设一元二次方程x2+bx+c=0.有下列四组条件:① b=2,c=1;② b=3,c=1;③ b=3,c=-1;④ b=2,c=2.选择其中一组b、c的值,使这个方程有两个不相等的实数根,并解这个方程.
21. (6分)在实数范围内,对于任意实数m、n(m≠0),规定一种新运算:m n=mn+mn-3,例如:3 2=32+3×2-3=12.
(1) (-2) 3的值为 ;
(2) 若(-y) 2的值为4,求y的值.
22. (8分)已知关于x的一元二次方程x2-2(m-1)x+m2=0有实数根.
(1) 求m的取值范围;
(2) 设此方程的两个根分别为x1、x2,若+=8-3x1x2,求m的值.
23. (8分)一个两位数的个位数字与十位数字的和为11,并且个位数字与十位数字的平方和为85,求这个两位数.
24. (8分)为满足市场需求,某超市在端午节前夕购进价格为每个3元的某品牌粽子,根据市场预测,当该品牌粽子每个的售价为4元时,每天能售出500个,并且每个的售价每上涨0.1元,其销售量将减少10个.为了维护消费者的利益,物价部门规定,该品牌粽子的售价不能超过进价的200%.若超市计划每天销售该品牌的粽子获得的利润为800元,则应如何定价
25. (8分)如图,李伯伯想用长为70m的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD,并在边BC上留一个2m宽的门(建在EF处,且用的是其他材料).
(1) 当矩形羊圈的长和宽分别为多少米时,能围成一个面积为640m2的矩形羊圈
(2) 矩形羊圈的面积能达到650m2吗 如果能,请你给出设计方案;如果不能,请说明理由.
第25题
26. (10分)“秋风起,蟹脚痒”,随着大闸蟹的大量上市,某大闸蟹销售公司前三个月的月销售利润逐月增长,第1个月的销售利润为20万元,第3个月的销售利润为28.8万元,假设从第1个月到第3个月每月销售利润的平均增长率相同.
(1) 求从第1个月到第3个月每月销售利润的平均增长率;
(2) 进入第4个月,大闸蟹产量逐渐下降,第4个月的销售利润比第3个月的销售利润下降了20%,求从第1个月到第4个月的销售利润之和.
27. (10分)如图,正方形ABCD的边长为4cm,动点P从点B出发,以2cm/s的速度沿B→C→D的方向向点D运动;动点Q从点A出发,以1cm/s的速度沿A→B的方向向点B运动.若P、Q两点同时出发,运动时间为ts.连接PD、PQ、DQ,当点P在BC上运动时,是否存在t的值,使△PQD是以PD为一腰的等腰三角形 若存在,请求出符合条件的t的值;若不存在,请说明理由.
第27题
第1章素能测评
一、 1. B 2. D 3. B 4. C 5. B 6. B
7. C 解析:∵ m-2n=3,∴ 根的判别式为(-m)2-4(-n2+mn+1)=m2+4n2-4mn-4=(m-2n)2-4=32-4=9-4=5>0,∴ 原方程有两个不相等的实数根.
8. B
二、 9. k≠1 10. x1=0,x2=4 11. -15 12. a>9
13. 1 14. -1 15. 1
16. 解析:∵ ++=0,∴ =0.∵ a>b>0,∴ ab(b-a)≠0,∴ 2b(b-a)+a(b-a)+3ab=0,即2b2-a2+2ab=0.∵ ab≠0,∴ 2·-+2=0.令=t.∵ a>b>0,∴ 0三、 17. (1) x1=4,x2=0 (2) y1=,y2=
18. 把x=2代入方程x2-6x+m2-2m+5=0,得4-12+m2-2m+5=0,整理,得m2-2m-3=0,即(m-3)(m+1)=0,∴ m1=3,m2=-1,∴ m的值为3或-1
19. 方程x2-2mx+m2-1=0可化为x2-2mx+(m+1)(m-1)=0,即[x-(m+1)][x-(m-1)]=0,∴ x1=m+1,x2=m-1.当m+1=4时,解得m=3,此时等腰三角形的三边长分别为4、4、2,△ABC的周长为4+4+2=10;当m-1=4时,解得m=5,此时等腰三角形的三边长分别为4、4、6,△ABC的周长为4+4+6=14.∴ △ABC的周长为10或14
20. ∵ 方程x2+bx+c=0有两个不相等的实数根,∴ b2-4ac>0,即b2>4c,∴ 只有②③满足.若选择②,则这个方程为x2+3x+1=0,∴ x==,此时x1=,x2=.若选择③,则这个方程为x2+3x-1=0,∴ x==,此时x1=,x2=
21. (1) -17 (2) 根据题意,得(-y) 2=4,∴ (-y)2+2·(-y)-3=4,整理,得y2-2y-7=0,∴ y1=1+2,y2=1-2,∴ y的值为1+2或1-2
22. (1) ∵ 关于x的一元二次方程x2-2(m-1)x+m2=0有实数根,∴ b2-4ac=[-2(m-1)]2-4m2=4-8m≥0,解得m≤ (2) ∵ 关于x的一元二次方程x2-2(m-1)x+m2=0的两个根分别为x1、x2,∴ x1+x2=2m-2,x1x2=m2.∵ +=8-3x1x2,∴ (x1+x2)2-2x1x2=8-3x1x2,即5m2-8m-4=0,解得m1=-,m2=2(不合题意,舍去),∴ m的值为-
23. 设这个两位数的个位数字为x,则它的十位数字为(11-x).根据题意,得x2+(11-x)2=85,解得x1=2,x2=9.当x=2时,这个两位数为92;当x=9时,这个两位数为29.答:这个两位数为92或29
24. 设当该品牌粽子每个的售价为x元时,超市每天销售该品牌的粽子获得的利润为800元.根据题意,得(x-3)500-10×=800,解得x1=7,x2=5.∵ 售价不能超过进价的200%,∴ x≤3×200%,即x≤6,∴ x=5.答:超市应将该品牌粽子每个的售价定为5元
25. (1) 设边AB=xm,则边BC=70-2x+2=(72-2x)m.根据题意,得x(72-2x)=640.整理,得x2-36x+320=0,解得x1=16,x2=20.当x=16时,72-2x=40;当x=20时,72-2x=32.答:当矩形羊圈的长为40m,宽为16m或长为32m,宽为20m时,能围成一个面积为640m2的矩形羊圈 (2) 不能 理由:根据题意,令x(72-2x)=650.整理,得x2-36x+325=0.∵ (-36)2-4×1×325=-4<0,∴ 一元二次方程没有实数根,∴ 矩形羊圈的面积不能达到650m2.
26. (1) 设从第1个月到第3个月每月销售利润的平均增长率为x.根据题意,得20(1+x)2=28.8,解得x1=0.2=20%,x2=-2.2(不合题意,舍去).答:从第1个月到第3个月每月销售利润的平均增长率为20% (2) 从第1个月到第4个月的销售利润之和为20+20×(1+20%)+28.8+28.8×(1-20%)=20+24+28.8+23.04=95.84(万元)
27. 存在 由题意,得AQ=tcm,BQ=(4-t)cm,BP=2tcm,PC=(4-2t)cm.由题意,得0≤t≤2.当PD=QD时,由题意,得∠C=∠A=90°,DC=DA,∴ Rt△DPC≌Rt△DQA,∴ PC=QA,即4-2t=t,解得t=.当PD=PQ时,在Rt△PBQ中,PQ2=PB2+BQ2,在Rt△PCD中,PD2=PC2+CD2,∴ (2t)2+(4-t)2=(4-2t)2+42,解得t1=-4-4(不合题意,舍去),t2=4-4.∴ 存在t的值,使△PQD是以PD为一腰的等腰三角形,t的值为或4-4
时间:120分钟
一、 选择题(每小题3分,共24分)
1.
下列方程中,一定是关于x的一元二次方程的为 ( )
A. ax2+bx+c=0 B. 5x-2x2+7=0
C. 2y2-x-3=0 D. mx2-2x=x2+1
2. 用配方法解方程x2+4x+1=0时,配方正确的是 ( )
A. (x-2)2=5 B. (x-2)2=3
C. (x+2)2=5 D. (x+2)2=3
3. 若x=3是关于x的一元二次方程x2-ax-a2=0(a>0)的一个根,则下列对a的值估计正确的是 ( )
A.
A. -16 B. -4 C. 4 D. 16
5. 小影与小冬一起写作业,解一道一元二次方程时,小影在化简过程中写错了常数项,因而得到方程的两个根是6和1;小冬在化简过程中写错了一次项的系数,因而得到方程的两个根是-2和-5.原来的方程可以是 ( )
A. x2+6x+5=0 B. x2-7x+10=0
C. x2-5x+2=0 D. x2-6x-10=0
6. 已知实数a、b满足(a2+b2)2-2(a2+b2)=8,则a2+b2的值为 ( )
A. 2 B. 4 C. 4或-2 D. -4或2
7. 已知关于x的一元二次方程x2-mx-n2+mn+1=0,其中m、n满足m-2n=3,关于该方程根的情况,下列判断正确的是 ( )
A. 没有实数根 B. 有两个相等的实数根
C. 有两个不相等的实数根 D. 无法确定
8. 欧几里得的《原本》中记载了形如x2+ax=b2的方程的图解法:如图,画Rt△ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=,则该方程的一个正根是 ( )
第8题
A. AC的长
B. AD的长
C. BC的长
D. CD的长
二、 填空题(每小题3分,共24分)
9. 若关于x的方程(k-1)x2-4x+5=0是一元二次方程,则k的取值范围是 .
10. 方程x2-4x=0的实数解是 .
11. 用公式法解方程2x2-3x+3=0时,根的判别式b2-4ac的值为 .
12. 已知关于x的一元二次方程ax2+6x+1=0没有实数根,则a的取值范围是 .
13. 已知x1、x2是方程2x2-3x+1=0的两根,则代数式的值为 .
14. 若关于x的方程x2+(k-2)x+k2=0的两个根互为倒数,则k的值为 .
15. 如图,在长30m、宽20m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地的面积为551m2,则修建的道路的宽应为 m.
16. 已知a>b>0,且++=0,则的值为 .
三、 解答题(共82分)
17. (6分)用适当的方法解下面的方程:
(1) (x-4)(2x+1)=x-4; (2) 3y2-2=4y.
18. (6分)已知关于x的方程x2-6x+m2-2m+5=0的一个根为2,求m的值.
19. (6分)若△ABC是等腰三角形,AB=4,另外两边长是关于x的一元二次方程x2-2mx+m2-1=0的根,求△ABC的周长.
20. (6分)设一元二次方程x2+bx+c=0.有下列四组条件:① b=2,c=1;② b=3,c=1;③ b=3,c=-1;④ b=2,c=2.选择其中一组b、c的值,使这个方程有两个不相等的实数根,并解这个方程.
21. (6分)在实数范围内,对于任意实数m、n(m≠0),规定一种新运算:m n=mn+mn-3,例如:3 2=32+3×2-3=12.
(1) (-2) 3的值为 ;
(2) 若(-y) 2的值为4,求y的值.
22. (8分)已知关于x的一元二次方程x2-2(m-1)x+m2=0有实数根.
(1) 求m的取值范围;
(2) 设此方程的两个根分别为x1、x2,若+=8-3x1x2,求m的值.
23. (8分)一个两位数的个位数字与十位数字的和为11,并且个位数字与十位数字的平方和为85,求这个两位数.
24. (8分)为满足市场需求,某超市在端午节前夕购进价格为每个3元的某品牌粽子,根据市场预测,当该品牌粽子每个的售价为4元时,每天能售出500个,并且每个的售价每上涨0.1元,其销售量将减少10个.为了维护消费者的利益,物价部门规定,该品牌粽子的售价不能超过进价的200%.若超市计划每天销售该品牌的粽子获得的利润为800元,则应如何定价
25. (8分)如图,李伯伯想用长为70m的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD,并在边BC上留一个2m宽的门(建在EF处,且用的是其他材料).
(1) 当矩形羊圈的长和宽分别为多少米时,能围成一个面积为640m2的矩形羊圈
(2) 矩形羊圈的面积能达到650m2吗 如果能,请你给出设计方案;如果不能,请说明理由.
第25题
26. (10分)“秋风起,蟹脚痒”,随着大闸蟹的大量上市,某大闸蟹销售公司前三个月的月销售利润逐月增长,第1个月的销售利润为20万元,第3个月的销售利润为28.8万元,假设从第1个月到第3个月每月销售利润的平均增长率相同.
(1) 求从第1个月到第3个月每月销售利润的平均增长率;
(2) 进入第4个月,大闸蟹产量逐渐下降,第4个月的销售利润比第3个月的销售利润下降了20%,求从第1个月到第4个月的销售利润之和.
27. (10分)如图,正方形ABCD的边长为4cm,动点P从点B出发,以2cm/s的速度沿B→C→D的方向向点D运动;动点Q从点A出发,以1cm/s的速度沿A→B的方向向点B运动.若P、Q两点同时出发,运动时间为ts.连接PD、PQ、DQ,当点P在BC上运动时,是否存在t的值,使△PQD是以PD为一腰的等腰三角形 若存在,请求出符合条件的t的值;若不存在,请说明理由.
第27题
第1章素能测评
一、 1. B 2. D 3. B 4. C 5. B 6. B
7. C 解析:∵ m-2n=3,∴ 根的判别式为(-m)2-4(-n2+mn+1)=m2+4n2-4mn-4=(m-2n)2-4=32-4=9-4=5>0,∴ 原方程有两个不相等的实数根.
8. B
二、 9. k≠1 10. x1=0,x2=4 11. -15 12. a>9
13. 1 14. -1 15. 1
16. 解析:∵ ++=0,∴ =0.∵ a>b>0,∴ ab(b-a)≠0,∴ 2b(b-a)+a(b-a)+3ab=0,即2b2-a2+2ab=0.∵ ab≠0,∴ 2·-+2=0.令=t.∵ a>b>0,∴ 0
18. 把x=2代入方程x2-6x+m2-2m+5=0,得4-12+m2-2m+5=0,整理,得m2-2m-3=0,即(m-3)(m+1)=0,∴ m1=3,m2=-1,∴ m的值为3或-1
19. 方程x2-2mx+m2-1=0可化为x2-2mx+(m+1)(m-1)=0,即[x-(m+1)][x-(m-1)]=0,∴ x1=m+1,x2=m-1.当m+1=4时,解得m=3,此时等腰三角形的三边长分别为4、4、2,△ABC的周长为4+4+2=10;当m-1=4时,解得m=5,此时等腰三角形的三边长分别为4、4、6,△ABC的周长为4+4+6=14.∴ △ABC的周长为10或14
20. ∵ 方程x2+bx+c=0有两个不相等的实数根,∴ b2-4ac>0,即b2>4c,∴ 只有②③满足.若选择②,则这个方程为x2+3x+1=0,∴ x==,此时x1=,x2=.若选择③,则这个方程为x2+3x-1=0,∴ x==,此时x1=,x2=
21. (1) -17 (2) 根据题意,得(-y) 2=4,∴ (-y)2+2·(-y)-3=4,整理,得y2-2y-7=0,∴ y1=1+2,y2=1-2,∴ y的值为1+2或1-2
22. (1) ∵ 关于x的一元二次方程x2-2(m-1)x+m2=0有实数根,∴ b2-4ac=[-2(m-1)]2-4m2=4-8m≥0,解得m≤ (2) ∵ 关于x的一元二次方程x2-2(m-1)x+m2=0的两个根分别为x1、x2,∴ x1+x2=2m-2,x1x2=m2.∵ +=8-3x1x2,∴ (x1+x2)2-2x1x2=8-3x1x2,即5m2-8m-4=0,解得m1=-,m2=2(不合题意,舍去),∴ m的值为-
23. 设这个两位数的个位数字为x,则它的十位数字为(11-x).根据题意,得x2+(11-x)2=85,解得x1=2,x2=9.当x=2时,这个两位数为92;当x=9时,这个两位数为29.答:这个两位数为92或29
24. 设当该品牌粽子每个的售价为x元时,超市每天销售该品牌的粽子获得的利润为800元.根据题意,得(x-3)500-10×=800,解得x1=7,x2=5.∵ 售价不能超过进价的200%,∴ x≤3×200%,即x≤6,∴ x=5.答:超市应将该品牌粽子每个的售价定为5元
25. (1) 设边AB=xm,则边BC=70-2x+2=(72-2x)m.根据题意,得x(72-2x)=640.整理,得x2-36x+320=0,解得x1=16,x2=20.当x=16时,72-2x=40;当x=20时,72-2x=32.答:当矩形羊圈的长为40m,宽为16m或长为32m,宽为20m时,能围成一个面积为640m2的矩形羊圈 (2) 不能 理由:根据题意,令x(72-2x)=650.整理,得x2-36x+325=0.∵ (-36)2-4×1×325=-4<0,∴ 一元二次方程没有实数根,∴ 矩形羊圈的面积不能达到650m2.
26. (1) 设从第1个月到第3个月每月销售利润的平均增长率为x.根据题意,得20(1+x)2=28.8,解得x1=0.2=20%,x2=-2.2(不合题意,舍去).答:从第1个月到第3个月每月销售利润的平均增长率为20% (2) 从第1个月到第4个月的销售利润之和为20+20×(1+20%)+28.8+28.8×(1-20%)=20+24+28.8+23.04=95.84(万元)
27. 存在 由题意,得AQ=tcm,BQ=(4-t)cm,BP=2tcm,PC=(4-2t)cm.由题意,得0≤t≤2.当PD=QD时,由题意,得∠C=∠A=90°,DC=DA,∴ Rt△DPC≌Rt△DQA,∴ PC=QA,即4-2t=t,解得t=.当PD=PQ时,在Rt△PBQ中,PQ2=PB2+BQ2,在Rt△PCD中,PD2=PC2+CD2,∴ (2t)2+(4-t)2=(4-2t)2+42,解得t1=-4-4(不合题意,舍去),t2=4-4.∴ 存在t的值,使△PQD是以PD为一腰的等腰三角形,t的值为或4-4
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
