第2章 对称图形——圆 素能测评 (含答案)2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 第2章 对称图形——圆 素能测评 (含答案)2025-2026学年数学苏科版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 247.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 14:43:02 | ||
图片预览

文档简介
对称图形——圆 素能测评
一、 选择题(每小题3分,共24分)
1.
在平面直角坐标系中,☉O的半径为5,圆心为坐标原点,则下列各点中,在☉O外的是 ( )
A. (2,4) B. (3,4) C. (4,3) D. (5,4)
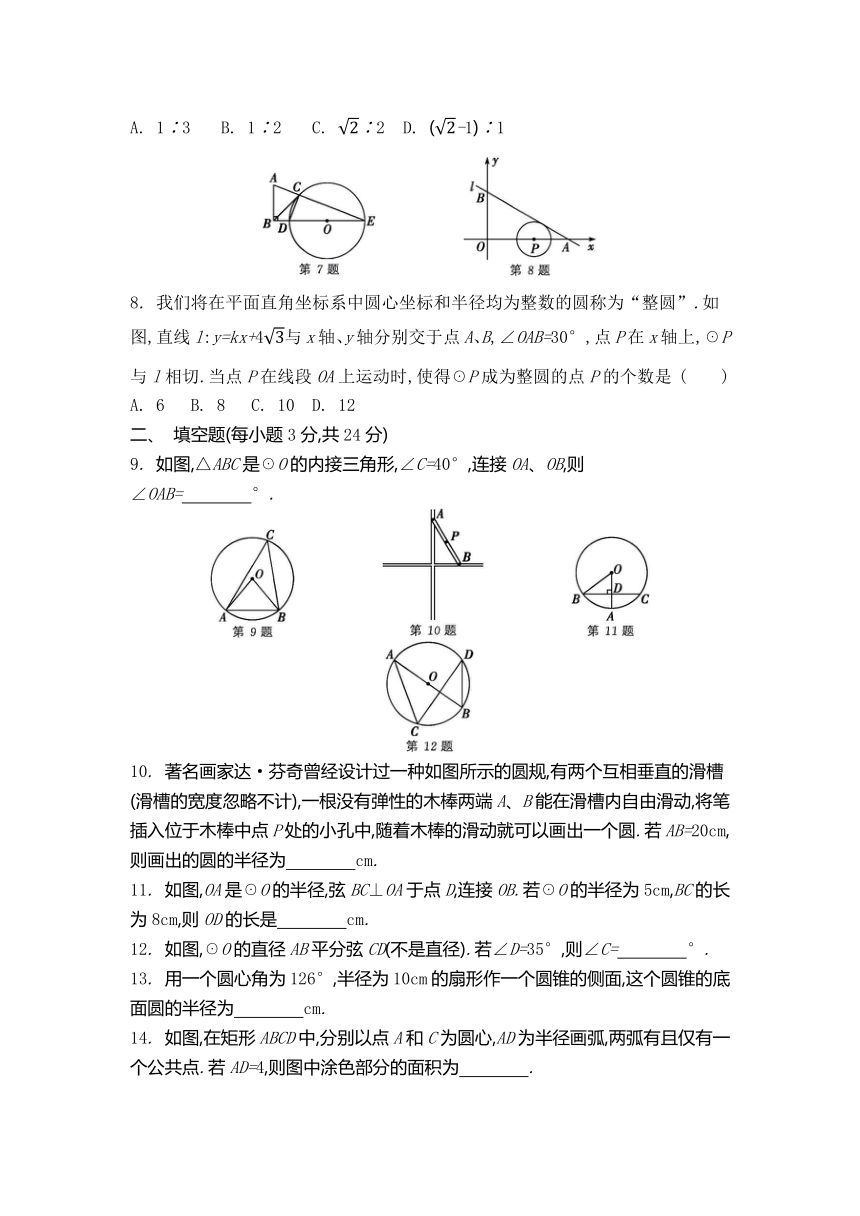
2. 如图,AD是☉O的直径,AB是☉O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是 ( )
A. 61° B. 63° C. 65° D. 67°
3. 如图,四边形ABCD内接于☉O,E为BC的延长线上的一点.若∠DCE=65°,则∠BOD的度数是 ( )
A. 65° B. 115° C. 130° D. 140°
4. 为筹备运动会,小松制作了如图所示的宣传牌,在正五边形ABCDE和正方形CDFG中,CF、DG的延长线分别交AE、AB于点M、N,则∠FME的度数是 ( )
A. 90° B. 99° C. 108° D. 135°
5. 如图,分别以等边三角形ABC的三个顶点为圆心,边长为半径作弧,三段圆弧围成的封闭图形称为“莱洛三角形”.若等边三角形ABC的边长为3,则该“莱洛三角形”的周长为 ( )
A. π B. 3π C. 2π D. 2π-
6. 直角三角形的两边长为6和8,则此三角形的外接圆半径为 ( )
A. 5 B. 4 C. 5或 D. 5或4
7. 如图,在△ABE中,∠ABE=90°,BC为☉O的切线,C为切点.若CA=CD,则△ABC和△CDE的面积之比为( )
A. 1∶3 B. 1∶2 C. ∶2 D. (-1)∶1
8. 我们将在平面直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4与x轴、y轴分别交于点A、B,∠OAB=30°,点P在x轴上,☉P与l相切.当点P在线段OA上运动时,使得☉P成为整圆的点P的个数是 ( )
A. 6 B. 8 C. 10 D. 12
二、 填空题(每小题3分,共24分)
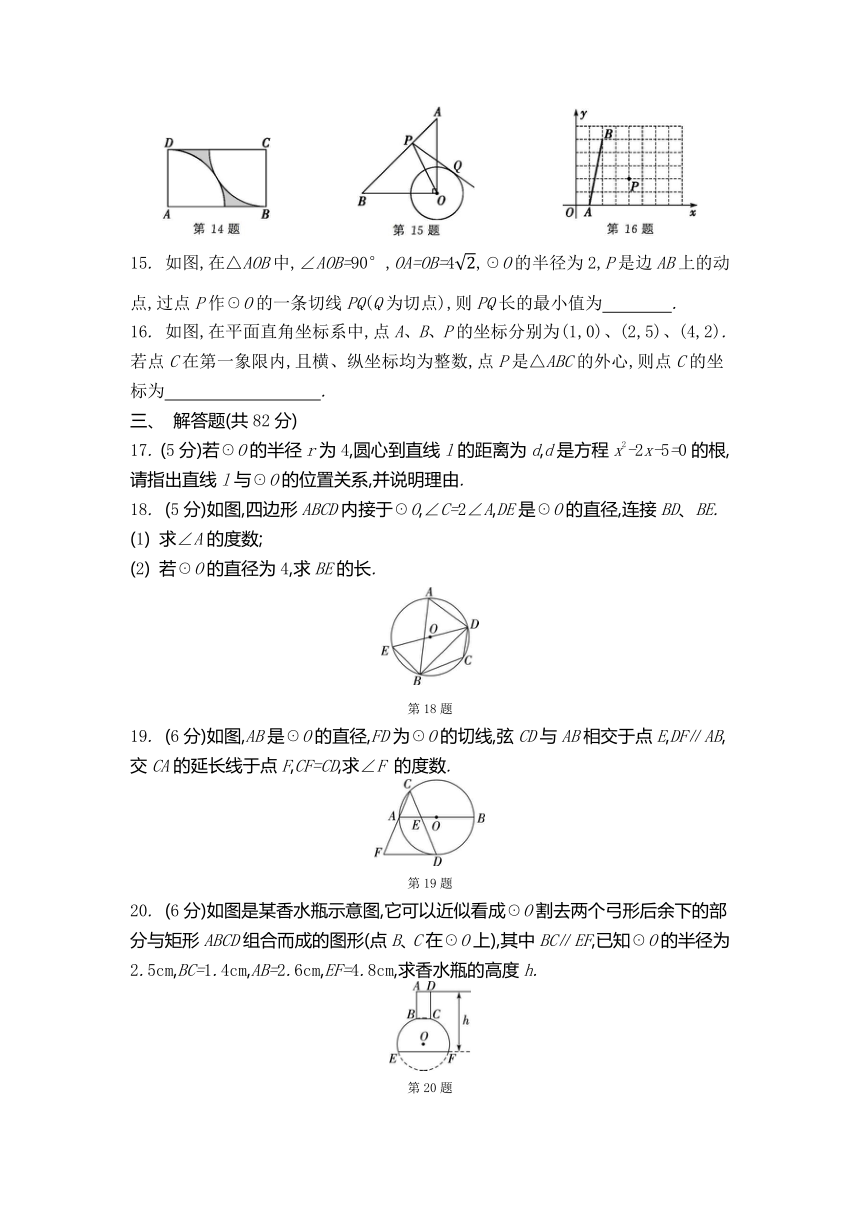
9. 如图,△ABC是☉O的内接三角形,∠C=40°,连接OA、OB,则∠OAB= °.
10. 著名画家达·芬奇曾经设计过一种如图所示的圆规,有两个互相垂直的滑槽(滑槽的宽度忽略不计),一根没有弹性的木棒两端A、B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆.若AB=20cm,则画出的圆的半径为 cm.
11. 如图,OA是☉O的半径,弦BC⊥OA于点D,连接OB.若☉O的半径为5cm,BC的长为8cm,则OD的长是 cm.
12. 如图,☉O的直径AB平分弦CD(不是直径).若∠D=35°,则∠C= °.
13. 用一个圆心角为126°,半径为10cm的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 cm.
14. 如图,在矩形ABCD中,分别以点A和C为圆心,AD为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中涂色部分的面积为 .
15. 如图,在△AOB中,∠AOB=90°,OA=OB=4,☉O的半径为2,P是边AB上的动点,过点P作☉O的一条切线PQ(Q为切点),则PQ长的最小值为 .
16. 如图,在平面直角坐标系中,点A、B、P的坐标分别为(1,0)、(2,5)、(4,2).若点C在第一象限内,且横、纵坐标均为整数,点P是△ABC的外心,则点C的坐标为 .
三、 解答题(共82分)
17. (5分)若☉O的半径r为4,圆心到直线l的距离为d,d是方程x2-2x-5=0的根,请指出直线l与☉O的位置关系,并说明理由.
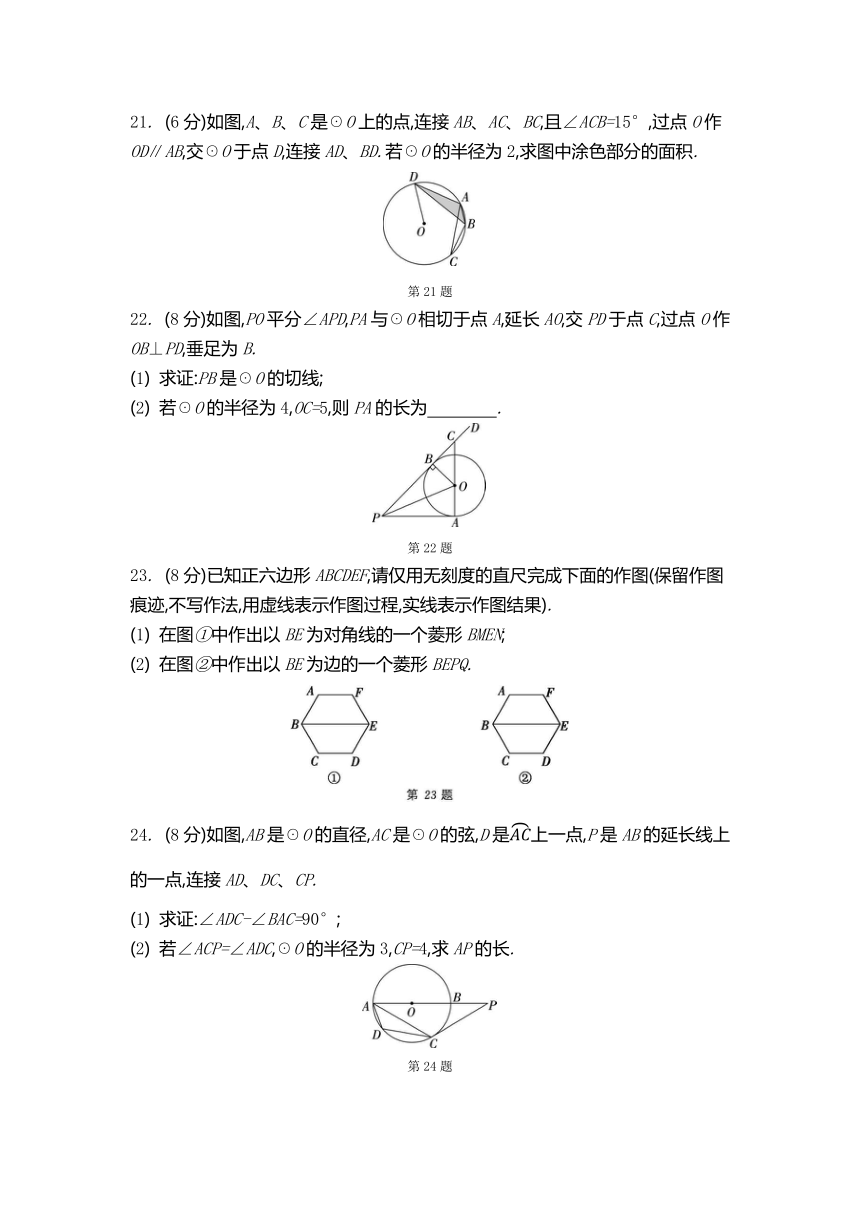
18. (5分)如图,四边形ABCD内接于☉O,∠C=2∠A,DE是☉O的直径,连接BD、BE.
(1) 求∠A的度数;
(2) 若☉O的直径为4,求BE的长.
第18题
19. (6分)如图,AB是☉O的直径,FD为☉O的切线,弦CD与AB相交于点E,DF∥AB,交CA的延长线于点F,CF=CD,求∠F 的度数.
第19题
20. (6分)如图是某香水瓶示意图,它可以近似看成☉O割去两个弓形后余下的部分与矩形ABCD组合而成的图形(点B、C在☉O上),其中BC∥EF,已知☉O的半径为2.5cm,BC=1.4cm,AB=2.6cm,EF=4.8cm,求香水瓶的高度h.
第20题
21. (6分)如图,A、B、C是☉O上的点,连接AB、AC、BC,且∠ACB=15°,过点O作OD∥AB,交☉O于点D,连接AD、BD.若☉O的半径为2,求图中涂色部分的面积.
第21题
22. (8分)如图,PO平分∠APD,PA与☉O相切于点A,延长AO,交PD于点C,过点O作OB⊥PD,垂足为B.
(1) 求证:PB是☉O的切线;
(2) 若☉O的半径为4,OC=5,则PA的长为 .
第22题
23. (8分)已知正六边形ABCDEF,请仅用无刻度的直尺完成下面的作图(保留作图痕迹,不写作法,用虚线表示作图过程,实线表示作图结果).
(1) 在图①中作出以BE为对角线的一个菱形BMEN;
(2) 在图②中作出以BE为边的一个菱形BEPQ.
24. (8分)如图,AB是☉O的直径,AC是☉O的弦,D是上一点,P是AB的延长线上的一点,连接AD、DC、CP.
(1) 求证:∠ADC-∠BAC=90°;
(2) 若∠ACP=∠ADC,☉O的半径为3,CP=4,求AP的长.
第24题
25. (10分)如图,在△ABC中,AB=AC,以AB为直径的☉O交边AC于点D,连接BD,过点C作CE∥AB.
(1) 请用无刻度的直尺和圆规作图:过点B作☉O的切线,交CE于点F(不写作法,保留作图痕迹,标明字母);
(2) 在(1)的条件下,求证:BD=BF.
第25题
26. (10分)如图,☉O的半径为5,B、C是☉O上两定点,A是☉O上一动点,且∠BAC=60°,∠BAC的平分线交☉O于点D.
(1) 求证:D为上一定点.
(2) 过点D作BC的平行线,交AB的延长线于点F.
① 判断DF与☉O的位置关系,并说明理由;
② 若△ABC为锐角三角形,则DF长的取值范围是 .
第26题
27. (10分)如图,点A的坐标为(5,0),点B的坐标为(3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(-4,0)出发,沿x轴向右以每秒2个单位长度的速度运动,运动时间为t秒.
(1) 求点C的坐标.
(2) 当点P在点B的左侧,且∠BCP=15°时,求t的值.
(3) 以点P为圆心、PC为半径的☉P随点P的运动而变化.若☉P与四边形ABCD的边(或边所在的直线)相切,则t的值为 .
第27题
第2章素能测评
一、 1. D 2. B 3. C 4. B 5. B 6. D
7. B 解析:连接OC.根据圆周角的性质与切线的性质,可以证明△ABC≌△COD,再由S△COD=S△COE=S△CDE,可得S△ABC=S△CDE,即△ABC和△CDE的面积之比为1∶2.
8. A
二、 9. 50 10. 10 11. 3 12. 55 13. 3.5 14. 16-8π 15. 2 16. (7,4)或(6,5)或(1,4)
三、 17. 直线l与☉O相交 理由:解方程x2-2x-5=0,得x1=1+,x2=1-(不合题意,舍去).∴ d=1+.∵ 2<<3,∴ 3<1+<4.∵ r=4,∴ d18. (1) ∵ 四边形ABCD内接于☉O,∴ ∠C+∠A=180°.∵ ∠C=2∠A,∴ ∠A=60° (2) ∵ DE是☉O的直径,∴ ∠DBE=90°.∵ =,∴ ∠E=∠A=60°,∴ 在Rt△EBD中,∠BDE=90°-60°=30°,∴ 易得BE=DE=×4=2
19. 连接OD.∵ FD为☉O的切线,∴ OD⊥DF,即∠ODF=90°.∵ DF∥AB,∴ ∠AOD+∠ODF=180°,∴ ∠AOD=90°.∵ =,∴ ∠ACD=∠AOD=45°.∵ CF=CD,∴ ∠F=∠CDF==67.5°
20. 如图,过点O作OM⊥BC于点M,延长MO,交EF于点N,连接OC、OF.∵ BC∥EF,OM⊥BC,∴ ON⊥EF,∴ CM=BC=×1.4=0.7(cm),NF=EF=×4.8=2.4(cm),∴ OM===2.4(cm),ON===0.7(cm),∴ 香水瓶的高度h=AB+OM+ON=2.6+2.4+0.7=5.7(cm)
21. 连接OA、OB.∵ =,∴ ∠AOB=2∠ACB=30°,∴ S扇形OAB==.∵ OD∥AB,∴ 易得S涂色部分=S扇形OAB=
22. (1) ∵ PA与☉O相切于点A,∴ OA⊥PA.∵ PO平分∠APD,OB⊥PD,∴ OB=OA,∴ PB是☉O的切线
(2) 12 解析:根据题意,得OA=OB=4.∵ OC=5,∴ AC=OA+OC=4+5=9.∵ OA⊥PA,OB⊥PD,∴ ∠PAO=∠PBO=∠OBC=90°,∴ 在Rt△OBC中,BC==3.在Rt△PAO和Rt△PBO中,∴ Rt△PAO≌Rt△PBO,∴ PA=PB.∵ 在Rt△PAC中,PA2+AC2=PC2,∴ PA2+92=(PA+3)2,解得PA=12,∴ PA的长是12.
23. 答案不唯一,如(1) 如图①,菱形BMEN即为所求作
(2) 如图②,菱形BEPQ即为所求作
24. (1) 连接BC.∵ AB是☉O的直径,∴ ∠ACB=90°.∵ ∠PBC=∠BAC+∠ACB,∴ ∠PBC-∠BAC=90°.∵ 四边形ABCD为☉O的内接四边形,∴ ∠ADC+∠ABC=180°.∵ ∠PBC+∠ABC=180°,∴ ∠ADC=∠PBC,∴ ∠ADC-∠BAC=90° (2) 连接OC.∵ ∠ACP=∠ADC,∠ADC-∠BAC=90°,∴ ∠ACP-∠BAC=90°.∵ OA=OC,∴ ∠BAC=∠ACO,∴ ∠ACP-∠ACO=90°,即∠OCP=90°,∴ 在Rt△OCP中,OC2+CP2=OP2.∵ ☉O的半径为3,CP=4,∴ OP==5,OA=3,∴ AP=OP+OA=8
25. (1) 如图 (2) ∵ AB=AC,∴ ∠ABC=∠ACB.∵ AB∥CE,∴ ∠ABC=∠BCF,∠BFC+∠ABF=180°,∴ ∠BCF=∠ACB.∵ AB为☉O的直径,∴ ∠ADB=90°.∵ ∠ADB+∠BDC=180°,∴ ∠BDC=90°.∵ BF为☉O的切线,∴ ∠ABF=90°,∴ ∠BFC=90°,∴ ∠BDC=∠BFC.在△BCD和△BCF中,∴ △BCD≌△BCF,∴ BD=BF
26. (1) 如图,连接OB、OD.∵ ∠BAC=60°,∠BAC的平分线交☉O于点D,∴ ∠BAD=∠BAC=30°.∵ =,∴ ∠BOD=2∠BAD=60°,∴ 的度数是60°(定值).∵ B为定点,∴ D为上一定点 (2) ① DF与☉O相切 理由:如图,连接OC.设OD与BC交于点E.∵ ∠BAC的平分线交☉O于点D,∴ ∠BAD=∠CAD,∴ =,∴ ∠BOD=∠COD.∵ OB=OC,∴ OD⊥BC,∴ ∠OEB=90°.∵ DF∥BC,∴ ∠FDO=∠OEB=90°,∴ OD⊥DF.∵ OD为☉O的半径,∴ DF与☉O相切.
②27. (1) ∵ A、B两点的坐标分别为(5,0)、(3,0),∴ OA=5,OB=3.∵ 在Rt△COB中,∠CBO=45°,∴ ∠OCB=180°-90°-45°=45°=∠CBO,∴ OC=OB=3,∴ 点C的坐标为(0,3) (2) 当点P在点B的左侧时,∠OCB=45°,∠BCP=15°,∴ ∠OCP=∠OCB-∠BCP=45°-15°=30°,∴ 在Rt△POC中,易得OP=CP.∵ OC=3,∴ OP2+32=(2OP)2,∴ OP=.∵ 点Q的坐标为(-4,0),∴ OQ=4,∴ QP=+4.∵ 点P从点Q出发,沿x轴向右以每秒2个单位长度的速度运动,∴ t=
(3) 或2或 解析:分☉P与BC相切、☉P与CD相切、☉P与AD相切三种情况讨论.
一、 选择题(每小题3分,共24分)
1.
在平面直角坐标系中,☉O的半径为5,圆心为坐标原点,则下列各点中,在☉O外的是 ( )
A. (2,4) B. (3,4) C. (4,3) D. (5,4)
2. 如图,AD是☉O的直径,AB是☉O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是 ( )
A. 61° B. 63° C. 65° D. 67°
3. 如图,四边形ABCD内接于☉O,E为BC的延长线上的一点.若∠DCE=65°,则∠BOD的度数是 ( )
A. 65° B. 115° C. 130° D. 140°
4. 为筹备运动会,小松制作了如图所示的宣传牌,在正五边形ABCDE和正方形CDFG中,CF、DG的延长线分别交AE、AB于点M、N,则∠FME的度数是 ( )
A. 90° B. 99° C. 108° D. 135°
5. 如图,分别以等边三角形ABC的三个顶点为圆心,边长为半径作弧,三段圆弧围成的封闭图形称为“莱洛三角形”.若等边三角形ABC的边长为3,则该“莱洛三角形”的周长为 ( )
A. π B. 3π C. 2π D. 2π-
6. 直角三角形的两边长为6和8,则此三角形的外接圆半径为 ( )
A. 5 B. 4 C. 5或 D. 5或4
7. 如图,在△ABE中,∠ABE=90°,BC为☉O的切线,C为切点.若CA=CD,则△ABC和△CDE的面积之比为( )
A. 1∶3 B. 1∶2 C. ∶2 D. (-1)∶1
8. 我们将在平面直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4与x轴、y轴分别交于点A、B,∠OAB=30°,点P在x轴上,☉P与l相切.当点P在线段OA上运动时,使得☉P成为整圆的点P的个数是 ( )
A. 6 B. 8 C. 10 D. 12
二、 填空题(每小题3分,共24分)
9. 如图,△ABC是☉O的内接三角形,∠C=40°,连接OA、OB,则∠OAB= °.
10. 著名画家达·芬奇曾经设计过一种如图所示的圆规,有两个互相垂直的滑槽(滑槽的宽度忽略不计),一根没有弹性的木棒两端A、B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆.若AB=20cm,则画出的圆的半径为 cm.
11. 如图,OA是☉O的半径,弦BC⊥OA于点D,连接OB.若☉O的半径为5cm,BC的长为8cm,则OD的长是 cm.
12. 如图,☉O的直径AB平分弦CD(不是直径).若∠D=35°,则∠C= °.
13. 用一个圆心角为126°,半径为10cm的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 cm.
14. 如图,在矩形ABCD中,分别以点A和C为圆心,AD为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中涂色部分的面积为 .
15. 如图,在△AOB中,∠AOB=90°,OA=OB=4,☉O的半径为2,P是边AB上的动点,过点P作☉O的一条切线PQ(Q为切点),则PQ长的最小值为 .
16. 如图,在平面直角坐标系中,点A、B、P的坐标分别为(1,0)、(2,5)、(4,2).若点C在第一象限内,且横、纵坐标均为整数,点P是△ABC的外心,则点C的坐标为 .
三、 解答题(共82分)
17. (5分)若☉O的半径r为4,圆心到直线l的距离为d,d是方程x2-2x-5=0的根,请指出直线l与☉O的位置关系,并说明理由.
18. (5分)如图,四边形ABCD内接于☉O,∠C=2∠A,DE是☉O的直径,连接BD、BE.
(1) 求∠A的度数;
(2) 若☉O的直径为4,求BE的长.
第18题
19. (6分)如图,AB是☉O的直径,FD为☉O的切线,弦CD与AB相交于点E,DF∥AB,交CA的延长线于点F,CF=CD,求∠F 的度数.
第19题
20. (6分)如图是某香水瓶示意图,它可以近似看成☉O割去两个弓形后余下的部分与矩形ABCD组合而成的图形(点B、C在☉O上),其中BC∥EF,已知☉O的半径为2.5cm,BC=1.4cm,AB=2.6cm,EF=4.8cm,求香水瓶的高度h.
第20题
21. (6分)如图,A、B、C是☉O上的点,连接AB、AC、BC,且∠ACB=15°,过点O作OD∥AB,交☉O于点D,连接AD、BD.若☉O的半径为2,求图中涂色部分的面积.
第21题
22. (8分)如图,PO平分∠APD,PA与☉O相切于点A,延长AO,交PD于点C,过点O作OB⊥PD,垂足为B.
(1) 求证:PB是☉O的切线;
(2) 若☉O的半径为4,OC=5,则PA的长为 .
第22题
23. (8分)已知正六边形ABCDEF,请仅用无刻度的直尺完成下面的作图(保留作图痕迹,不写作法,用虚线表示作图过程,实线表示作图结果).
(1) 在图①中作出以BE为对角线的一个菱形BMEN;
(2) 在图②中作出以BE为边的一个菱形BEPQ.
24. (8分)如图,AB是☉O的直径,AC是☉O的弦,D是上一点,P是AB的延长线上的一点,连接AD、DC、CP.
(1) 求证:∠ADC-∠BAC=90°;
(2) 若∠ACP=∠ADC,☉O的半径为3,CP=4,求AP的长.
第24题
25. (10分)如图,在△ABC中,AB=AC,以AB为直径的☉O交边AC于点D,连接BD,过点C作CE∥AB.
(1) 请用无刻度的直尺和圆规作图:过点B作☉O的切线,交CE于点F(不写作法,保留作图痕迹,标明字母);
(2) 在(1)的条件下,求证:BD=BF.
第25题
26. (10分)如图,☉O的半径为5,B、C是☉O上两定点,A是☉O上一动点,且∠BAC=60°,∠BAC的平分线交☉O于点D.
(1) 求证:D为上一定点.
(2) 过点D作BC的平行线,交AB的延长线于点F.
① 判断DF与☉O的位置关系,并说明理由;
② 若△ABC为锐角三角形,则DF长的取值范围是 .
第26题
27. (10分)如图,点A的坐标为(5,0),点B的坐标为(3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(-4,0)出发,沿x轴向右以每秒2个单位长度的速度运动,运动时间为t秒.
(1) 求点C的坐标.
(2) 当点P在点B的左侧,且∠BCP=15°时,求t的值.
(3) 以点P为圆心、PC为半径的☉P随点P的运动而变化.若☉P与四边形ABCD的边(或边所在的直线)相切,则t的值为 .
第27题
第2章素能测评
一、 1. D 2. B 3. C 4. B 5. B 6. D
7. B 解析:连接OC.根据圆周角的性质与切线的性质,可以证明△ABC≌△COD,再由S△COD=S△COE=S△CDE,可得S△ABC=S△CDE,即△ABC和△CDE的面积之比为1∶2.
8. A
二、 9. 50 10. 10 11. 3 12. 55 13. 3.5 14. 16-8π 15. 2 16. (7,4)或(6,5)或(1,4)
三、 17. 直线l与☉O相交 理由:解方程x2-2x-5=0,得x1=1+,x2=1-(不合题意,舍去).∴ d=1+.∵ 2<<3,∴ 3<1+<4.∵ r=4,∴ d
19. 连接OD.∵ FD为☉O的切线,∴ OD⊥DF,即∠ODF=90°.∵ DF∥AB,∴ ∠AOD+∠ODF=180°,∴ ∠AOD=90°.∵ =,∴ ∠ACD=∠AOD=45°.∵ CF=CD,∴ ∠F=∠CDF==67.5°
20. 如图,过点O作OM⊥BC于点M,延长MO,交EF于点N,连接OC、OF.∵ BC∥EF,OM⊥BC,∴ ON⊥EF,∴ CM=BC=×1.4=0.7(cm),NF=EF=×4.8=2.4(cm),∴ OM===2.4(cm),ON===0.7(cm),∴ 香水瓶的高度h=AB+OM+ON=2.6+2.4+0.7=5.7(cm)
21. 连接OA、OB.∵ =,∴ ∠AOB=2∠ACB=30°,∴ S扇形OAB==.∵ OD∥AB,∴ 易得S涂色部分=S扇形OAB=
22. (1) ∵ PA与☉O相切于点A,∴ OA⊥PA.∵ PO平分∠APD,OB⊥PD,∴ OB=OA,∴ PB是☉O的切线
(2) 12 解析:根据题意,得OA=OB=4.∵ OC=5,∴ AC=OA+OC=4+5=9.∵ OA⊥PA,OB⊥PD,∴ ∠PAO=∠PBO=∠OBC=90°,∴ 在Rt△OBC中,BC==3.在Rt△PAO和Rt△PBO中,∴ Rt△PAO≌Rt△PBO,∴ PA=PB.∵ 在Rt△PAC中,PA2+AC2=PC2,∴ PA2+92=(PA+3)2,解得PA=12,∴ PA的长是12.
23. 答案不唯一,如(1) 如图①,菱形BMEN即为所求作
(2) 如图②,菱形BEPQ即为所求作
24. (1) 连接BC.∵ AB是☉O的直径,∴ ∠ACB=90°.∵ ∠PBC=∠BAC+∠ACB,∴ ∠PBC-∠BAC=90°.∵ 四边形ABCD为☉O的内接四边形,∴ ∠ADC+∠ABC=180°.∵ ∠PBC+∠ABC=180°,∴ ∠ADC=∠PBC,∴ ∠ADC-∠BAC=90° (2) 连接OC.∵ ∠ACP=∠ADC,∠ADC-∠BAC=90°,∴ ∠ACP-∠BAC=90°.∵ OA=OC,∴ ∠BAC=∠ACO,∴ ∠ACP-∠ACO=90°,即∠OCP=90°,∴ 在Rt△OCP中,OC2+CP2=OP2.∵ ☉O的半径为3,CP=4,∴ OP==5,OA=3,∴ AP=OP+OA=8
25. (1) 如图 (2) ∵ AB=AC,∴ ∠ABC=∠ACB.∵ AB∥CE,∴ ∠ABC=∠BCF,∠BFC+∠ABF=180°,∴ ∠BCF=∠ACB.∵ AB为☉O的直径,∴ ∠ADB=90°.∵ ∠ADB+∠BDC=180°,∴ ∠BDC=90°.∵ BF为☉O的切线,∴ ∠ABF=90°,∴ ∠BFC=90°,∴ ∠BDC=∠BFC.在△BCD和△BCF中,∴ △BCD≌△BCF,∴ BD=BF
26. (1) 如图,连接OB、OD.∵ ∠BAC=60°,∠BAC的平分线交☉O于点D,∴ ∠BAD=∠BAC=30°.∵ =,∴ ∠BOD=2∠BAD=60°,∴ 的度数是60°(定值).∵ B为定点,∴ D为上一定点 (2) ① DF与☉O相切 理由:如图,连接OC.设OD与BC交于点E.∵ ∠BAC的平分线交☉O于点D,∴ ∠BAD=∠CAD,∴ =,∴ ∠BOD=∠COD.∵ OB=OC,∴ OD⊥BC,∴ ∠OEB=90°.∵ DF∥BC,∴ ∠FDO=∠OEB=90°,∴ OD⊥DF.∵ OD为☉O的半径,∴ DF与☉O相切.
②
(3) 或2或 解析:分☉P与BC相切、☉P与CD相切、☉P与AD相切三种情况讨论.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
