第4章等可能条件下的概率 整合提升(含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 第4章等可能条件下的概率 整合提升(含答案) 2025-2026学年数学苏科版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 108.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 00:00:00 | ||
图片预览


文档简介
第4章 等可能条件下的概率 整合提升
考点一 用概率公式求概率
1.
(2023·泸州)从1、2、3、4、5、5六个数中随机选取一个数,这个数恰为该组数据的众数的概率为 ( )
A. B. C. D.
第2题
2. (2024·太仓期中)如图,一块飞镖游戏板由除颜色外都相同的9个小正方形构成.假设飞镖击中每1块小正方形是等可能的(击中小正方形的边界或没有击中游戏板,则重投一次).任意投掷飞镖一次,击中灰色区域的概率是 ( )
A. B. C. D.
3. (新考向·传统文化)(2024·湖北)小亮了解了祖冲之、刘徽、赵爽、杨辉、秦九韶这5位著名数学家的生平简介,知晓他们取得的伟大成就对我国乃至世界数学发展起到的巨大推进作用,准备在数学课上随机选取其中一位的成就进行分享,选到数学家赵爽的概率是 .
4. (2023·新疆)在平面直角坐标系中有五个点,分别是A(1,2)、B(-3,4)、C(-2,-3)、D(4,3)、E(2,-3),从中任选一个点恰好在第一象限的概率是 .
5. 一个不透明的袋中装有5个黄球、13个黑球和22个红球,它们除颜色外其他都相同.
(1) 求从袋中摸出1个球是黄球的概率;
(2) 现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,从袋中摸出1个球是黄球的概率不小于,则至少取出了多少个黑球
考点二 用画树状图或列表的方法求概率
6. (2024·大庆)“铁人王进喜纪念馆”“龙凤湿地公园”“滨水绿道”和“数字大庆中心”是大庆市四个有代表性的旅游景点.若小娜从这四个景点中随机选择两个景点游览,则这两个景点中有“铁人王进喜纪念馆”的概率是 ( )
A. B. C. D.
7. (2024·德州)衣橱里挂着3套不同颜色的服装,同一套服装的上衣与裤子的颜色相同,若从衣橱里各任取一件上衣和一条裤子,则它们取自同一套的概率是 .
8. (2023·伊春)已知一个不透明的袋子中装有3个红球和2个白球,这些小球除标号外完全相同,随机摸出两个小球,恰好是一红一白的概率为 .
9. (2024·苏州)一个不透明的盒子里装有4张书签,分别描绘“春”“夏”“秋”“冬”四个季节,书签除图案外都相同,并将4张书签充分搅匀.
(1) 若从盒子中任意抽取1张书签,恰好抽到“夏”的概率为 ;
(2) 若从盒子中任意抽取2张书签(先抽取1张书签,且这张书签不放回,再抽取1张书签),求抽取的书签恰好1张为“春”,1张为“秋”的概率(请用画树状图或列表的方法求解).
10. (2023·常州)在5张相同的小纸条上,分别写有:① ;② ;③ 1;④ 乘法;⑤ 加法.将这5张小纸条做成5支签,①②③放在不透明的盒子A中搅匀,④⑤放在不透明的盒子B中搅匀.
(1) 从盒子A中任意抽出1支签,抽到无理数的概率是 .
(2) 先从盒子A中任意抽出2支签,再从盒子B中任意抽出1支签.求抽到的2个实数进行相应的运算后结果是无理数的概率.
第11题
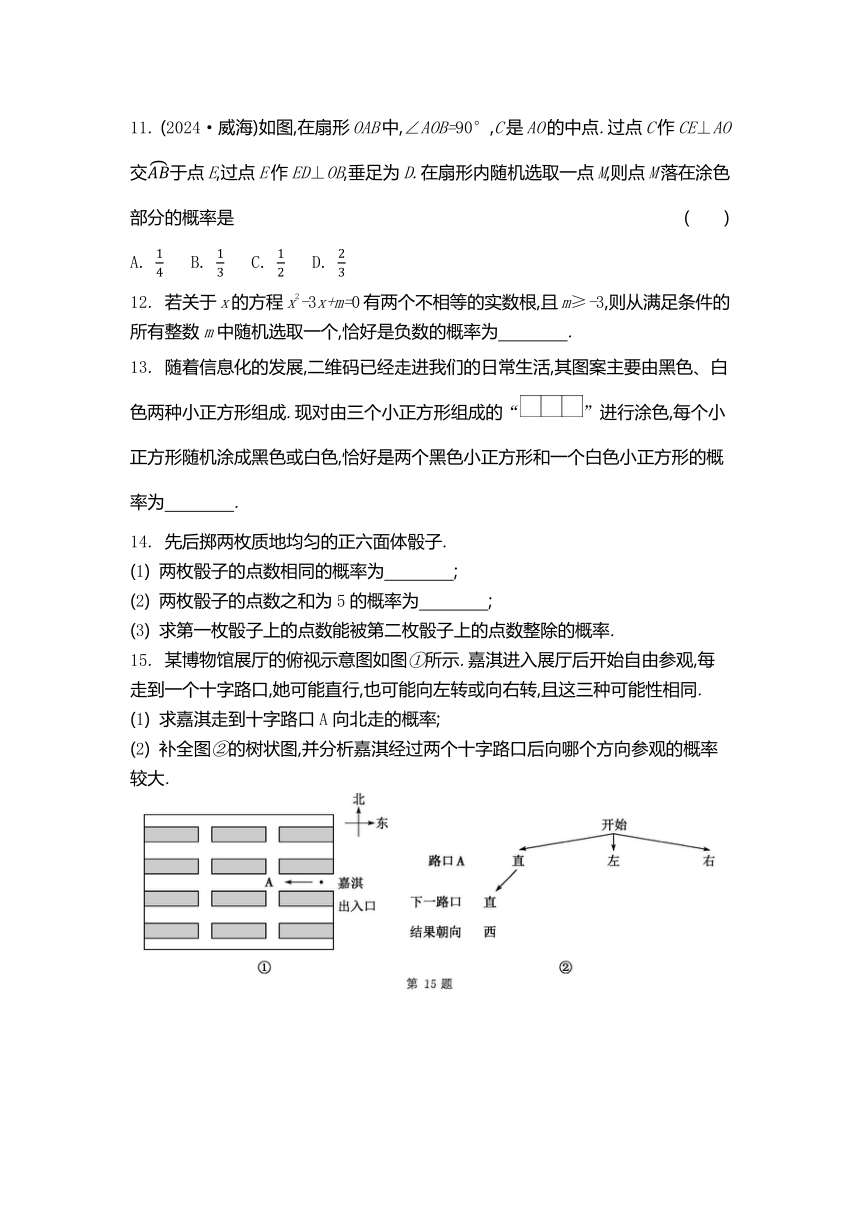
11. (2024·威海)如图,在扇形OAB中,∠AOB=90°,C是AO的中点.过点C作CE⊥AO交于点E,过点E作ED⊥OB,垂足为D.在扇形内随机选取一点M,则点M落在涂色部分的概率是 ( )
A. B. C. D.
12. 若关于x的方程x2-3x+m=0有两个不相等的实数根,且m≥-3,则从满足条件的所有整数m中随机选取一个,恰好是负数的概率为 .
13. 随着信息化的发展,二维码已经走进我们的日常生活,其图案主要由黑色、白色两种小正方形组成.现对由三个小正方形组成的“”进行涂色,每个小正方形随机涂成黑色或白色,恰好是两个黑色小正方形和一个白色小正方形的概率为 .
14. 先后掷两枚质地均匀的正六面体骰子.
(1) 两枚骰子的点数相同的概率为 ;
(2) 两枚骰子的点数之和为5的概率为 ;
(3) 求第一枚骰子上的点数能被第二枚骰子上的点数整除的概率.
15. 某博物馆展厅的俯视示意图如图①所示.嘉淇进入展厅后开始自由参观,每走到一个十字路口,她可能直行,也可能向左转或向右转,且这三种可能性相同.
(1) 求嘉淇走到十字路口A向北走的概率;
(2) 补全图②的树状图,并分析嘉淇经过两个十字路口后向哪个方向参观的概率较大.
第4章 等可能条件下的概率 整合提升
1. B 2. C 3. 4.
5. (1) P(摸出1个球是黄球)== (2) 设取出了x个黑球.根据题意,得≥,解得x≥.∴ x的最小正整数值是9,∴ 至少取出了9个黑球
6. D 7. 8.
9. (1) (2) 列表如下:
第2张 第1张 春 夏 秋 冬
春 (春,夏) (春,秋) (春,冬)
夏 (夏,春) (夏,秋) (夏,冬)
秋 (秋,春) (秋,夏) (秋,冬)
冬 (冬,春) (冬,夏) (冬,秋)
由表格,可知从盒子中任意抽取2张书签共有12种等可能的结果,其中抽取的书签恰好1张为“春”,1张为“秋”的结果有2种,∴ P(抽取的书签恰好1张为“春”,1张为“秋”)==
10. (1) (2) 画树状图如图所示.由树状图,可知先从盒子A中任意抽出2支签,再从盒子B中任意抽出1支签共有12种等可能的结果,其中抽到的2个实数进行相应的运算后结果是无理数的有①②⑤,①③④,①③⑤,②①⑤,②③④,②③⑤,③①④,③①⑤,③②④,③②⑤,共10种,∴ P(抽到的2个实数进行相应的运算后结果是无理数)==
11. B 解析:设扇形的半径为r.∵ CE⊥AO,∴ ∠OCE=90°.∵ C是AO的中点,∴ OC=OA=OE.取OE的中点F,连接CF.∴ 在Rt△OCE中,CF=OE=OF,∴ OC=CF=OF,∴ △OCF是等边三角形,∴ ∠COE=60°.∵ ∠AOB=90°,∴ ∠BOE=∠AOB-∠COE=30°.∵ ED⊥OB,∴ ∠ODE=90°,∴ 四边形OCED为矩形,∴ S△OCE=S△ODE,∴ S涂色部分=S扇形OBE=.∵ S扇形OAB=,∴ P(点M落在涂色部分)==.
12. 解析:∵ 关于x的方程x2-3x+m=0有两个不相等的实数根,∴ (-3)2-4×1×m>0,解得m<.又∵ m≥-3,∴ -3≤m<,∴ 满足条件的所有整数为-3、-2、-1、0、1、2,共6个,其中负数为-3、-2、-1,共3个,∴ 从满足条件的所有整数m中随机选取一个,恰好是负数的概率为=.
13.
14. (1) (2) (3) 列表如下:
第二枚 第一枚 1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
由表格,可知共有36种等可能的结果,其中(1,1)、(2,1)、(3,1)、(4,1)、(5,1)、(6,1)、(2,2)、(4,2)、(6,2)、(3,3)、(6,3)、(4,4)、(5,5)、(6,6)这14种结果满足第一枚骰子上的点数能被第二枚骰子上的点数整除,∴ P(第一枚骰子上的点数能被第二枚骰子上的点数整除)==
15. (1) ∵ 当嘉淇走到十字路口A时,有直行、向左转、向右转3种等可能的走向,其中只有向右转为向北走,∴ P(向北走)= (2) 补全树状图如图所示.由树状图,可知嘉淇经过两个十字路口后的走向共有9种等可能的结果,其中向西参观的结果有3种,向南参观的结果有2种,向北参观的结果有2种,向东参观的结果有2种,∴ P(向西参观)==,P(向南参观)=P(向北参观)=P(向东参观)=.∵ >,∴ 嘉淇经过两个十字路口后向西参观的概率较大
考点一 用概率公式求概率
1.
(2023·泸州)从1、2、3、4、5、5六个数中随机选取一个数,这个数恰为该组数据的众数的概率为 ( )
A. B. C. D.
第2题
2. (2024·太仓期中)如图,一块飞镖游戏板由除颜色外都相同的9个小正方形构成.假设飞镖击中每1块小正方形是等可能的(击中小正方形的边界或没有击中游戏板,则重投一次).任意投掷飞镖一次,击中灰色区域的概率是 ( )
A. B. C. D.
3. (新考向·传统文化)(2024·湖北)小亮了解了祖冲之、刘徽、赵爽、杨辉、秦九韶这5位著名数学家的生平简介,知晓他们取得的伟大成就对我国乃至世界数学发展起到的巨大推进作用,准备在数学课上随机选取其中一位的成就进行分享,选到数学家赵爽的概率是 .
4. (2023·新疆)在平面直角坐标系中有五个点,分别是A(1,2)、B(-3,4)、C(-2,-3)、D(4,3)、E(2,-3),从中任选一个点恰好在第一象限的概率是 .
5. 一个不透明的袋中装有5个黄球、13个黑球和22个红球,它们除颜色外其他都相同.
(1) 求从袋中摸出1个球是黄球的概率;
(2) 现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,从袋中摸出1个球是黄球的概率不小于,则至少取出了多少个黑球
考点二 用画树状图或列表的方法求概率
6. (2024·大庆)“铁人王进喜纪念馆”“龙凤湿地公园”“滨水绿道”和“数字大庆中心”是大庆市四个有代表性的旅游景点.若小娜从这四个景点中随机选择两个景点游览,则这两个景点中有“铁人王进喜纪念馆”的概率是 ( )
A. B. C. D.
7. (2024·德州)衣橱里挂着3套不同颜色的服装,同一套服装的上衣与裤子的颜色相同,若从衣橱里各任取一件上衣和一条裤子,则它们取自同一套的概率是 .
8. (2023·伊春)已知一个不透明的袋子中装有3个红球和2个白球,这些小球除标号外完全相同,随机摸出两个小球,恰好是一红一白的概率为 .
9. (2024·苏州)一个不透明的盒子里装有4张书签,分别描绘“春”“夏”“秋”“冬”四个季节,书签除图案外都相同,并将4张书签充分搅匀.
(1) 若从盒子中任意抽取1张书签,恰好抽到“夏”的概率为 ;
(2) 若从盒子中任意抽取2张书签(先抽取1张书签,且这张书签不放回,再抽取1张书签),求抽取的书签恰好1张为“春”,1张为“秋”的概率(请用画树状图或列表的方法求解).
10. (2023·常州)在5张相同的小纸条上,分别写有:① ;② ;③ 1;④ 乘法;⑤ 加法.将这5张小纸条做成5支签,①②③放在不透明的盒子A中搅匀,④⑤放在不透明的盒子B中搅匀.
(1) 从盒子A中任意抽出1支签,抽到无理数的概率是 .
(2) 先从盒子A中任意抽出2支签,再从盒子B中任意抽出1支签.求抽到的2个实数进行相应的运算后结果是无理数的概率.
第11题
11. (2024·威海)如图,在扇形OAB中,∠AOB=90°,C是AO的中点.过点C作CE⊥AO交于点E,过点E作ED⊥OB,垂足为D.在扇形内随机选取一点M,则点M落在涂色部分的概率是 ( )
A. B. C. D.
12. 若关于x的方程x2-3x+m=0有两个不相等的实数根,且m≥-3,则从满足条件的所有整数m中随机选取一个,恰好是负数的概率为 .
13. 随着信息化的发展,二维码已经走进我们的日常生活,其图案主要由黑色、白色两种小正方形组成.现对由三个小正方形组成的“”进行涂色,每个小正方形随机涂成黑色或白色,恰好是两个黑色小正方形和一个白色小正方形的概率为 .
14. 先后掷两枚质地均匀的正六面体骰子.
(1) 两枚骰子的点数相同的概率为 ;
(2) 两枚骰子的点数之和为5的概率为 ;
(3) 求第一枚骰子上的点数能被第二枚骰子上的点数整除的概率.
15. 某博物馆展厅的俯视示意图如图①所示.嘉淇进入展厅后开始自由参观,每走到一个十字路口,她可能直行,也可能向左转或向右转,且这三种可能性相同.
(1) 求嘉淇走到十字路口A向北走的概率;
(2) 补全图②的树状图,并分析嘉淇经过两个十字路口后向哪个方向参观的概率较大.
第4章 等可能条件下的概率 整合提升
1. B 2. C 3. 4.
5. (1) P(摸出1个球是黄球)== (2) 设取出了x个黑球.根据题意,得≥,解得x≥.∴ x的最小正整数值是9,∴ 至少取出了9个黑球
6. D 7. 8.
9. (1) (2) 列表如下:
第2张 第1张 春 夏 秋 冬
春 (春,夏) (春,秋) (春,冬)
夏 (夏,春) (夏,秋) (夏,冬)
秋 (秋,春) (秋,夏) (秋,冬)
冬 (冬,春) (冬,夏) (冬,秋)
由表格,可知从盒子中任意抽取2张书签共有12种等可能的结果,其中抽取的书签恰好1张为“春”,1张为“秋”的结果有2种,∴ P(抽取的书签恰好1张为“春”,1张为“秋”)==
10. (1) (2) 画树状图如图所示.由树状图,可知先从盒子A中任意抽出2支签,再从盒子B中任意抽出1支签共有12种等可能的结果,其中抽到的2个实数进行相应的运算后结果是无理数的有①②⑤,①③④,①③⑤,②①⑤,②③④,②③⑤,③①④,③①⑤,③②④,③②⑤,共10种,∴ P(抽到的2个实数进行相应的运算后结果是无理数)==
11. B 解析:设扇形的半径为r.∵ CE⊥AO,∴ ∠OCE=90°.∵ C是AO的中点,∴ OC=OA=OE.取OE的中点F,连接CF.∴ 在Rt△OCE中,CF=OE=OF,∴ OC=CF=OF,∴ △OCF是等边三角形,∴ ∠COE=60°.∵ ∠AOB=90°,∴ ∠BOE=∠AOB-∠COE=30°.∵ ED⊥OB,∴ ∠ODE=90°,∴ 四边形OCED为矩形,∴ S△OCE=S△ODE,∴ S涂色部分=S扇形OBE=.∵ S扇形OAB=,∴ P(点M落在涂色部分)==.
12. 解析:∵ 关于x的方程x2-3x+m=0有两个不相等的实数根,∴ (-3)2-4×1×m>0,解得m<.又∵ m≥-3,∴ -3≤m<,∴ 满足条件的所有整数为-3、-2、-1、0、1、2,共6个,其中负数为-3、-2、-1,共3个,∴ 从满足条件的所有整数m中随机选取一个,恰好是负数的概率为=.
13.
14. (1) (2) (3) 列表如下:
第二枚 第一枚 1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
由表格,可知共有36种等可能的结果,其中(1,1)、(2,1)、(3,1)、(4,1)、(5,1)、(6,1)、(2,2)、(4,2)、(6,2)、(3,3)、(6,3)、(4,4)、(5,5)、(6,6)这14种结果满足第一枚骰子上的点数能被第二枚骰子上的点数整除,∴ P(第一枚骰子上的点数能被第二枚骰子上的点数整除)==
15. (1) ∵ 当嘉淇走到十字路口A时,有直行、向左转、向右转3种等可能的走向,其中只有向右转为向北走,∴ P(向北走)= (2) 补全树状图如图所示.由树状图,可知嘉淇经过两个十字路口后的走向共有9种等可能的结果,其中向西参观的结果有3种,向南参观的结果有2种,向北参观的结果有2种,向东参观的结果有2种,∴ P(向西参观)==,P(向南参观)=P(向北参观)=P(向东参观)=.∵ >,∴ 嘉淇经过两个十字路口后向西参观的概率较大
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
