期末素能测评 (含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 期末素能测评 (含答案) 2025-2026学年数学苏科版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 350.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 16:38:29 | ||
图片预览

文档简介
期末素能测评
一、 选择题(每小题3分,共24分)
1.
有一组数据:31、32、35、37、35.这组数据的平均数和中位数分别是 ( )
A. 34、34 B. 35、35
C. 34、35 D. 35、34
2. 不透明袋子中装有白球2个,红球1个,这些球除了颜色外无其他差别.从袋子中随机取出1个球,取出白球的概率是 ( )
A. 1 B. C. D.
3. 关于x的一元二次方程2x2-3x+k=0有实数根,则实数k的取值范围是 ( )
A. k< B. k≤ C. k≥ D. k<-
4. 某年级举办篮球友谊赛,参赛的每两个球队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队个数是 ( )
A. 6 B. 7 C. 8 D. 9
5. 若圆锥侧面展开图的面积是15π,母线长是5,则这个圆锥的底面圆的半径是 ( )
A. 3 B. 4 C. 5 D. 6
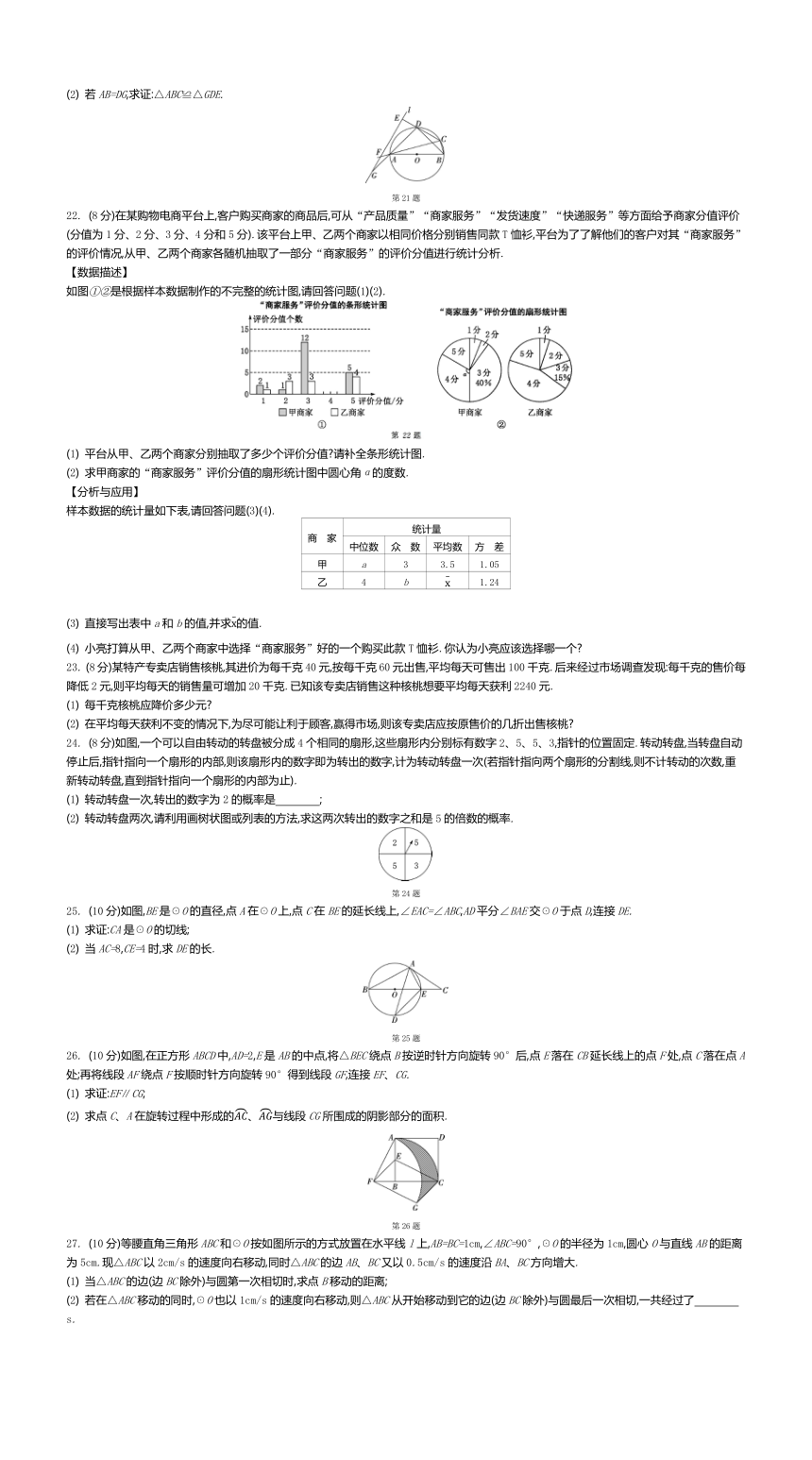
6. 如图,分别延长圆内接四边形ABCD的两组对边,延长线相交于点E、F.若∠E=54°41',∠F=43°19',则∠A的度数为 ( )
A. 42° B. 41°20' C. 41° D. 40°20'
7. 如图,边长为2的正六边形ABCDEF内接于☉O,则它的内切圆半径为 ( )
A. 1 B. 2 C. D.
8. 如图,有一块长为4cm、宽为3cm的矩形木板在桌面上按顺时针方向无滑动地翻滚,木板的顶点A的位置变化为A→A1→A2.其中,第二次翻滚时被桌面上一个小木块挡住,使木板边沿A2C与桌面成30°角,则点A翻滚到点A2的位置经过的路径长为 ( )
A. 10cm B. 3.5πcm
C. 4.5πcm D. 2.5πcm
二、 填空题(每小题3分,共24分)
9. 学校广播站要新招1名广播员,甲、乙两名同学经过选拔进入到复试环节,参加了口语表达、写作能力两项测试,成绩(单位:分)如表所示.学校规定口语表达按70%,写作能力按30%计入总成绩,根据总成绩择优录取.通过计算,你认为 同学将被录取(填“甲”或“乙”).
项目应试者 口语表达 写作能力
甲 80 90
乙 90 80
10. 一组数据2、3、3、4,则这组数据的方差为 .
11. 关于x的一元二次方程x2+6x+m=0有两个相等的实数根,则m的值为 .
12. 如图所示为从正面看到的一个碗的形状示意图,是☉O的一部分,D是的中点,连接OD,与弦AB交于点C,连接OA、OB.已知AB=24cm,CD=8cm,则☉O的半径OA为 cm.
13. 随着经济复苏,某公司近两年的总收入逐年递增.该公司2021年缴税40万元,2023年缴税48.4万元.该公司这两年缴税的年平均增长率是 .
14. 已知实数x1、x2(x1≠x2)是关于x的方程kx2+2kx+1=0(k≠0)的两个根.若+=2,则k的值为 .
15. 如图,☉O是小正方形的外接圆,是大正方形的内切圆.现假设可以随意在图中取点,则这个点取在涂色部分的概率是 .
16. 如图,∠ACB=45°,半径为2的☉O与∠ACB的两边相切,P是☉O上任意一点,过点P向∠ACB的两边作垂线,垂足分别为E、F,设t=PE+PF,则t的取值范围是
.
三、 解答题(共82分)
17. (5分)解方程:2x2-5x-1=0.
18. (5分)规定:对于任意实数a、b、c,有【a,b】★c=ac+b,其中等式右侧是通常的乘法和加法运算,如【2,3】★1=2×1+3=5.若关于x的方程【x,x+1】★(mx)=0有两个不相等的实数根,试确定m的取值范围.
19. (6分)若矩形相邻两边长a、b是关于x的方程x2-kx+k+4=0的两根,且a、b满足a2+b2=40,求k的值.
20. (6分)在3张相同的小纸条上分别写有“石头”“剪子”“布”.将这3张小纸条做成3支签,放在不透明的盒子中搅匀.
(1) 从盒子中任意抽出1支签,抽到“石头”的概率是 .
(2) 甲、乙两人通过抽签分胜负,规定:“石头”胜“剪子”,“剪子”胜“布”,“布”胜“石头”.甲先从盒子中任意抽出1支签(不放回),乙再从余下的2支签中任意抽出1支签,求甲取胜的概率.
21. (6分)如图,四边形ABCD是☉O的内接四边形,AB是☉O的直径,∠ABD=45°,直线l与三条线段CD、CA、DA的延长线分别交于点E、F、G,且满足∠CFE=45°.
(1) 求证:l⊥CE;
(2) 若AB=DG,求证:△ABC≌△GDE.
第21题
22. (8分)在某购物电商平台上,客户购买商家的商品后,可从“产品质量”“商家服务”“发货速度”“快递服务”等方面给予商家分值评价(分值为1分、2分、3分、4分和5分).该平台上甲、乙两个商家以相同价格分别销售同款T恤衫,平台为了了解他们的客户对其“商家服务”的评价情况,从甲、乙两个商家各随机抽取了一部分“商家服务”的评价分值进行统计分析.
【数据描述】
如图①②是根据样本数据制作的不完整的统计图,请回答问题(1)(2).
(1) 平台从甲、乙两个商家分别抽取了多少个评价分值 请补全条形统计图.
(2) 求甲商家的“商家服务”评价分值的扇形统计图中圆心角α的度数.
【分析与应用】
样本数据的统计量如下表,请回答问题(3)(4).
商 家 统计量
中位数 众 数 平均数 方 差
甲 a 3 3.5 1.05
乙 4 b 1.24
(3) 直接写出表中a和b的值,并求的值.
(4) 小亮打算从甲、乙两个商家中选择“商家服务”好的一个购买此款T恤衫.你认为小亮应该选择哪一个
23. (8分)某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克.后来经过市场调查发现:每千克的售价每降低2元,则平均每天的销售量可增加20千克.已知该专卖店销售这种核桃想要平均每天获利2240元.
(1) 每千克核桃应降价多少元
(2) 在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,则该专卖店应按原售价的几折出售核桃
24. (8分)如图,一个可以自由转动的转盘被分成4个相同的扇形,这些扇形内分别标有数字2、5、5、3,指针的位置固定.转动转盘,当转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,计为转动转盘一次(若指针指向两个扇形的分割线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止).
(1) 转动转盘一次,转出的数字为2的概率是 ;
(2) 转动转盘两次,请利用画树状图或列表的方法,求这两次转出的数字之和是5的倍数的概率.
第24题
25. (10分)如图,BE是☉O的直径,点A在☉O上,点C在BE的延长线上,∠EAC=∠ABC,AD平分∠BAE交☉O于点D,连接DE.
(1) 求证:CA是☉O的切线;
(2) 当AC=8,CE=4时,求DE的长.
第25题
26. (10分)如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B按逆时针方向旋转90°后,点E落在CB延长线上的点F处,点C落在点A处;再将线段AF绕点F按顺时针方向旋转90°得到线段GF,连接EF、CG.
(1) 求证:EF∥CG;
(2) 求点C、A在旋转过程中形成的、与线段CG所围成的阴影部分的面积.
第26题
27. (10分)等腰直角三角形ABC和☉O按如图所示的方式放置在水平线l上,AB=BC=1cm,∠ABC=90°,☉O的半径为1cm,圆心O与直线AB的距离为5cm.现△ABC以2cm/s的速度向右移动,同时△ABC的边AB、BC又以0.5cm/s的速度沿BA、BC方向增大.
(1) 当△ABC的边(边BC除外)与圆第一次相切时,求点B移动的距离;
(2) 若在△ABC移动的同时,☉O也以1cm/s的速度向右移动,则△ABC从开始移动到它的边(边BC除外)与圆最后一次相切,一共经过了 s.
第27题
期末素能测评
一、 1. C 2. D 3. B 4. D 5. A 6. C 7. D 8. B
二、 9. 乙 10. 0.5 11. 9 12. 13 13. 10%
14. -1 15.
16. 2≤t≤4+2 解析:延长EP交直线CB于点Q,则易得PQ=PF.此时t=PE+PF=PE+PQ=EQ.当EQ与☉O相切且点P在圆心的右侧时,t有最大值4+2;当EQ与☉O相切且点P在圆心的左侧时,t有最小值2,∴ t的取值范围是2≤t≤4+2.
三、 17. x1=,x2=
18. 根据题意,【x,x+1】★(mx)=0可化为x(mx)+x+1=0,整理,得mx2+x+1=0.∵ 上述方程有两个不相等的实数根,∴ 根的判别式12-4m·1>0且m≠0,解得m<且m≠0,∴ m的取值范围是m<且m≠0
19. ∵ a、b为方程x2-kx+k+4=0的两根,∴ a+b=k,ab=k+4.∵ a2+b2=40,∴ (a+b)2-2ab=40,即k2-2(k+4)=40,整理,得k2-2k-48=0,解得k1=8,k2=-6(不合题意,舍去),∴ k的值为8
20. (1) (2) 画树状图如图所示.由树状图,可知甲、乙两人分别抽签共有6种等可能的结果,其中甲取胜的结果有(石头,剪子)、(剪子,布)、(布,石头)共3种,∴ P(甲取胜)==
21. (1) ∵ 在☉O中,=,∠ABD=45°,∴ ∠ACD=∠ABD=45°,即∠FCE=45°.∵ △FCE的内角和为180°,∠CFE=45°,∴ ∠CEF=180°-∠CFE-∠FCE=180°-45°-45°=90°,∴ l⊥CE (2) ∵ 四边形ABCD是☉O的内接四边形,∴ ∠ABC+∠ADC=180°.∵ ∠GDE+∠ADC=180°,∴ ∠ABC=∠GDE.∵ AB为☉O的直径,∴ ∠ACB=90°.由(1),知∠CEF=90°,即∠GED=90°,∴ ∠ACB=∠GED.在△ABC和△GDE中,∴ △ABC≌△GDE
22. (1) 由题意可得,平台从甲商家抽取了12÷40%=30(个)评价分值,从乙商家抽取了3÷15%=20(个)评价分值,∴ 甲商家4分的评价分值个数为30-2-1-12-5=10,乙商家4分的评价分值个数为20-1-3-3-4=9,由此补全条形统计图如图所示 (2) α=360°×=120° (3) a=3.5,b=4.乙商家数据的平均数=×(1×1+2×3+3×3+4×9+5×4)=3.6 (4) 由统计表可知,乙商家的中位数、众数和平均数都高于甲商家的,方差较接近,∴ 小亮应该选择乙商家
23. (1) 设每千克核桃应降价x元.根据题意,得(60-x-40)100+·20=2240,解得x1=4,x2=6.答:每千克核桃应降价4元或6元 (2) 由(1),可知每千克核桃可降价4元或6元.∵ 要尽可能让利于顾客,∴ 每千克核桃应降价6元.此时每千克的售价为60-6=54(元),×100%=90%.答:该专卖店应按原售价的9折出售核桃
24. (1) (2) 列表如下:
第2次和第1次 2 5 5 3
2 4 7 7 5
5 7 10 10 8
5 7 10 10 8
3 5 8 8 6
由表格,可知转动转盘两次共有16种等可能的结果,其中这两次转出的数字之和是5的倍数的结果有6种,∴ P(这两次转出的数字之和是5的倍数)==
25. (1) 如图,连接OA.∵ BE是☉O的直径,∴ ∠BAE=90°,∴ ∠BAO+∠OAE=90°.∵ OA=OB,∴ ∠ABC=∠BAO.∵ ∠EAC=∠ABC,∴ ∠EAC=∠BAO,∴ ∠EAC+∠OAE=90°,即∠OAC=90°,∴ OA⊥AC.∵ OA是☉O的半径,∴ CA是☉O的切线
(2) 如图,连接BD.设☉O的半径为r,则OA=OE=r.∵ ∠OAC=90°,∴ OA2+AC2=OC2.∵ AC=8,CE=4,∴ r2+82=(4+r)2,解得r=6,∴ BE=2r=12.∵ AD平分∠BAE,∴ ∠BAD=∠EAD,∴ =,∴ BD=DE.∵ BE是☉O的直径,∴ ∠BDE=90°,∴ BD2+DE2=BE2,即DE2+DE2=122,∴ DE=6
26. (1) ∵ 四边形ABCD是正方形,∴ AB=BC=AD=2,∠ABC=90°.∵ △BEC绕点B按逆时针方向旋转90°得到△BFA,∴ △BFA≌△BEC,∴ ∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=CE,∴ ∠AFB+∠FAB=90°.∵ 线段AF绕点F按顺时针方向旋转90°得到线段GF,∴ ∠AFB+∠CFG=∠AFG=90°,AF=GF,∴ ∠CFG=∠FAB=∠ECB,∴ EC∥GF.∵ AF=CE,AF=GF,∴ CE=GF,∴ 四边形EFGC是平行四边形,∴ EF∥CG (2) ∵ E是AB的中点,∴ EB=AB=1.∵ △BFA≌△BEC,∴ FB=EB=1,∴ AF==.∵ CF是 EFGC的对角线,∴ S△FEC=S△CGF,∴ S阴影=S扇形BAC+S△ABF+S△CGF-S扇形FAG=S扇形BAC+S△ABF+S△FEC-S扇形FAG=+×2×1+×(1+2)×1-=-
27. (1) 设第一次相切时,△ABC移动至△A'B'C'处,如图,设A'C'与☉O相切于点E,连接OE并延长,交B'C'于点F.设☉O与直线l相切于点D,连接OD,则OE⊥A'C',OD⊥l.由切线长定理,可知C'E=C'D,设C'D=xcm,则C'E=xcm.在Rt△C'EF中,由题意易得∠A'C'B'=∠EFC'=45°,∴ 易知C'F=xcm,且在Rt△OFD中,FD=OD=1cm,∴ x+x=1,∴ x=-1,∴ CC'=5-1-(-1)=(5-)cm,∴ 点C移动的时间为(5-)÷(2+0.5)=(s),∴ 点B移动的距离为×2=(cm)
(2) 6 解析:∵ △ABC与☉O最后一次相切,是边AB与☉O相切,且圆心在AB的左侧,∴ 路程差为6cm,速度差为1cm/s,∴ △ABC从开始移动到它的边(边BC除外)与圆最后一次相切,一共经过了6÷1=6(s).
一、 选择题(每小题3分,共24分)
1.
有一组数据:31、32、35、37、35.这组数据的平均数和中位数分别是 ( )
A. 34、34 B. 35、35
C. 34、35 D. 35、34
2. 不透明袋子中装有白球2个,红球1个,这些球除了颜色外无其他差别.从袋子中随机取出1个球,取出白球的概率是 ( )
A. 1 B. C. D.
3. 关于x的一元二次方程2x2-3x+k=0有实数根,则实数k的取值范围是 ( )
A. k< B. k≤ C. k≥ D. k<-
4. 某年级举办篮球友谊赛,参赛的每两个球队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队个数是 ( )
A. 6 B. 7 C. 8 D. 9
5. 若圆锥侧面展开图的面积是15π,母线长是5,则这个圆锥的底面圆的半径是 ( )
A. 3 B. 4 C. 5 D. 6
6. 如图,分别延长圆内接四边形ABCD的两组对边,延长线相交于点E、F.若∠E=54°41',∠F=43°19',则∠A的度数为 ( )
A. 42° B. 41°20' C. 41° D. 40°20'
7. 如图,边长为2的正六边形ABCDEF内接于☉O,则它的内切圆半径为 ( )
A. 1 B. 2 C. D.
8. 如图,有一块长为4cm、宽为3cm的矩形木板在桌面上按顺时针方向无滑动地翻滚,木板的顶点A的位置变化为A→A1→A2.其中,第二次翻滚时被桌面上一个小木块挡住,使木板边沿A2C与桌面成30°角,则点A翻滚到点A2的位置经过的路径长为 ( )
A. 10cm B. 3.5πcm
C. 4.5πcm D. 2.5πcm
二、 填空题(每小题3分,共24分)
9. 学校广播站要新招1名广播员,甲、乙两名同学经过选拔进入到复试环节,参加了口语表达、写作能力两项测试,成绩(单位:分)如表所示.学校规定口语表达按70%,写作能力按30%计入总成绩,根据总成绩择优录取.通过计算,你认为 同学将被录取(填“甲”或“乙”).
项目应试者 口语表达 写作能力
甲 80 90
乙 90 80
10. 一组数据2、3、3、4,则这组数据的方差为 .
11. 关于x的一元二次方程x2+6x+m=0有两个相等的实数根,则m的值为 .
12. 如图所示为从正面看到的一个碗的形状示意图,是☉O的一部分,D是的中点,连接OD,与弦AB交于点C,连接OA、OB.已知AB=24cm,CD=8cm,则☉O的半径OA为 cm.
13. 随着经济复苏,某公司近两年的总收入逐年递增.该公司2021年缴税40万元,2023年缴税48.4万元.该公司这两年缴税的年平均增长率是 .
14. 已知实数x1、x2(x1≠x2)是关于x的方程kx2+2kx+1=0(k≠0)的两个根.若+=2,则k的值为 .
15. 如图,☉O是小正方形的外接圆,是大正方形的内切圆.现假设可以随意在图中取点,则这个点取在涂色部分的概率是 .
16. 如图,∠ACB=45°,半径为2的☉O与∠ACB的两边相切,P是☉O上任意一点,过点P向∠ACB的两边作垂线,垂足分别为E、F,设t=PE+PF,则t的取值范围是
.
三、 解答题(共82分)
17. (5分)解方程:2x2-5x-1=0.
18. (5分)规定:对于任意实数a、b、c,有【a,b】★c=ac+b,其中等式右侧是通常的乘法和加法运算,如【2,3】★1=2×1+3=5.若关于x的方程【x,x+1】★(mx)=0有两个不相等的实数根,试确定m的取值范围.
19. (6分)若矩形相邻两边长a、b是关于x的方程x2-kx+k+4=0的两根,且a、b满足a2+b2=40,求k的值.
20. (6分)在3张相同的小纸条上分别写有“石头”“剪子”“布”.将这3张小纸条做成3支签,放在不透明的盒子中搅匀.
(1) 从盒子中任意抽出1支签,抽到“石头”的概率是 .
(2) 甲、乙两人通过抽签分胜负,规定:“石头”胜“剪子”,“剪子”胜“布”,“布”胜“石头”.甲先从盒子中任意抽出1支签(不放回),乙再从余下的2支签中任意抽出1支签,求甲取胜的概率.
21. (6分)如图,四边形ABCD是☉O的内接四边形,AB是☉O的直径,∠ABD=45°,直线l与三条线段CD、CA、DA的延长线分别交于点E、F、G,且满足∠CFE=45°.
(1) 求证:l⊥CE;
(2) 若AB=DG,求证:△ABC≌△GDE.
第21题
22. (8分)在某购物电商平台上,客户购买商家的商品后,可从“产品质量”“商家服务”“发货速度”“快递服务”等方面给予商家分值评价(分值为1分、2分、3分、4分和5分).该平台上甲、乙两个商家以相同价格分别销售同款T恤衫,平台为了了解他们的客户对其“商家服务”的评价情况,从甲、乙两个商家各随机抽取了一部分“商家服务”的评价分值进行统计分析.
【数据描述】
如图①②是根据样本数据制作的不完整的统计图,请回答问题(1)(2).
(1) 平台从甲、乙两个商家分别抽取了多少个评价分值 请补全条形统计图.
(2) 求甲商家的“商家服务”评价分值的扇形统计图中圆心角α的度数.
【分析与应用】
样本数据的统计量如下表,请回答问题(3)(4).
商 家 统计量
中位数 众 数 平均数 方 差
甲 a 3 3.5 1.05
乙 4 b 1.24
(3) 直接写出表中a和b的值,并求的值.
(4) 小亮打算从甲、乙两个商家中选择“商家服务”好的一个购买此款T恤衫.你认为小亮应该选择哪一个
23. (8分)某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克.后来经过市场调查发现:每千克的售价每降低2元,则平均每天的销售量可增加20千克.已知该专卖店销售这种核桃想要平均每天获利2240元.
(1) 每千克核桃应降价多少元
(2) 在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,则该专卖店应按原售价的几折出售核桃
24. (8分)如图,一个可以自由转动的转盘被分成4个相同的扇形,这些扇形内分别标有数字2、5、5、3,指针的位置固定.转动转盘,当转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,计为转动转盘一次(若指针指向两个扇形的分割线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止).
(1) 转动转盘一次,转出的数字为2的概率是 ;
(2) 转动转盘两次,请利用画树状图或列表的方法,求这两次转出的数字之和是5的倍数的概率.
第24题
25. (10分)如图,BE是☉O的直径,点A在☉O上,点C在BE的延长线上,∠EAC=∠ABC,AD平分∠BAE交☉O于点D,连接DE.
(1) 求证:CA是☉O的切线;
(2) 当AC=8,CE=4时,求DE的长.
第25题
26. (10分)如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B按逆时针方向旋转90°后,点E落在CB延长线上的点F处,点C落在点A处;再将线段AF绕点F按顺时针方向旋转90°得到线段GF,连接EF、CG.
(1) 求证:EF∥CG;
(2) 求点C、A在旋转过程中形成的、与线段CG所围成的阴影部分的面积.
第26题
27. (10分)等腰直角三角形ABC和☉O按如图所示的方式放置在水平线l上,AB=BC=1cm,∠ABC=90°,☉O的半径为1cm,圆心O与直线AB的距离为5cm.现△ABC以2cm/s的速度向右移动,同时△ABC的边AB、BC又以0.5cm/s的速度沿BA、BC方向增大.
(1) 当△ABC的边(边BC除外)与圆第一次相切时,求点B移动的距离;
(2) 若在△ABC移动的同时,☉O也以1cm/s的速度向右移动,则△ABC从开始移动到它的边(边BC除外)与圆最后一次相切,一共经过了 s.
第27题
期末素能测评
一、 1. C 2. D 3. B 4. D 5. A 6. C 7. D 8. B
二、 9. 乙 10. 0.5 11. 9 12. 13 13. 10%
14. -1 15.
16. 2≤t≤4+2 解析:延长EP交直线CB于点Q,则易得PQ=PF.此时t=PE+PF=PE+PQ=EQ.当EQ与☉O相切且点P在圆心的右侧时,t有最大值4+2;当EQ与☉O相切且点P在圆心的左侧时,t有最小值2,∴ t的取值范围是2≤t≤4+2.
三、 17. x1=,x2=
18. 根据题意,【x,x+1】★(mx)=0可化为x(mx)+x+1=0,整理,得mx2+x+1=0.∵ 上述方程有两个不相等的实数根,∴ 根的判别式12-4m·1>0且m≠0,解得m<且m≠0,∴ m的取值范围是m<且m≠0
19. ∵ a、b为方程x2-kx+k+4=0的两根,∴ a+b=k,ab=k+4.∵ a2+b2=40,∴ (a+b)2-2ab=40,即k2-2(k+4)=40,整理,得k2-2k-48=0,解得k1=8,k2=-6(不合题意,舍去),∴ k的值为8
20. (1) (2) 画树状图如图所示.由树状图,可知甲、乙两人分别抽签共有6种等可能的结果,其中甲取胜的结果有(石头,剪子)、(剪子,布)、(布,石头)共3种,∴ P(甲取胜)==
21. (1) ∵ 在☉O中,=,∠ABD=45°,∴ ∠ACD=∠ABD=45°,即∠FCE=45°.∵ △FCE的内角和为180°,∠CFE=45°,∴ ∠CEF=180°-∠CFE-∠FCE=180°-45°-45°=90°,∴ l⊥CE (2) ∵ 四边形ABCD是☉O的内接四边形,∴ ∠ABC+∠ADC=180°.∵ ∠GDE+∠ADC=180°,∴ ∠ABC=∠GDE.∵ AB为☉O的直径,∴ ∠ACB=90°.由(1),知∠CEF=90°,即∠GED=90°,∴ ∠ACB=∠GED.在△ABC和△GDE中,∴ △ABC≌△GDE
22. (1) 由题意可得,平台从甲商家抽取了12÷40%=30(个)评价分值,从乙商家抽取了3÷15%=20(个)评价分值,∴ 甲商家4分的评价分值个数为30-2-1-12-5=10,乙商家4分的评价分值个数为20-1-3-3-4=9,由此补全条形统计图如图所示 (2) α=360°×=120° (3) a=3.5,b=4.乙商家数据的平均数=×(1×1+2×3+3×3+4×9+5×4)=3.6 (4) 由统计表可知,乙商家的中位数、众数和平均数都高于甲商家的,方差较接近,∴ 小亮应该选择乙商家
23. (1) 设每千克核桃应降价x元.根据题意,得(60-x-40)100+·20=2240,解得x1=4,x2=6.答:每千克核桃应降价4元或6元 (2) 由(1),可知每千克核桃可降价4元或6元.∵ 要尽可能让利于顾客,∴ 每千克核桃应降价6元.此时每千克的售价为60-6=54(元),×100%=90%.答:该专卖店应按原售价的9折出售核桃
24. (1) (2) 列表如下:
第2次和第1次 2 5 5 3
2 4 7 7 5
5 7 10 10 8
5 7 10 10 8
3 5 8 8 6
由表格,可知转动转盘两次共有16种等可能的结果,其中这两次转出的数字之和是5的倍数的结果有6种,∴ P(这两次转出的数字之和是5的倍数)==
25. (1) 如图,连接OA.∵ BE是☉O的直径,∴ ∠BAE=90°,∴ ∠BAO+∠OAE=90°.∵ OA=OB,∴ ∠ABC=∠BAO.∵ ∠EAC=∠ABC,∴ ∠EAC=∠BAO,∴ ∠EAC+∠OAE=90°,即∠OAC=90°,∴ OA⊥AC.∵ OA是☉O的半径,∴ CA是☉O的切线
(2) 如图,连接BD.设☉O的半径为r,则OA=OE=r.∵ ∠OAC=90°,∴ OA2+AC2=OC2.∵ AC=8,CE=4,∴ r2+82=(4+r)2,解得r=6,∴ BE=2r=12.∵ AD平分∠BAE,∴ ∠BAD=∠EAD,∴ =,∴ BD=DE.∵ BE是☉O的直径,∴ ∠BDE=90°,∴ BD2+DE2=BE2,即DE2+DE2=122,∴ DE=6
26. (1) ∵ 四边形ABCD是正方形,∴ AB=BC=AD=2,∠ABC=90°.∵ △BEC绕点B按逆时针方向旋转90°得到△BFA,∴ △BFA≌△BEC,∴ ∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=CE,∴ ∠AFB+∠FAB=90°.∵ 线段AF绕点F按顺时针方向旋转90°得到线段GF,∴ ∠AFB+∠CFG=∠AFG=90°,AF=GF,∴ ∠CFG=∠FAB=∠ECB,∴ EC∥GF.∵ AF=CE,AF=GF,∴ CE=GF,∴ 四边形EFGC是平行四边形,∴ EF∥CG (2) ∵ E是AB的中点,∴ EB=AB=1.∵ △BFA≌△BEC,∴ FB=EB=1,∴ AF==.∵ CF是 EFGC的对角线,∴ S△FEC=S△CGF,∴ S阴影=S扇形BAC+S△ABF+S△CGF-S扇形FAG=S扇形BAC+S△ABF+S△FEC-S扇形FAG=+×2×1+×(1+2)×1-=-
27. (1) 设第一次相切时,△ABC移动至△A'B'C'处,如图,设A'C'与☉O相切于点E,连接OE并延长,交B'C'于点F.设☉O与直线l相切于点D,连接OD,则OE⊥A'C',OD⊥l.由切线长定理,可知C'E=C'D,设C'D=xcm,则C'E=xcm.在Rt△C'EF中,由题意易得∠A'C'B'=∠EFC'=45°,∴ 易知C'F=xcm,且在Rt△OFD中,FD=OD=1cm,∴ x+x=1,∴ x=-1,∴ CC'=5-1-(-1)=(5-)cm,∴ 点C移动的时间为(5-)÷(2+0.5)=(s),∴ 点B移动的距离为×2=(cm)
(2) 6 解析:∵ △ABC与☉O最后一次相切,是边AB与☉O相切,且圆心在AB的左侧,∴ 路程差为6cm,速度差为1cm/s,∴ △ABC从开始移动到它的边(边BC除外)与圆最后一次相切,一共经过了6÷1=6(s).
同课章节目录
