期中素能测评 (含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 期中素能测评 (含答案) 2025-2026学年数学苏科版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 205.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 16:39:32 | ||
图片预览


文档简介
期中素能测评
一、 选择题(每小题3分,共24分)
1.
利用公式法解得方程3x2-11x-1=0 的两解分别为a、b,且a>b,则a的值为 ( )
A. B.
C. D.
2. 下列圆的内接正多边形中,一条边所对的圆心角最大的图形是 ( )
A. 正三角形 B. 正方形
C. 正五边形 D. 正六边形
3. 已知关于x的方程x2-(2k-2)x+k2-1=0有两个实数根,则实数k的取值范围是 ( )
A. k<1 B. k≤1
C. k>1 D. k≥1
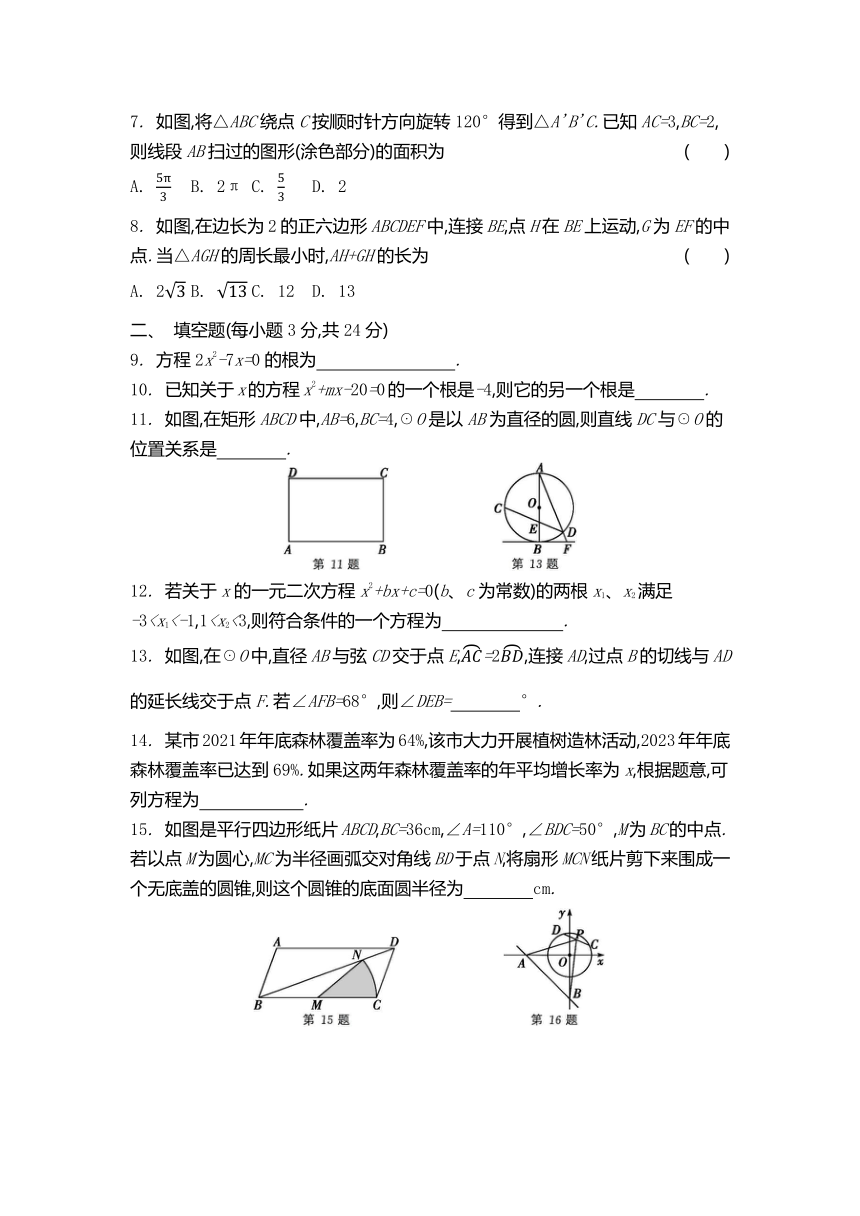
4. 如图,AB是☉O的直径,∠E=35°,则∠BOD的度数为 ( )
A. 80° B. 100° C. 120° D. 110°
5. 已知a和b是方程x2+2024x-4=0的两个实数根,则a2+2023a-b的值为 ( )
A. 2025 B. 2026 C. 2027 D. 2028
6. 如图,AB是☉O的切线,A为切点,连接OA,点C在☉O上,OC⊥OA,连接BC并延长,交☉O于点D,连接OD.若∠B=65°,则∠DOC的度数为 ( )
A. 45° B. 50° C. 65° D. 75°
7. 如图,将△ABC绕点C按顺时针方向旋转120°得到△A'B'C.已知AC=3,BC=2,则线段AB扫过的图形(涂色部分)的面积为 ( )
A. B. 2π C. D. 2
8. 如图,在边长为2的正六边形ABCDEF中,连接BE,点H在BE上运动,G为EF的中点.当△AGH的周长最小时,AH+GH的长为 ( )
A. 2 B. C. 12 D. 13
二、 填空题(每小题3分,共24分)
9. 方程2x2-7x=0的根为 .
10. 已知关于x的方程x2+mx-20=0的一个根是-4,则它的另一个根是 .
11. 如图,在矩形ABCD中,AB=6,BC=4,☉O是以AB为直径的圆,则直线DC与☉O的位置关系是 .
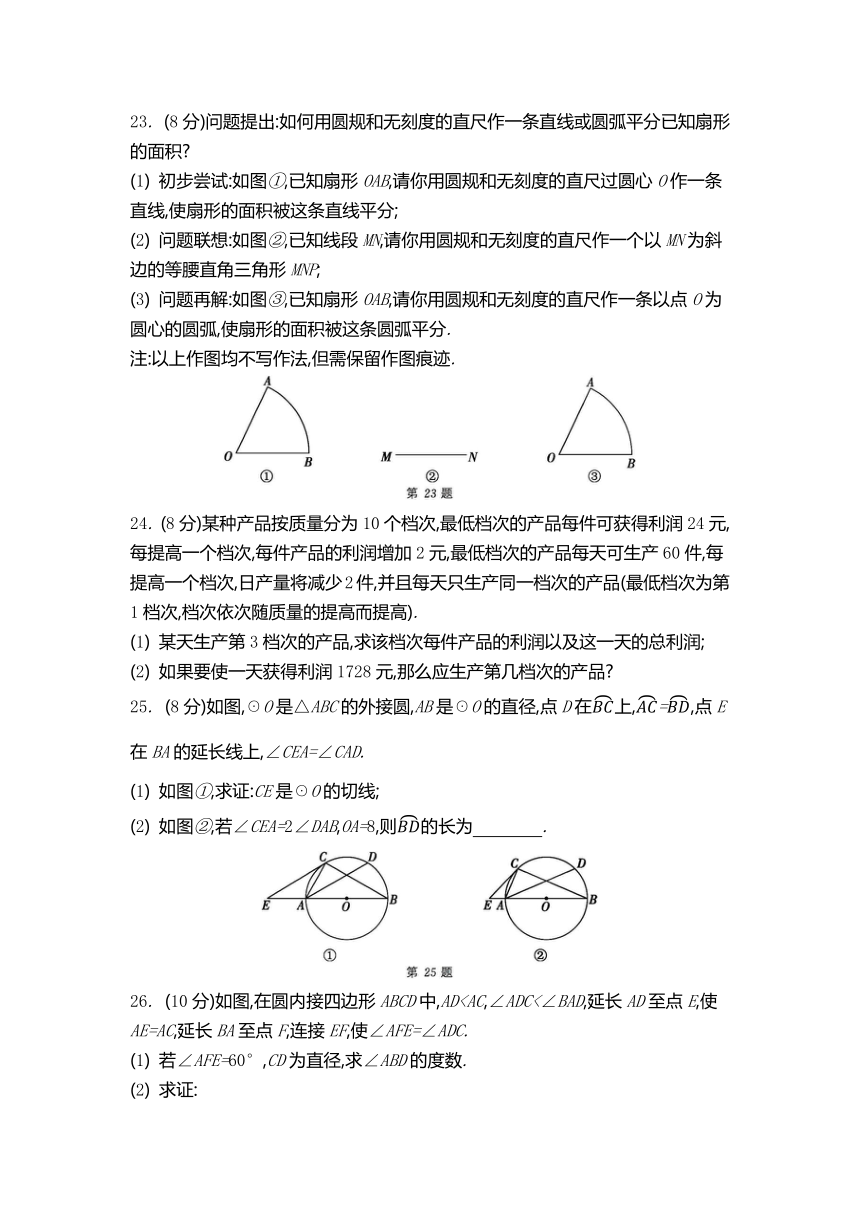
12. 若关于x的一元二次方程x2+bx+c=0(b、c为常数)的两根x1、x2满足-313. 如图,在☉O中,直径AB与弦CD交于点E,=2,连接AD,过点B的切线与AD的延长线交于点F.若∠AFB=68°,则∠DEB= °.
14. 某市2021年年底森林覆盖率为64%,该市大力开展植树造林活动,2023年年底森林覆盖率已达到69%.如果这两年森林覆盖率的年平均增长率为x,根据题意,可列方程为 .
15. 如图是平行四边形纸片ABCD,BC=36cm,∠A=110°,∠BDC=50°,M为BC的中点.若以点M为圆心,MC为半径画弧交对角线BD于点N,将扇形MCN纸片剪下来围成一个无底盖的圆锥,则这个圆锥的底面圆半径为 cm.
16. 如图,在平面直角坐标系中,直线y=-x-2与x轴、y轴分别交于A、B两点,C、D是半径为1的☉O上的两动点,且CD=,P为弦CD的中点.当C、D两点在圆上运动时,△PAB面积的最大值为 .
三、 解答题(共82分)
17. (6分)解下列方程:
(1) x(x-5)=15-3x; (2) 2x2=3(x+2).
18. (6分)已知关于x的一元二次方程2x2+(3m-2)x-6=0的两根互为相反数,求m的值.
19. (6分)已知T=(a+3b)2+(2a+3b)(2a-3b)+a2.
(1) 化简T;
(2) 若关于x的方程x2+2ax-ab+1=0有两个相等的实数根,求T的值.
20. (6分)如图,在打印图片之前,为确定打印区域,需设置纸张大小和页边距(纸张的边线到打印区域的距离),上、下、左、右的页边距分别为acm、bcm、ccm、dcm.若纸张大小为16cm×10cm,考虑到整体的美观性,要求各页边距相等并使打印区域的面积占纸张的70%,则需如何设置页边距
第20题
21. (6分)如图,在☉O中,C是弦AB上的一个动点,连接OC,过点C作CD⊥OC,交☉O于点D.
(1) 当点C在AB的什么位置时,CD的长取得最大值
(2) 若AB=1,求CD长的最大值.
第21题
22. (8分)已知关于x的一元二次方程x2-(2m+1)x+m2+m=0.
(1) 求证:无论m取何值,方程都有两个不相等的实数根.
(2) 设该方程的两个实数根分别为a、b.若(2a+b)(a+2b)=20,求m的值.
23. (8分)问题提出:如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积
(1) 初步尝试:如图①,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
(2) 问题联想:如图②,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;
(3) 问题再解:如图③,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.
注:以上作图均不写作法,但需保留作图痕迹.
24. (8分)某种产品按质量分为10个档次,最低档次的产品每件可获得利润24元,每提高一个档次,每件产品的利润增加2元,最低档次的产品每天可生产60件,每提高一个档次,日产量将减少2件,并且每天只生产同一档次的产品(最低档次为第1档次,档次依次随质量的提高而提高).
(1) 某天生产第3档次的产品,求该档次每件产品的利润以及这一天的总利润;
(2) 如果要使一天获得利润1728元,那么应生产第几档次的产品
25. (8分)如图,☉O是△ABC的外接圆,AB是☉O的直径,点D在上,=,点E在BA的延长线上,∠CEA=∠CAD.
(1) 如图①,求证:CE是☉O的切线;
(2) 如图②,若∠CEA=2∠DAB,OA=8,则的长为 .
26. (10分)如图,在圆内接四边形ABCD中,AD(1) 若∠AFE=60°,CD为直径,求∠ABD的度数.
(2) 求证:
① EF∥BC;
② EF=BD.
第26题
27. (10分)如图①,在Rt△ABC中,∠ACB=90°,AC=BC,AB=10cm,点D从点A出发,沿射线AB以2cm/s的速度移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在射线AC、CB上).设点D移动的时间为ts.
(1) 若点D在边AB上,则当t为何值时,四边形DFCE的面积为12cm2
(2) 如图②,以点D为圆心,DE为半径作☉D.在点D沿射线AB移动的过程中,是否存在t的值,使☉D正好经过点B 若存在,请求出t的值;若不存在,请说明理由.
期中素能测评
一、 1. D 2. A 3. B 4. D 5. D 6. B 7. A 8. B
二、 9. x1=0,x2= 10. 5 11. 相离 12. 答案不唯一,如x2-2=0 13. 66 14. 64%(1+x)2=69% 15. 2
16. 3 解析:过点O作OQ⊥AB,连接OP、OD、OC.∵ CD=,OC=OD=1,∴ OC2+OD2=CD2,∴ △OCD为等腰直角三角形.∵ P为CD的中点,∴ OP=CD=.由直线y=-x-2与x轴、y轴分别交于A、B两点,得A(-2,0)、B(0,-2),∴ OA=OB=2,∴ △OAB为等腰直角三角形,∴ AB=2,OQ=.根据题意,易知当P、O、Q三点共线时,S△ABP最大,此时PQ=OP+OQ=,∴ △PAB面积的最大值为AB·PQ=3.
三、 17. (1) x1=5,x2=-3 (2) x1=,x2=
18. 设方程的两根为x1、x2,则x1+x2=-.∵ 方程2x2+(3m-2)x-6=0的两根互为相反数,∴ x1+x2=0,∴ -=0,解得m=
19. (1) T=(a+3b)2+(2a+3b)(2a-3b)+a2=a2+6ab+9b2+4a2-9b2+a2=6a2+6ab (2) ∵ 关于x的方程x2+2ax-ab+1=0有两个相等的实数根,∴ (2a)2-4(-ab+1)=0,∴ a2+ab=1,∴ T=6(a2+ab)=6×1=6
20. 设页边距为xcm.根据题意,得(16-2x)(10-2x)=16×10×70%,解得x1=1,x2=12(不合题意,舍去).答:设置页边距为1cm
21. (1) 连接OD.∵ CD⊥OC,∴ ∠DCO=90°,∴ CD=,∴ 当OC的长最小时,CD的长最大,∴ 当OC⊥AB时,OC的长最小,则CD的长取得最大值.根据垂径定理,可知点C在AB的中点位置 (2) 由(1),知OC⊥AB,∴ 此时D、B两点重合,∴ CD=CB=AB=×1=,即CD长的最大值为
22. (1) ∵ [-(2m+1)]2-4×1×(m2+m)=4m2+4m+1-4m2-4m=1>0,∴ 无论m取何值,方程都有两个不相等的实数根 (2) 根据一元二次方程的根与系数的关系,得a+b=2m+1,ab=m2+m.∵ (2a+b)(a+2b)=2a2+4ab+ab+2b2=2(a2+2ab+b2)+ab=2(a+b)2+ab,∴ 2(a+b)2+ab=20,即2(2m+1)2+m2+m=20.整理并化简,得m2+m-2=0,解得m1=-2,m2=1,∴ m的值为-2或1
23. (1) 如图①,直线OP即为所求作
(2) 如图②,△MNP即为所求作 解析:作线段MN的垂直平分线AB,交MN于点O.作直径为MN的圆交AB于点P,连接MP、NP.
(3) 如图③,即为所求作 解析:先作OB的垂直平分线,再作直径为OB的圆,与OB的垂直平分线交于点M,连接OM,以点O为圆心,OM为半径作弧,分别交OA、OB于点C、D.
24. (1) 该档次每件产品的利润为24+2×(3-1)=28(元),这一天的总利润为28×[60-2×(3-1)]=1568(元) (2) 设应生产第x档次的产品.根据题意,得[24+2×(x-1)]·[60-2×(x-1)]=1728.整理并化简,得x2-20x+91=0,解得x1=7,x2=13.∵ 产品按质量分为10个档次,∴ 1≤x≤10,且x为整数,∴ x=7.答:如果要使一天获得利润1728元,那么应生产第7档次的产品
25. (1) 如图①,连接OC.∵ ∠CAO是△ACE的一个外角,∴ ∠CAO=∠CEA+∠ACE,即∠CAD+∠DAB=∠CEA+∠ACE.∵ ∠CEA=∠CAD,∴ ∠DAB=∠ACE.∵ =,∴ ∠ABC=∠DAB,∴ ∠ABC=∠ACE.∵ AB是☉O的直径,∴ ∠ACB=90°,即∠ABC+∠OAC=90°.∵ OA=OC,∴ ∠OAC=∠OCA,∴ ∠ABC+∠OCA=90°,∴ ∠ACE+∠OCA=90°,即∠OCE=90°,∴ OC⊥CE.∵ OC是☉O的半径,∴ CE是☉O的切线
(2) 2π 解析:如图②,连接OD.设∠DAB=x.∵ ∠CEA=2∠DAB,∴ ∠CEA=2x.∵ ∠CEA=∠CAD,∴ ∠CAD=2x.∵ =,∴ ∠ABC=∠DAB=x.∵ AB是☉O的直径,∴ ∠ACB=90°,∴ ∠ABC+∠BAC=90°,即x+2x+x=90°,解得x=22.5°,∴ ∠DAB=22.5°.∵ =,∴ ∠BOD=2∠DAB=45°.∵ OA=OB=8,∴ 的长为=2π.
26. (1) ∵ CD为直径,∴ ∠CAD=90°.∵ ∠AFE=∠ADC,∠AFE=60°,∴ ∠ADC=60°.∵ △ADC的内角和为180°,∴ ∠ACD=180°-90°-60°=30°.∵ =,∴ ∠ABD=∠ACD=30° (2) ① ∵ 四边形ABCD是圆内接四边形,∴ ∠ABC+∠ADC=180°.∵ ∠AFE=∠ADC,∴ ∠ABC+∠AFE=180°,∴ EF∥BC ② 如图,过点D作DG∥BC交圆于点G,连接AG、CG.∵ DG∥BC,∴ ∠BCD=∠GDC,∴ =,∴ BD=CG.∵ 四边形ACGD是圆内接四边形,∴ ∠ACG+∠ADG=180°.∵ ∠EDG+∠ADG=180°,∴ ∠EDG=∠ACG.∵ EF∥BC,DG∥BC,∴ EF∥DG,∴ ∠AEF=∠EDG,∴ ∠AEF=∠ACG.∵ =,∴ ∠ADC=∠AGC.∵ ∠AFE=∠ADC,∴ ∠AFE=∠AGC.在△AEF和△ACG中,∴ △AEF≌△ACG,∴ EF=CG,∴ EF=BD
27. (1) ∵ 在Rt△ABC中,∠ACB=90°,AC=BC,AB=10cm,∴ 易得 AC=BC=5cm,∠A=45°.∵ DE∥BC,DF∥AC,∴ 四边形DFCE为平行四边形.∵ ∠ACB=90°,∴ 四边形DFCE为矩形,∴ ∠DEC=∠DEA=90°.∵ ∠A=45°,∴ △ADE是等腰直角三角形.由题意,得AD=2tcm,则易得AE=DE=tcm,EC=(5-t)cm.∴ t·(5-t)=12.整理,得t2-5t+6=0,解得t1=2,t2=3.∴ 当t的值为2或3时,四边形DFCE的面积为12cm2 (2) 存在 ∵ 点B在☉D上,∴ DB=DE.当点D在点B的左边时,由t=10-2t,解得t=10-5;当点D在点B的右边时,由t=2t-10,解得t=10+5.综上所述,当t的值为10-5或10+5时,☉D正好经过点B
一、 选择题(每小题3分,共24分)
1.
利用公式法解得方程3x2-11x-1=0 的两解分别为a、b,且a>b,则a的值为 ( )
A. B.
C. D.
2. 下列圆的内接正多边形中,一条边所对的圆心角最大的图形是 ( )
A. 正三角形 B. 正方形
C. 正五边形 D. 正六边形
3. 已知关于x的方程x2-(2k-2)x+k2-1=0有两个实数根,则实数k的取值范围是 ( )
A. k<1 B. k≤1
C. k>1 D. k≥1
4. 如图,AB是☉O的直径,∠E=35°,则∠BOD的度数为 ( )
A. 80° B. 100° C. 120° D. 110°
5. 已知a和b是方程x2+2024x-4=0的两个实数根,则a2+2023a-b的值为 ( )
A. 2025 B. 2026 C. 2027 D. 2028
6. 如图,AB是☉O的切线,A为切点,连接OA,点C在☉O上,OC⊥OA,连接BC并延长,交☉O于点D,连接OD.若∠B=65°,则∠DOC的度数为 ( )
A. 45° B. 50° C. 65° D. 75°
7. 如图,将△ABC绕点C按顺时针方向旋转120°得到△A'B'C.已知AC=3,BC=2,则线段AB扫过的图形(涂色部分)的面积为 ( )
A. B. 2π C. D. 2
8. 如图,在边长为2的正六边形ABCDEF中,连接BE,点H在BE上运动,G为EF的中点.当△AGH的周长最小时,AH+GH的长为 ( )
A. 2 B. C. 12 D. 13
二、 填空题(每小题3分,共24分)
9. 方程2x2-7x=0的根为 .
10. 已知关于x的方程x2+mx-20=0的一个根是-4,则它的另一个根是 .
11. 如图,在矩形ABCD中,AB=6,BC=4,☉O是以AB为直径的圆,则直线DC与☉O的位置关系是 .
12. 若关于x的一元二次方程x2+bx+c=0(b、c为常数)的两根x1、x2满足-3
14. 某市2021年年底森林覆盖率为64%,该市大力开展植树造林活动,2023年年底森林覆盖率已达到69%.如果这两年森林覆盖率的年平均增长率为x,根据题意,可列方程为 .
15. 如图是平行四边形纸片ABCD,BC=36cm,∠A=110°,∠BDC=50°,M为BC的中点.若以点M为圆心,MC为半径画弧交对角线BD于点N,将扇形MCN纸片剪下来围成一个无底盖的圆锥,则这个圆锥的底面圆半径为 cm.
16. 如图,在平面直角坐标系中,直线y=-x-2与x轴、y轴分别交于A、B两点,C、D是半径为1的☉O上的两动点,且CD=,P为弦CD的中点.当C、D两点在圆上运动时,△PAB面积的最大值为 .
三、 解答题(共82分)
17. (6分)解下列方程:
(1) x(x-5)=15-3x; (2) 2x2=3(x+2).
18. (6分)已知关于x的一元二次方程2x2+(3m-2)x-6=0的两根互为相反数,求m的值.
19. (6分)已知T=(a+3b)2+(2a+3b)(2a-3b)+a2.
(1) 化简T;
(2) 若关于x的方程x2+2ax-ab+1=0有两个相等的实数根,求T的值.
20. (6分)如图,在打印图片之前,为确定打印区域,需设置纸张大小和页边距(纸张的边线到打印区域的距离),上、下、左、右的页边距分别为acm、bcm、ccm、dcm.若纸张大小为16cm×10cm,考虑到整体的美观性,要求各页边距相等并使打印区域的面积占纸张的70%,则需如何设置页边距
第20题
21. (6分)如图,在☉O中,C是弦AB上的一个动点,连接OC,过点C作CD⊥OC,交☉O于点D.
(1) 当点C在AB的什么位置时,CD的长取得最大值
(2) 若AB=1,求CD长的最大值.
第21题
22. (8分)已知关于x的一元二次方程x2-(2m+1)x+m2+m=0.
(1) 求证:无论m取何值,方程都有两个不相等的实数根.
(2) 设该方程的两个实数根分别为a、b.若(2a+b)(a+2b)=20,求m的值.
23. (8分)问题提出:如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积
(1) 初步尝试:如图①,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
(2) 问题联想:如图②,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;
(3) 问题再解:如图③,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.
注:以上作图均不写作法,但需保留作图痕迹.
24. (8分)某种产品按质量分为10个档次,最低档次的产品每件可获得利润24元,每提高一个档次,每件产品的利润增加2元,最低档次的产品每天可生产60件,每提高一个档次,日产量将减少2件,并且每天只生产同一档次的产品(最低档次为第1档次,档次依次随质量的提高而提高).
(1) 某天生产第3档次的产品,求该档次每件产品的利润以及这一天的总利润;
(2) 如果要使一天获得利润1728元,那么应生产第几档次的产品
25. (8分)如图,☉O是△ABC的外接圆,AB是☉O的直径,点D在上,=,点E在BA的延长线上,∠CEA=∠CAD.
(1) 如图①,求证:CE是☉O的切线;
(2) 如图②,若∠CEA=2∠DAB,OA=8,则的长为 .
26. (10分)如图,在圆内接四边形ABCD中,AD
(2) 求证:
① EF∥BC;
② EF=BD.
第26题
27. (10分)如图①,在Rt△ABC中,∠ACB=90°,AC=BC,AB=10cm,点D从点A出发,沿射线AB以2cm/s的速度移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在射线AC、CB上).设点D移动的时间为ts.
(1) 若点D在边AB上,则当t为何值时,四边形DFCE的面积为12cm2
(2) 如图②,以点D为圆心,DE为半径作☉D.在点D沿射线AB移动的过程中,是否存在t的值,使☉D正好经过点B 若存在,请求出t的值;若不存在,请说明理由.
期中素能测评
一、 1. D 2. A 3. B 4. D 5. D 6. B 7. A 8. B
二、 9. x1=0,x2= 10. 5 11. 相离 12. 答案不唯一,如x2-2=0 13. 66 14. 64%(1+x)2=69% 15. 2
16. 3 解析:过点O作OQ⊥AB,连接OP、OD、OC.∵ CD=,OC=OD=1,∴ OC2+OD2=CD2,∴ △OCD为等腰直角三角形.∵ P为CD的中点,∴ OP=CD=.由直线y=-x-2与x轴、y轴分别交于A、B两点,得A(-2,0)、B(0,-2),∴ OA=OB=2,∴ △OAB为等腰直角三角形,∴ AB=2,OQ=.根据题意,易知当P、O、Q三点共线时,S△ABP最大,此时PQ=OP+OQ=,∴ △PAB面积的最大值为AB·PQ=3.
三、 17. (1) x1=5,x2=-3 (2) x1=,x2=
18. 设方程的两根为x1、x2,则x1+x2=-.∵ 方程2x2+(3m-2)x-6=0的两根互为相反数,∴ x1+x2=0,∴ -=0,解得m=
19. (1) T=(a+3b)2+(2a+3b)(2a-3b)+a2=a2+6ab+9b2+4a2-9b2+a2=6a2+6ab (2) ∵ 关于x的方程x2+2ax-ab+1=0有两个相等的实数根,∴ (2a)2-4(-ab+1)=0,∴ a2+ab=1,∴ T=6(a2+ab)=6×1=6
20. 设页边距为xcm.根据题意,得(16-2x)(10-2x)=16×10×70%,解得x1=1,x2=12(不合题意,舍去).答:设置页边距为1cm
21. (1) 连接OD.∵ CD⊥OC,∴ ∠DCO=90°,∴ CD=,∴ 当OC的长最小时,CD的长最大,∴ 当OC⊥AB时,OC的长最小,则CD的长取得最大值.根据垂径定理,可知点C在AB的中点位置 (2) 由(1),知OC⊥AB,∴ 此时D、B两点重合,∴ CD=CB=AB=×1=,即CD长的最大值为
22. (1) ∵ [-(2m+1)]2-4×1×(m2+m)=4m2+4m+1-4m2-4m=1>0,∴ 无论m取何值,方程都有两个不相等的实数根 (2) 根据一元二次方程的根与系数的关系,得a+b=2m+1,ab=m2+m.∵ (2a+b)(a+2b)=2a2+4ab+ab+2b2=2(a2+2ab+b2)+ab=2(a+b)2+ab,∴ 2(a+b)2+ab=20,即2(2m+1)2+m2+m=20.整理并化简,得m2+m-2=0,解得m1=-2,m2=1,∴ m的值为-2或1
23. (1) 如图①,直线OP即为所求作
(2) 如图②,△MNP即为所求作 解析:作线段MN的垂直平分线AB,交MN于点O.作直径为MN的圆交AB于点P,连接MP、NP.
(3) 如图③,即为所求作 解析:先作OB的垂直平分线,再作直径为OB的圆,与OB的垂直平分线交于点M,连接OM,以点O为圆心,OM为半径作弧,分别交OA、OB于点C、D.
24. (1) 该档次每件产品的利润为24+2×(3-1)=28(元),这一天的总利润为28×[60-2×(3-1)]=1568(元) (2) 设应生产第x档次的产品.根据题意,得[24+2×(x-1)]·[60-2×(x-1)]=1728.整理并化简,得x2-20x+91=0,解得x1=7,x2=13.∵ 产品按质量分为10个档次,∴ 1≤x≤10,且x为整数,∴ x=7.答:如果要使一天获得利润1728元,那么应生产第7档次的产品
25. (1) 如图①,连接OC.∵ ∠CAO是△ACE的一个外角,∴ ∠CAO=∠CEA+∠ACE,即∠CAD+∠DAB=∠CEA+∠ACE.∵ ∠CEA=∠CAD,∴ ∠DAB=∠ACE.∵ =,∴ ∠ABC=∠DAB,∴ ∠ABC=∠ACE.∵ AB是☉O的直径,∴ ∠ACB=90°,即∠ABC+∠OAC=90°.∵ OA=OC,∴ ∠OAC=∠OCA,∴ ∠ABC+∠OCA=90°,∴ ∠ACE+∠OCA=90°,即∠OCE=90°,∴ OC⊥CE.∵ OC是☉O的半径,∴ CE是☉O的切线
(2) 2π 解析:如图②,连接OD.设∠DAB=x.∵ ∠CEA=2∠DAB,∴ ∠CEA=2x.∵ ∠CEA=∠CAD,∴ ∠CAD=2x.∵ =,∴ ∠ABC=∠DAB=x.∵ AB是☉O的直径,∴ ∠ACB=90°,∴ ∠ABC+∠BAC=90°,即x+2x+x=90°,解得x=22.5°,∴ ∠DAB=22.5°.∵ =,∴ ∠BOD=2∠DAB=45°.∵ OA=OB=8,∴ 的长为=2π.
26. (1) ∵ CD为直径,∴ ∠CAD=90°.∵ ∠AFE=∠ADC,∠AFE=60°,∴ ∠ADC=60°.∵ △ADC的内角和为180°,∴ ∠ACD=180°-90°-60°=30°.∵ =,∴ ∠ABD=∠ACD=30° (2) ① ∵ 四边形ABCD是圆内接四边形,∴ ∠ABC+∠ADC=180°.∵ ∠AFE=∠ADC,∴ ∠ABC+∠AFE=180°,∴ EF∥BC ② 如图,过点D作DG∥BC交圆于点G,连接AG、CG.∵ DG∥BC,∴ ∠BCD=∠GDC,∴ =,∴ BD=CG.∵ 四边形ACGD是圆内接四边形,∴ ∠ACG+∠ADG=180°.∵ ∠EDG+∠ADG=180°,∴ ∠EDG=∠ACG.∵ EF∥BC,DG∥BC,∴ EF∥DG,∴ ∠AEF=∠EDG,∴ ∠AEF=∠ACG.∵ =,∴ ∠ADC=∠AGC.∵ ∠AFE=∠ADC,∴ ∠AFE=∠AGC.在△AEF和△ACG中,∴ △AEF≌△ACG,∴ EF=CG,∴ EF=BD
27. (1) ∵ 在Rt△ABC中,∠ACB=90°,AC=BC,AB=10cm,∴ 易得 AC=BC=5cm,∠A=45°.∵ DE∥BC,DF∥AC,∴ 四边形DFCE为平行四边形.∵ ∠ACB=90°,∴ 四边形DFCE为矩形,∴ ∠DEC=∠DEA=90°.∵ ∠A=45°,∴ △ADE是等腰直角三角形.由题意,得AD=2tcm,则易得AE=DE=tcm,EC=(5-t)cm.∴ t·(5-t)=12.整理,得t2-5t+6=0,解得t1=2,t2=3.∴ 当t的值为2或3时,四边形DFCE的面积为12cm2 (2) 存在 ∵ 点B在☉D上,∴ DB=DE.当点D在点B的左边时,由t=10-2t,解得t=10-5;当点D在点B的右边时,由t=2t-10,解得t=10+5.综上所述,当t的值为10-5或10+5时,☉D正好经过点B
同课章节目录
