专题(五) 数据的集中趋势和离散程度 专题复习(含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 专题(五) 数据的集中趋势和离散程度 专题复习(含答案) 2025-2026学年数学苏科版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 174.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 16:42:39 | ||
图片预览


文档简介
专题(五) 数据的集中趋势和离散程度
1.
(2024·南充)学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,再按控球技能占60%,投球技能占40%计算选手的综合成绩(百分制).选手小林控球技能得90分,投球技能得80分.小林的综合成绩为 ( )
A. 170分 B. 86分 C. 85分 D. 84分
2. (2023·大庆)某中学积极推进学生综合素质评价改革,该中学学生小明本学期德、智、体、美、劳五项的评价得分如图所示,则小明五项评价得分的众数、中位数、平均数分别为( )
第2题
A. 9分、9分、8.4分
B. 9分、9分、8.6分
C. 8分、8分、8.6分
D. 9分、8分、8.4分
3. 从班上13名排球队员中,挑选7名个头高的参加校排球比赛.若这13名队员的身高各不相同,其中队员小明想知道自己能否入选,则只需知道这13名队员身高数据的 ( )
A. 平均数 B. 中位数 C. 最大值 D. 方差
4. (2024·新疆)某跳远队准备从甲、乙、丙、丁4名运动员中选取1名成绩优异且发挥稳定的运动员参加比赛,他们成绩数据的平均数和方差如下:==5.75,==6.15,==0.02,==0.45,则应选择的运动员是 ( )
A. 甲 B. 乙 C. 丙 D. 丁
5. (2025·常熟期末改编)下表是抽查的某班10名同学中考体育测试成绩统计表.若成绩的平均数为23分,中位数是a分,众数是b分,则a-b的值是 ( )
成绩/分 30 25 20 15
人 数 2 x y 1
A. -5 B. -2.5 C. 2.5 D. 5
6. (2024·大庆)小庆、小铁、小娜、小萌四名同学均从1、2、3、4、5、6这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是 ( )
A. 小庆选出的四个数字的方差等于4.25 B. 小铁选出的四个数字的方差等于2.5
C. 小娜选出的四个数字的平均数等于3.5 D. 小萌选出的四个数字的极差等于4
7. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次测试,因此计算其他39人的平均分为90分,方差为41分2.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是 ( )
A. 平均分不变,方差变大 B. 平均分不变,方差变小
C. 平均分和方差都不变 D. 平均分和方差都改变
8. (1) (2024·广东)数据5、2、5、4、3的众数是 ;
(2) (2024·乐山)一名交警在路口随机监测了5辆过往车辆的速度(单位:千米/时)分别是66、57、71、69、58,那么这5辆车的速度的中位数是 千米/时.
9. (2024·常熟期中)某测试中心分别从操作系统、硬件规格、屏幕尺寸、电池寿命四项对新投入市场的一款智能手机进行测评,四项得分分别为8分、8分、6分、4分.若将上述四项成绩按3∶3∶2∶2的比计算综合成绩,则该手机的综合成绩为 分.
10. 已知3、m、4、n、5这五个数据,其中m、n是方程x2-6x-7=0的两个根,则这组数据的极差为 .
11. (2024·南充)若一组数据6、6、m、7、7、8的众数为7,则这组数据的中位数为 .
12. 小夏计算一组数据的方差时,使用公式s2=[(8-)2+(9-)2+(11-)2+(15-)2+(7-)2],则公式中的值为 .
13. 若一组数据a1、a2、a3的平均数为4,方差为3,则数据a1-2、a2-2、a3-2的平均数为 ,方差为 .
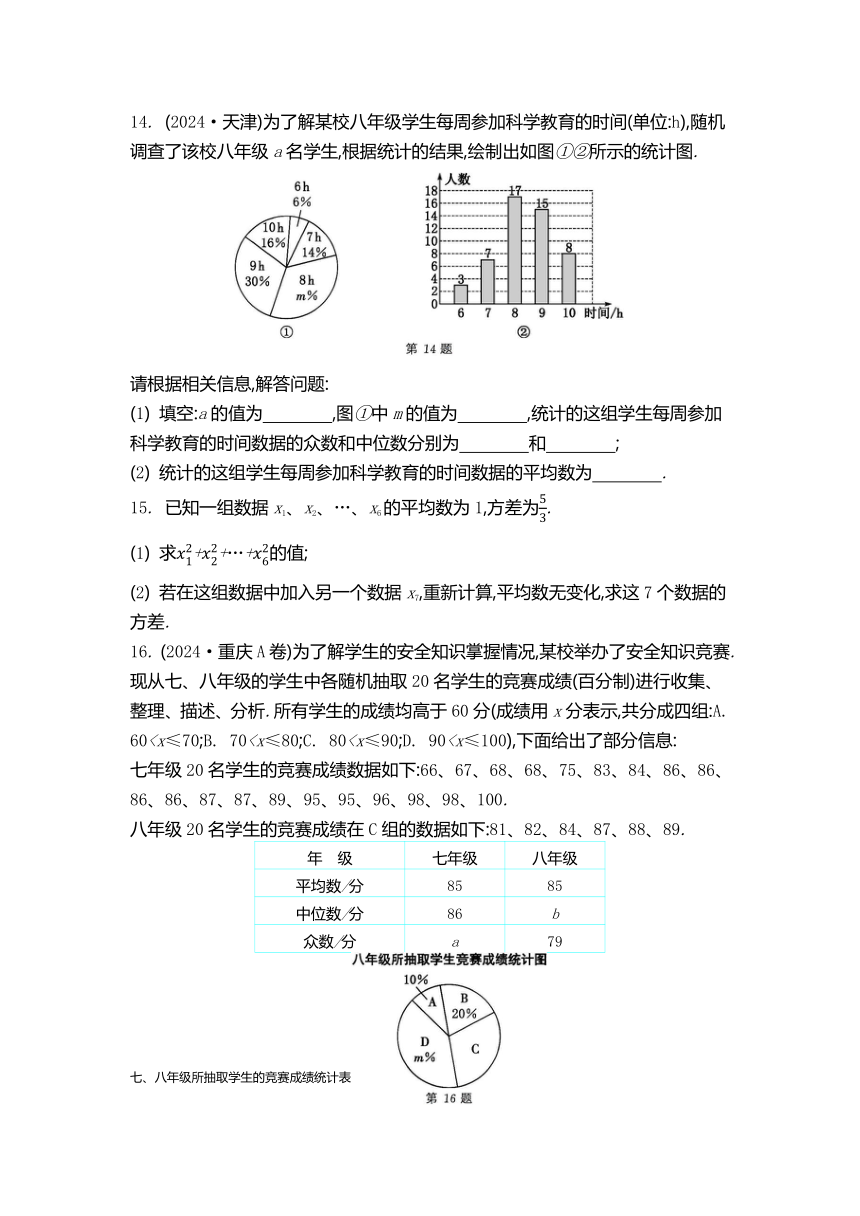
14. (2024·天津)为了解某校八年级学生每周参加科学教育的时间(单位:h),随机调查了该校八年级a名学生,根据统计的结果,绘制出如图①②所示的统计图.
请根据相关信息,解答问题:
(1) 填空:a的值为 ,图①中m的值为 ,统计的这组学生每周参加科学教育的时间数据的众数和中位数分别为 和 ;
(2) 统计的这组学生每周参加科学教育的时间数据的平均数为 .
15. 已知一组数据x1、x2、…、x6的平均数为1,方差为.
(1) 求++…+的值;
(2) 若在这组数据中加入另一个数据x7,重新计算,平均数无变化,求这7个数据的方差.
16. (2024·重庆A卷)为了解学生的安全知识掌握情况,某校举办了安全知识竞赛.现从七、八年级的学生中各随机抽取20名学生的竞赛成绩(百分制)进行收集、整理、描述、分析.所有学生的成绩均高于60分(成绩用x分表示,共分成四组:A. 60七年级20名学生的竞赛成绩数据如下:66、67、68、68、75、83、84、86、86、86、86、87、87、89、95、95、96、98、98、100.
八年级20名学生的竞赛成绩在C组的数据如下:81、82、84、87、88、89.
年 级 七年级 八年级
平均数/分 85 85
中位数/分 86 b
众数/分 a 79
根据以上信息,解答下列问题:
(1) 上述图表中a= ,b= ,m= .
(2) 根据以上数据分析,你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好 请说明理由(写出一条理由即可).
(3) 该校七年级有400名学生、八年级有500名学生参加了此次安全知识竞赛,估计该校七、八年级参加此次安全知识竞赛的成绩优秀(9017. 为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两人在相同条件下各射击10次,为了比较两人的成绩,制作了如下统计表和如图所示的统计图.
甲、乙射击成绩统计表
运动员 平均数/环 中位数/环 方差/环2 命中10环的次数
甲 7 0
乙 1
(1) 请补全折线统计图,并填表.
(2) 如果规定成绩较稳定者胜出,你认为谁胜出 请说明理由.
(3) 如果希望(2)中的另一名选手胜出,那么应该制定怎样的评判规则 为什么
专题(五) 数据的集中趋势
和离散程度
1. B 2. B 3. B 4. C
5. C 解析:由题意,得即解得由此可以求出a=22.5,b=20,∴ a-b=2.5.
6. A 7. B 8. (1) 5 (2) 66 9. 6.8 10. 8 11. 7
12. 10 解析:=×(8+9+11+15+7)=10.
13. 2 3 14. (1) 50 34 8 8 (2) 8.36
15. (1) ∵ 数据x1、x2、…、x6的平均数为1,∴ x1+x2+…+x6=1×6=6.又∵ 这组数据的方差为,∴ (x1-1)2+(x2-1)2+…+(x6-1)2=×6.整理,得++…+-2(x1+x2+…+x6)+6=10,即++…+-2×6+6=10.∴ ++…+=16 (2) ∵ 数据x1、x2、…、x7的平均数为1,∴ x1+x2+…+x7=1×7=7,∴ 6+x7=7,∴ x7=1,∴ 这7个数据的方差为×[(x1-1)2+(x2-1)2+…+(x6-1)2+(x7-1)2]=×[10+(1-1)2]=
16. (1) 86 87.5 40 解析:在七年级20名学生的竞赛成绩中86分出现的次数最多,故a=86;把八年级20名学生的竞赛成绩数据从小到大排列,排在中间的两个数分别是87、88,故b==87.5;由m%=1-10%-20%-=40%,得m=40.
(2) 八年级学生的安全知识竞赛成绩较好 理由:∵ 两个年级成绩的平均数相同,但八年级的中位数高于七年级,∴ 八年级学生的安全知识竞赛成绩较好(答案不唯一).
(3) 400×+500×40%=120+200=320(人).答:估计该校七、八年级参加此次安全知识竞赛的成绩优秀(9017. (1) 补全统计表如表所示,补全折线统计图如图所示
(2) 甲 理由:∵ 甲、乙两人的平均成绩相同,甲的方差小于乙的方差,即甲的成绩较稳定,∴ 甲胜出. (3) 答案不唯一,如应该制定的评判规则如下:平均成绩高的胜出;如果平均成绩相同,那么随着比赛的进行,发挥越来越好者或命中10环的次数多者胜出 ∵ 甲、乙的平均成绩相同,乙只有第5次射击比第4次射击少命中1环,且命中1次10环,而甲第2次比第1次、第4次比第3次、第5次比第4次、第9次比第8次命中的环数都低,且命中10环的次数为0,即随着比赛的进行,很有可能乙的射击成绩越来越好,∴ 在此规则下乙胜出
甲、乙射击成绩统计表
运动员 平均数/环 中位数/环 方差/环2 命中10环的 次数
甲 7 7 4 0
乙 7 7.5 5.4 1
1.
(2024·南充)学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,再按控球技能占60%,投球技能占40%计算选手的综合成绩(百分制).选手小林控球技能得90分,投球技能得80分.小林的综合成绩为 ( )
A. 170分 B. 86分 C. 85分 D. 84分
2. (2023·大庆)某中学积极推进学生综合素质评价改革,该中学学生小明本学期德、智、体、美、劳五项的评价得分如图所示,则小明五项评价得分的众数、中位数、平均数分别为( )
第2题
A. 9分、9分、8.4分
B. 9分、9分、8.6分
C. 8分、8分、8.6分
D. 9分、8分、8.4分
3. 从班上13名排球队员中,挑选7名个头高的参加校排球比赛.若这13名队员的身高各不相同,其中队员小明想知道自己能否入选,则只需知道这13名队员身高数据的 ( )
A. 平均数 B. 中位数 C. 最大值 D. 方差
4. (2024·新疆)某跳远队准备从甲、乙、丙、丁4名运动员中选取1名成绩优异且发挥稳定的运动员参加比赛,他们成绩数据的平均数和方差如下:==5.75,==6.15,==0.02,==0.45,则应选择的运动员是 ( )
A. 甲 B. 乙 C. 丙 D. 丁
5. (2025·常熟期末改编)下表是抽查的某班10名同学中考体育测试成绩统计表.若成绩的平均数为23分,中位数是a分,众数是b分,则a-b的值是 ( )
成绩/分 30 25 20 15
人 数 2 x y 1
A. -5 B. -2.5 C. 2.5 D. 5
6. (2024·大庆)小庆、小铁、小娜、小萌四名同学均从1、2、3、4、5、6这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是 ( )
A. 小庆选出的四个数字的方差等于4.25 B. 小铁选出的四个数字的方差等于2.5
C. 小娜选出的四个数字的平均数等于3.5 D. 小萌选出的四个数字的极差等于4
7. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次测试,因此计算其他39人的平均分为90分,方差为41分2.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是 ( )
A. 平均分不变,方差变大 B. 平均分不变,方差变小
C. 平均分和方差都不变 D. 平均分和方差都改变
8. (1) (2024·广东)数据5、2、5、4、3的众数是 ;
(2) (2024·乐山)一名交警在路口随机监测了5辆过往车辆的速度(单位:千米/时)分别是66、57、71、69、58,那么这5辆车的速度的中位数是 千米/时.
9. (2024·常熟期中)某测试中心分别从操作系统、硬件规格、屏幕尺寸、电池寿命四项对新投入市场的一款智能手机进行测评,四项得分分别为8分、8分、6分、4分.若将上述四项成绩按3∶3∶2∶2的比计算综合成绩,则该手机的综合成绩为 分.
10. 已知3、m、4、n、5这五个数据,其中m、n是方程x2-6x-7=0的两个根,则这组数据的极差为 .
11. (2024·南充)若一组数据6、6、m、7、7、8的众数为7,则这组数据的中位数为 .
12. 小夏计算一组数据的方差时,使用公式s2=[(8-)2+(9-)2+(11-)2+(15-)2+(7-)2],则公式中的值为 .
13. 若一组数据a1、a2、a3的平均数为4,方差为3,则数据a1-2、a2-2、a3-2的平均数为 ,方差为 .
14. (2024·天津)为了解某校八年级学生每周参加科学教育的时间(单位:h),随机调查了该校八年级a名学生,根据统计的结果,绘制出如图①②所示的统计图.
请根据相关信息,解答问题:
(1) 填空:a的值为 ,图①中m的值为 ,统计的这组学生每周参加科学教育的时间数据的众数和中位数分别为 和 ;
(2) 统计的这组学生每周参加科学教育的时间数据的平均数为 .
15. 已知一组数据x1、x2、…、x6的平均数为1,方差为.
(1) 求++…+的值;
(2) 若在这组数据中加入另一个数据x7,重新计算,平均数无变化,求这7个数据的方差.
16. (2024·重庆A卷)为了解学生的安全知识掌握情况,某校举办了安全知识竞赛.现从七、八年级的学生中各随机抽取20名学生的竞赛成绩(百分制)进行收集、整理、描述、分析.所有学生的成绩均高于60分(成绩用x分表示,共分成四组:A. 60
八年级20名学生的竞赛成绩在C组的数据如下:81、82、84、87、88、89.
年 级 七年级 八年级
平均数/分 85 85
中位数/分 86 b
众数/分 a 79
根据以上信息,解答下列问题:
(1) 上述图表中a= ,b= ,m= .
(2) 根据以上数据分析,你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好 请说明理由(写出一条理由即可).
(3) 该校七年级有400名学生、八年级有500名学生参加了此次安全知识竞赛,估计该校七、八年级参加此次安全知识竞赛的成绩优秀(90
甲、乙射击成绩统计表
运动员 平均数/环 中位数/环 方差/环2 命中10环的次数
甲 7 0
乙 1
(1) 请补全折线统计图,并填表.
(2) 如果规定成绩较稳定者胜出,你认为谁胜出 请说明理由.
(3) 如果希望(2)中的另一名选手胜出,那么应该制定怎样的评判规则 为什么
专题(五) 数据的集中趋势
和离散程度
1. B 2. B 3. B 4. C
5. C 解析:由题意,得即解得由此可以求出a=22.5,b=20,∴ a-b=2.5.
6. A 7. B 8. (1) 5 (2) 66 9. 6.8 10. 8 11. 7
12. 10 解析:=×(8+9+11+15+7)=10.
13. 2 3 14. (1) 50 34 8 8 (2) 8.36
15. (1) ∵ 数据x1、x2、…、x6的平均数为1,∴ x1+x2+…+x6=1×6=6.又∵ 这组数据的方差为,∴ (x1-1)2+(x2-1)2+…+(x6-1)2=×6.整理,得++…+-2(x1+x2+…+x6)+6=10,即++…+-2×6+6=10.∴ ++…+=16 (2) ∵ 数据x1、x2、…、x7的平均数为1,∴ x1+x2+…+x7=1×7=7,∴ 6+x7=7,∴ x7=1,∴ 这7个数据的方差为×[(x1-1)2+(x2-1)2+…+(x6-1)2+(x7-1)2]=×[10+(1-1)2]=
16. (1) 86 87.5 40 解析:在七年级20名学生的竞赛成绩中86分出现的次数最多,故a=86;把八年级20名学生的竞赛成绩数据从小到大排列,排在中间的两个数分别是87、88,故b==87.5;由m%=1-10%-20%-=40%,得m=40.
(2) 八年级学生的安全知识竞赛成绩较好 理由:∵ 两个年级成绩的平均数相同,但八年级的中位数高于七年级,∴ 八年级学生的安全知识竞赛成绩较好(答案不唯一).
(3) 400×+500×40%=120+200=320(人).答:估计该校七、八年级参加此次安全知识竞赛的成绩优秀(90
(2) 甲 理由:∵ 甲、乙两人的平均成绩相同,甲的方差小于乙的方差,即甲的成绩较稳定,∴ 甲胜出. (3) 答案不唯一,如应该制定的评判规则如下:平均成绩高的胜出;如果平均成绩相同,那么随着比赛的进行,发挥越来越好者或命中10环的次数多者胜出 ∵ 甲、乙的平均成绩相同,乙只有第5次射击比第4次射击少命中1环,且命中1次10环,而甲第2次比第1次、第4次比第3次、第5次比第4次、第9次比第8次命中的环数都低,且命中10环的次数为0,即随着比赛的进行,很有可能乙的射击成绩越来越好,∴ 在此规则下乙胜出
甲、乙射击成绩统计表
运动员 平均数/环 中位数/环 方差/环2 命中10环的 次数
甲 7 7 4 0
乙 7 7.5 5.4 1
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
